A population of sea turtles is growing at a rate of 3% on North Carolina's coast due to great protection
programs on the beaches. If there are currently 3,000 sea turtles, how many years will it take for the
population to double?
Answers
Answer:
23.4 years
Step-by-step explanation:
The exponential growth model is
A = P(1 + r)^5t, where r is the annual growth rate as a decimal fraction.
If the original number (P) is to double, then this model becomes
2P = P(1 + 0.03)^t, or 2 = 1.03^t. Solve this for t by taking the log of both sides:
log 2 = t*log 1.03, or
0.30103
t = --------------- = 23.4 years
0.01284
Related Questions
A window is 12 feet above the ground. A ladder is placed on the ground to reach the window. If the bottom of the ladder is placed 5 feet away from the ladder building, what is the length of the ladder
Answers
Answer:
Therefore, the length of the ladder is 13 feet.
Step-by-step explanation:
This is a classic example of a right triangle problem in geometry. The ladder serves as the hypotenuse of the triangle, while the distance from the building to the ladder and the height of the window serve as the other two sides. Using the Pythagorean theorem, we can solve for the length of the ladder:
ladder^2 = distance^2 + height^2 ladder^2 = 5^2 + 12^2 ladder^2 = 169 ladder = √169 ladder = 13
Therefore, the length of the ladder is 13 feet.
brainliest PLssssss
please help ? i do not understand this question--

Answers
Answer:
hey, i think it's the first alternative
Step-by-step explanation:
This is the second part of a three-part problem. Consider the systom of differential equations
y
1
′
=y
1
+3y
21
y
2
′
=3y
1
+y
2
+
Verify that for any constants c
1
and c
2
, the functions
y
1
(t)=c
1
e
u
+c
2
e
−2t
y
2
(t)=c
1
c
u
−c
2
e
−2t
satisfy the system of differential equations. Enter c
1
as of and c
2
as c2. a. Find the value of each term in the equation y
1
′
=y
1
+3y
2
in terms of the variable f (Enter the terms in the order given.) b. Find the value of each term in the equation y
2
′
=3y
1
+y
2
in terms of the variable f (Enter the terms in the order given.)
Answers
The given system of differential equations is:
y1' = y1 + 3y2
y2' = 3y1 + y2
We need to verify that the functions:
y1(t) = c1e^(ut) + c2e^(-2t)
y2(t) = c1ue^(ut) - c2e^(-2t)
satisfy the system. In part (a), we find the value of each term in the equation y1' = y1 + 3y2 in terms of the variable f. In part (b), we find the value of each term in the equation y2' = 3y1 + y2 in terms of the variable f.
(a) To find the value of each term in y1' = y1 + 3y2, we differentiate y1(t) with respect to t. The derivative of c1e^(ut) is c1ue^(ut), and the derivative of c2e^(-2t) is -2c2e^(-2t). Thus, we have:
y1' = c1ue^(ut) - 2c2e^(-2t) + 3(c1ue^(ut) - c2e^(-2t))
Combining like terms, we get:
y1' = (2c1u + 3c1u)e^(ut) + (-2c2 - 3c2)e^(-2t)
(b) Similarly, we differentiate y2(t) with respect to t. The derivative of c1ue^(ut) is c1u^2e^(ut), and the derivative of c2e^(-2t) is -2c2e^(-2t). Thus, we have:
y2' = c1u^2e^(ut) - 2c2e^(-2t) + 3(c1e^(ut) + c2e^(-2t))
Combining like terms, we get:
y2' = (c1u^2 + 3c1)e^(ut) + (-2c2 + 3c2)e^(-2t)
Therefore, the value of each term in y1' = y1 + 3y2 is given by:
Term 1: (2c1u + 3c1)e^(ut)
Term 2: (-2c2 - 3c2)e^(-2t)
And the value of each term in y2' = 3y1 + y2 is given by:
Term 1: (c1u^2 + 3c1)e^(ut)
Term 2: (-2c2 + 3c2)e^(-2t)
These results verify that the functions y1(t) and y2(t) satisfy the given system of differential equations.
To learn more about derivative click here : brainly.com/question/32963989
#SPJ11
Jaya is the middle of three siblings whose ages are consecutive even integers. If the sum of their ages is 84, find Jaya’s age
Answers
Answer:
26
Step-by-step explanation:
Let jaya's age be a, so consecutive EVEN #s can be written as
a, a+2, a+4
sum = 84 = 3a +6
so 3a = 78
a=26
Freedom PopFreedom PopFreedomFreedom Pop Pop they right?

Answers
Answer:
D
B
Step-by-step explanation:
1. x² - 5x = 14
x² -5x -14 = 0
x² +2x -7x -14 = 0
x(x + 2) -7(x + 2) = 0
x - 7 or x + 2 = 0
x = 7 or x = -2
2. y² + 6y + 9 = 49
y² + 6y +9 -49 = 0
y² +6y -40 = 0
y² +10y -4y -40 = 0
y(y + 10) -4(y + 10) = 0
y -4 or y + 10 = 0
y = 4 or y = -10
Identify the segments that are parallel, if any, if FDC = GCH
A. AC||CD
B. AD||CB
C. BA||CA
D. AE||CB

Answers
Answer:
B
Step-by-step explanation:
The two lines will never intersect regardless of the distance they go
Answer:
B. AD parallel CB
Step-by-step explanation:
If angles F D C = G C H, that makes them corresponding angles.
The transversal being EH, so AD must be parallel to BC, or
alternatively, AD parallel CB.
What must be the value of c , if the following is to be a probability density function? Round your answer to two decimal places.
{c(5x − 4 − x2)0if 1 ≤ x ⩽ 4otherwise Numeric Response
Answers
The value of c that makes the given function a probability density function is 3/2.
A probability density function is a function that describes the likelihood of a random variable taking on a specific value within a given range.
In order for a function to be a probability density function, it must satisfy certain conditions, such as being non-negative and integrating to 1 over its domain.
In this problem, we are given a function:
c(5x - 4 - x²)if 1 ≤ x ≤ 4, and 0 otherwise.
We need to find the value of c that will make this function a probability density function. That means we need to check whether the function is non-negative and integrates to 1 over the interval [1, 4].
First, let's check whether the function is non-negative. Since c is a constant, we just need to look at the expression inside the parentheses.
For this expression to be non-negative, we need to find its roots:5x - 4 - x² = 0⇒ x² - 5x + 4 = 0⇒ (x - 1)(x - 4) = 0The roots are x = 1 and x = 4.
We can see that the expression inside the parentheses is negative between these two roots, and positive outside this interval.
Therefore, the function is only non-negative for values of x between 1 and 4.Next, let's check whether the function integrates to 1 over the interval [1, 4].
We can do this by evaluating the integral:
integral(1, 4, c(5x - 4 - x²)) = 1
We can simplify this expression by pulling the constant c outside the integral and then integrating the expression inside the parentheses:
integral(1, 4, 5x - 4 - x²) = 1
Using the power rule of integration, we get:
[(5/2)x² - 4x - (1/3)x³]1⁴ = 1
Simplifying this expression, we get:
(5/2)(4²) - 4(4) - (1/3)(4³) - (5/2)(1²) + 4(1) + (1/3)(1³) = 1
Solving for c, we get:
c = 3/2
So the value of c that makes the given function a probability density function is 3/2.
For more such questions on probability, click on:
https://brainly.com/question/30390037
#SPJ8
Convert 124 into Binary number
Convert 0 1 1 1 0 1 1 1 into decimal number
Find the value of following calculation in Binary Value
1 0 1 1 1
+ 1 1 0 0 1
+ 0 1 1 1 0
Answers
1.The decimal number 124 is equivalent to the binary number 1111100. 2.The binary number 01110111 is equivalent to the decimal number 119. 3.The binary calculation of 10111 + 11001 + 01110 equals 111010.
1.To convert the decimal number 124 into binary, we divide the number by 2 repeatedly until the quotient becomes 0. The remainders obtained from each division form the binary digits, with the last remainder being the least significant digit. Therefore, 124 in binary is 1111100.
2.To convert the binary number 01110111 into decimal, we multiply each digit by the corresponding power of 2 and sum the results. The leftmost digit has a power of 2 equal to the number of digits minus 1. Thus, 0 x 2^7 + 1 x 2^6 + 1 x 2^5 + 1 x 2^4 + 0 x 2^3 + 1 x 2^2 + 1 x 2^1 + 1 x 2^0 equals 119 in decimal.
3.To perform the binary calculation 10111 + 11001 + 01110, we add each corresponding bit from right to left, carrying over any excess from the previous addition. The result is 111010, which is the binary representation of the sum of the three numbers.
Learn more about decimal number here:
https://brainly.com/question/4708407
#SPJ11
Solve: -2(2x+6)= -3x
Answers
hope you find this helpful. :D

Answer:
below
Step-by-step explanation:
-2(2x+6)=-3x
1. distribute
-4x-12=-3x
2. add 3x to both sides
-x-12=0
3. add 12 to both sides
-x = 12
4. divide both sides by -x or -1
-x/-1 = 12/-1
ANSWER : x = -12
9-12x+6y apply the distributive property to factor out the greatest common factor of all three terms
Answers
To factor out the greatest common factor of the expression 9-12x+6y, we need to identify the greatest common factor of all three terms. The numbers 9, 12, and 6 have a common factor of 3, and the variables x and y have no common factors. Therefore, we can factor out 3 from each term using the distributive property.
9-12x+6y = 3(3-4x+2y)
This is the fully factored form of the expression, and we can see that the greatest common factor of all three terms is 3. By factoring out the greatest common factor, we simplify the expression and make it easier to work with.
To apply the distributive property and factor out the greatest common factor (GCF) of the terms in the expression 9 - 12x + 6y, follow these steps:
1. Identify the GCF of the coefficients (9, -12, and 6). The GCF is 3.
2. Factor out the GCF from each term: 3(3 - 4x + 2y).
3. The factored expression is now 3(3 - 4x + 2y).
By applying the distributive property and factoring out the GCF, we simplified the expression to its factored form, making it easier to work with in further calculations.
Learn more about distributive property here: brainly.com/question/32019808
#SPJ11
I need help with this polynomial question: (5x^5-2x)-(4x^4+3x^2). This ^ means to the power of.
Answers
Answer:
Step-by-step explanation:
5x^5 - 2x - 4x^4 - 3x^2
5x^5 - 4x^4 - 3x^2 - 2x
-3(8+j)=-16+5j
HELP ASAP NEED THIS DONE TONIGHT BEFORE MIDNIGHT
Answers
Answer:
j = -1
Step-by-step explanation:
Eliminate parentheses:
-24 -3j = -16 +5j
Add 3j+16
-8 = 8j
Divide by the coefficient of j.
-1 = j
\(\rm⇢ \: \: - 3(8 + j) = - 16 + 5j\)
\(\rm⇢ \: \: - 24 - 3j = - 16 + 5j\)
\(\rm⇢ \: \: 5j + 3j = - 24 + 16\)
\(\rm⇢ \: \: 8j = - 8\)
\(\rm⇢ \: \: j = - 1\)
Toilet rolls come in packs of 4 and 9
The 4-pack is £2.04
The 9-pack is £4.68
By calculating the price per roll, determine which pack is better value.
Answers
Answer:
Buy 8 pack with £2.04 and buy 1 pack with £0.52 will be more value
Step-by-step explanation:
To calculate 1 roll:
2.04/4= £0.51
4.68/9= £0.52
(0.51+0.52)/2= £0.515 = £0.52 per roll
which pack is better value:
2.04 (4 pack) x2= £4.08 for 8 pack
4.08+0.52= £4.6 for 9 pack
£4.6<£4.68
Therefore, buy 8 pack with £2.04 and buy 1 pack with £0.52 will be more value.
What is the equation of a line, in point-slope form, that passes through (-8, 1) and has a slope of 5/6?
Answers
Answer:
y-1=\(\frac{5}{6}\)(x+8)
Step-by-step explanation:
1. y-y1=m(x-x1) (point slope form)
2. y1 is the y of your given point and x1 is the x of your given point
3. m is the slope
29 out of 50 people interviewed said they liked orange juice with their breakfast what percent of those interviewed said they like orange juice for breakfast
Answers
The percent of those interviewed said they like orange juice for breakfast is 58%.
What is a percentage?A percentage is a number or ratio that can be expressed as a fraction of 100 in mathematics. If we need to calculate the percentage of a number, divide it by the whole and multiply by 100. As a result, the percentage denotes a part per hundred. The term % refers to one hundred percent.
The percent of those interviewed said they like orange juice for breakfast will be:
= Orange juice taker / Total respondent
= 29/50
= 0.58
= 58%
Read more about percentage
brainly.com/question/24877689
#SPJ1
The sales of oven mitts and thermometers at a store are related by the equation 0.1x^3 + 7xy + 7.7y^3 = 55791.5, where x is the number of oven mitts and y is the number of thermometers sold. Step 2 of 2: Find dy/dx if x = 18 and y = 19. Enter the exact answer or round to the nearest thousandth. dy/dx |(x,y)=(18,19) ____________
Answers
Answer: dy/dx|(x,y)=(18,19)
= -0.0275
The given equation is:
0.1x³ + 7xy + 7.7y³
= 55791.5
To find: Find dy/dx if
x = 18 and
y = 19.
Solution:Given, the equation: 0.1x³ + 7xy + 7.7y³
= 55791.5
We have to find the value of dy/dx when x = 18 and
y = 19.
Therefore, differentiating both sides with respect to x and using the Chain Rule, we get:
0.3x² + 7y dx/dx + 7x dy/dx + 23.1y² dy/dx
= 0
Now, we have to find the value of dy/dx when x = 18 and
y = 19.
At (18, 19), we get: 0.3(18)² + 7(19) (1) + 7(18) dy/dx + 23.1(19)² dy/dx
= 0⇒ 97.2 + 133 + 126 dy/dx + 8231.1 dy/dx
= 0⇒ 8359.1 dy/dx
= −230.2⇒ dy/dx
= −230.2 / 8359.1≈ −0.0275
Therefore, the value of dy/dx when x = 18 and y = 19 is approximately -0.0275.
To know more about oven visit;
brainly.com/question/29486074
#SPJ11
If y = -5, what is the value of
2y+2
-
4
Answers
Answer:
-12
Step-by-step explanation:
Ok so I'm guessing that's a -4 but if its not, please correct me.
y= -5 is going to be plugged into 2y+2-4
This means that 2(-5)+2-4=?
2(-5) is the equivalent to 2 times -5, which is -10 (you solve multiplication first because order of operations)
Now, 2-4=-2
So using this, let's combine both equations!
-10+-2=?
?=-12
It's a lot of steps but they get easier the more you do them <3
Use the simple interest formula to find the ending balance
$2,500 at 5.9% for 7 years
Answers
The ending balance is $1032.5.
What is simple interest?
Simple interest is an interest rate that is solely calculated on the principal amount or the portion of the principal that is still owed. It does not take compounding into account. Simple interest may be used on a schedule other than annually, such as every month, week, or even every day.
Here, we have
Given: P = $2,500, r = 5.9%, t = 7 years
Convert 5.9% to a decimal
5.9% = 5.9 ÷ 100
= 0.059
Substitute the values into the simple interest formula,
I = Prt and we get
I = Prt
= 2500 × 0.059 × 7
= $1032.5
Hence, the ending balance is $1032.5.
To learn more about the simple interest from the given link
https://brainly.com/question/25793394
#SPJ1
i need help with #5!! the sum is 4.5 but i don’t know a, y,
B, or d. PLZ ANSWERRR.
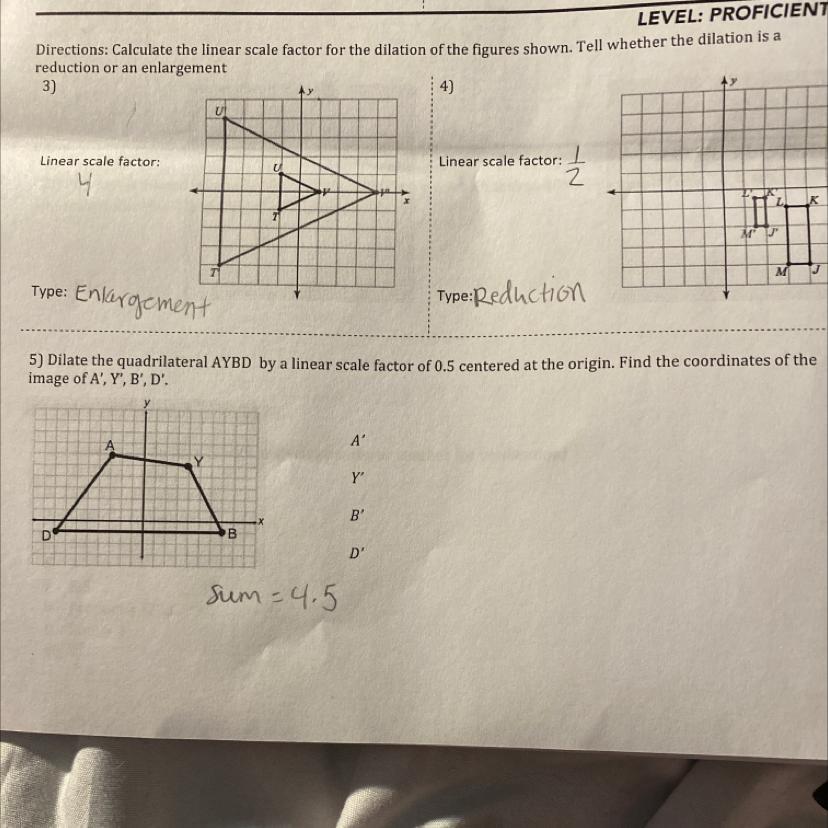
Answers
Answer:
A is -4, 6
Y is 4, 5
B is 7, -1
D is -8, -1
what is the domain and range

Answers
Answer:
0,1,2,3 is the domain
-2,1,2,4 is the range
The standard length of a piece of cloth for a bridal gown is 3.25 meters. A customer selected 35 pcs of cloth for this purpose. A mean of 3.52 meters was obtained with a variance of 0.27 m2 . Are these pieces of cloth beyond the standard at 0.05 level of significance? Assume the lengths are approximately normally distributed
Answers
The pieces of cloth are beyond the standard at 0.05 level of significance.
We can use a one-sample t-test to determine if the mean length of the 35 pieces of cloth is significantly different from the standard length of 3.25 meters.
The null hypothesis is that the mean length of the cloth pieces is equal to the standard length:
H0: μ = 3.25
The alternative hypothesis is that the mean length of the cloth pieces is greater than the standard length:
Ha: μ > 3.25
We can calculate the test statistic as:
t = (x - μ) / (s / √n)
where x is the sample mean length, μ is the population mean length (3.25 meters), s is the sample standard deviation (0.52 meters), and n is the sample size (35).
Plugging in the values, we get:
t = (3.52 - 3.25) / (0.52 / √35) = 3.81
Using a t-table with 34 degrees of freedom (n-1), and a significance level of 0.05 (one-tailed test), the critical t-value is 1.690.
Since our calculated t-value (3.81) is greater than the critical t-value (1.690), we reject the null hypothesis and conclude that the mean length of the 35 pieces of cloth is significantly greater than the standard length at the 0.05 level of significance.
Know more about level of significance here:
https://brainly.com/question/30542688
#SPJ11
define nature
have a great day
Answers
Answer:
Nature : The phenomena of the physical world collectively, including plants, animals, the landscape, and other features and products of the earth, as opposed to humans or human creations. (according to Oxford Dictionary)
Anyone watch anime? If you do plz answer lol, have a good day :)
Answers
Answer:
MYSTREET AND MY INNER DEMONS YES
Step-by-step explanation:
watch them
1) Find the remainder when 4x3 - 5x2 + 2x - 14 is divided by x -2
with the help of remainder theorem.
{ANS: R=2}
Answers
Answer:
remainder = 2
Step-by-step explanation:
A polynomial f(x) is divided by (x - a) then the remainder is f(a)
Here f(x) = 4x³ - 5x² + 2x - 14 is divided by (x - 2) then remainder is f(2)
f(2) = 4(2)³ - 5(2)² + 2(2) - 14
= 4(8) - 5(4) + 4 - 14
= 32 - 20 - 10
= 12 - 10
= 2
the amount of gold produced (in troy ounces) during the california gold rush from 1848 to 1888 can be modeled by G(t) = 25t / t^2+ 16 where t is the number of years since 1848 and 0≤t≤40. Part a) Use the closed interval method to determine the absolute maximum amount of gold produced during the California gold rush. Also, state the year when the absolute maximum production was achieved. Part a) Use the closed interval method to determine the absolute minimum amount of gold produced during the California gold rush. Also, state the year when the absolute minimum production was achieved.
Answers
The absolute minimum amount of gold produced during the California gold rush was at t = 40 years (1888), with a production of G(40) ≈ 0.195 troy ounces.
What are derivatives?A function's varied rate of change with respect to an independent variable is referred to as a derivative. When there is a variable quantity and the rate of change is irregular, the derivative is most frequently utilised.
To find the absolute maximum and minimum values of G(t) on the closed interval [0, 40], we need to first find the critical points and endpoints of G(t) on this interval.
Taking the derivative of G(t), we have:
G'(t) = (25(t² + 16) - 25t(2t))/ (t² + 16)²
= 25(16 - t²) / (t² + 16)²
Setting G'(t) equal to zero, we get:
25(16 - t²) / (t² + 16)² = 0
Simplifying this expression, we have:
16 - t² = 0
This gives us t = ±4.
However, we need to check whether these critical points are actually maximum or minimum points, or neither.
We can do this by using the first derivative test, which involves checking the sign of G'(t) on either side of the critical points.
For t < -4, G'(t) < 0, indicating that G(t) is decreasing.
For -4 < t < 4, G'(t) > 0, indicating that G(t) is increasing.
For t > 4, G'(t) < 0, indicating that G(t) is decreasing.
Therefore, we can conclude that t = -4 is a local maximum point, and t = 4 is a local minimum point.
Next, we need to check the endpoints of the interval [0, 40].
At t = 0, G(0) = 0.
At t = 40, G(40) = 25(40) / (40² + 16) ≈ 0.195 troy ounces.
Comparing all of these values, we can see that the absolute maximum amount of gold produced during the California gold rush was at t = 4 years (1852), with a production of G(4) ≈ 1.562 troy ounces.
The absolute minimum amount of gold produced during the California gold rush was at t = 40 years (1888), with a production of G(40) ≈ 0.195 troy ounces.
Learn more about derivatives on:
https://brainly.com/question/23819325
#SPJ4
DeepSea Challenger’s descent was a change in depth of (-4) feet per second.We can use the equation y = -4x to model this relationship, where y is the depth (-35,814 ft) and x is the time in seconds that have passed. How many seconds does this model suggest it would take for DeepSea Challenger to reach the bottom?(round to the nearest tenth)
* Explain how you got your answer.
Answers
Answer:
Step-by-step explanation:
x = -35,814 ft ⋅ (1 sec)/(-4 ft) = 8,953.5 sec
The required model suggests that it would take approximately 8957.5 seconds for DeepSea Challenger to reach the bottom.
What is proportionality?proportionality is defined as between two or more sets of values, and how these values are related to each other in the sense are they directly proportional or inversely proportional to each other.
To find the time it takes for the DeepSea Challenger to reach the bottom, we need to find the value of x when y = -35,814 ft.
We can substitute the desired depth into the equation y = -4x:
-35,814 = -4x
35,814 = 4x
x = 35,814 / 4
x = 8953.5 seconds
So, the model suggests that it would take approximately 8957.5 seconds for DeepSea Challenger to reach the bottom.
Learn more about proportionality here: https://brainly.com/question/22620356
#SPJ5
Deshaun is fertilizing his garden. The garden is in the shape of a rectangle. Its length is 14 feet and its width is 11 feet. Suppose each bag of fertilizer covers 22 square feet. How many bags will he need to cover the garden?
Answers
Answer:
length x width = area
14 x 11 = 154
154 / 22 = 7 fertilizer needed
Hope this helps
Step-by-step explanation:
Giving brainliest
Determine the current temperature in degrees Fahrenheit if the current temperature is 32 degrees Celsius in Lima, Peru. Round the final answer to the nearest whole number.
32
56
90
103
Answers
Answer:
The answer is 90.
Thank you
Answer:
89.6
Step-by-step explanation:
The formula to convert Celsius to Fahrenheit is given by °F = °C × (9/5) + 32
F = [ C × (9/5) + 32 ]
Given that, C = 32
F = 32 × (9/5) + 32
F = 32 [ 1 + (9/5) ]
F = 32 [ 1 + 1.8 ]
F = 32 × 2.8
F = 89.6
With Alpha set to .05, would we reduce the probability of a Type
I Error by increasing our sample size? Why or why not? How does
increasing sample size affect the probability of Type II Error?
Answers
With Alpha set to .05, increasing the sample size would not directly reduce the probability of a Type I error. The probability of a Type I error is determined by the significance level (Alpha) and remains constant regardless of the sample size.
However, increasing the sample size can indirectly affect the probability of a Type I error by increasing the statistical power of the test. With a larger sample size, it becomes easier to detect a statistically significant difference between groups, reducing the likelihood of falsely rejecting the null hypothesis (Type I error).
Increasing the sample size generally decreases the probability of a Type II error, which is failing to reject a false null hypothesis. With a larger sample size, the test becomes more sensitive and has a higher likelihood of detecting a true effect if one exists, reducing the likelihood of a Type II error. However, it's important to note that other factors such as the effect size, variability, and statistical power also play a role in determining the probability of a Type II error.
Learn more about Alpha here:
https://brainly.com/question/30447633
#SPJ11
if the population is symmetric but not perfectly normal, the sampling distribution of sample mean will be
Answers
The sampling distribution of the sample mean will be approximately normal due to the central limit theorem, even if the population is symmetric but not perfectly normal.
If the population is symmetric but not perfectly normal, the sampling distribution of the sample mean will still be approximately normal due to the central limit theorem. The central limit theorem states that regardless of the shape of the population distribution, as long as the sample size is sufficiently large (typically n > 30), the distribution of the sample mean will tend to be approximately normal.
This is because the sample mean is an average of individual observations, and the averaging process tends to smooth out any deviations from normality in the population. Therefore, even if the population is not perfectly normal, the sampling distribution of the sample mean will approach a normal distribution as the sample size increases.
To learn more about sampling distribution click here brainly.com/question/29375938
#SPJ11