A phone company offers two monthly plans. Plan A costs $20 plus an additional $0.07 for each minute of calls. Plan B costs $16 plus an additional $0.11 for each minute of calls.
Question A) For what amount of calling do the two plans cost the same?
Question B)What is the cost when the two plans cost the same?
Answers
Related Questions
Find an equation for the surface obtained by rotating the line x = 4y about the x-axis.
Answers
The equation: \(\frac{x^{2}}{6^{2}}={y^{2}+z^{2}\), represents a circle with radius r = y = x/6, and the surface that results is a cone, as obtained with the help of surface of revolution.
What is surface of revolution?A surface created by rotating a two-dimensional curve about an axis is known as a surface of revolution. As a result, the final surface is always symmetric along the azimuth.Now,
If we consider the point (6y, y, 0) in the xy plane, it appears to be a circular path that is a cone when the curve is rotated about the x axis. The cone's equation takes the following form:
\(\frac{x^{2}}{c^{2}}=\frac{y^{2}}{a^{2}}+\frac{z^{2}}{b^{2}}\)
Given that x = 6y, we square x = 6y to give the equation the form shown above, which results in:
x² = (6y)²
x² = 36y²
Circular paths go parallel to the y-axis, hence the equation should be circular in nature. 36z² needs to be added, so:
x² = 36y² + 36z²
=> \(\frac{x^{2}}{6^{2}}={y^{2}+z^{2}\)
Hence, This equation represents a circle with radius r = y = x/6, and the surface that results is a cone, as obtained with the help of surface of revolution.
To learn more about Surface of revolution, refer to the link: https://brainly.com/question/14640419
#SPJ4
If a driver drives at a constant rate of 32 miles per hour, how long would it take the driver to drive 323 miles?
Answers
Answer:
About 10 hours
Step-by-step explanation:
Pass through (-6,-6) parallel to y= 4/3x+8
Answers
Answer:
y
=
4
3
x
−
6
Step-by-step explanation:
The equation of the line is y = ( 4/3 )x + 2.
What is an equation of a line?An equation of the line is defined as a linear equation having a degree of one. The equation of the line contains two variables x and y. And the third parameter is the slope of the line which represents the elevation of the line.
Given that the equation is parallel the line y = ( 4 / 3 )x + 8 and passes through the point ( -6 , -6 ).
The general equation of the line is
y = mx + c
The slope of the required line will be the same as the slope of the line parallel to the required line.
m = ( 4 / 3 )
The equation of the line will be written:-
y = mx + c
y = ( 4 / 3 )x + c
-6 = ( 4 / 3 ) x -6 + c
c = 2
y = ( 4/3 )x + 2
Therefore, the equation of the line is y = ( 4/3 )x + 2.
To know more about an equation of the line follow
brainly.com/question/18831322
#SPJ2
The table below gives beverage preferences for random samples of teens and adults. Teens Adults Total Coffee 50 200 250 Tea 100 150 250 Soft Drink 200 200 400 Other 50 50 100 400 600 1000 We are asked to test for independence between age (i.e., adult and teen) and drink preferences. The expected number of adults who prefer coffee is a. 150. b. 200. c. .25. d. .33.
Answers
The expected number of adults who prefer coffee is 150.
We must determine the anticipated number of adults who prefer coffee in order to test for independence between age and drink preferences.
First, let's look at the totals of the rows and columns to figure out the expected values for each category. The formula is available to us:
Anticipated esteem = (Line absolute * Section complete)/Stupendous aggregate
The stupendous complete for this situation is 1000.
Number of adults expected to prefer coffee:
= (Adults total minus Coffee total) / Grand total = (600 minus 250) / 1000 = 150; consequently, 150 adults are anticipated to prefer coffee.
In this way, the right response is (a) 150.
To know more about Number, visit
brainly.com/question/24644930
#SPJ11
GIVING BRAINLIEST IF CORRECT!! EASY MATH!!!
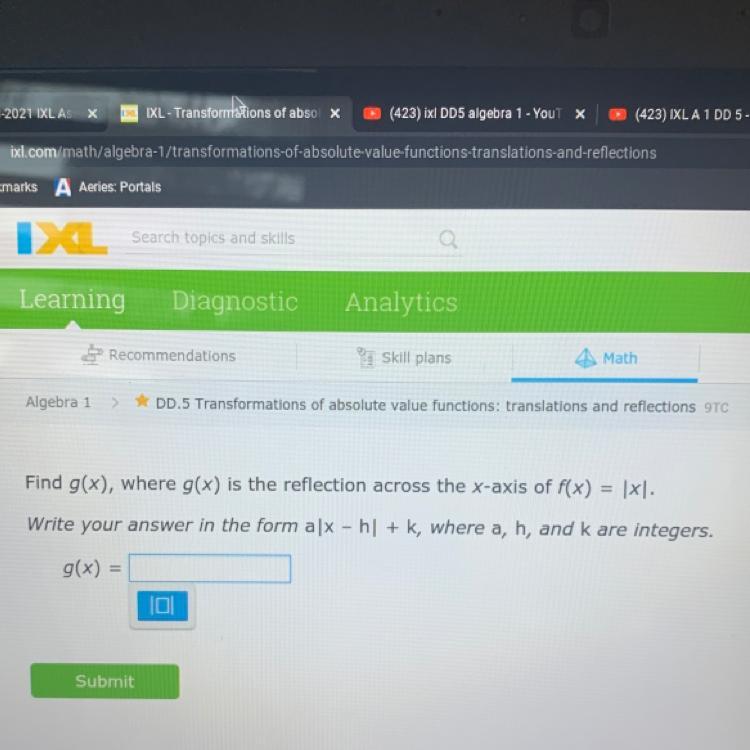
Answers
Answer:
Reflecting across the x-axis looks like this: -g(x)
A negative on the outside of the function.
So your answer may be
-|x|
help me out and please provide steps

Answers
Answer:
3(x+2)/(2(x+4))
Step-by-step explanation:
A compound fraction is simplified by rewriting it as a simple fraction, and reducing it to lowest terms by cancelling common factors from numerator and denominator. The division of one fraction by another is accomplished in the usual way: multiply the numerator by the inverse of the denominator.
__
\(\dfrac{\left(\dfrac{6x^2-24}{x^2+7x+12}\right)}{\left(\dfrac{4x^2-4x-8}{x^2+4x+3}\right)}=\left(\dfrac{6x^2-24}{x^2+7x+12}\right)\times\left(\dfrac{x^2+4x+3}{4x^2-4x-8}\right)\\\\=\dfrac{6(x-2)(x+2)}{(x+3)(x+4)}\times\dfrac{(x+1)(x+3)}{4(x-2)(x+1)}=\dfrac{3(x-2)(x+1)(x+2)(x+3)}{2(x-2)(x+1)(x+3)(x+4)}\\\\=\boxed{\dfrac{3(x+2)}{2(x+4)}}\)
Please help me now! :c

Answers
Answer:
1/64
Step-by-step explanation:
(1/8)² = 1/64
Triangle RAD is reflected over the x-axis to form triangleR'A'D' (not shown). Then triangle R'A'D'is
translated to form triangle R" A"D"(not shown). Point A" is shown plotted on the xy-plane after the second
transformation. Determine the coordinates of D"?
OD" (7,2)
O D" (9,-10)
OD" (4,-2)
OD" (7-10).
Answers
Answer:
(7,-10)
Very educated guess
The perimeter of a rectangle is 22cm and the length of each side is a natural number. How many different areas in centimeter squared can the rectangle have?
Answers
option B is the correct answer.
The perimeter of a rectangle is 22 cmLet the length of the rectangle be 'l' and the breadth be 'b'As per the question, the perimeter of the rectangle is given by;Perimeter = 2(l + b) => 2(l + b) = 22 => l + b = 11.As we know that the area of a rectangle is given by;Area = l × b
Therefore, the different areas of the rectangle are; l × b1 × (11 - 1) = 10 cm²2 × (11 - 2) = 18 cm²3 × (11 - 3) = 24 cm²4 × (11 - 4) = 28 cm²5 × (11 - 5) = 30 cm²6 × (11 - 6) = 30 cm²7 × (11 - 7) = 28 cm²8 × (11 - 8) = 24 cm²9 × (11 - 9) = 18 cm²10 × (11 - 10) = 10 cm²Hence, there are only 8 different areas of the rectangle i.e., 10 cm², 18 cm², 24 cm², 28 cm², 30 cm².
To know more about Perimeter visit:
https://brainly.com/question/7486523
#SPJ11
1. What is the vertex of f(x) = 3(x + 2)^2 - 4?
2. Does this function have a maximum or minimum value? f(x) = (x - 4)^2 +3?

Answers
Answer:
3) A. (-2, - 4);4) B. Minimum.----------------------------
Question 3The vertex form of a parabola is:
f(x) = a(x - h)² + k, where a - leading coefficient, (h, k) - the vertexGiven equation is:
f(x) = 3(x + 2)² - 4Hence h = - 2, k = - 4, therefore its vertex is (- 2, - 4).
Question 4When a > 0, the graph opens up, it means the function has a minimum but no maximum value;When a < 0, the graph opens down, it means the function has a maximum but no minimum value.Given function:
f(x) = (x - 4)² + 3,It has a = 1, hence the graph opens up, therefore the function has a minimum.
A cattle rancher gave 1/3 of his land to his son and kept the remaining 2/3 for himself. He kept 34 acres of land. How much land did he have to begin with?(explain with detail and steps please I do not just want the answar thank you)
Answers
Answer:
He had 51 acres to start with.
Step-by-step explanation:
Let the original plot of land be x
2/3 x = 34 Multiply both sides by 3
3 * 2/3 x = 34 * 3
2x = 102 Divide by 2
2x/2 = 102/2
x = 51
Answer:
51 Acres of land
Step-by-step explanation:
A curve is described by the parametric equations x = t^2 + 2t and y = t^3 + t^2. An equation of the line tangent to the curve at the point determined by t = 1 is...?
Answers
To find the equation of the tangent line, we need to find the derivative of both x and y with respect to t and evaluate them at t = 1 to get the slope of the tangent line. The equation of the line tangent to the curve at the point determined by t = 1 is y = (5/4)(x - 3) + 2.
dx/dt = 2t + 2
dy/dt = 3t^2 + 2t
At t = 1, dx/dt = 4 and dy/dt = 5
So the slope of the tangent line is m = dy/dx = (dy/dt)/(dx/dt) = 5/4
Now we need to find the point on the curve where t = 1.
x = t^2 + 2t = 1^2 + 2(1) = 3
y = t^3 + t^2 = 1^3 + 1^2 = 2
Therefore, the point on the curve where t = 1 is (3, 2)
Using the point-slope form of a line, we can write the equation of the tangent line as:
y - 2 = (5/4)(x - 3)
Simplifying:
y = (5/4)x - (7/2)
So the equation of the line tangent to the curve at the point determined by t = 1 is y = (5/4)x - (7/2).
A curve is described by the parametric equations x = t^2 + 2t and y = t^3 + t^2. An equation of the line tangent to the curve at the point determined by t = 1 is given by the formula y = m(x - x1) + y1, where m is the slope, and (x1, y1) is the point of tangency.
First, find the point of tangency (x1, y1) by plugging t = 1 into the parametric equations:
x1 = (1)^2 + 2(1) = 3
y1 = (1)^3 + (1)^2 = 2
Next, find the derivatives of x and y with respect to t:
dx/dt = 2t + 2
dy/dt = 3t^2 + 2t
Now, find the slope m by dividing dy/dt by dx/dt at t = 1:
m = (dy/dt) / (dx/dt) = (3(1)^2 + 2(1)) / (2(1) + 2) = (5/4)
Finally, plug the slope m and point (x1, y1) into the equation of the tangent line:
y = (5/4)(x - 3) + 2
So, the equation of the line tangent to the curve at the point determined by t = 1 is y = (5/4)(x - 3) + 2.
Learn more about tangent line at: brainly.com/question/23416900
#SPJ11
I need help!!!!!!!!!!!!!!1

Answers
Answer:
∠2 = 125°
Step-by-step explanation:
∠1 and ∠2 form a straight angle of 180° (∠3 and ∠4 aswell)
∠1 = ∠3, because they are cross angles (∠3 and ∠4 aswell)
We can write an equation according to this and find y:
(8y - 9)° = (6y + 7)°
8y - 6y = 7 + 9
2y = 16 / : 2
y = 8
∠1 = 8 × 8 - 9 = 55°
∠2 = 180° - 55° = 125°
∠3 =∠1 = 6 × 8 + 7 = 55°
∠4 = 180° - 55° = 125°
The diagonals of kite KITE intersect at point P. If TKE= x+6 and IEK= 2x, find IKE
Answers
The length of IKE is 2x - 12.
What is equation?A condition on a variable that is true for just one value of the variable is called an equation.
Since KITE is a kite, we know that KT = IT and KE = IE. Let's call the length of these diagonals d. Then we have:
KT + TI = d
KE + EI = d
Substituting in the given values, we get:
x + 6 + 2x = d
2x + IE = d
Solving for d in the first equation, we get:
3x + 6 = d
Substituting this into the second equation, we get:
2x + IE = 3x + 6
Solving for IE, we get:
IE = x + 6
Therefore, IKE is equal to:
IKE = IT - IE
IKE = (d - KT) - (x + 6)
IKE = (3x + 6 - x - 6) - (x + 6)
IKE = 2x - 12
So, the length of IKE is 2x - 12.
Learn more about equation on:
https://brainly.com/question/27893282
#SPJ4

please help I will give you any award

Answers
Answer:
218.57
Step-by-step explanation:
Since it is an isoceles triangle, the sides are 32, 32, and 14.
Using Heron's Formula, which is Area = sqrt(s(s-a)(s-b)(s-c)) when s = a+b+c/2, we can calculate the area.
(A+B+C)/2 = (32+32+14)/2=39.
A = sqrt(39(39-32)(39-32)(39-14) = sqrt(39(7)(7)(25)) =sqrt(47775)= 218.57.
Hope this helps have a great day :)
Check the picture below.
so let's find the height "h" of the triangle with base of 14.
\(\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies o=\sqrt{c^2 - a^2} \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{32}\\ a=\stackrel{adjacent}{7}\\ o=\stackrel{opposite}{h} \end{cases} \\\\\\ h=\sqrt{ 32^2 - 7^2}\implies h=\sqrt{ 1024 - 49 } \implies h=\sqrt{ 975 }\implies h=5\sqrt{39} \\\\[-0.35em] ~\dotfill\)
\(\stackrel{\textit{area of the triangle}}{\cfrac{1}{2}(\underset{b}{14})(\underset{h}{5\sqrt{39}})}\implies 35\sqrt{39} ~~ \approx ~~ \text{\LARGE 218.57}\)

of the cartons produced by a company, 3% have a puncture, 6% have a smashed corner, and 1.4% have both a puncture and a smashed corner. find the probability that a randomly selected carton has a puncture or a smashed corner.
Answers
The probability that a randomly selected carton has a puncture or a smashed corner is 0.076, or 7.6%.
What is probability?
Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain to happen.
To find the probability that a randomly selected carton has a puncture or a smashed corner, we can use the formula:
P(puncture or smashed corner) = P(puncture) + P(smashed corner) - P(puncture and smashed corner)
where P(puncture) is the probability of a carton having a puncture, P(smashed corner) is the probability of a carton having a smashed corner, and P(puncture and smashed corner) is the probability of a carton having both a puncture and a smashed corner.
Substituting the given probabilities into the formula, we get:
P(puncture or smashed corner) = 0.03 + 0.06 - 0.014
P(puncture or smashed corner) = 0.076
Therefore, the probability that a randomly selected carton has a puncture or a smashed corner is 0.076, or 7.6%.
To learn more about probability from the given link:
https://brainly.com/question/30034780
#SPJ1
Which two points should the line of best fit go through to best represent the data in the scatter plot?
A. (1,3) and (2,7)
B. (1,3) and (6,13)
C. (3,8) and (5,12)
D. (5,12) and (6,13)

Answers
Answer: the answer is c I think
Step-by-step explanation:
How do you write 3.37 as a percentage?
Answers
Answer:
Step-by-step explanation:
What is 3.37 as a percent?
To write 3.37 as a percent have to remember that 1 equal 100% and that what you need to do is just to multiply the number by 100 and add at the end symbol % .
3.37 * 100 = 337%
And finally we have:
3.37 as a percent equals 337%
Answer:
337%
Step-by-step explanation:
3.37x100=337
If I were to solve for x and there is x to the third power equals to 64. What would be my answer?
Answers
Answer:
x=4
Step-by-step explanation:
if you do \(\sqrt[3]{64}\) you'll get that \(4^{3}\) is 64.
An aquarium is 0.5 feet wide, 1.5 feet tall, and 2 feet long. The bottom is covered with gravel to a height of 3 inches. The tank will be filled with water to 3 inches below the top. How many gallons of water are needed to fill the aquarium? Ignore any water that might seep into the layer of gravel. Round to the nearest tenth.
Answers
So the amount of water needed to fill the aquarium is approximately 1.87 gallons. This is our final answer, rounded to the nearest tenth.
To calculate the amount of water needed to fill the aquarium, we first need to find the volume of the tank. To do this, we can use the formula for the volume of a rectangular prism, which is:
Volume = length x width x height
Plugging in the measurements given in the problem, we get:
Volume = 2 feet x 0.5 feet x 1.5 feet
Volume = 0.75 cubic feet
Next, we need to convert cubic feet to gallons. There are 7.48 gallons in one cubic foot, so we can multiply the volume by 7.48 to get the amount of water in gallons:
0.75 cubic feet x 7.48 gallons/cubic foot = 5.61 gallons
However, we need to subtract the amount of space taken up by the gravel and the water that won't be filled to the top of the tank. The layer of gravel takes up 3 inches at the bottom of the tank, which is 0.25 feet. To find the volume of the gravel, we can use the same formula:
Volume = length x width x height
Volume = 2 feet x 0.5 feet x 0.25 feet
Volume = 0.25 cubic feet
We also need to subtract the volume of water that won't be filled to the top. The tank will be filled to a height of 1.25 feet (1.5 feet - 0.25 feet for the gravel), but we need to leave a 3-inch gap at the top. This gap is 0.25 feet, so we can find the volume of the unfilled space:
Volume = length x width x height
Volume = 2 feet x 0.5 feet x 0.25 feet
Volume = 0.25 cubic feet
Now we can subtract the volume of the gravel and unfilled space from the total volume of the tank:
Total volume - volume of gravel - volume of unfilled space = volume of water
0.75 cubic feet - 0.25 cubic feet - 0.25 cubic feet = 0.25 cubic feet
Finally, we can convert this to gallons:
0.25 cubic feet x 7.48 gallons/cubic foot = 1.87 gallons
So the amount of water needed to fill the aquarium is approximately 1.87 gallons. This is our final answer, rounded to the nearest tenth.
To know more about nearest tenth visit:-
https://brainly.com/question/12102731
#SPJ11
Can someone help me out (giving brainliest)

Answers
Answer:
D. 1500 π
Step-by-step explanation:
V=πr²h
r=10
h = 15
10²=100
100 x 15 = 1500
1500π
Answer:
option D is a correct answer...
Which statements are true? SELECT ALL THAT APPLY

Answers
Answer:
C
Step-by-step explanation:
AC & BC are adjacent sides.
If two sides share a vertex, then they are adjacent sides
The velocities of commuter trains A and B are as shown(A=66,B=48). Knowing that the speed of each train is constant and that B reaches the crossing 10 min after A passes through the same crossing, determine a) the relative velocity of B with respect to A, b)the distance between the fronts of the engines 3 min after A passed through the crossing.
Answers
The relative velocity of B with respect to A is -18 km/h and the distance between the fronts of the engines 3 min after A passed through the crossing is 3.6 km.
a) The relative velocity of train B with respect to train A is correct.
b) To find the distance between the fronts of the engines 3 minutes after A passed through the crossing, we need to take into account that B takes an additional 10 minutes to reach the crossing after A passes through it. Therefore, the time elapsed since the two trains were at the crossing together is 13 minutes.
The distance that A has covered in 13 minutes is:
distance = velocity x time
distance = 66 km/h x (13/60) h
distance = 14.3 km
At the same time, B has covered:
distance = velocity x time
distance = 48 km/h x (13/60) h
distance = 10.4 km
So the distance between the fronts of the engines 13 minutes after they were at the crossing together is:
distance = 14.3 km - 10.4 km
distance = 3.9 km
Therefore, the distance between the fronts of the engines 3 minutes after A passed through the crossing is:
distance = 3.9 km - (66 km/h x (3/60) h)
distance = 3.6 km
Hence, the correct answer for part b) is that the distance between the fronts of the engines 3 minutes after A passed through the crossing is 3.6 km.
To learn more about velocity:
https://brainly.com/question/80295?source=archive
#SPJ11
The expression -x^2 + 70x -600 represents a companys profit for selling x items. For which number of items sold is the companys profit equal to zero?
Answers
Answer:
Step-by-step explanation:
-x² + 70x - 600
If we multiply all by -1, we have
x² - 70x + 600
If we factorise this, we have
x² - 10x - 60x + 600
x(x - 10) - 60(x - 10)
(x - 10) (x - 60)
x = 10
x = 60
If the company sells 10, or 60 items, their profit is 0
A sword smith pulls a blade out of the forge at 1000C. To lower the temperature he plunges the steel into a oil bath. Every second the sword is in the oil the temperature goes down by 60% . What is the sword’s temperature 8 seconds after being submerged?
Answers
Answer:
After 8 seconds, the sword's temperature would be approximately 51.2°C.
Step-by-step explanation:
I got it right.
Alicia buys a fish tank. The dimensions of the fish tank are 80 cm x 35cm x 40cm. Alicia fills the tank with water to 4/5 of the height of the tank. What is the mass of the water in the fish tank? "I know that 1 cm of water has a mass of 1 gram." Give your answer in kilograms.
Answers
Answer: 89.6 kg of water
Step-by-step explanation:
Find the total volume of the tank:
(80cm)*(35cm)*(40cm) = 112,000 cm^3
4/5 of this would be 89,600 cm^3
Water has a mass of 1 gram/cm^3
(1 gram/cm^3)*(89,600 cm^3) = 89,600 g of water
(89,600 g)*(1 kg/1,000 g) = 89.6 kg of water
Someone please help me

Answers
Answer:
Solutions: \(x = \frac{-3}{ 4} + i \sqrt{39}\), \(x = \frac{-3}{4} - i \sqrt{39}\)
Step-by-step explanation:
Given the quadratic equation, 2x² + 3x + 6 = 0, where a =2, b = 3, and c = 6:
Use the quadratic equation and substitute the values for a, b, and c to solve for the solutions:
\(x = \frac{-b +/- \sqrt{b^{2} - 4ac} }{2a}\)
\(x = \frac{-3 +/- \sqrt{3^{2} - 4(2)(6)} }{2(2)}\)
\(x = \frac{-3 +/- \sqrt{9- 48} }{4}\)
\(x = \frac{-3 +/- \sqrt{-39} }{4}\)
\(x = \frac{-3 + i \sqrt{39} }{4}\), \(x = \frac{-3 - i \sqrt{39} }{4}\)
Therefore, the solutions to the given quadratic equation are:
\(x = -\frac{3}{ 4} + i \sqrt{39}\) , \(x = -\frac{3}{4} - i \sqrt{39}\)
A publisher needs to send many books to a local book retailer and will send the books in a combination of small and large boxes. Each small box can hold 20 books and each large box can hold 35 books. There were twice as many small boxes sent as large boxes, which altogether can hold 225 books. Determine the number of small boxes sent and the number of large boxes sent.
Answers
A publisher needs to send many books to a local book retailer and will send the books in a combination of small and large boxes. Each small box can hold 20 books and each large box can hold 35 books.
The system of equation will be x+y = 7 and 20x+35y = 225.
Let x be the no of small boxes and y be the no. of large boxes.
Given here each small box can hold 20 books and each large box can hold 35 books.
A total of 7 boxes were sent.
So, x+y = 7.......equation 1
Also given that 7 boxes can hold 225 books altogether.
So, 20x+35y = 225.....equation 2
Hence the system of equation will be x+y = 7 and 20x+35y = 225.
To learn more combinations click here https://brainly.com/question/11732255
#SPJ4
write the phrase "6 more than 8 divided by x is 10" as a variable expression
Answers
Hi there!
phrase:6+(8/x)=10
1. Break all meaning apart:
6 more than 8 by x= 6+8/x
is 10 meaning the total is ten...
2.Add them together:
6+(8/x)=10
Therefore, the phrase for “6 more than 8 divided by x is 10” as a variable expression will be 6+(8/x)=10.
if x is a positive integer, r is the remainder when x is divided by 4, and r is the remainder when x is divided by 9, what is the greatest possible value of r2 r ?
Answers
As per the remainder that the greatest possible value of 17
The term remainder in math defined as if a number is not completely divisible by another number then we are left with a value once the division is done
Here we have if x is a positive integer, then r is the remainder when x is divided by 4 and r is the remainder when x is divided by 9.
As we all know that the remainder is always smaller than the divisor.
Here we have also know that it will be 0 if the dividend is evenly divisible or a positive integer less than the divisor.
So, when we divided by 4 then the largest remainder will be 3 and then here we have to divided by 9, then the largest remainder will be written as
=> r² + R = 32 + 8
=> 9 + 8 = 17
To know more about remainder here.
https://brainly.com/question/11360783
#SPJ4