A particle is moving with the given data. Find the position of the particle. v(t) = sin(t) - cos(t), s(0) = 8
s(t) = ...
Answers
The position function is s(t) = -cos(t) - sin(t) + 9 found by using the given velocity function v(t) = sin(t) - cos(t) and initial position s(0) = 8.
To find the position function s(t), we need to integrate the velocity function v(t) with respect to time.
∫v(t)dt = ∫sin(t) - cos(t) dt
Using the integration formulas, we get
∫sin(t)dt = -cos(t) + C1
and
∫cos(t)dt = sin(t) + C2
where C1 and C2 are constants of integration.
Therefore,
∫v(t)dt = -cos(t) + sin(t) + C
where C = C2 - C1 is the constant of integration.
To determine the constant C, we use the initial position s(0) = 8.
s(0) = -cos(0) - sin(0) + C = -1 + C = 8
Thus, C = 9.
Therefore, the position function is
s(t) = -cos(t) - sin(t) + 9.
For more questions like Function click the link below:
https://brainly.com/question/16008229
#SPJ11
Related Questions
Which is an example of a line segment? the edge of a book the corner of a box a beam of light the floor of a classroom
Answers
(D) the floor of a classroom is a perfect example of a line segment.
What do we mean by line segment?A line segment is a section of a straight line that is constrained by two distinct end points and contains every peak on the line between them. The Euclidean distance between the endpoints of a line segment determines its length. A closed line segment contains both endpoints, whereas an open line segment does not; a half-open line segment contains only one endpoint. In real life, a line segment can be represented by a ruler, a pencil, or a stick. The sun's rays are an illustration of a ray. The sun is the origin of the sun's rays, but there is no endpoint. A line segment is a perfect example of a classroom floor.Therefore, (D) the floor of a classroom is a perfect example of a line segment.
Know more about line segments here:
https://brainly.com/question/2437195
#SPJ4
The correct form of the question is given below;
Which is an example of a line segment?
(A) the edge of a book
(B) the corner of a box
(C) a beam of light
(D) the floor of a classroom
If the distribution of observations were perfectly symmetrical and unimodal,
A the mean would be greater than the mode
B the mean, median mode would be the same
C the mode would be lesser than the median
D the median would be greater than the mean
Answers
If the distribution of observations were perfectly symmetrical and unimodal, option B) The mean, median, and mode would be the same.
In a perfectly symmetrical and unimodal distribution, the mean, median, and mode would be equal. This is because in such a distribution, the data would be evenly spread around a central value. The mean is calculated by summing all the observations and dividing by the total number of observations. Since the distribution is symmetrical, the sum of the observations on one side of the central value would be equal to the sum on the other side, resulting in a balanced mean.
The median is the middle value when the observations are arranged in ascending or descending order. In a symmetrical distribution, the middle value would be the same as the central value, leading to the median being equal to the mean.
The mode represents the value that appears most frequently in the distribution. In a perfectly symmetrical and unimodal distribution, all values would occur with the same frequency, resulting in multiple modes. However, since the distribution is unimodal, meaning it has only one peak, all the modes would coincide, and the mode would also be equal to the mean and median. Therefore, in a perfectly symmetrical and unimodal distribution, the mean, median, and mode would all be the same value, leading to answer B) The mean, median, and mode would be the same.
Learn more about median here: brainly.com/question/30891252
#SPJ11
1. Lee likes to have a lunch as a vegetable salad and a hot drink. Each salad contains 5 types of ingredients out of the following: cucumbers, tomatoes, spinach, cauliflower, sweet pepper, carrots, celery and avocado. Hot drinks are: black coffee, cappuccino, latte, cocoa and 5 types of teas. Only cappuccino, latte, and cocoa contain milk. Lee doesn't mix cucumbers and/or tomatoes with milk. How many different lunches can Lee create
Answers
Lee can create a total of 40 different lunches consisting of a vegetable salad and a hot drink. This is calculated by multiplying the number of options for the salad (5 ingredients) with the number of options for the hot drink (8 options excluding milk).
To calculate the number of different lunches, we start by considering the options for the vegetable salad. Lee can choose 5 ingredients out of the 8 available options (cucumbers, tomatoes, spinach, cauliflower, sweet pepper, carrots, celery, and avocado).
This gives us 8 choose 5, which is equal to 8! / (5! * (8-5)!) = 56 possible combinations of ingredients for the salad.
Next, we consider the options for the hot drink. There are 5 types of teas (excluding milk) and 3 options (cappuccino, latte, and cocoa) that contain milk. So, there are a total of 5 + 3 = 8 options for the hot drink.
However, since Lee doesn't mix cucumbers and/or tomatoes with milk-containing drinks, we need to subtract the 3 milk-containing options from the total options for the hot drink. Therefore, Lee has 8 - 3 = 5 options for the hot drink.
To calculate the total number of different lunches, we multiply the number of salad combinations (56) with the number of hot drink options (5). Thus, Lee can create a total of 56 * 5 = 280 different lunches consisting of a vegetable salad and a hot drink.
To learn more about permutations click here: brainly.com/question/29855401
#SPJ11
(PLEASE ANSWER-)
Given the equation five eighths plus h equals eleven over eight, determine the value of h.
six eighths
sixteen over eighteen
fifty five over sixty four
eight over six
Answers
The value of h in the equation five eighths plus h equals eleven over eight is six eighths
How to solve an equation?An equation is a mathematical expression that contains two or more numbers and variables linked together by mathematical operations such as exponents, multiplication, division, addition, subtraction and so on.
Given the equation five eighths plus h equals eleven over eight, it is represented as:
(5/8) + h = 11/8
multiply the both sides of the equation by 8:
(5/8) * 8 + h * 8 = (11/8) * 8
5 + 8h = 11
subtract 5 from both sides:
5 + 8h - 5 = 11 - 5
8h = 6
divide both sides by 8:
8h/8 = 6/8
h = 6/8
The value of h is 6/8
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
Jenny, Rachel and Angela sing a song which consists of three equal lines. Rachel starts to sing as Jenny is starting the second line. Angela starts singing as Jenny is starting the third line. Each person sings the whole song four times without a break and then stops. The fraction of the total singing time that all three are singing at the same time is
Answers
Using expression (L/3) / (36t) = L / (108t), the fraction of the total singing time that all three are singing at the same time is L / (108t).
What exactly are expressions?
In mathematics, an expression is a combination of numbers, variables, and operations that represents a value or a quantity. Expressions can be composed of one or more terms, which are separated by addition or subtraction symbols.
For example, the expression 2x + 3y - 5 represents a value that depends on the values of the variables x and y. The term 2x represents a quantity that is twice the value of x, the term 3y represents a quantity that is three times the value of y, and the term -5 represents a constant value of negative five.
Now,
Let's call the length of the song "L" and the time it takes to sing one line "t". Then, we know that:
Rachel starts singing at t = 0, and she sings for a total of 4L.
Jenny starts singing at t = t, and she sings for a total of 4L.
Angela starts singing at t = 2t, and she sings for a total of 4L.
Since each line of the song is the same length, we can divide the total singing time for each person into three equal parts, one for each line. So, each person sings for a total of 12t.
Now, let's think about when all three people are singing at the same time. This happens during the second line of the first repetition of the song. Rachel is singing the first line, Jenny is singing the second line, and Angela is starting to sing the third line. The total length of time that all three people are singing together is just the length of one line, which is L/3.
Since each person sings for a total of 12t, the total singing time for all three people is 36t. Therefore, the fraction of the total singing time that all three are singing at the same time is:
(L/3) / (36t) = L / (108t)
So, the fraction of the total singing time that all three are singing at the same time is L / (108t).
To know more about expressions visit the link
brainly.com/question/13947055
#SPJ1
Rewrite in radical form 3^(2/5)
Answers
Answer:
Convert to radical form using the formula
axn=n√ax.
Exact Form:5√32
Decimal Form:
1.55184557
…
Step-by-step explanation:
A clay specimen, 25 mm thick, has been tested in an oedometer apparatus with two way rainage, and it is observed that 50% of the consolidation settlement occurs in 1 hour. A ayer of the same clay is observed to settle 10 mm in 10 years and after many years to settle (total primary consolidation) by 35 mm. Determine the thickness of the clay layer if it drains only from upper surface
Answers
The thickness of the clay layer, which drains only from the upper surface, can be determined based on the consolidation settlement observations. With 50% of consolidation settlement occurring in 1 hour for a 25 mm thick specimen, and a total primary consolidation settlement of 35 mm occurring over many years, the thickness of the clay layer is approximately 87.5 mm.
The consolidation settlement of a clay specimen can be used to estimate the thickness of a clay layer that drains only from the upper surface. In this case, the observed settlement data provides valuable information.
Firstly, we know that 50% of the consolidation settlement occurs in 1 hour for a 25 mm thick clay specimen. This is an important parameter for calculating the coefficient of consolidation (Cv) using Terzaghi's theory. From the Cv value, we can estimate the time required for full consolidation settlement.
Secondly, we are given that the same clay settles 10 mm over 10 years and eventually settles a total of 35 mm over a longer period. This long-term settlement is known as the total primary consolidation settlement. By comparing this settlement value with the settlement data from the oedometer test, we can determine the thickness of the clay layer.
To calculate the thickness, we can use the concept of the consolidation settlement ratio. The ratio of the total primary consolidation settlement to the consolidation settlement at 50% completion is equal to the ratio of the total thickness to the thickness at 50% completion. Applying this ratio, we can determine that the thickness of the clay layer, which drains only from the upper surface, is approximately 87.5 mm.
To learn more about thickness click here: brainly.com/question/23622259
#SPJ11
The pile of papers is 6. 5 mm thick and it consist of 100 sheets of paper dimensions
21. 5 cm x 29. 7 cm. the density of paper is 1. 20 cm. find the mass of one sheet of
paper.
Answers
Therefore , the solution to the given problem of the volume comes out to be mass = 4.98grams
Defines volumethe volume that something takes up in three dimensions. Think about the potential amount of water. also known as capacity.In this case, the volume is 200 units since area * height (10 x 4 x 5). 3 Volume units include: • The liter, cubic centimeter, and cubic meter are all metric units (m3)• Units used in the US are ounces, pints, gallons, cubic inches, and cubic feet.
Here,
Employing the formula
solving for mass yields density=mass/volume.
density times volume equals mass.
Length, width, and height are all equal in volume.
Where
length=29.7cm
is 21.5 centimeters wide.
By translating 6.5mm to cm and dividing by 100, one may get the height of a single sheet of paper.
Given that 10mm = 1 cm, 6.5mm*1 cm = 0.65 cm
Divide the pile's thickness by 100 to get
0.65/100= 0.0065cm.
Currently, one sheet of paper has a volume of 4.15 cm3 (=29.7 * 21.5 * 0.0065).
mass=density*volume
paper sheet mass = (1.2g/cm3)*(4.15cm3) = 4.98grams
Therefore , the solution to the given problem of the volume comes out to be mass = 4.98grams.
To know more about volume , visit
brainly.com/question/1578538
#SPJ4
Subtract.
3x−5x−4−x2+12x−17x2−16
Answers
Step-by-step explanation:
3x - 5x - 4 - x^2 + 12x - 17x^2 - 16
= -2x - 20 - 18x^2 + 12x
= 10x - 20 - 18x^2
Hope it helpz~ uh..
What is tan 30°?
60'
2
1
90
30"

Answers
Answer:
Option F. 1/√3
Step-by-step explanation:
From the question given above, the following data were obtained:
Angle θ = 30°
Opposite = 1
Adjacent = √3
The value of Tan 30° can be obtained as illustrated below:
Tan θ = Opposite / Adjacent
Tan 30 = 1/√3
Thus, the value of Tan 30° is 1/√3
an angle in standard position is a positive angle if the generating line, the terminal side, is rotated counterclockwise. question 5 options: true false
Answers
The given statement is TRUE
If an angle is counterclockwise then the angle is said to be positive.
We can conclude and find the explanation such that,
If any angle is measured in the direction equivalent to counterclockwise from the starting point of the terminal side then that angle is termed a positive angle whereas if an angle is measured from the direction clockwise then the angle is termed as a negative angle.
Refer to the attached images to find the phenomenon of positive and negative angles.
For example: According to the first figure let us draw an angle of 90°
We will calculate this angle as = \(\frac{90}{360}\)
= 1/4
Thus, moving counterclockwise in the positive x-axis.
According to the second figure let us draw the angle of 360°
We will calculate this angle as = \(\frac{360}{360}\)
= 1
Thus, 1 complete rotation is done around the circle moving counterclockwise from the positive side of the x-axis.
Therefore,
The given statement is TRUE
If an angle is counterclockwise then the angle is said to be positive.
To know more about Counterclockwise and Clockwise angles,
https://brainly.com/question/17912716
#SPJ4

You invest $20,000 in the stock market. The stock market then plummets
over the next few weeks. Each day, your investment loses half of its value. How
much will you have invested after 14 days? Write the geometric sequence
formula and show all of your work.
Answers
After 14 days, you will have approximately $2.4414 invested in the stock market.
The amount you will have invested after 14 days can be calculated using the geometric sequence formula. The formula for the nth term of a geometric sequence is given by:
an = a1 x \(r^{(n-1)\)
Where:
an is the nth term,
a1 is the first term,
r is the common ratio, and
n is the number of terms.
In this case, the initial investment is $20,000, and each day the investment loses half of its value, which means the common ratio (r) is 1/2. We want to find the value after 14 days, so n = 14.
Substituting the given values into the formula, we have:
a14 = 20000 x\((1/2)^{(14-1)\)
a14 = 20000 x \((1/2)^{13\)
a14 = 20000 x (1/8192)
a14 ≈ 2.4414
Therefore, after 14 days, you will have approximately $2.4414 invested in the stock market.
For more such answers on ratio
https://brainly.com/question/12024093
#SPJ8
The amount you will have invested after 14 days is given as follows:
$2.44.
What is a geometric sequence?A geometric sequence is a sequence of numbers where each term is obtained by multiplying the previous term by a fixed number called the common ratio q.
The explicit formula of the sequence is given as follows:
\(a_n = a_1q^{n-1}\)
In which \(a_1\) is the first term of the sequence.
The parameters for this problem are given as follows:
\(a_1 = 20000, q = 0.5\)
Hence the amount after 14 days is given as follows:
\(a_{14} = 20000(0.5)^{13}\)
\(a_{14} = 2.44\)
More can be learned about geometric sequences at https://brainly.com/question/24643676
#SPJ1
A survey was done that asked people to indicate whether they preferred to ride a
street bike or a mountain bike. The results of the survey are shown in the two-way
table.
Amjed is making a relative frequency table from this data.
What operation should Amjed perform to determine the relative frequency of a
person over 30 years old who prefers to ride a mountain bike? 1) Subtract 25 from 462, then divide by 462. 2) Divide 25 by 462. 3) Add 180 to 462, then divide by 463. 4) Divide 180 by 462

Answers
The operation that Amjed should perform to determine the relative frequency of a person over 30 years old who prefers to ride a mountain bike is given as follows:
2) Divide 25 by 462.
How to calculate a probability?The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes, hence it is the same as a relative frequency.
The total number of people is given as follows:
58 + 164 + 215 + 25 = 462.
Out of these people, 25 prefer mountain bike, hence the relative frequency is given as follows:
25/462.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1
In one afternoon's shopping Seedevi spent half as much money as Georgia, but $6 more than Amy. If the three of them spent a total of $258, how much did Seedevi spend?
Answers
The amount spent by Seedevi is $66
How to determine the amount spent by Seedevi?From the question, the given parameters are:
Seedevi = half as much money as Georgia,
Seedevi = $6 more than Amy
The three of them = $258
To solve this question, we use the following representations
x = Seedevi
y = Georgia
z = Amy
So, we have the following equations
x = 0.5y
x = 6 + z
x + y + z = 258
Make y and z the subjects
y = 2x
z = x - 6
Substitute y = 2x and z = x - 6 in x + y + z = 258
x + 2x + x - 6 = 258
Evaluate the like terms
4x = 264
Divide by 4
x = 66
Hence, the amount spent by Seedevi is $66
Read more about equations at:
https://brainly.com/question/2972832
#SPJ1
In the triangle, suppose that mD=(x+7), mZE-(4x-3), and mZF= (3x)".
Check
(a) Write an equation to find x. Make sure you use an* sign in your answer.
Equation:
(b) Find the degree measure of each angle.
m2D-
m2E-
m2F-
X

Answers
Answer:
(a) Equation: (x + 7) + (4x - 3) + (3x) = 180
(b) m ∠D = 29°, m ∠E = 85°, and m ∠F = 66°
Step-by-step Explanation:
(a): According to the triangle sum theorem, the sum of the interior angles of a triangle equals 180°. Thus, setting the sum of the angles equal to 180 allows us to find x:
m ∠D + m ∠E + m ∠F = 180
Equation: (x + 7) + (4x - 3) + (3x) = 180°
(b):
Step 1: First, we need to find x:
(x + 7) + (4x - 3) + (3x)
(x + 4x + 3x) + (7 - 3) = 180
8x + 4 = 180
8x = 176
x = 22
Step 2: Now we can plug in 22 for x for each expression representing the angle measures:
Plugging in 22 for x in ∠D expression:
m ∠D = (22 + 7)
m ∠D = 29°
Plugging in 22 for x in ∠E expression:
m ∠E = 4(22) -3
m ∠E = 88 - 3
m ∠E = 85°
Plugging in 22 for x in ∠F expression:
m ∠F = 3(22)
m ∠F = 66°
Optional Step 3: We can check that the sum of the three angles we've found equals 180:
29 + 85 + 66 = 180
114 + 66 = 180
180 = 180
Please answer correctly !!!!!!!! Will mark brainliest !!!!!!!!!!
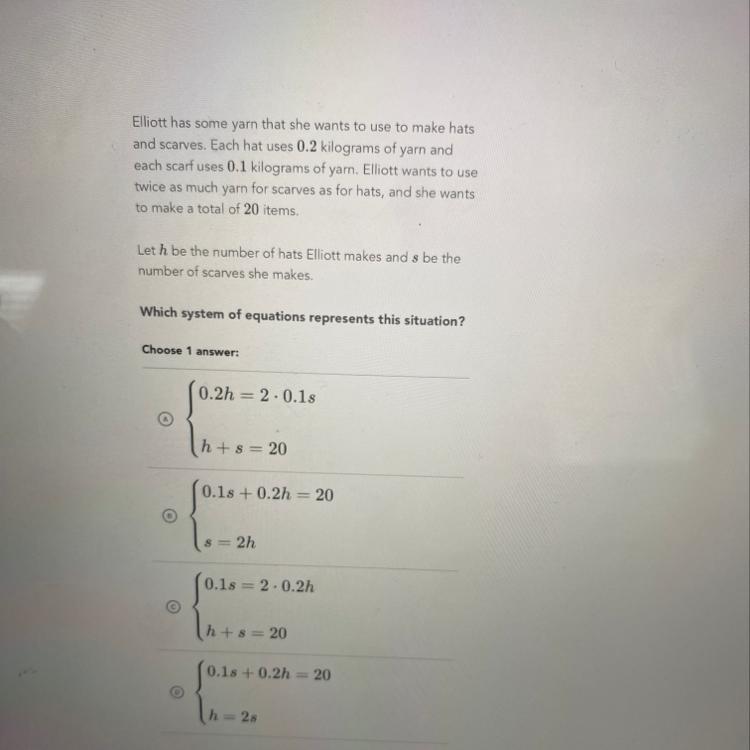
Answers
Answer:
The equation are:
1) h + s = 20
2) 4h = 1s
Step-by-step explanation:
Number of hats Elliott made = h
Number of scarfs Elliott made = s
total number of items Elliott made = 20
h + s = 20 ..[1]
1 hat uses 0.2 kilograms of yarn
1 hat = 0.2 kg of yarn
Then h hats will use = 0.2h kg of yarn
1 scarf uses 0.1 kilograms of yarn
1 scarf= 0.1 kg of yarn
Then s scarfs will use = 0.1s kg of yarn
She wants to twice as much as yarn for scarves for hats:
2 × (0.2h kg of yarn) = 0.1s kg of yarn
0.4h = 0.1s
4h = 1s...[2]
The equation are:
1) h + s = 20
2) 4h = 1s
Answer:C
0.1s=2•0.2h
H+S=30
Step-by-step explanation: I did it on khan
Which of the following sets represents the solution of the equation below?
-3/2x² = x+1
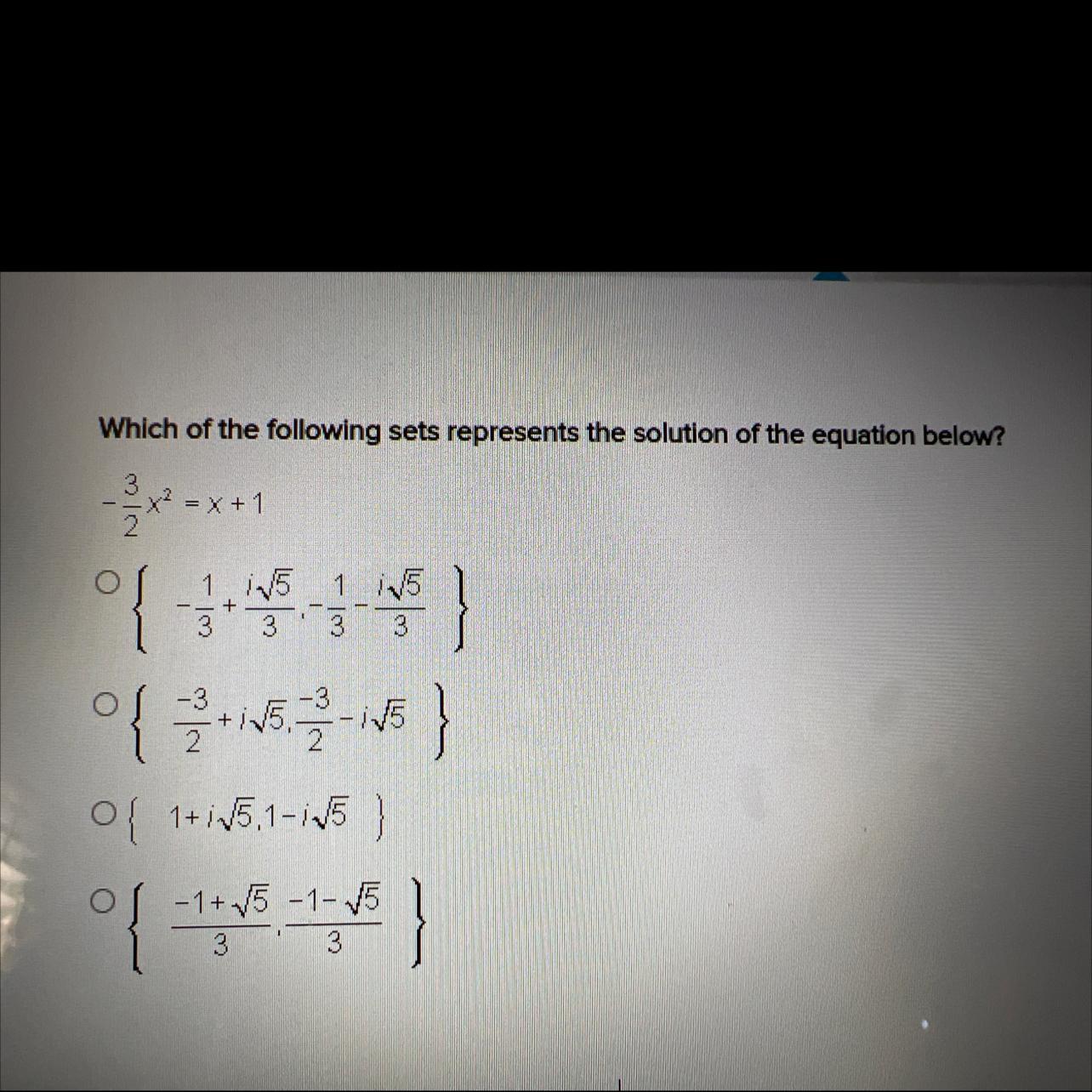
Answers
The solution set is: \($\left{\frac{-1+\sqrt{5}}{3}, \frac{-1-\sqrt{5}}{3}\right}$\)
Option (D) is correct.
What is a quadratic equation?
A quadratic equation is a type of equation in algebra that can be written in the form of ax^2 + bx + c = 0, where x is the unknown variable, and a, b, and c are constants with a not equal to zero
The equation is:
\($-\frac{3}{2}x^2 = x + 1$\)
We can rewrite this equation as:
\($-\frac{3}{2}x^2 - x - 1 = 0$\)
To solve for x, we can use the quadratic formula:
\($x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$\)
Where a = -3/2, b = -1, and c = -1. Substituting these values into the quadratic formula, we get:
\($x = \frac{-(-1) \pm \sqrt{(-1)^2 - 4(-\frac{3}{2})(-1)}}{2(-\frac{3}{2})}$\)
Simplifying this expression, we get:
\($x = \frac{1 \pm \sqrt{5}}{3}$\)
Therefore, the solution set is:
\($\left{\frac{-1+\sqrt{5}}{3}, \frac{-1-\sqrt{5}}{3}\right}$\)
To learn more about the quadratic equations, visit:
https://brainly.com/question/1214333
#SPJ1
dr. anderson wants to know if annual income differs between college graduates and non-college graduates. he should use a(n)
Answers
Anderson should use a two-sample t-test to determine if there is a statistically significant difference in annual income between college graduates and non-college graduates.
A two-sample t-test is a type of inferential statistic used to compare the means of two independent groups. It is used to determine if the difference between the two groups is statistically significant.
In this case, Anderson would compare the mean annual income of college graduates to the mean annual income of non-college graduates. If the difference between the two means is statistically significant, then Anderson can conclude that there is a difference in annual income between college graduates and non-college graduates.
If the difference is not statistically significant, then Anderson can conclude that there is no difference in annual income between the two groups.
For more questions like Two-sample t-test click the link below:
https://brainly.com/question/15870238
#SPJ4
recursion is sometimes required to solve certain types of problems. true/false
Answers
True. Recursion is often necessary to solve certain types of problems that exhibit a recursive structure or require repeated subproblem solving.
Recursion is a programming technique where a function calls itself in its own definition. It allows for the decomposition of complex problems into smaller, more manageable subproblems that can be solved recursively. Recursion is particularly useful when problems exhibit a recursive structure, such as tree traversal, backtracking, or divide-and-conquer algorithms.
For example, problems like computing the factorial of a number, calculating Fibonacci numbers, or traversing a binary tree can be elegantly and efficiently solved using recursion. These problems can be broken down into smaller instances of the same problem until a base case is reached, and then the solutions are combined to solve the original problem.
However, it's worth noting that not all problems require recursion for their solution. There are alternative approaches, such as iterative loops or dynamic programming, which can be used depending on the problem's characteristics and requirements.
To learn more about Recursion click here, brainly.com/question/30063488
#SPJ11
Katya decided that she could not afford the $48,000 it would cost her to attend college and get her four-year degree. Instead, she entered the full-time workforce four years earlier than her peers who went to college. During those four years, she earned a total of $90,000. However, without a college degree, Katya made an average of $10,000 less than she could have with a degree every year for the 40 additional years of her career. What was the long-term financial cost of Katya deciding to not attend college?
Answers
Answer: $310,000
Step-by-step explanation:
In 40 additional years, the amount she made less than her college counterparts was;
= 10,000 * 40
= $400,000
She however made $90,000 more than them as they went to college;
= 400,000 - 90,000
= $310,000
The long-term financial cost was $310,000.
Demetrius is training for the same 1-mile race.
Demetrius ran at a constant speed of 7.5 miles per hour.
Yosef's progress is shown by the graph.
Who finished the mile first?

Answers
Yosef finished the mile in 9 minutes.
Distance = 1 mile
Demetrius' speed = 7.5 miles per hour
Demetrius' time = Distance/speed
= 8 minutes
Demetrius finished the mile first by taking 1 minute less than Yosef's finishing time.
Answer:
Demetrius wins the race by 7.5 minutes.Step-by-step explanation:
We know that:
Demetrius = 7.5 miles = 60 minutesYosef = 1 mile = 9 minutesLet's see how much time Yosef take in 7.5 miles.
Solution:
Yosef speed = 1 mile = 9 minutes=> 7.5 miles = 9 x 7.5 minutes=> 7.5 miles = 67.5 minutes60 minutes < 67.5 minutesAfter working on this problem, we can conclude that Demetrius wins the race by 7.5 minutes.
A small business spend $23,000 for taxable items last year. The tax rate was 9.5%. How much did the small business pay in taxes last year?
Answers
Answer:
$2,185
Step-by-step explanation:
Multiply the amount spent by the tax rate.
23,000 x 9.5% = $2,185
Ella has a mass of 56 kg, and Tyrone has a mass of 68 kg. Ella is standing at the top of a skateboard ramp that is
1.5 meters tall. Which conclusion is best supported by the given information?
If Tyrone stands at the top of the same ramp, his potential energy will be less than Ella's
If Tyrone stands at the top of a 1 m high ramp, his potential energy will be greater than Ella's.
If Tyrone stands at the top of the same ramp, his potential energy will be the same as Ella's.
If Tyrone stands at the top of a 2 m high ramp, his potential energy will be greater than Ella's.
Hey
Answers
Step-by-step explanation:
Given that,
Mass of Ella is 56 kg and mass of Tyrone is 68 kg.
Position of Ella is 1.5 m on the ramp.
Potential energy of an object is given by :
P = mgh
It is directly proportional to the position of an object.
If Tyrone stands at the top of ramp at more height than Ella, it will have more potential energy. Hence, the correct option is (d) "If Tyrone stands at the top of a 2 m high ramp, his potential energy will be greater than Ella's."
Answer:
it would be d.
Step-by-step explanation:
got it right on the test
Find the slope of the line passing through each of the following pairs of points and draw the graph of the line. (−4, −1), (2, 3)
Answers
Answer:
2/3
Step-by-step explanation:
To find slope the formula is (y2-y1)/(x2-x1).
Using that we substitute the pairs.
(-4,-1), (2,3) would then be (x1, y1), (x2, y2)
so you solve from there.
the equation would be ( 3 - ( - 1 ) ) / ( 2 - ( - 4 ).
( 3 - ( - 1 ) ) / ( 2 - ( - 4 )
( 3 + 1 ) / ( 2 + 4 )
4 / 6
2 / 3
The slope of the line passing through the points (−4, −1), (2, 3) will be 2/3
What is a slope?Slope or the gradient is the number or the ratio which determines the direction or the steepness of the line. The slope is defined as the ratio of the rise to the run of the line.
Using that we substitute the pairs.
(-4,-1), (2,3) would then be (x1, y1), (x2, y2)
The formula to calculate the slope of the line is,
Slope = ( y₂ - y₁ ) / ( x₂ - x₁ )
So you solve from there. the equation would be ( 3 - ( - 1 ) ) / ( 2 - ( - 4 ).
( 3 - ( - 1 ) ) / ( 2 - ( - 4 )
( 3 + 1 ) / ( 2 + 4 )
4 / 6
2 / 3
To know more about slopes follow
https://brainly.com/question/3493733
#SPJ2
A random variable follows a binomial distribution with a probability
of success equal to 0.66. For a sample size of n = 6, find the
values below.
a. the probability of exactly 4 successes
b. the probability of 5 or more successes
c. the probability of exactly 6 successes
d. the expected value of the random variable
Answers
a. The probability of exactly 4 successes is approximately 0.2967.
b. The probability of 5 or more successes is approximately 0.5332.
c. The probability of exactly 6 successes is approximately 0.1399.
d. The expected value of the random variable is 3.96
To solve these problems, we'll use the binomial probability formula:
P(X = k) = C(n, k)× \(p^{k}\)× \((1-p)^{(n-k)}\)
where:
P(X = k) is the probability of getting exactly k successes,
n is the sample size,
p is the probability of success,
C(n, k) is the number of combinations of n items taken k at a time.
Now let's solve each part of the problem:
a. The probability of exactly 4 successes:
P(X = 4) = C(6, 4) × (0.66)⁴ × (1 - 0.66)⁽⁶⁻⁴⁾
C(6, 4) = 6! / (4! × (6 - 4)!) = 6! / (4! × 2!) = (6 × 5) / (2 × 1) = 15
P(X = 4) = 15 × (0.66)⁴ × (0.34)² ≈ 0.2967 (rounded to four decimal places)
b. The probability of 5 or more successes:
P(X ≥ 5) = P(X = 5) + P(X = 6)
P(X = 5) = C(6, 5) × (0.66)⁵ × (1 - 0.66)⁽⁶⁻⁵⁾ = 6 × (0.66)⁵ × (0.34)¹ ≈ 0.3933
P(X = 6) = C(6, 6) × (0.66)⁶ × (1 - 0.66)⁽⁶⁻⁶⁾ = 1 × (0.66)⁶× (0.34)⁰ = 0.1399
P(X ≥ 5) = P(X = 5) + P(X = 6) = 0.3933 + 0.1399 ≈ 0.5332 (rounded to four decimal places)
c. The probability of exactly 6 successes:
P(X = 6) = C(6, 6) × (0.66)⁶ × (1 - 0.66)⁽⁶⁻⁶⁾ = 1 × (0.66)⁶ × (0.34)⁰= 0.1399
d. The expected value of the random variable:
The expected value (mean) of a binomial distribution is given by:
E(X) = n × p
E(X) = 6 × 0.66 = 3.96
Therefore:
a. The probability of exactly 4 successes is approximately 0.2967.
b. The probability of 5 or more successes is approximately 0.5332.
c. The probability of exactly 6 successes is approximately 0.1399.
d. The expected value of the random variable is 3.96
Learn more about binomial distribution here:
https://brainly.com/question/29137961
#SPJ11
can you please help me i need this done!!!

Answers
Answer:
i would say 1.20 is what represents point B
the numbers from $1$ to $150$, inclusive, are placed in a bag and a number is randomly selected from the bag. what is the probability it is neither a perfect square nor a perfect cube? express your answer as a common fraction.
Answers
The required probability is \(\frac{1}{10}\).
This problem is related to probability.
First we have to calculate the number of outcomes and then the number of favorable outcomes.
In this case the numbers are from 1 to 150.
First we have to find the numbers which are perfect square between 1 to 150= {1,4,9,16,25,36,49,64,81,100,121,144}
Now we have to find the numbers which are perfect cube other than those which came in square={8,27,125}
Here the number of favorable outcome is 150 minus number of elements in set of perfect square and perfect cube.
Now the probability of the required problem is = \(\frac{15}{150}\)
= \(\frac{1}{10}\)
To learn more about probability visit the link:
https://brainly.com/question/11234923
#SPJ4
NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. One hundred tickets, numbered 1, 2, 3, . . . , 100, are sold to 100 different people for a drawing. Four different prizes are awarded, including a grand prize (a trip to Tahiti). How many ways are there to award the prizes if it satisfies the given conditions.
Answers
Answer:
a
Step-by-step explanation:
210 oranges, 252 apples and 294 pears are equally packed in cartons so that no fruit is left. What is the biggest possible number of cartons needed?
i also want explanation to pls
Answers
Answer:
∴ The greatest number that divides 210, 252 and 294 is 42.
Step-by-step explanation:
We have to find the LCM of the given rows 12, 15 and 40. (Taking Highest Powers). Therefore, least number of saplings that can be arranged in given rows are 120.
Which of the ratios below is equivalent to 8:5?
Answers
Answer:
Nobody can answer this question if you don't tell us what are the ratios that are 'below'. We have no answers to choose from...