A parallelogram is shown below:

-Photo Below-

Part A: What is the area of the parallelogram? Show your work. (5 points)

Part B: How can you decompose this parallelogram into two triangles? If this parallelogram was decomposed into two triangles, what would be the area of each triangle? (5 points)

The shape of the feasible region is a quadrilateral.

The corner points of the feasible region are as follows:

(0, 6)

(2, 2)

(5, 1)

(10, 0)

To determine the corner points of the feasible region, we can solve the system of inequalities simultaneously.

From the inequality x + y ≥ 6, we have y ≥ 6 - x.

From the inequality 4x + y ≥ 10, we have y ≥ 10 - 4x.

The constraints x ≥ 0 and y ≥ 0 represent non-negativity conditions.

To find the corner points, we need to find the intersection points of the lines defined by the inequalities.

At the intersection of y = 6 - x and y = 10 - 4x, we have:

6 - x = 10 - 4x

3x = 4

x = 4/3

Substituting back into y = 6 - x, we get y = 6 - 4/3 = 14/3.

Therefore, the first corner point is (4/3, 14/3) or approximately (1.33, 4.67).

At the intersection of y = 6 - x and x = 0, we have:

y = 6 - 0

y = 6.

Therefore, the second corner point is (0, 6).

At the intersection of y = 10 - 4x and x = 0, we have:

y = 10 - 4(0)

y = 10.

Therefore, the third corner point is (0, 10).

At the intersection of y = 10 - 4x and y = 0, we have:

0 = 10 - 4x

4x = 10

x = 10/4 = 5/2 = 2.5.

Therefore, the fourth corner point is (2.5, 0).

These four points form the corner points of the feasible region, which is a quadrilateral.

Learn more about shape  from

https://brainly.com/question/25965491

#SPJ11

Since the sequence is always decreasing and cannot go below the lower bound, it becomes increasingly closer to the lower bound, and thus converges to a limit.

A sequence is said to be decreasing if each term is smaller than the previous one, and bounded below if there exists a lower bound such that no term in the sequence is smaller than this bound. In this case, the sequence is decreasing and bounded below by 0.

When a sequence is both decreasing and bounded below, it must have a limit because the terms cannot continue to decrease indefinitely, as they cannot go below the lower bound (in this case, 0). This means that as we progress through the terms of the sequence, the difference between consecutive terms will decrease and eventually approach a constant value.

The limit of a sequence is a value that the terms of the sequence approach as they get closer and closer to the end. In this situation, the limit is the smallest possible value that the sequence can approach, without going below the lower bound.

for such more questions on sequence

https://brainly.com/question/7882626

#SPJ11

Answer:

(0,6) (-2,5) (1,3)

Step-by-step explanation:

The dilation transformation gives an image that is similar to the pre-image but have a different size.

A scale factor is a number that can be used to adjust the size of any geometrical figure or object in relation to its original size. It's used to draw the enlarged or reduced shape of any given figure, as well as to calculate the missing length, area, or volume of an enlarged or reduced figure.

We have,

scale factor = 3

and, centered at (-7, -6).

Points on the figure are; A(-7, -3), B(-3, -2), C(-4, -5)

The given points relative to the center of dilation are;

(-7 - (-7), -3 - (-6)) = (0, 3)

(-3 - (-7), -2 - (-6)) = (4, 4)

(-4 - (-7), -5 - (-6)) = (3, 1)

and, after the dilation is

3 × (0, 3) = (0, 9)

3 × (4, 4) = (12, 12)

3 × (3, 1) = (9, 3)

Adding the coordinates of the center of dilation are

A' = (0 + (-7) , 9 + (-6)) = (-7, 3)

B' = (12 + (-7) , 12 + (-6)) = (5, 6)

C' = (9 + (-7) , 3 + (-6)) = (2, -3)

Therefore, the image is A'(-7, 3), B'(5, 6), C'(2, -3).

Learn more about dilation transformation here:

brainly.com/question/4078841

#SPJ7

See below for the steps to the two-way relative frequency table

The table of values is given as:                                  

Communication Gender  Male         Female    Total

Text                                   150.0           82.0      232.0

Talk                                    72.0            36.0       108.0

Social Media Apps            28.0            32.0      60.0

Total                                   250.0         150.0     400.0

Start by dividing each cell by the column total

                               Male                     Female                  Total

Text                   150.0/250 = 0.6       82.0/150 = 0.55    232/400 = 0.58

Talk                    72.0/250 = 0.288       36.0/150 = 0.24  108/400 = 0.27

Social Media Apps    28.0/250 = 0.112      32.0/150 = 0.21    60/400 = 0.15

Rewrite properly as:

                               Male                Female                  Total

Text                         0.60                0.55                        0.58

Talk                        0.288               0.24                          0.27

Social Media Apps   0.112                0.21                        0.15

Total                             1                       1                              1

The above represents the two-way relative frequency table

Read more about two-way tables at:

https://brainly.com/question/16148316

#SPJ1

The solution to the given linear inequality, 7x - 3(4x - 8) < 6x + 12 - 9x, is x > 6

From the question, we are to solve the given linear inequality for x.

The given inequality is

7x - 3(4x - 8) < 6x + 12 - 9x

Solving the inequality

7x - 3(4x - 8) < 6x + 12 - 9x

Clear the parentheses by applying the distributive property

7x - 12x + 24 < 6x + 12 - 9x

Collect like terms

7x - 12x + 9x - 6x < 12 - 24

Simplify
-2x < -12

Divide both sides by -2 and change the sign

-2x/-2 < -12/-2

x > 6

Hence, the solution is x > 6

Learn more on Solving linear inequalities here: https://brainly.com/question/24372553

#SPJ1

Answer:

Step-by-step explanation:

Answer:

No solution

Step-by-step explanation:

if you distribute the right side of the equation, we get

\(5x + 15 = 5x + 25\)

which is a problem, because this means that

\(5x - 5x = 25 - 15\\0 = 10\\\)

which is a false statement, meaning that no matter what you put into x, the equation will not hold.

hence, there is no solution

Answer:

combination!!

Let's define the following variables:

x = the amount of pure acid (100%) in liters

y = the amount of 20% acid in liters

If mixing the two liquids makes 52 L, then we can say that: (equation1)

In addition, 100% of x liters + 20% of y liters will make 52L of 40% solution then, we can also say that: (equation 2)

Using this two equations, we can solve for the values of x and y using elimination. Here the steps:

1. Subtract equation 2 from equation 1.

2. Divide both sides of the equation by 0.8.

Therefore, the value of y = 39. The amount of 20% acid solution added to the mixture is 39 liters.

3. Plug in the value of y in the equation 1 to solve for x.

The value of x is 13. Hence, the amount of pure acid that was added to the mixture is 13 liters.

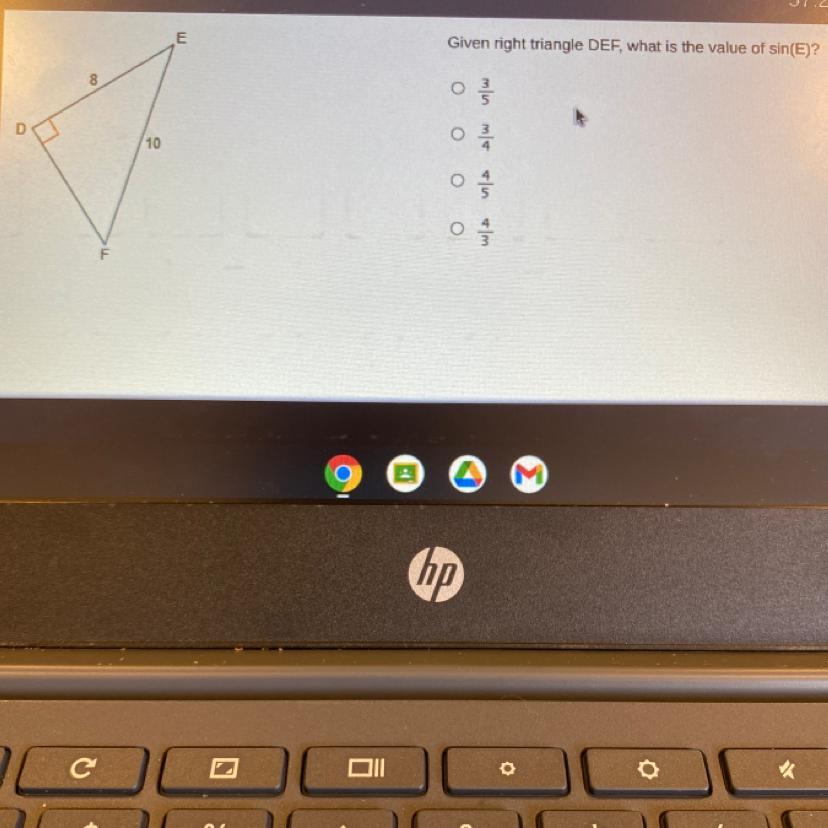
Answer:

sinE = \(\frac{3}{5}\)

Step-by-step explanation:

To find sinE we require DF

Using Pythagoras' identity in the right triangle

DF² = EF² - DE² = 10² - 8² = 100 - 64 = 36 ( take square root of both sides )

DF = \(\sqrt{36}\) = 6

Then

sinE = \(\frac{opposite}{hypotenuse}\) = \(\frac{DF}{EF}\) = \(\frac{6}{10}\) = \(\frac{3}{5}\)

Answer:

\(4x - 27 = - 4x - 35 + 8 \\ 8x = 0 \\ x = 0\)

Answer:

The magnitude is sqrt((-4)^2 + (-9)^2) = 9.85. The angle is atan(-9/-4) = 180 deg + 66 deg = 246 deg = -114 deg.

Step-by-step explanation:

hope it help

Answer:

9.85

Step-by-step explanation:

|v|= √9²+(-4)²

=√81+16

=√97

|v|= 9.85

Answer:The equation of any straight line, called a linear equation, can be written as: y = mx + b, where m is the slope of the line and b is the y-intercept. The y-intercept of this line is the value of y at the point where the line crosses the y axis

Step-by-step explanation:

Answer:

The equation — E = mc2 — means "energy equals mass times the speed of light squared." It shows that energy (E) and mass (m) are interchangeable; they are different forms of the same thing. If mass is somehow totally converted into energy, it also shows how much energy would reside inside that mass: quite a lot.

Step-by-step explanation:

hope this helps..................

Answer:

2

Step-by-step explanation:

-2+4=2

Answer:

Blank 1. -2x+4

Blank 2. x+2

Step-by-step explanation:

Answer:

Step-by-step explanation:

It is actually easier to ignore the left side for now, and work with the right side. The secant function can be represented in terms of cosine by putting a one over cosine. This relation below should be known:

\(sec(x)=\frac{1}{cos(x)}\)

So, if we replace the secants on the right with the above relation, you can make the right side in terms completely of cosine.

\(\frac{1-cos(x)}{1+cos(x)} =\frac{\frac{1}{cos(x)}-1 }{\frac{1}{cos(x)} +1}\)

I hope that's clear to see. Brainly equations are pretty small and blurry.

The next step is to get a common denominator for the right side. The term '1' is equivalent to cos(x)/cos(x). So we have the following:

\(\frac{1-cos(x)}{1+cos(x)} =\frac{\frac{1}{cos(x)}-\frac{cos(x)}{cos(x)} }{\frac{1}{cos(x)} +\frac{cos(x)}{cos(x)} }\)

Looks rather complex, but it simplifies everything by a lot. Combine it into one single fraction:

\(\frac{1-cos(x)}{1+cos(x)} =\frac{\frac{1-cos(x)}{cos(x)} }{\frac{1+cos(x)}{cos(x)} }\)

When you divide by a fraction, it is equivalent to multiplying by the reciprocal. This is an algebra 1 concept, so it should be familiar:

\(\frac{1-cos(x)}{1+cos(x)} =\frac{1-cos(x)}{cos(x)}*\frac{cos(x)}{1+cos(x)}\)

As you can see, the cos(x)'s will cancel, leaving:

\(\frac{1-cos(x)}{1+cos(x)} =\frac{1-cos(x)}{1+cos(x)}\)

QED

By using Gram Schmidt process of orthogonalization, it can be calculated that-

Distance from a vector (2; 3; 1)t to the subspace spanned by the vectors \((1; 2; 3)^T , (1; 3; 1)^T\) IS 2.51 units

What is Gram Schmidt process of orthogonalization?

In an inner product space, the set of mathematical operations which converts a set of linearly independent vectors into an orthonormal vector that spans the same set as spanned by the original vectors is called Gram Schmidt process of orthogonalization.

Distance from \(b=(2,3,1)^T\) to   W= \(Span\left \{u_1= (1,2,3)^T,u_2=(1,3,1)^T \right \}\)

Here, Gram Schmidt process of orthogonalization is used

\(v_1=u_1=(1,2,3)^T\\ v_2=u_2-\frac{ < u_2,v_1 > }{||v_1||^2}v_1\)

     \(=(1,3,1)^T-\frac{(1,2,3)^T.(1,3,1)^T}{(1,2,3)^T.(1,2,3)^T}(1,2,3)^T\\ =(1,3,1)^T-\frac{1+6+3}{1+4+9}(1,2,3)^T\\ =(2/7,11/7,-16/14)^T\)

\(v_2 =(2/7,11/7,-8/7) ^T\)

\(proj_bW=\frac{(2,3,1)(1,2,3)}{(1,2,3)(1,2,3)}(1,2,3)+\frac{(2,3,1)(2/7,11/7,-8/7)}{(2/7,11/7,-8/7)(2/7,11/7,-8/7)}(2/7,11/7,-8/7)\)

             =(1.42, 5.11,  -0.22)

\(b-proj_bW\)=(2,3,1)-(1.42,5.11, -0.22)=(0.58,-2.11,1.22)

Required distance from b onto W=

\(||b-pro_bW||=||(0.58,-2.11,1.22)||=\sqrt{(0.58)^2+(-2.11)^2+(1.22)^2}\) = 2.51 units

To know more about Gram Schmidt process of orthogonalization, refer to the link-

https://brainly.com/question/17412861

#SPJ4

44 kg is equivalent to 97.0078 pounds (lbs).

To convert kilograms (kg) to pounds (lbs), you can use the conversion factor of 2.20462. Multiply the number of kilograms by 2.20462 to get the number of pounds. In this case, 44 kg multiplied by 2.20462 is equal to 97.0078 pounds. It is important to note that this conversion is for the international standard and the formula for conversion may change depending on the countries.

Also, It's important to remember that the pound (lb) and kilogram (kg) are units of weight and should not be confused with mass, which is measured in units such as ounces (oz) and grams (g). In everyday life, weight is more commonly used to measure things like body weight and food weight, while mass is more commonly used in scientific and technical contexts.

To know more about conversion factor  click on the link below:

https://brainly.com/question/30166433#

#SPJ11

Answer:

-45

Step-by-step explanation:

Answer:-45

Step-by-step explanation:

-8-28+(-9)

-8-28-9

calculate the sum of the NEGATIVE NUMBERS

Answer:

28/35 = 4/5

Step-by-step explanation:

28 divided by 7 = 4

35 divided by 7 = 5

Answer:

y = - 7

Step-by-step explanation:

The equation of a horizontal line parallel to the x- axis is

y = c

where c is the value of the y- coordinates the line passes through.

The line passes through (9, - 7 ) with y- coordinate - 7 , then

y = - 7 ← equation of line

Sum of two interiors=exterior

\(\\ \rm\bull\rightarrowtail 2x-3+2x+15=7x-18\)

\(\\ \rm\bull\rightarrowtail 4x+12=7x-18\)

\(\\ \rm\bull\rightarrowtail 3x=30\)

\(\\ \rm\bull\rightarrowtail x=10\)

The answer to part (a) indicates that the ordered pair (0, -2) satisfies the inequality x + y ≤ 2, while the answer to part (b) shows that it does not satisfy the inequality y ≤ (3/2)x - 1.

To explain further, in part (a), the inequality x + y ≤ 2 states that the sum of x and y must be less than or equal to 2. When we substitute the values x = 0 and y = -2 into this inequality, we find that -2 is indeed less than 2, satisfying the inequality. Therefore, the ordered pair (0, -2) is a valid solution for the inequality x + y ≤ 2.

On the other hand, in part (b), the inequality y ≤ (3/2)x - 1 states that y must be less than or equal to (3/2)x - 1. When we substitute the values x = 0 and y = -2 into this inequality, we get -2 ≤ (3/2)(0) - 1, which simplifies to -2 ≤ -1. However, this inequality is not satisfied since -2 is not less than or equal to -1. Therefore, the ordered pair (0, -2) does not satisfy the inequality y ≤ (3/2)x - 1.

In conclusion, the comparison between the answers to parts (a) and (b) shows that the ordered pair (0, -2) can be a solution for one inequality (part a) but not for the other (part b). This demonstrates the importance of evaluating each inequality separately and considering the specific values of x and y to determine their validity.

Learn more about inequality here : brainly.com/question/20383699

#SPJ11

Therefore, the area between the large loop and the small loop of the curve r = 2 + 4cos(3θ) is 70π/3.

To find the area between the large loop and the small loop of the curve, we need to find the points of intersection of the curve with itself.

Setting the equation of the curve equal to itself, we have:

2 + 4cos(3θ) = 2 + 4cos(3(θ + π))

Simplifying and solving for θ, we get:

cos(3θ) = -cos(3θ + 3π)

cos(3θ) + cos(3θ + 3π) = 0

Using the sum to product formula, we get:

2cos(3θ + 3π/2)cos(3π/2) = 0

cos(3θ + 3π/2) = 0

3θ + 3π/2 = π/2, 3π/2, 5π/2, 7π/2, ...

Solving for θ, we get:

θ = -π/6, -π/18, π/6, π/2, 5π/6, 7π/6, 3π/2, 11π/6

We can see that there are two small loops between θ = -π/6 and π/6, and two large loops between θ = π/6 and π/2, and between θ = 5π/6 and 7π/6.

To find the area between the large loop and the small loop, we need to integrate the area between the curve and the x-axis from θ = -π/6 to π/6, and subtract the area between the curve and the x-axis from θ = π/6 to π/2, and from θ = 5π/6 to 7π/6.

Using the formula for the area enclosed by a polar curve, we have:

A = 1/2 ∫[a,b] (r(θ))^2 dθ

where a and b are the angles of intersection.

For the small loops, we have:

A1 = 1/2 ∫[-π/6,π/6] (2 + 4cos(3θ))^2 dθ

Using trigonometric identities, we can simplify this to:

A1 = 1/2 ∫[-π/6,π/6] 20 + 16cos(6θ) + 8cos(3θ) dθ

Evaluating the integral, we get:

A1 = 10π/3

For the large loops, we have:

A2 = 1/2 (∫[π/6,π/2] (2 + 4cos(3θ))^2 dθ + ∫[5π/6,7π/6] (2 + 4cos(3θ))^2 dθ)

Using the same trigonometric identities, we can simplify this to:

A2 = 1/2 (∫[π/6,π/2] 20 + 16cos(6θ) + 8cos(3θ) dθ + ∫[5π/6,7π/6] 20 + 16cos(6θ) + 8cos(3θ) dθ)

Evaluating the integrals, we get:

A2 = 80π/3

Therefore, the area between the large loop and the small loop of the curve r = 2 + 4cos(3θ) is:

A = A2 - A1 = (80π/3) - (10π/3) = 70π/3

To know more about area,

https://brainly.com/question/31479047

#SPJ11

The clock minutes rotate 270 degrees in 45 minutes.

While rotating, the clock's hands are seen to move at a speed of six degrees per minute.

The number of degrees for a clock minute is solved by

60 minutes  = 360 degrees

1 minute = ?

cross multiplying

60 * ? = 360

? = 360 / 60

? = 6

hence 1 minute is 6 degrees

The formula to use to get the calculation is multiplying the number of minutes by 6

Number of degrees in 45 minutes = 45 * 6

Number of degrees in 45 minutes = 270 degrees

Learn more about clock rotation:

brainly.com/question/28741125

#SPJ1

Answer:

B

Step-by-step explanation:

pretty sure im on the same part as u