A pancake recipe calls for 4 1/2 cups of whole wheat flour .If the chef wants to split the recipe into 3 equal batches , how much flour should be in each batch
Answers
Answer: \(1\dfrac12\text{ cups}\)
Step-by-step explanation:
Given : Quantity of flour required for 1 recipe = \(4\dfrac12\) cups
\(=\dfrac{4\times2+1}{2}\) cups
\(=\dfrac92\) cups
Now , if chef wants to split the recipe into 3 equal batches , then quantity of flour in each batch = \(\dfrac92\div 3\) cups
\(=\dfrac92\times\dfrac13\\\\=\dfrac32\text{ cups} = 1\dfrac12\text{ cups}\)
Hence, the quantity of flour in each batch = \(1\dfrac12\text{ cups}\)
Related Questions
Find an equation for the plane consisting of all points that are equidistant from the points (1,0,-2) and (3,4,0).
Answers
The midpoint formula and the normal vector of the plane can be used to determine the equation of the plane that contains all points equidistant from the points (1,0,-2) and (3,4,0).
How is this determined?Given by: The midpoint of the two points is:
M = [(1 + 3)/2, (0 + 4)/2, (-2 + 0)/2] = (2, 2, -1) (2, 2, -1)
The following vector runs between the two points:
V = (3 - 1, 4 - 0, 0 - (-2)) = (2, 4, 2) (2, 4, 2)
The cross product of two non-parallel plane vectors yields the normal vector to the plane. The midpoint M to a point on the plane is one such vector, while the other is the vector V. Consider the point P = (2, 2, -1) + t(2, 4, 2) as an illustration, where t is a scalar.
The normal vector is then provided by:
N = V x (P - M) = (2, 4, 2) x (2t, 4t, 2t -1), which equals (12t, -8t, 4t + 2)
The point-normal form, which makes use of the normal vector N and the point M, can be used to determine the equation for the plane:
(x - 2) * 12t = (y - 2) * -8t = (z + 1) * 4t + 2
The final equation of the plane is obtained by multiplying both sides of the equation by t and setting t 0.
12(x - 2) = -8(y - 2) = 4(z + 1) + 2
Learn more about Coordinate geometry here:
brainly.com/question/18269861
#SPJ4
Origami is the Japanese art of paper folding. The diagram below represents an unfolded paper kabuto, a samurai warrior's helmet. Which of the following are pairs of congruent segments?
Check all that apply.
ANSWER IS C - D - E read your answers carefully A.P.Ex
Answers
The pairs of congruent segments in the diagram are CD, DE, and BC. The concept of congruent segments is a fundamental concept in geometry that is necessary for solving problems and proving.
The diagram shows an unfolded paper kabuto, a samurai warrior's helmet. To identify the pairs of congruent segments, we need to look for segments that have the same length. From the diagram, we can see that segments CD, DE, and BC are all straight lines and appear to have the same length. Therefore, these are the pairs of congruent segments. The length of AB and AE appear to be longer than CD, DE, and BC, so they are not congruent segments. In summary, the pairs of congruent segments in the diagram are CD, DE, and BC.
The concept of congruent segments is important in geometry. Congruent segments are segments that have the same length. In other words, they are identical in size and shape. They are denoted by placing a small line segment above the two segments that are congruent. Congruent segments can be found in various shapes and figures. For instance, in the diagram of the unfolded paper kabuto, we see that segments CD, DE, and BC are congruent segments. Identifying congruent segments is a crucial step in solving geometry problems as it helps in proving congruence between different figures. Congruence is when two shapes have the same size and shape. Therefore, theorems.the concept of congruent segments is a fundamental concept in geometry that is necessary for solving problems and proving.
To know more about congruent segment visit :
https://brainly.com/question/12012957
#SPJ11
(5 points) Suppose that sin 0= -1/4 and that 0 lies in Quadrant IV. Find the value of the other five trigonometric functions at 0.
Answers
The values of the other five trigonometric functions at θ are: cos θ = √15/4, tan θ = -1/√15, csc θ = -4, sec θ = 4/√15, and cot θ = -√15.
Given that sin θ = -1/4 and θ lies in Quadrant IV, we can determine the values of the other trigonometric functions at θ.
To find cos θ, we use the identity cos²θ = 1 - sin²θ. Plugging in the value of sin θ, we get cos²θ = 1 - (-1/4)² = 1 - 1/16 = 15/16. Taking the square root, we get cos θ = √(15/16) = √15/4.
To find tan θ, we use the identity tan θ = sin θ / cos θ. Plugging in the values of sin θ and cos θ, we have tan θ = (-1/4) / (√15/4) = -1/√15.
To find csc θ, we use the identity csc θ = 1 / sin θ. Plugging in the value of sin θ, we get csc θ = 1 / (-1/4) = -4.
To find sec θ, we use the identity sec θ = 1 / cos θ. Plugging in the value of cos θ, we have sec θ = 1 / (√15/4) = 4/√15.
To find cot θ, we use the identity cot θ = 1 / tan θ. Plugging in the value of tan θ, we get cot θ = 1 / (-1/√15) = -√15.
The values of the other five trigonometric functions at θ are:
cos θ = √15/4
tan θ = -1/√15
csc θ = -4
sec θ = 4/√15
cot θ = -√15
To know more about Trigonometric Functions, visit
https://brainly.com/question/25618616
#SPJ11
Show that if U1 and U2 are subspaces of a vector space V, then
dim(U1 + U2) = dim U1 + dim U2 − dim(U1 ∩ U2),
where U1 + U2 is as defined in Exercise 1.5.11.
Hint: Start with a basis of U1 ∩ U2. Extend it to a basis of U1 and a basis of U2, and show that both these bases together form a basis of U1 + U2.
Answers
Let B be a basis for U1 ∩ U2. We will extend B to bases for U1 and U2 and show that the union of these bases is a basis for U1 + U2.
Since U1 and U2 are subspaces of V, they both contain the zero vector. Therefore, B contains the zero vector, and we can extend it to a basis B1 for U1 by adding vectors from U1 that are not in U1 ∩ U2 until we have a basis of U1. Similarly, we can extend B to a basis B2 for U2.
Let B' = B1 ∪ B2. We claim that B' is a basis for U1 + U2.
To prove this, we will show that B' is a linearly independent set that spans U1 + U2.
First, we will show that B' is linearly independent. Suppose that a linear combination of vectors in B' equals the zero vector:
c1v1 + c2v2 + ... + ckvk = 0,
where ci is a scalar and vi is a vector in B'. We need to show that all the ci are zero.
Without loss of generality, assume that v1 is in B1 and v2 is in B2. Since B is a basis for U1 ∩ U2, we can write v1 and v2 as linear combinations of vectors in B:
v1 = a1b1 + a2b2 + ... + ambm,
v2 = b1' + b2' + ... + bn'',
where ai, bi, and bi' are scalars and b1, b2, ..., bm, b1', b2', ..., bn'' are vectors in B.
Therefore, we have:
c1(a1b1 + a2b2 + ... + ambm) + c2(b1' + b2' + ... + bn'') + ... + ckvk = 0.
Since U1 and U2 are subspaces, they are closed under scalar multiplication and vector addition. Thus, the left-hand side of the equation can be rewritten as a linear combination of vectors in B1 and B2:
(c1a1)b1 + (c1a2)b2 + ... + (c2)b1' + (c2)b2' + ... + (ck)vk.
Since B1 and B2 are both bases, they are linearly independent sets. Therefore, all the coefficients in this linear combination must be zero:
c1a1 = 0, c1a2 = 0, ..., c2 = 0, ..., ck = 0.
Since B is linearly independent, we know that a1, a2, ..., am, b1', b2', ..., bn'' are not all zero. Therefore, we must have c1 = c2 = ... = ck = 0, which shows that B' is linearly independent.
Next, we will show that B' spans U1 + U2. Let u be an arbitrary vector in U1 + U2. Then u can be written as a sum of a vector in U1 and a vector in U2:
u = u1 + u2,
where u1 is in U1 and u2 is in U2. Since B1 is a basis for U1, we can write u1 as a linear combination of vectors in B1:
u1 = a1b1 + a2b2 + ... + ambm,
where ai are scalars and b1, b2, ..., bm are vectors in B1. Similarly, we can write u2 as a linear combination of vectors in B2:
u2 = b1' + b2' + ... + bn'',
where bi' are scalars and b1', b2', ..., bn'' are vectors in B2.
Therefore, we have:
u = (a1b1 + a2b2 + ... + ambm) + (b1' + b2' + ... + bn'').
Since U1 and U2 are subspaces, they are closed under vector addition and scalar multiplication. Therefore, the right-hand side of this equation is a linear combination of vectors in B':
u = a1b1 + a2b2 + ... + ambm + b1' + b2' + ... + bn''.
This shows that every vector in U1 + U2 can be expressed as a linear combination of vectors in B'. Therefore, B' spans U1 + U2.
Since we have shown that B' is both linearly independent and spans U1 + U2, it is a basis for U1 + U2. Therefore, we have:
dim(U1 + U2) = |B'| = |B1 ∪ B2|.
To finish the proof, we need to express the dimension of U1 + U2 in terms of the dimensions of U1 and U2 and the dimension of U1 ∩ U2.
Since B is a basis for U1 ∩ U2, it has |B| vectors. We extended B to a basis B1 for U1 by adding |B1| - |B| vectors, and to a basis B2 for U2 by adding |B2| - |B| vectors. Therefore:
|B1| = |B2| = |B| + |B1 ∩ B2|,
where |B1 ∩ B2| is the number of vectors we added to extend B to bases for U1 and U2.
Using this equation, we have:
|B1 ∪ B2| = |B1| + |B2| - |B1 ∩ B2|
= (|B| + |B1 ∩ B2|) + (|B| + |B1 ∩ B2|) - |B1 ∩ B2|
= 2|B| + 2|B1 ∩ B2| - |B1 ∩ B2|
= 2|B| + |B1 ∩ B2|.
Therefore, we have:
dim(U1 + U2) = |B1 ∪ B2| = 2|B| + |B1 ∩ B2|
= 2(dim(U1 ∩ U2)) + dim(U1) - |B| + 2(dim(U1 ∩ U2)) + dim(U2) - |B|
= dim(U1) + dim(U2) - dim(U1 ∩ U2),
as required.
Visit here to learn more about vector brainly.com/question/29740341
#SPJ11
The endpoints of CD are C (4,6) and D(-1, -1). Find the coordinates of the midpoint M.
Coordinates of midpoint M: OO
6
HELP ME PLEASE 20 POINTS
HELP

Answers
Answer:
The answer is
\(( \frac{3}{2} \: , \frac{5}{2} ) \: \: or \: \: (1.5 \: \: , \: \: 2.5)\)Step-by-step explanation:
The midpoint M of two endpoints of a line segment can be found by using the formula
\(M = ( \frac{x1 + x2}{2} \: , \: \frac{y1 + y2}{2} )\)where
(x1 , y1) and (x2 , y2) are the points
From the question the points are
C (4,6) and D(-1, -1)
The coordinates of the midpoint is
\(M = ( \frac{4 - 1}{2} , \: \frac{6 - 1}{2} )\)We have the final answer as
\(( \frac{3}{2} \: , \frac{5}{2} ) \: \: or \: \: (1.5 \: \: , \: \: 2.5)\)Hope this helps you
5/14= h/16. WHAT IS H?
Answers
Answer:
40/7 = h
Step-by-step explanation:
Answer:
x = \(5\frac{5}{7}\)
Step-by-step explanation:
Knowing that ΔBIG ≅ ΔFNS, an angle pair that is NOT necessarily congruent is:
Knowing that ΔDAL ≅ ΔEKS, a side pair that is NOT necessarily congruent is:

Answers
solutions:
1) G ≅ F
2) DA ≅ ES
Explanation:
Q)1
ΔBIG ≅ ΔFNS
pairs that are congruent:
B ≅ FI ≅ NG ≅ SFrom the list given,
→ G ≅ F is not necessarily congruent.
Q)2
ΔDAL ≅ ΔEKS
pairs that are congruent:
DA ≅ EKAL ≅ KSDL ≅ ESFrom the list given,
DA ≅ ES is not necessarily congruent.
Usually the congruence is done according to naming
So
∆BIG≅∆FNS<B=F
<I=<N
<G=<S
Option A#2
Check the naming
∆DAL≅∆EKSSo
DA=EK
And DA may not be equal to ESSo option D
A multiple of 18 that is also a square numbers
Answers
3^8 x 2^3 divided by 3^5
Answers
Answer:
216
HOPE THIS HELPS
PLS GIVE BRAINLIEST
Find a formula for the exponential function passing through thepoints (-1, 2/5 ) and (3,250)
Answers
The exponential function between (-1, 2/5) and (3, 250) is as follows:
\(f(x) = 2 * 5^x\)
By combining the fourth roots from both sides, we arrive at:
b = 5
When we use the expression we discovered for a and this value of b, we get:
a = (2/5) * 5 = 2
As a result, the exponential function between (-1, 2/5) and (3, 250) is as follows:
\(f(x) = 2 * 5^x\)
what are functions?A relation between a collection of inputs and outputs is known as a function. A function is, to put it simply, a relationship between inputs in which each input is connected to precisely one output. Each function has a range, codomain, and domain. The usual way to refer to a function is as f(x), where x is the input. A function is typically represented as y = f. (x).
In mathematics, a function is a unique arrangement of the inputs (also referred to as the domain) and their outputs (sometimes referred to as the codomain), where each input has exactly one output and the output can be linked to its input.
from the question:
This is the shape of the exponential function:
f(x) = a *\(b^x\)
where a represents the starting point and b represents the exponential function's base.
We must solve the system of equations to determine the values of a and b that meet the requirements:
a * \(b^(-1)\) = 2/5 (equation 1)
a *\(b^3\)= 250 (equation 2)
We can solve for an in equation 1 by multiplying both sides by b:
a = (2/5) * b
Substituting this expression into equation 2, we get:
(2/5) * b *\(b^3\) = 250
Simplifying, we get:
\(b^4 = 3125\)
By combining the fourth roots from both sides, we arrive at:
b = 5
When we use the expression we discovered for a and this value of b, we get:
a = (2/5) * 5 = 2
As a result, the exponential function between (-1, 2/5) and (3, 250) is as follows:
\(f(x) = 2 * 5^x\)
to know more about functions visit:
https://brainly.com/question/12431044
#SPJ1
which is the best measure of central tendency for the data set below? { 10, 18, 13, 11, 62, 12, 17, 15}
Answers
To determine the best measure of central tendency for the given data set {10, 18, 13, 11, 62, 12, 17, 15}, we typically consider three measures: the mean, median, and mode. Let's calculate each measure and assess which one is most appropriate.
1. Mean: The mean is calculated by summing all the values in the data set and dividing by the total number of values. For this data set:
Mean = (10 + 18 + 13 + 11 + 62 + 12 + 17 + 15) / 8 = 15.5
2. Median: The median is the middle value when the data set is arranged in ascending or descending order. If there are two middle values, the median is the average of those values. First, let's sort the data set in ascending order: {10, 11, 12, 13, 15, 17, 18, 62}. Since there are 8 values, the median is the average of the 4th and 5th values: (13 + 15) / 2 = 14.
3. Mode: The mode is the value that appears most frequently in the data set. In this case, there is no value that appears more than once, so there is no mode.
Considering the data set {10, 18, 13, 11, 62, 12, 17, 15}, we have the following measures of central tendency:
Mean = 15.5
Median = 14
Mode = N/A (no mode)
To determine the best measure of central tendency, it depends on the specific context and purpose of the analysis. If the data set is not heavily skewed or does not contain extreme outliers, the mean and median can provide a good representation of the data. However, if the data set is skewed or contains outliers, the median may be a more robust measure. Ultimately, the best measure of central tendency would be determined by the specific requirements of the analysis or the nature of the data set.
To know more about outliers visit-
brainly.com/question/13054469
#SPJ11
Triangles ABC and DEF are similar. If ∠ABC = 101°and ∠BCA = 39°, find the measure of angle FDE.
Answers
Two triangles, ABC and DEF, similar. <ABC = 101° and <BCA = 39°. Find the angle of FDE!
40°
EXPLANATIONKnown :Triangle ABC and DEF is similar<ABC = 101° = <DEF<BCA = 39° = <DFEAsked :Angle of FDEAnswer :
The sum of all triangle angle is 180°
101 + 39 = 140°
180 - 140 = 40°
So, the angle of FDE is 40°
ANSWER DETAILSSubject : Math
Class : 7th Grade (Junior High School)
Chapter : -
Categorization Code : -
Keywords : Angle of a triangle
Does anyone know how to do this?
Find the value of each variable

Answers
Answer:
a = 37°
b = 34°
c = 143°
Step-by-step explanation:
Hello!
The measure of Angle A is 37°, because 37° and Angle A are vertical angles, meaning they are equal in measure.
Vertical Angles are the non-adjacent angles formed by the intersection of two lines, and are equal in measure.
The measure of Angle C is 143°, found by subtracting 37° from 180°, the total number of degrees on a line.
The measure of Angle B is 34°, found by subtracting 109° and 37° from 180°. Angle B is inside a triangle, and the sum of angles in a triangle is 180°. The other two angles are 109° and 37° (Angle A), so the measure of Angle B should be 34°.
(a) An angle measures 28°. What is the measure of its complement?
(b) An angle measures 132°. What is the measure of its supplement?
Answers
Complementary angles has sum of \(90^{o}\) and supplementary angles have sum of \(180^{o}\) , The answer is \(62^{o}\) and \(48^{o}\) .
What do you mean by angle?When two straight lines or rays intersect at a single endpoint, an angle is created. The vertex of an angle is the location where two points come together.
What is complementary and supplementary angle?When two angles' measurements add up to 90 degrees, they are said to be complementary. When two angles' measures sum up to 180 degrees, they are said to be supplementary. Keeping in mind that the letter s follows the letter c in the alphabet and that 180 is greater than 90 can help you avoid conflating these definitions.
\(28^{o}\)
complement = \(90^{o}-28^{o}\) = \(62^{o}\)
\(132^{o}\)
supplement= \(180^{o}-132^{o}\) = \(48^{o}\)
To learn more about angles visit:
https://brainly.com/question/14569348
#SPJ1
si el total es 153 cual seriael pocentajje de 107?
Answers
If the total is 153, then the percentage would be of 107 be simply calculated by using the formula as 69.935.
The denominator of a percentage (also known as a ratio or fraction) is always 100. Sam, for instance, would have received 30 out of a possible 100 points if he had received 30% on his maths test. In ratio form, it is expressed as 30:100 and in fraction form as 30/100. In this case, the percentage symbol "%" is interpreted as "percent" or "percentage."
This percent sign may always be changed to a fraction or decimal equivalent by using "divided by 100."
We already have our first value 153 and the second value 107. Let's assume the unknown value is Y which answer we will find out.
As we have all the required values we need, Now we can put them in a simple mathematical formula as below:
STEP 1
Y = 107 / 153
By multiplying both numerator and denominator by 100 we will get:
STEP 2
Y = 107 /153 × 100
= 69.935
STEP 3
Y = 69.935
Finally, we have found the value of Y which is 69.935 and that is our answer.
Learn more about Percentages:
https://brainly.com/question/16563240
#SPJ4
Complete question;
If the total is 153, what would be the percentage of 107?
Rational number between 3.623623 and 0.484848
Answers
Answer:
1
Step-by-step explanation:
A rational number between 3.623623 and 0.484848 is 1.
Answer:
Remember: rational numbers are numbers that can be written as fractions and decimals that either terminate or repeat. Here are some rational numbers:
0.5, 3/4, 1, 1.5...3, 3.5
Step-by-step explanation:
BRAINLIEST, PLEASE!
Draw a picture and label it. Set up an equation and solve it. Show all your work. Round an angle to the nearest tenth of a degree. Roundthe length of a side to the nearest hundredth of a unit.A television transmitter tower is 600 feet high. If the angle between the guy wire (attached at the top) and the tower is 59.2º, how longis the guy wire?

Answers
see the attached figure below to better understand the problem
we have that
cos(59.2)=600/L
Solve for L
L=600/cos(59.2)
L=1,171.78 ft
therefore
the answer is 1,171.78 ft
What is the value of x in the equation 8x – 2y = 48, when y = 4?
Answers
Answer:
x = 7
Step-by-step explanation:
since we know y = 4, we can plug this into the equation to find x
8x - 2y = 48
8x - 2(4) = 48
8x - 8 = 48
8x = 56
x = 7
Answer:
x=7
Step-by-step explanation:
8x – 2y = 48
Let y=4
8x - 2(4) = 48
8x - 8 = 48
Add 8 to each side
8x -8+8 = 48+8
8x = 56
Divide each side by 8
8x/8 = 56/8
x = 7
Need this in C. Provided is a sample output for the function needed below. Just need it to add two vectors magnitude and direction and output calculated magnitude and direction- add The add command will be followed by a set of 4 integers. They are pairs of magnitudes and directions for two vectors. This command will compute the magnitudes and directions for resultant vector. Tabs separate the integers. The line will have the format: add −3.60699
−21.82220
22.11829
260.61445
Answers
The `M_PI` constant is used from the `math.h` library to convert between degrees and radians. The `%lf` format specifier is used with `scanf` to read double precision floating-point values.
To calculate the magnitude and direction of the resultant vector obtained by adding two vectors, you can use the following C code:
```c
#include <stdio.h>
#include <math.h>
void add_vectors(double mag1, double dir1, double mag2, double dir2, double *res_mag, double *res_dir) {
double x1 = mag1 * cos(dir1 * M_PI / 180.0); // Convert degrees to radians
double y1 = mag1 * sin(dir1 * M_PI / 180.0);
double x2 = mag2 * cos(dir2 * M_PI / 180.0);
double y2 = mag2 * sin(dir2 * M_PI / 180.0);
double res_x = x1 + x2;
double res_y = y1 + y2;
*res_mag = sqrt(res_x * res_x + res_y * res_y); // Calculate magnitude using Pythagorean theorem
*res_dir = atan2(res_y, res_x) * 180.0 / M_PI; // Convert radians to degrees
}
int main() {
double mag1, dir1, mag2, dir2, res_mag, res_dir;
printf("Enter the magnitude and direction of the first vector (separated by a space): ");
scanf("%lf %lf", &mag1, &dir1);
printf("Enter the magnitude and direction of the second vector (separated by a space): ");
scanf("%lf %lf", &mag2, &dir2);
add_vectors(mag1, dir1, mag2, dir2, &res_mag, &res_dir);
printf("The magnitude of the resultant vector is %.5f\n", res_mag);
printf("The direction of the resultant vector is %.5f\n", res_dir);
return 0;
}
```
This code defines a function `add_vectors` that takes the magnitudes and directions of two vectors as input, and calculates the magnitude and direction of the resultant vector. It then uses the `scanf` function to read the inputs from the user, calls the `add_vectors` function, and finally prints the calculated magnitude and direction of the resultant vector.
The `add_vectors` function performs vector addition by converting the magnitudes and directions into Cartesian coordinates. It then adds the corresponding components, calculates the magnitude using the Pythagorean theorem, and determines the direction using the `atan2` function. The results are stored in the variables pointed to by `res_mag` and `res_dir`.
Note that the `M_PI` constant is used from the `math.h` library to convert between degrees and radians. The `%lf` format specifier is used with `scanf` to read double precision floating-point values.
Learn more about radians here
https://brainly.com/question/30984313
#SPJ11
A cone has volume 525 cm . What is the volume of a cylinder with the same radius and height?
Answers
Answer:
1,575 cm³
Step-by-step explanation:
If r is the radius of a cone and h is its height, the volume of the cone is
(1/3)πr²h
The volume of a cylinder with same radius r and same height h is πr²h
So the volume of a cylinder with same radius and height as a cone will be 3 x volume of cone
Here volume of cone = 525 cm³
volume of cylinder = 3 x 525 = 1,575 cm³
solve the linear equation 1/5(10x-20)=x-3
Answers
Answer:
x=1
Step-by-step explanation:
1/5(10x-20)=x-3
2x-4=x-3
2x-x=4-3
x=1
Answer:
The value of x is 1 after solving the linear equation.
Step-by-step explanation:
Given equation is:
\(\frac{1}{5}(10x-20)=x-3\)
We will solve the equation by simplifying first.
\(\frac{1}{5}*10x-\frac{1}{5}*{20}=x-3\\2x-4=x-3\)
Now, we will subtract x from both sides of the equation,
2x-x-4 = x-x-3
x-4 = -3
Next, we will add 4 on the both sides of the equation,
x-4+4 = -3+4
x = 1
Hence,
The value of x is 1 after solving the linear equation.
Help Needed!! Find The Value Of X (Geometry)

Answers
Give an example of a function that is a dilation and a reflection of the parent function.
Answers
Answer: f(x) = -1/2(x+3)
Example: g(x) = -1/2(-x-3)
This function is a dilation and a reflection of the parent function f(x) because when graphed, the two functions have the same shape but are reflected over the y-axis and are half the size of the original.
The area of triangle xyz is 35 cm. the height is 10cm. what is the base of the triangle?
Answers
35=1/2(10 x b)
35=5 x b
35=5b
7cm=b is the base of the triangle
Answer:
Base of the triangle = 7 cm
Step-by-step explanation:
Given information,
→ Area of triangle = 35 cm
→ Height = 10 cm
Now we have to,
→ Find the base of the triangle.
Formula we use,
→ Area = ½ × b × h
Forming the equation,
→ (1/2) × b × 10 = 35
Then the value of b will be,
→ (1/2) × b × 10 = 35
→ (b × 10)/2 = 35
→ 10b/2 = 35
→ 10b = 35 × 2
→ 10b = 70
→ b = 70/10
→ [ b = 7 cm ]
Hence, the value of b is 7 cm.
Find the area of the shaded region.

Answers
Answer:
10pix+65pi
Step-by-step explanation:
pi(x+9)^2-pi(x+4)^2
=pi(x^2+18x+81)-pi(x^2+8x+16)
=pix^2+18pix+81pi-pi(x^2+8x+16)
=pix^2+18pix+81pi-pix^2-8pix-16pi
=10pix+65pi
Figure P was rotated about the origin (0,0) by 90 degrees counterclockwise.
Which figure is the image of P?

Answers
The figure that represents the image of P is given as follows:
Figure A.
What are the rotation rules?The rotation rules are defined as follows:
90° clockwise rotation: (x,y) -> (y,-x)90° counterclockwise rotation: (x,y) -> (-y,x)180° clockwise and counterclockwise rotation: (x, y) -> (-x,-y)270° clockwise rotation: (x,y) -> (-y,x)270° counterclockwise rotation: (x,y) -> (y,-x)The vertices of figure P are given as follows:
(-2, -2), (-6,-2) and (-3,-7).
The rule for a rotation of 90º degrees counterclockwise about the origin is given as follows:
(x,y) -> (-y,x).
Meaning that the vertices of the image of P are given as follows:
(2,-2), (2,-6) and (7,-3).
Meaning that Figure A is the image of P.
More can be learned about rotation rules at brainly.com/question/17042921
#SPJ1
11. Use the geometric series and differentiation to find a power series representation for the function () xin(1 + x) 12. Find a Taylor series for f(x) = 3* centered at a=1 and find its radius of convergence 13. Use the Maclaurin series cos x to evaluate the following integral as a power series. [cos Viax
Answers
In question 11, the geometric series and differentiation are used to find a power series representation for the function f(x) = x/(1 + x). In question 12, a Taylor series for f(x) = 3* is found centered at a = 1, and the radius of convergence is determined. In question 13, the Maclaurin series for cos(x) is used to evaluate the integral ∫cos(x) dx.
11. To find a power series representation for f(x) = x/(1 + x), we can rewrite the function as f(x) = x * (1/(1 + x)). Using the formula for the geometric series, we have 1/(1 + x) = 1 - x + x^2 - x^3 + ..., which converges for |x| < 1. Now, we differentiate both sides of the equation to find the power series representation for f(x):
f'(x) = (1 - x + x^2 - x^3 + ...)'
Applying the power rule for differentiation, we get:
f'(x) = 1 - 2x + 3x^2 - 4x^3 + ...
Thus, the power series representation for f(x) = x/(1 + x) is given by:
f(x) = x * (1 - 2x + 3x^2 - 4x^3 + ...)
12. To find the Taylor series for f(x) = 3* centered at a = 1, we can start with the Maclaurin series for f(x) = 3* and replace every instance of x with (x - a). In this case, a = 1, so we have:
f(x) = 3* = 3 + 0(x - 1) + 0(x - 1)^2 + ...
Therefore, the Taylor series for f(x) = 3* centered at a = 1 is:
f(x) = 3 + 0(x - 1) + 0(x - 1)^2 + ...
The radius of convergence of this series is infinite, since the terms are all zero except for the constant term.
13. The Maclaurin series for cos(x) is given by:
cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...
To evaluate the integral ∫cos(x) dx as a power series, we can integrate each term of the series:
∫cos(x) dx = ∫(1 - x^2/2! + x^4/4! - x^6/6! + ...) dx
Integrating term by term, we get:
∫cos(x) dx = x - x^3/(32!) + x^5/(54!) - x^7/(7*6!) + ...
This gives us the power series representation of the integral of cos(x) as:
∫cos(x) dx = x - x^3/(32!) + x^5/(54!) - x^7/(7*6!) + ...
The radius of convergence of this series is also infinite, since the terms involve only powers of x and the factorials in the denominators grow rapidly.
Learn more about geometric series here:
https://brainly.com/question/30264021
#SPJ11
write an equation for the line parallel to y 3x - 8 through the point (-2,-7)
Answers
Answer:
y = 3x - 1
Step-by-step explanation:
In order for lines to be parallel, they must have the same slope.
The slope of y = 3x - 8 is 3.
Now, we can solve it using point-slope form. Remember that m = 3, x₁ = -2 and y₁ = -7:
y − y₁ = m(x − x₁)
y - (-7) = 3(x - (-2))
y + 7 = 3(x + 2)
Distribute 3 and isolate y:
y + 7 = 3x + 6
y = 3x - 1
Find the solution of the differential equation that satisfies the given initial condition.
dy/dx = x/y, y(0) = -2
Answers
The solution to the given differential equation as required is; y = √(x² + 4).
What is the solution to the given differential equation?As evident in the task content;
dy / dx = x / y, y(0) = -2
Therefore, we have that;
dy (y) = dx (x)
By integration of both sides indefinitely;
y² / 2 = x²/2 + C
y² = x² + 2c
y = √(x² + 2c)
Hence, using the initial conditions;
-2 = √(0² + 2c)
-2 = √2c
2c = 4
c = 2.
Hence, the required solution of the differential equation as given is; y = √(x² + 4) since c = 2.
Read more on variable separable differential equations;
https://brainly.com/question/30490090
#SPJ1
can you help me can you help me
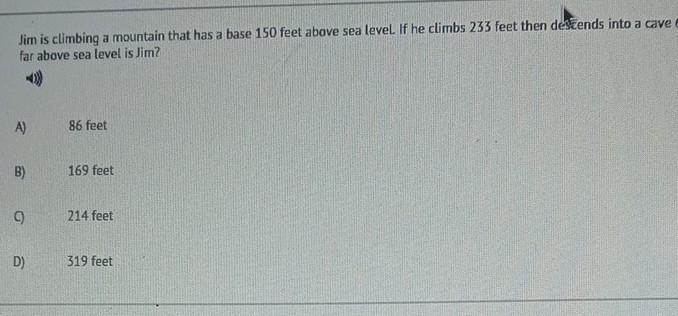
Answers
Answer: a
Ftftrcrcrwftdvtsvdtsvgxvsgvxtsvxt
Answer:
The mountain has a base 150 feet above sea level.
Jim climbs 233 feet
150 + 233 = 383 feet above sea level.
After that, he descends x feet, but the picture is cropped.