a modle kit contains curved tracks and straight given that 35% of the tracks are curved what fraction of the tracks are straight write this fraction in simplest form
Answers
The fraction of tracks that are straight in the model kit is 13/20, in simplest form.
To find the fraction of tracks that are straight in the model kit, we need to subtract the fraction of curved tracks from 1 (since the total fraction of tracks should equal 1).
Given that 35% of the tracks are curved, we can express this as a fraction by dividing 35 by 100:
Fraction of curved tracks = 35/100 = 7/20
To find the fraction of straight tracks, we subtract the fraction of curved tracks from 1:
Fraction of straight tracks = 1 - 7/20
To subtract fractions, we need a common denominator. In this case, the common denominator is 20:
Fraction of straight tracks = 20/20 - 7/20
Fraction of straight tracks = 13/20
Therefore, the fraction of tracks that are straight in the model kit is 13/20, in simplest form.
Learn more about fraction here
https://brainly.com/question/30154928
#SPJ11
Related Questions
HELP ASAP!
Kurt and Maria’s high school is having a newspaper drive.The goal is to collect 3,585 pounds of newspapers. So far, 21% of the goal has been reached.
Kurt estimated the number of pounds of newspapers collected by finding 10% of 3,600 and then multiplying the result by 2.
Maria estimated the number of pounds of newspapers collected by finding One-fifth of 3,600.
Who is right, and why?
Neither Kurt nor Maria is right, because 3,500 should be used instead of 3,600.
Kurt is right, because finding One-fifth of 3,600 is not a good way to approximate 21% of 3,585.
Maria is right, because finding 10% of 3,600 and multiplying the result by 2 is not a good way to approximate 21% of 3,585.
Both Kurt and Maria are right, because 3,585 should be rounded up to 3,600, and 21% of this amount can be approximated by either finding 10% of 3,600 and multiplying the result by 2 or by finding One-fifth of 3,600.
Answers
D. Both Kurt and Maria are right, because 3,585 should be rounded up to 3,600, and 21% of this amount can be approximated by either finding 10% of 3,600 and multiplying the result by 2 or by finding 1/5 of 3,600.
Answer:
Both Kurt and Maria are right, because 3,585 should be rounded up to 3,600, and 21% of this amount can be approximated by either finding 10% of 3,600 and multiplying the result by 2 or by finding 1/5 of 3,600.
Step-by-step explanation:
Emma pays $2,600 for a washer/dryer combo. Each year, the appliance loses 15% of its resale value. How much will it be worth in 4 years?
If necessary, round your answer to the nearest cent.
Answers
The value for the washer/dryer combo after 4 years is 1,357.2 dollars.
How much will it be worth in 4 years?We know that Emma pays $2,600 for a washer/dryer combo. Each year, the appliance loses 15% of its resale value, then the value after x years is modeled by the exponential decay.
V(x) = 2,600*(1 - 0.15)ˣ
The value after 4 years is what we get when we evaluate this in x = 4, we will get:
V(4) = 2,600*(1 - 0.15)⁴
Simplify that:
V(4) = 1,357.2
The value is after 4 years of the washer/dryer is 1,357.2 dollars.
Learn more about exponential decays at:
https://brainly.com/question/27822382
#SPJ1
Rita plans to make a call using a calling card. For each call, rita has two options: 1. Pay $0. 49, plus an additional $0. 019 per minute. 2. Pay $0. 059 per minute. She predicts that her call will be x minutes long. Which inequality represents the statement, "rita would save money using the second option"?.
Answers
The inequality that represents Rita saving money from the second option is 0.059x < 0.49 + 0.019x
"Information available from the question"
In the question:
1. Pay $0. 49, plus an additional $0. 019 per minute.
2. Pay $0. 059 per minute.
Now, According to the question:
How to determine the inequality that represents the statement?
We have the following parameters that can be used in our computation:
1. Pay $0.49, plus an additional $0.019 per minute.
2. Pay $0.059 per minute.
These statements can be represented as
Option 1: y = 0.49 + 0.019x
Option 2: y = 0.059x
Where y is the total amount and x is the number of minutes
When she saves money, we have
Option 2 < Option 1
Substitute the known values in the above equation, so, we have the following representation
0.059x < 0.49 + 0.019x.
Learn more about Inequality at:
https://brainly.com/question/27989101
#SPJ4
Amy cut 32 feet of chain into pieces that were each
1
4
ft long. How many of these pieces did Amy have after cutting the chain?
Be sure to use the correct place value.
Answers
Answer:
32ft of chain divided by 14ft pieces... that's two pieces of chain
Step-by-step explanation:
Answer:
2
Step-by-step explanation:
32÷14=2.2857
2 with a remainder of 4feet
70% of boys who were surveyed at the school love to play videogames. 84 boys said they did not like to play videogames. How many boys were surveyed?
Answers
There are 84 boys said they did not like to play videogames. There are total 150 boys were surveyed.
The union of two sets A and B is the set of all elements of A or B, i.e. A ∪ B, while the intersection of two sets A and B is the set of all common elements. The intersection of these two sets is denoted A ∩ B.
According to the Question:
n(videogame) = 70
n(not videogame) = 84
n(total number of boy surveyed) =?
n(total number of boy surveyed) = n(videogame) + n(not videogame)
= 84 + 70
= 150
Therefore, there are total 150 boys who are surveyed.
Learn more about Boys:
https://brainly.com/question/22633296
#SPJ4
Brian pays £475.29 a year on his car insurance. The insurance company reduces the price by 2.1%.
How much does the insurance cost now?
Give your answer rounded to 2 DP.
Answers
Answer:
470.12??? not sure!!!!
Step-by-step explanation:
A company sells widgets. The amount of profit, y, made by the company, is the selling price of each widget, x, by the given equation. Using this equation, find out what price the widgets should be sold for, to the nearest cent, for the company to make the maximum profit. y = -x^2+ 101x – 900
Answers
We want maximum profit, which is the max value of y.
We basically want for which x value, we have y as the maximum.
First,
let's take the derivative of y:
\(\begin{gathered} y=-x^2+101x-900 \\ y^{\prime}=-2x+101 \end{gathered}\)Maximum is when the derivative is equal to 0. So, the x-value when derivative is 0:
\(\begin{gathered} y^{\prime}=-2x+101 \\ 0=-2x+101 \\ 2x=101 \\ x=\frac{101}{2} \\ x=50.5 \end{gathered}\)To get max profit, the widgets should be sold at $50.50
Which of the following is equivalent to 8?
3 to the power of 2
2 to the power of 4
2 to the power of 3
4 to the power of 2
Answers

Write the following phrase
as an
inequality: 3 more than twice n is at most 50.
Answers
Step-by-step explanation:
3 more than twice n = 3+2n
3 more than twice n is atmost 50,
=> 3+2n <= 50 {(3+2n) is less than or equal to 50}
Answer:
3 + 2n ≤ 50
Step-by-step explanation:
"at most 50" means 50 or less.
Hope this helps.
Hurry I need it now!
(04.01 MC)
Quadrilateral ABCD has coordinates. MA (3, 1), B (4, 4), C (7, 5), D (6, 2). Quadrilateral ABCD is?
Answers
Answer:
c
Step-by-step explanation:
i just took a test
a manufacturer wishes to set a standard time required by employees to complete a certain process. times from 21 employees have a mean of 6 hours and a standard deviation of 2 hours. test if the mean processing time exceeds 5.5 hours. what is the -value of the test (round off to second decimal place)? assume normal population.
Answers
The -value of the test is 1.90. This indicates that the mean processing time is significantly greater than 5.5 hours, supporting the manufacturer's desire to set a standard time required by employees to complete a certain process
The t-value will be equal to 1.39 for the given statistics.
How to calculate the t-value?To test if the mean processing time exceeds 5.5 hours, we can use a one-sample t-test.
The null hypothesis is that the mean processing time is less than or equal to 5.5 hours:
H0: µ ≤ 5.5
The alternative hypothesis is that the mean processing time is greater than 5.5 hours:
Ha: µ > 5.5
We will use a significance level of 0.05.
The formula for the t-test statistic is:
t = (X - µ) / (s / √n)
Where:
X = sample mean
µ = hypothesized population mean
s = sample standard deviation
n = sample size
Substituting the given values, we get:
t = (6 - 5.5) / (2 / √21) = 1.386
The degree of freedom for the t-test is n-1 = 20.
Using a t-table or calculator, the p-value associated with a t-value of 1.386 and 20 degrees of freedom is 0.093.
Since the p-value (0.093) is greater than the significance level (0.05), we fail to reject the null hypothesis. Therefore, there is not enough evidence to suggest that the mean processing time exceeds 5.5 hours.
To know more about t-value follow
https://brainly.com/question/22848147
#SPJ2
Find the missing partial products of 2.8x4.6
Answers
Answer:
the answer is 12.88
Step-by-step explanation:
Answer:
The answer to your question is 12.88
Step-by-step explanation:
39. Solve for x. Justify your answer

Answers
Answer:
x=50 degrees
Step-by-step explanation:
this is a straight angle which is 180 degrees.
we know one angle is 25
so 3x+5=155
using algebra
3x=150
x=50
hope that helps =)
Answer:
x=50 degrees
Step-by-step explanation:
hope this helps:)
True or false: Under appropriate circumstances, many discrete random variables can be described by the normal distribution.
Answers
True. Under appropriate circumstances, many discrete random variables can be described by the normal distribution.
Under appropriate circumstances, many discrete random variables can be approximated by the normal distribution using the Central Limit Theorem. This theorem states that the sum of a large number of independent and identically distributed random variables, regardless of their individual distributions, tends to follow a normal distribution.
This is often the case in practice, making the normal distribution a useful tool for modeling and analyzing data. However, it's important to note that not all discrete random variables can be accurately described by the normal distribution, and it's important to assess the appropriateness of the normal approximation on a case-by-case basis.
learn more about " normal distribution":-https://brainly.com/question/4079902
#SPJ11
ANSWER ASAP A basketball team played six games. In those games, the team won by 8 points, lost by 8, won by 7, won by 10, lost by 2, and won by 9. What was the mean difference in game scores over the six games?
Answers
The average difference or mean in game scores across six games is 5.67
MeanThe mean is the average of a data set. The mode is the most common number in a data set. The median is the middle of the set of numbers. The mean is the average or the most common value in a collection of numbers. the mean is one of the measures of b, apart from the mode and median. Mean is nothing but the average of the given set of a data.
To solve this problem, we have to write the wins and loss separate and then find the mean.
Wins = 8 points, 7 points, 20 points, 9 points
Loss = 8 points, 2 points
The sum of win points = 8 + 7 + 20 + 9 = 44 points
The sum of lost points = 8 + 2 = 10 points
The mean difference = (win - loss)/ total number of games
The mean difference = ( 44 - 10) / 6
The mean difference = 34 / 6 =5.67
The mean difference in the game scores over six games is 5.67 points
Learn more on mean here;
https://brainly.com/question/1136789
#SPJ1
Let f be a continuous function on the closed interval [0, 2] . If 2 ≤ f(x) ≤ 4, then the greatest
possible value of (integral from 0 to 2)f(x)dx is
a. 0
b. 2
c. 4
d. 8
e. 16
Answers
The correct answer is d. 8, as it represents the greatest possible value for the integral of f(x) over the interval [0, 2].
Given that 2 ≤ f(x) ≤ 4 for all x in the interval [0, 2], we know that the function f(x) is bounded between 2 and 4 throughout the interval. To find the greatest possible value of the integral of f(x) over the interval [0, 2], we want to maximize the area bounded by the function and the x-axis.
Since the function is continuous and bounded, we can use the Fundamental Theorem of Calculus to find the integral. The integral of f(x) over the interval [0, 2] represents the area under the curve of f(x) between x = 0 and x = 2.
The maximum possible value of this integral occurs when the function is at its upper bound of 4 throughout the interval. Therefore, the greatest possible value of the integral is the area of the rectangle with a base of 2 (the width of the interval) and a height of 4, which is 2 * 4 = 8.
Hence, the correct answer is d. 8, as it represents the greatest possible value for the integral of f(x) over the interval [0, 2].
To know more about integral refer here:
https://brainly.com/question/31433890
#SPJ11
Someone help please. (The teacher added an extra question for some reason but please help with all.)
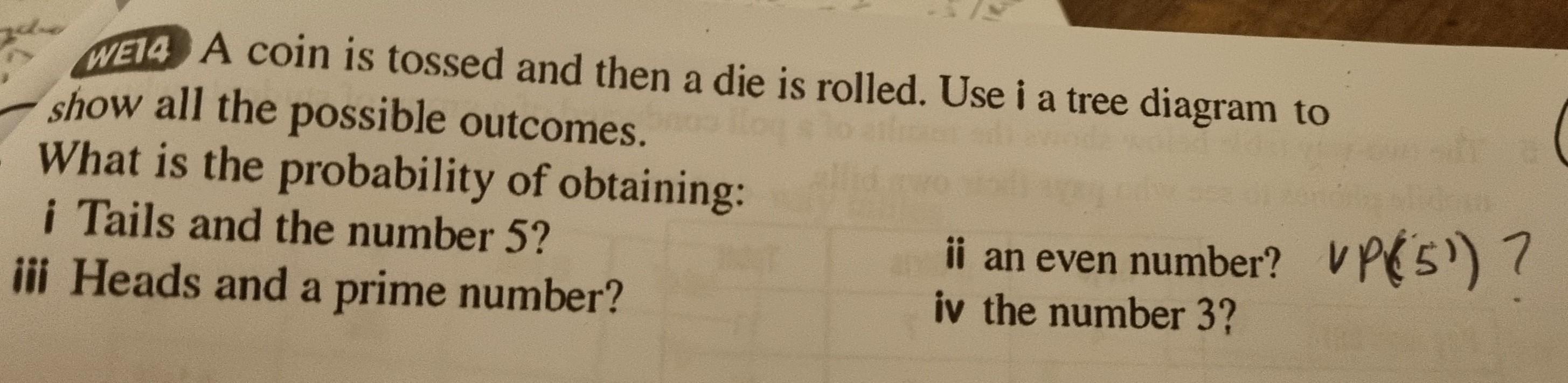
Answers
The probability of obtaining tails and the number 5 is 1/12
the probability of obtaining an even number is 1/2
P(heads and prime number) 1/4
How to calculate the probabilitySince the events are independent, the probability of obtaining tails and the number 5 is:
P(tails and 5) = P(tails) * P(5) = (1/2) * (1/6) = 1/12
The coin toss outcome is irrelevant, so the probability of obtaining an even number is:
P(even number) = 1/2
The probability of obtaining heads and a prime number is:
P(heads and prime number) = P(heads) * P(prime number) = (1/2) * (1/2) = 1/4
Learn more about probability on
https://brainly.com/question/24756209
#SPJ1
PLEASE HELPP
If given the following situation; At a fair, each person can spin two wheels of chance. The first wheel has the numbers 1, 2, and 3. The second wheel has the letters A and B. Explain how you know if this game of chance is based on simple or compound probability.
Answers
Answer:
It is based on simple probability because there is only one possible answer each spin hope this helps :)
Step-by-step explanation:
the center for medicare services reported that there were 295,000 reported appeals for hospitalization and other medicare part a services. for this group, 40% of the first round appeals were successful. suppose ten first round appeals were just received. the results follow a binomial distribution. what is the probability exactly two of the appeals was successful? enter answer to four decimal places.
Answers
The probability exactly two of the appeals were successful is 0.9536
We are given that 40% of first-round appeals were successful (The Wall Street Journal, October 22, 2012), and suppose ten first-round appeals have just been received by a Medicare appeals office.
This situation can be represented through Binomial distribution as;
\(P(X=r)={}^{n}C_{r}(p)^r(1-p)^r\) where \(x=0,1,2,3.....\)
where, n = number of trials (samples) taken = 10
r = number of success
p = probability of success which in our question is % of first-round
appeals that were successful, i.e.; 40%
So, here X ~ Binom(n=10 , p=0.40
Probability that at least two of the appeals will be successful = P(X>=2)
P(X >= 2) = 1 - P(X = 0) - P(X = 1)
= 1 - \(^{10}C_{0}(0.40)^0(1-0.40)^{10-0}-^{10}C_{1}(0.40)^1(1-0.40)^{10-1}\)
= 1 - 0.00605 - 0.0403
= 0.9536
Hence, the probability exactly two of the appeals were successful is 0.9536
To learn more about Binomial distribution visits:
https://brainly.com/question/15074045
#SPJ4
32 lbs of apples cost $160. How much would 25 lbs cost? *
Answers
Answer:
$125
Step-by-step explanation:
If you divide 160 by 32 you will get 5 then you will multipy 5 by 25 to get $125
Answer
125$
Step-by-step explanation:
5x32=160
5x25=125
Each pound of apples is equivalent to 5$
draw a line segment of length 8 cm divide it in the ratio 5:3
plzzzz helpppp
Answers
Answer:
Draw the line segment AB = 7 cm.
Draw ray BX making an acute ∠ABX.
Along BX. mark off five points B1, B2, B3, B4 and B5. Join B2 to A.
Through B5 draw B5P || B2A, intersecting BA produced at P.
The point P so obtained is the required point which divides AB externally in the ratio 3:5.
5.78 admitting students to college. a selective college would like to have an entering class of 1000 students. because not all students who are offered admission accept, the college admits more than 1000 students. past experience shows that about 83% of the students admitted will accept. the college decides to admit 1200 students. assuming that students make their decisions independently, the number who accept has the b(1200, 0.83) distribution. if this number is less than 1000, the college will admit students from its waiting list. (a) what are the mean and the standard deviation of the number x of students who accept? (b) use the normal approximation to find the probability that at least 800 students accept. (c) the college does not want more than 1000 students. what is the probability that more than 1000 will accept? (d) if the college decides to decrease the number of admission offers to 1150, what is the probability that more than 1000 will accept?
Answers
(a) can be calculated using the binomial distribution formula, (b) find the probability that at least 800 students accept, (c) find the probability that more than 1000 students, (d) same approach as in part (c)
(a) The mean of the number of students who accept is calculated by multiplying the number of trials (1200) by the probability of success (0.83), resulting in 996 students. The standard deviation can be obtained by taking the square root of the product of the number of trials, the probability of success, and the probability of failure (1 - 0.83), resulting in approximately 9.91 students.
(b) To find the probability that at least 800 students accept, we can use the normal approximation to the binomial distribution. We calculate the z-score using the formula z = (x - np) / sqrt(np(1-p)), where x is the number of students (800), n is the number of trials (1200), p is the probability of success (0.83), np is the mean (996), and sqrt(np(1-p)) is the standard deviation (9.91). We then use the z-score to find the corresponding probability from the standard normal distribution table.
(c) To find the probability that more than 1000 students accept, we subtract the probability of 1000 or fewer students accepting from 1. We can use the same normal approximation approach as in part (b) but calculate the probability for 1000 students or fewer.
(d) By decreasing the number of admission offers to 1150, we can repeat the calculations from part (c) using the updated number of trials (1150) and the same values for p, mean, and standard deviation. This will give us the probability that more than 1000 students accept with the new admission offers.
Learn more about calculations here:
https://brainly.com/question/30151794
#SPJ11
Ralph wants to build a rectangular deck with a predefined area of 66 feet squared. One side of the deck will be 5 feet longer than the other. To find the side lengths, he first writes the equation (x)(x+5)=66 and later simplifies (x-6)(x+11)=0 it to , where x is the length of the shorter side. Which of these are the side lengths, in feet, of the rectangular deck? Select all that apply
Answers
Answer:
The shorter side is 6 ft and the longer side is 11 ftStep-by-step explanation:
The options are not given, but we could solve and arrive at an answer
say the shorter side is x
and the longer side is x+5
we know that the area of a rectangle is given as
x*(x+5)=66
open the bracket
x^2+5x=66
x^2+5x-66=0
Find two factors of -66 whose sum equals the coefficient of the middle term, which is 5 .
the factors are 11 and -6
splitting the middle term using the two factors 11 and -6
x2 +11x - 6x - 66=0
x(x+11)-6(x+11)=0
(x-6)=0
x=6
(x+11)=0
x=-11
The shorter side is 6 ft and the longer side is 11 ft
What is the value of \((8/3)+(-3)^2-(1/2)\)? (Write your answer as a fraction in reduced form).
Answers
Answer:
Exact Form 67/6
Mixed Number Form 11 1/6
Step-by-step explanation:
Removed Parenthesis 8/3+(-3)^2-1/2
Group like terms 8/3 - 1/2 + (-3)^2
Apply the exponent rule 8/3 - 1/2 + 3^2
Find the LCM (least common multiple) of 3 & 2; 6
Adjust Fraction based on LCM 8/3 = 8*2/3*2 = 16/6 1/2 = 1*3/2*3 = 3/6
16/6 - 3/6
since denominators are equal combine the fraction \(\frac{16-3}{6}\)
Subtract the numbers 3^2 + 13/6
3^2 = 9 = 9 +13/6
9*6/6 + 13/6
\(\frac{9*6 + 13}{6}\) = 67/6
Ethan played in two basketball games. He scored 4 fewer points in the second game than he scored in the first. He scored 12 points in the second game. How many points did he score in the first game?
Answers
9514 1404 393
Answer:
16 points
Step-by-step explanation:
You are given ...
second = first - 4
second = 12
Substituting the second equation into the first, we have ...
12 = first - 4
16 = first . . . . . . . . add 4 to both sides
Ethan scored 16 points in the first game.
The weather forecast calls for a total of 16 inches of snow over the next week. If it is estimated that 2.8 inches of snow will fall on Monday, 3.4 inches of snow will fall on Tuesday, 1.6 inches of snow will fall on Wednesday, 2.1 inches of snow will fall on Thursday, 1.7 inches of snow will fall on Friday, and 2.9 inches of snow will fall on Saturday. How much snow should fall on Sunday?
A.
3.2 inches
B.
3.6 inches
C.
1.5 inches
D.
0.5 inches
Answers
Which relationships describe angles 1 and 2?
Select each correct answer.
complementary angles
adjacent angles
supplementary angles
vertical angles

Answers
Answer: Supplementary angles
Step-by-step explanation:
Bye have a nice day.
Answer:
does this help answer your question? Answer: They are supplementary angles, because angle 1 + angle 2 = 180° , i.e. they form a line.
Step-by-step explanation:
I would suggest that you memorize these -
1. Complementary angles always =90°
For example, 30 degrees and 60 degrees are complementary angles.
2. Adjacent angles are two angles that have a common side and a common vertex (corner point) but do not overlap in any way. (share a side)
3. Supplementary angles are those that in sum give 180°.
4. Vertical angels ---- each of the pairs of opposite angles made by two intersecting lines.
So, what have you learned? You learned that complementary angles are two angles that add up to 90 degrees, supplementary angles are two angles that add up to 180 degrees, vertical angles are opposite angles at an intersection of two straight lines, and adjacent angles are two angles that are next to each other.
Two cars leave the same parking lot, with one heading north and the other heading east. After several minutes, the northbound car has traveled 8 miles, and the eastbound car has traveled 6 miles. Measured in a straight line, how far apart are the two cars?
Answers
When measured in straight line, the distance of the cars apart would be = 10 miles.
How to calculate the distance of the cars apart in straight line?To calculate the distance of the cars apart in a straight line, the Pythagorean formula should be used. That is;
C² = a²+b²
c² = 8²+6²
= 64+36
c² = 100
c = √100
= 10 miles
Learn more about triangle here:
https://brainly.com/question/28470545
#SPJ1
divide 600 in the ratio 2: 3: 4
Answers
Answer:
133.33, 200, 266.66
Step-by-step explanation:
GIven data
This is a ratio problem, and we will use the part to all method to get the solution
The given ratio is
= 2: 3: 4
the total ratio
=2+3+4
=9
Hence the first part is
2/9= x/600
cross multiply
9x= 1200
x= 1200/9
x= 133.33
The second part
3/9=x/600
1/3=x/600
3x=600
x=200
The third part
4/9=x/600
4/9=x/600
9x=600*4
9x=2400
x=2400/9
x=266.66
Therefore the figures are
133.33, 200, 266.66
Suppose that scores on a recent statistics exam were normally distributed, that students in the 80th percentile of scores earned 85 points, and that students in the 30th percentile of scores earned 65 points. What was the mean of all exam scores in the class?.
Answers
The mean of all exam scores in the class is found = 71
Normally distribution
A normal distribution is an arrangement of a data set in which most values cluster in the middle of the range and the rest taper off symmetrically toward either extreme.
While data points are referred to as x in a normal distribution, they are called z or z-scores in the z-distribution. A z-score is a standard score that tells you how many standard deviations away from the mean an individual value (x) lies: A positive z-score means that your x-value is greater than the mean.
The z-score is found by;
z = (x - μ)/σ
x = sample mean
μ = mean score
σ = standard deviation
Now, from this,
x = zσ + μ
For p = 80th percentile= 0.8, see z value from z score table.
z = 0.85
x = 85 points
85 = 0.85σ + μ .....eq 1
For p = 30% = 0.3, see the z value from the z score table.
z = -0.3802
x = 65
65 = -0.3802σ + μ .....eq 2
Solving eq 1 and 2.
σ = 16.25
Put in eq 1
μ = 71.19
μ = 71
Thus, the mean of all exam scores in the class is found = 71
To learn more about Normal Distribution visit:
brainly.com/question/13759327
#SPJ4