A mens basketball has a circumference of 29.5 inches. find the volume of the basketball to the nearest cubic inch. (hint must find the radius first. use the circumference formula
Answers
To find the volume of the basketball it is necessary to find the radius of the sphere, you do it by using the formula of the circumference and solving for r:
\(\begin{gathered} C=2\pi r \\ r=\frac{C}{2\pi} \end{gathered}\)Replace for the given value and find the radius:
\(\begin{gathered} r=\frac{29.5}{2\pi} \\ r=4.7 \end{gathered}\)Now, find the volume of the sphere using the following formula and replacing for the value of the radius:
\(\begin{gathered} V=\frac{4}{3}^{}\pi\cdot r^3 \\ V=\frac{4}{3}\pi(4.7)^3 \\ V=434.89\approx435 \end{gathered}\)The volume of the sphere is 435 in^3.
Related Questions
The graph shows a function of the form () = ab
.
Use the drop-down menus to complete the statements about the function, and then write an equation that represents this function.
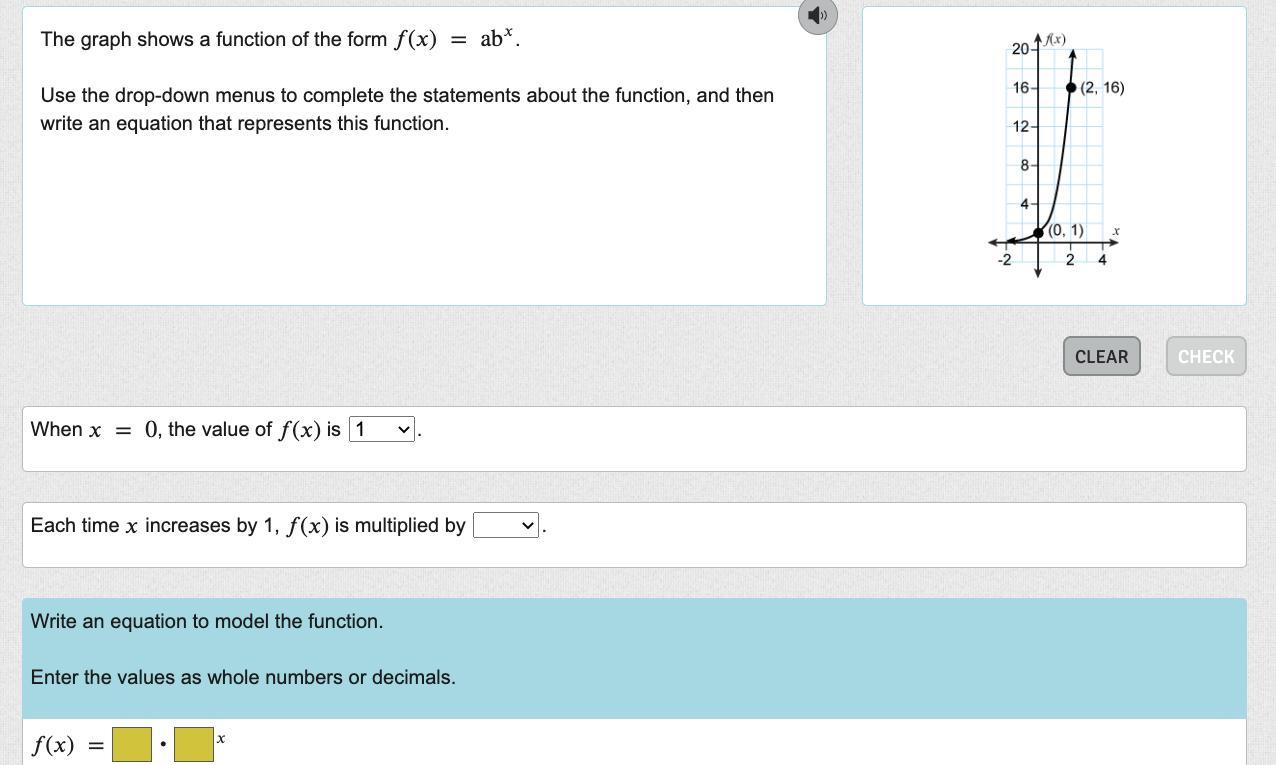
Answers
Answer:
When \(x=0\), the value of f(x) is 1.
Each time x increases by 1, f(x) is multiplied by 4.
Equation of function: \(f(x)=1\cdot 4^x\)
Step-by-step explanation:
The detailed explanation is attached below.

if fifteen families are coming to the picnic and they all split the cost evenly between them how much will each family contribute towards the cost of the shelter
Answers
Complete the equation using an area model 6 3/4 x 3 2/5=
Answers
Answer:
22.95
Step-by-step explanation:
Simplify the expression StartFraction a b Superscript 3 Baseline over a Superscript 4 Baseline b EndFraction plus left-parenthesis c Superscript 2 Baseline right-parenthesis Superscript 3 Baseline
Answers
The simplification of the expression ab³/a⁴b + (c²)³ is determined as b²/a³ + c⁶.
What is the simplification of the expression?The given expression is simplified as follows;
The given expression is written as;
ab³/a⁴b + (c²)³
To simplify the expression given above, we will divide the fraction with the common factor as follows;
From the numerator; ab³, we will factor out "ab"
From denominator; a⁴b, we will factor out "ab"
The resulting expression becomes;
ab³/a⁴b + (c²)³
= b²/a³ + c⁶
Note: for the power of c, we simplify by multiplying 2 and 3 = 6
Thus, the simplification of the expression ab³/a⁴b + (c²)³ is determined as b²/a³ + c⁶.
Learn more about simplification here: https://brainly.com/question/28008382
#SPJ1
-5 1/4 -(-7 1/2) simplify
really fast pleas
Answers
Jeff bought 7 pounds of chocolate
and spent $8.89. How much is one
pound of chocolate?
Answers
Answer:
1.27
Step-by-step explanation:
Answer:
$1.27
Step-by-step explanation:
Divide the total cost by the number of things you have to get the unit cost. Unit cost is the amount per item
$8.89/7 items = $1.27 per 1 pound of chocolate
Use the Quadratic Formula to solve the equation 4x^2+1=10x
Answers
Using the Quadratic Formula to solve the equation 4x² + 1 = 10x, we get x₁ = 0.104 and x₂ = 2.395.
What is Quadratic Formula?The term "quadratic equation" refers to an equation of the form ax2 + bx + c = 0, where a, b, and c are real numbers and a0 is an imaginary number. The quadratic equation's roots are the values of the unknown variable x that satisfy the given quadratic equation.
A + b + c, for instance, equals zero if is a root of the quadratic equation ax² + bx + c = 0. Additionally, the act of locating roots is referred to as solving a quadratic equation.
The quadratic formula is
\($ {\displaystyle \text x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}\)
We have given the quadratic equation 4x²+ 1 = 10x
= 4x² -10x + 1
Pouting the values in the formula we get
\({\displaystyle \text x={\frac {-(-10)\pm {\sqrt {(-10)^{2}-4(4)(1)}}}{2(4)}}}\)
On solving we get
\($ \text x_1 = \frac{5-\sqrt{21} }{4}\) and \($ \text x_2 = \frac{5+\sqrt{21} }{4}\)
Approximately,
x₁ = 0.104
x₂ = 2.395
Learn more about quadratic formula
https://brainly.com/question/2507588
#SPJ1
A chord is 15 cm long. It is 9 cm from the center of the circle. What is the radius of the circle?
Answers
Answer:
11.72cmStep-by-step explanation:
Given a chord of distance of 15cm, if it is 9cm from the center of a circle, this means that the 9cm length will be projecting from the centre of the circle perpendicular to the chord and passing through its centre.
Since the radius of a circle is a line that is drawn from the centre of a circle to ts circumference, the set up will form a right angles triangle within the circle with the hypotenuse as the radius and the other two sides as the opposite and adjacent respectively. Using the Pythagoras theorem to get the length of the radius (hypotenuse);
hyp² = opp² + adj²
Let the opposite be the 9cm length
Adjacent will be half of the chord length = 15/2 = 7.5cm
Substituting this values into the formula we will have;
hyp² = 9² + 7.5²
hyp² = 81+56.25
hyp² = 137.25
hyp² = √137.25
hyp = 11.72
Hence the radius of the circle is approximately 11.72 cm long
s is inversely proportional to t . When s = 0.9 , t = 2 Work out t when s = 30
Answers
Hope you will understand

Answer:
Step-by-step explanation:
we can assume that s=k/t,k is unknown constants,0.9=k/2 >> k=1.8,so
30=1.8/t >> t=0,06
Is (1,8), (2,12), (3,16) (4,20) a function?
Answers
2
Let g(x) = x + 4x-7.
What is g(x) in graphing form?
(x + 2) - 7 = 4
O g(x) = (x + 2)²-7
Onone of the answer choices
x² + 4x-7=0
O g(x) = (x + 2)² - 11

Answers
The graphing form of the function g(x) is: C) none of the answer choices.
The function g(x) = \(x^2 + 4x - 7\)is already in the standard form of a quadratic equation. In graphing form, a quadratic equation can be represented as y =\(ax^2 + bx + c,\) where a, b, and c are constants.
Comparing the given function g(x) =\(x^2 + 4x - 7\)with the standard form, we can identify the coefficients:
a = 1 (coefficient of x^2)
b = 4 (coefficient of x)
c = -7 (constant term)
Therefore, the graphing form of the function g(x) is:
C) none of the answer choices
None of the given answer choices (A, B, D, or E) accurately represents the graphing form of the function g(x) =\(x^2 + 4x - 7\). The function is already in the correct form, and there is no equivalent transformation provided in the answer choices. The given options either represent different equations or incorrect transformations of the original function.
In graphing form, the equation y = \(x^2 + 4x - 7\) represents a parabolic curve. The coefficient a determines the concavity of the curve, where a positive value (in this case, 1) indicates an upward-opening parabola.
The coefficients b and c affect the position of the vertex and the intercepts of the curve. To graph the function, one can plot points or use techniques such as completing the square or the quadratic formula to find the vertex and intercepts. Option C
For more such questions on graphing visit:
https://brainly.com/question/19040584
#SPJ8
Parametric Functions

Answers
Answer:
Step-by-step explanation:
it think it 23 becasue u add
1 divide it by 2
compute the volume of the solid formed by revolving the region bounded by x=y^2 and x=4 about the line y=3
Answers
The volume of the solid formed by revolving the region bounded by x = \(y^2\) and x = 4 about the line y = 3.
To find the volume of the solid formed by revolving the region bounded by x = \(y^2\) and x = 4 about the line y = 3, we can use the method of cylindrical shells.
First, let's determine the limits of integration. From the given equations, we can see that the region of interest lies between y = -2 and y = 2 because \(y^2\) = 4 when y = ±2.
Next, we express the equation x = \(y^2\) in terms of y:
x = \(y^2\)
To set up the integral for the volume, we need to consider the radius and height of each cylindrical shell. The radius is the distance between the line of revolution y = 3 and the curve x =\(y^2\), which is given by:
r = 4 - \(y^2\)
The height of each shell is the infinitesimal change in y, dy.
Now we can set up the integral:
V = ∫[from y = -2 to y = 2] 2πrh dy
V = ∫[from y = -2 to y = 2] 2π(4 - \(y^2\))(3 - y) dy
Therefore, evaluating this integral will give us the volume of the solid formed by revolving the region bounded by x =\(y^2\) and x = 4 about the line y = 3.
For more such answers on volume
https://brainly.com/question/463363
#SPJ11
Find X
I’m kinda lazy rn
Thanks lol

Answers
In a recent year there were the following numbers (in thousands) of licensed drivers in the United States.MaleFemaleAge 19 and under4746 4517Age 201625 1553Age 211679 1627Source: World Almanac.Choose one driver at random. Find the following probability of selecting the driver. Round your answers to three decimal places.P (male and age 20) =
Answers
There are 1625 males of 20 years out of a total of:
\(4746+4517+1625+1553+1679+1627=15747\)To find the probability of choose a male and at age 20, we divide the possibilities by the total:
\(\frac{1625}{15747}\approx0.103194\)the probability of choose a male and at age 20 is 0.103
Ali, Basti and Cian stand at three points A, B and C respectively. Suppose that the measure of angle ABC is 50 degrees , the measure of angle BAC is 60 degrees and Ali is exactly 150 ft away from Basti. Find the distance between Basti and Cian.

Answers
The distance between Basti and Cian is approximately 138.2 ft. Option D
To find the distance between Basti and Cian, we can use the Law of Sines, which relates the lengths of sides to the sines of their opposite angles in a triangle.
Let's label the points: A, B, and C. Ali is at point A, Basti is at point B, and Cian is at point C.
Given:
Angle ABC = 50 degrees (angle opposite side AC)
Angle BAC = 60 degrees (angle opposite side BC)
Ali is 150 ft away from Basti (side AB)
We want to find the distance between Basti and Cian, which is side BC.
Using the Law of Sines, we have:
BC/sin(50) = AB/sin(60)
Substituting the known values:
BC/sin(50) = 150/sin(60)
To find BC, we can rearrange the equation:
BC = (150/sin(60)) * sin(50)
Using a calculator to evaluate the expression:
BC ≈ 138.2 ft
Option D is correct.
For more such questions on distance visit:
https://brainly.com/question/30395212
#SPJ8
A right triangle has one leg 3 meters long and a hypotenuse 5 meters long. What is the length of the other leg? A. 4 m B. 5 m C. 15 m D. 25 m
Answers
Answer:
A
Step-by-step explanation:
Using the Pythagorean Theorem, you can find that the length of the final leg is:
\(\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16}=4\)
Therefore, the answer is A. Hope this helps!
Need help on this! (Many points!)

Answers
Answer:
\(\frac{-8}{9}\)
Step-by-step explanation:
Substitute in 7 for x
\(\frac{7^{2}-5(7) -6 }{7^{2}-6(7) - 16 }\)
\(\frac{49-35-6}{49-42-16}\)
\(\frac{-8}{9}\)
if you take away 25 from a number you will be left with two and halftimes 30. what is the number?
Answers
If you take away 25 from (100) you get 75.
70 also equals 2.5*30
What is the distance between the points (-2,1) and (5,-4)
Answers
Considering the definition of distance between two points, the distance between the points (-2,1) and (5,-4) is √74= 8.6023.
Distance between two pointsThe distance between two points is equal to the length of the segment that joins them. Therefore, to determine the distance between two different points, you must calculate the squares of the differences between their coordinates and then find the root of the sum of said squares.
In other words, the distance between two points in space is the magnitude of the vector formed by said points.
So, given the coordinates of two distinct points (x1, y1) and (x2, y2), the distance between two points is the square root of the sum of the squares of the difference of the coordinates of the points:
distance= \(\sqrt{(x2-x1)^{2} +(y2-y1)^{2} }\)
Distance between the points (-2,1) and (5,-4)In this case, you know:
(x1, y1): (-2,1)(x2, y2): (5,-4)Replacing in the definition of distance:
distance= \(\sqrt{(5-(-2))^{2} +(-4-1)^{2} }\)
distance= \(\sqrt{(5+2)^{2} +(-5)^{2} }\)
distance= \(\sqrt{7^{2} +(-5)^{2} }\)
distance= \(\sqrt{49+25 }\)
distance= √74= 8.6023
Finally, the distance between the points (-2,1) and (5,-4) is √74= 8.6023.
Learn more about distance between two points:
https://brainly.com/question/23848540
https://brainly.com/question/7243416
https://brainly.com/question/15973889
#SPJ1
Which ordered pair solves this linear system?
Y= -x
Y= 2x
Answers
The ordered pair that solves the system of equation is (0, 0).
To solve this system, we can substitute the first equation into the second equation to eliminate y:
x = 2x
Solving for x, we get x = 0.
Substituting x = 0 into the first equation, we get y = 0.
Therefore, the ordered pair that solves the system is (0, 0).
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
=5−82 find slope value
Answers
A number n minus the sum of the number and eight
Answers
The algebraic expression for the sentence in this problem is given as follows:
n - (x + 8).
How to obtain the algebraic expression for the sentence?The sentence in this problem is given as follows:
"A number n minus the sum of the number and eight".
The sum of an unknown number x and eight is given as follows:
x + 8.
The subtraction of the number n by the expression is given as follows:
n - (x + 8).
More can be learned about algebraic expressions at https://brainly.com/question/4344214
#SPJ1
A restaurant has 60 menu items. Of these menu items, main dishes outnumber
appetizers by a ratio of 4:1. How many more appetizers would the restaurant have
to add to the menu to bring the ratio to 2:1?
Answers
Answer:
15 more appetizers
Step-by-step explanation:
A restaurant has 60 menu items. Of these menu items, main dishes outnumber appetizers by a ratio of 4:1. How many more appetizers would the restaurant have to add to the menu to bring the ratio to 2:1?
at a ratio of 4e:1a and having 60e: there are (60/4=15) 15 appetizers
at a ratio of 2e:1a and having 60e: there are (60/2=30) 30 appetizers
Because they already have 15 appetizers, they will need:
30 appetizers - 15 appetizers = 15 more appetizers
if a coin is flipped three times the probability of getting heads all three times
Answers
The probability of getting head three successive times can be written as;
\(Pr(\text{ three heads)}\)This is also equal to;
\(undefined\)Suppose you want to simulate something with a 16% (4 in 25) chance of success. The most efficient way to simulate that with whole numbers would be to generate the numbers from 1 to______ , and arbitrarily choose number(s)___________ to represent a "success."
Answers
Answer:
25
6, 12, 18, 24 (Any four numbers from 1 to 25 would be correct)
Step-by-step explanation:
The most effective way to this with whole numbers is to find an irreducible fraction that represents 16%. Coincidentally, we were already given that 16% represents a 4 in 25 chance, which is an irreducible fraction.
Therefore, the most efficient way to do it is to generate numbers from 1 to 25, and then arbitrarily choose any four numbers (i.e. 6, 12, 18, 24) within that range to represent a success.
What the surface area

Answers
Step-by-step explanation:
the surface area is the sum of all areas of the individual outside faces/sides.
so, what do we see here, what outside sides do we have here ?
of course, we have to assume that this is a regular object (left and right sides are the same).
2 right-angled triangles (left and right).
1 rectangle in the back.
1 rectangle at the bottom.
1 times rectangle in the front.
the area of a right-angled triangle is
leg1 × leg2 / 2
in our case that is
6 × 2.5 /2 = 3 × 2.5 = 7.5 mm²
we have 2 of these triangles :
2×7.5 = 15 mm²
the area of the rectangle in the back is
8 × 6 = 48 mm²
the area of the rectangle at the bottom is
8 × 2.5 = 20 mm²
the area of the rectangle in the front is
8 × 6.5 = 52 mm²
the surface of the object is the sum of all that :
15 + 48 + 20 + 52 = 135 mm²
Find the output, y, when the input, x, is -9.
y =

Answers
Answer:
when x=-9, y=1
Step-by-step explanation:
the graph shows when the x is at -9, the y is at 1

NEED HELP THANKS IN ADVANCE.

Answers
Answer:
b
Step-by-step explanation:
Answer:
3x^5 - 5x^3+2x^2-10x +4 = 4x^4 + 6x^3-11can be solved by using this system of equations.
Find an equation of the line that satisfies the given conditions.
Through (−1, −2); perpendicular to the line 2x + 7y + 6 = 0
Answers
if two lines are perpendicular it means their slopes are negative reciprocals of one another. So, if the slope of the given line is 2, the slope of the line we are trying to find is -1/2.
To find “b” (the y-intercept) we have to plug in the given point into y=mx+b with the slope we just found;
y = mx+b
-2 = (-1/2)(-1) + b
-2 = 1/2 + b
-2 - 1/2 = b
-5/2 = b
the EOL is y = -1/2x - 5/2