A large population is bi-modal (like you'd get if you included the heights of
both men and women in the same distribution). samples of size 40 are drawn
and a sampling distribution of the mean values of these samples is
constructed. what's the most likely shape of the sampling distribution of the
sample mean?
Answers
Answer:
Approximately normal, as predicted by the Central Limit Theorem
Step-by-step explanation:

Related Questions
A hat is 40% off the discount price of a hat is $50.40 what is the regular price
Answers
Answer:
The correct answer would be $126.00
Step-by-step explanation:
If you see how many times 40% goes into 100%, it would be 2.5 times. Then you multiply the 40% of the overall price ($50.40) times 2.5 and that gives you $126.
Hope this helps!!
What is the sum of all the angles that are labeled?
Image of three angles around a single vertex. One angle is fifty five degrees, one is sixty four degrees, and one is one hundred seventy five degrees.
Answers
The sum of all the angles that are labeled in the given vertex is 294°
In a single vertex, the three angles around the vertex are given as 55°, 64°, and 175°
We have to find the sum of all the angles that are labeled in the given single vertex.
What is a vertex?A vertex is a point two or more lines meets.
It is the corner of a geometrical shape.
Example:
A square has 4 corners so it has 4 vertexes.
A cube has 8 corners so it has 8 vertexes.
We will add all the different angles in the single vertex as shown in the figure below.
Let,
Angle A = 55°
Angle B = 64°
Angle C = 175°
The sum of all the angles that are labeled is:
= Angle A + Angle B + Angle C
= 55° + 64° + 175°
= 294°
The sum of all the angles that are labeled in the given vertex is 294°
Learn more about the vertex here:
https://brainly.com/question/12563262
#SPJ1

Which of the following statements is true regarding the influence of a small alpha level in the context of hypothesis testing? O a. A small alpha level reduces the effect size. O b. A small alpha level increases statistical power. c. A small alpha level reduces the likelihood of a Type I error. O d. A small alpha level increases the likelihood of detecting statistical significance
Answers
The influence of a small alpha level in the context of hypothesis testing is:
c. A small alpha level reduces the likelihood of a Type I error.
What is null hypothesis?A hypothesis known as the null hypothesis states that sample observations are the result of chance.
The correct statement regarding the influence of a small alpha level in the context of hypothesis testing is:
c. A small alpha level reduces the likelihood of a Type I error.
A small alpha level (typically denoted as α) is the significance level used in hypothesis testing to determine the threshold for rejecting the null hypothesis. By setting a small alpha level, such as 0.01 or 0.05, we are reducing the probability of making a Type I error, which is the incorrect rejection of a true null hypothesis.
In other words, a small alpha level provides a stricter criterion for rejecting the null hypothesis, making it less likely to reject the null hypothesis when it is true. This reduces the likelihood of claiming a significant result when there is no true effect or relationship in the population.
Learn more about null hypothesis on:
https://brainly.com/question/28042334
#SPJ4
Find the slope of the line without graphing using the 2 points below.
(-2, -1) & (-8 , 11)
m = _______
Answers
Answer:
m = -2
Step-by-step explanation:
1. use the slope formula --> (y2-y1)/(x2-x1)
2. (11 -(-1))/(-8 -(-2))
3. 12/-6
4. m = -2
Answer:
The slope is -2
Step-by-step explanation:
We can use the slope formula
m = ( y2-y1)/(x2-x1)
= ( 11- -1)/( -8 - -2)
( 11+1)/( -8+2)
12/-6
-2
Can someone please help me?
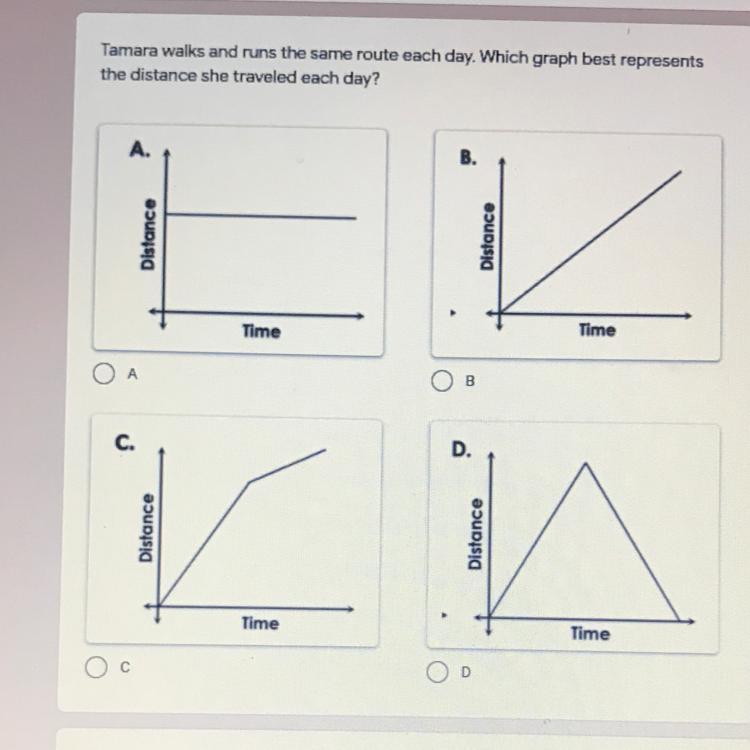
Answers
Answer:5
Step-by-step explanation: the like moves at and angle bc u started going faster due to running
Answer:
B
Step-by-step explanation:)
Look at the graph it shows her walking the rest don't make sense
What is the equation of the line that passes through the point (-5,-2) and has a slope of 3/5?
Answers
Answer:
y = 3/5x + 1
Step-by-step explanation:
Formula:
y - y1 = m(x - x1)
Plug in:
y - (-2) = 3/5(x - (-5))
Two negatives make a positive:
y + 2 = 3/5(x +5)
Distribute 3/5 to (x + 5):
y + 2 = 3/5x + 3
Get y by itself by - 2:
y = 3/5x + 1
Hope this helps you :)
Please help...Will give brainiest

Answers
Answer:
19.45
Step-by-step explanation:
The median is the middle number. Put the data in order from smallest to largest
16.3, 17.8,17.8 ,18.0, 18.7,19.3, 19.6,20.1,20.5, 21.9, 25.2 ,25.4
There are 12 pieces of data,
16.3, 17.8,17.8 ,18.0, 18.7,19.3, 19.6,20.1,20.5, 21.9, 25.2 ,25.4
The median lies between the 6th and 7th piece
Add the 6th and 7th together and divide by 2
(19.3+19.6)/2 =19.45
Answer:
\(\large \boxed{\mathrm{19.45}}\)
Step-by-step explanation:
Median of a data set is the middle value.
The data is to be arranged from smallest to largest.
16.3, 17.8, 17.8, 18.0, 18.7, 19.3, 19.6, 20.1, 20.5, 21.9, 25.2, 25.4
Find the middle value.
16.3, 17.8, 17.8, 18.0, 18.7, 19.3, 19.6, 20.1, 20.5, 21.9, 25.2, 25.4
Average the two middle numbers.
(19.3+19.6)/2 = 19.45
The median of the data set is 19.45.
Given that is the midpoint of AB and E is the midpoint of AC, AD =32cm, AE=19cm, and DE=39cm, determine the perimeter of DBCE

Answers
Answer:
since triangle AED similar to ACB
CE=19cm mid point bisect it
BD=32Cm mid point bisect it
Step-by-step explanation:
BC=2DE=2×39=78Cm
perimeter=sum of all side=ce+de+bd+bc=19+39+32+78=168cmtherefore perimeter of DBCE=168Cmfind the surface area for a sphere with a radius of 10 feet. round to the nearest whole number. a. 1,256 ft2b. 4,189 ft2c. 1,089 ft2d. 1,568 ft2
Answers
The surface area of a sphere with a radius of 10 feet is approximately 1,256 ft².
The surface area of a sphere refers to the total area that covers the surface of the sphere. It is the sum of all the areas of the small flat faces that make up the sphere.
To find the surface area of a sphere with a radius of 10 feet, we need to use the formula:
Surface Area = 4πr²
Where r is the radius of the sphere.
Plugging in the value of r=10 into the formula, we get:
Surface Area = 4π(10) = 400π
Since π is an irrational number, we cannot calculate its exact value. However, we can approximate it to 3.14. Therefore,
=> Surface Area = 400 * 3.14 = 1256
Rounding to the nearest whole number, we get the surface area of the sphere with a radius of 10 feet as 1,256 ft², which is option (a).
To know more about surface area here.
https://brainly.com/question/28855092
#SPJ4
3. Find the average value of the function f(x) = e-4ª on the interval [0, 2].
Answers
The average value of f(x) on [0, 2] is 0.2497.
The formula for the average value of a function f(x) on the interval [a, b] is given by: Average value of f(x) on [a, b] = 1/(b-a) ∫a^bf(x) dx Given, f(x) = e^(-4x) and the interval [0, 2]So, we have to find the average value of f(x) on [0, 2]Using the formula we have, Average value of f(x) on [0, 2] = 1/(2 - 0) ∫0^2 e^(-4x) dx = 1/2 ∫0^2 e^(-4x) dx Let's evaluate the integral now. ∫e^(-4x) dx = -1/4 e^(-4x) + C [ Integrating e^(-4x) with respect to x]Putting the limits in the above equation,-1/4 e^(-4x) [ from 0 to 2] = -1/4 [ e^(-8) - e^0 ] = -1/4 [ 0.0003 - 1 ] = 0.2497 Hence, the average value of f(x) on [0, 2] is 0.2497.
In this problem, we have to find the average value of f(x) = e^(-4x) on the interval [0, 2].Using the formula for the average value of a function f(x) on the interval [a, b], we have the average value of f(x) on [0, 2] = 1/(2 - 0) ∫0^2 e^(-4x) dx = 1/2 ∫0^2 e^(-4x) dx Evaluating the integral, we get ∫e^(-4x) dx = -1/4 e^(-4x) + C [ Integrating e^(-4x) with respect to x]. Putting the limits in the above equation, we get -1/4 e^(-4x) [ from 0 to 2] = -1/4 [ e^(-8) - e^0 ] = -1/4 [ 0.0003 - 1 ] = 0.2497.
To know more about value visit:-
https://brainly.com/question/30145972
#SPJ11
Find the product of 1,230,000 and (0.4 · 10-8). In your final answer, include all of your calculations.
Answers
Answer:
-4,920,000
Step-by-step explanation:
Product means multiplication:
1,230,000(0.4 x 10 - 8)
1,230,000(4 - 8)
1,230,000(-4)
-4,920,000
If you take the opposite of the product of 8 and -2, will the answer be less than -5, between -5 and 5 and 10, or greater than 10?
Answers
Answer: Greater than 10.
8x-2=-16 the inverse (opposite) of -16 is 16. 16 is greater than 10.
An expert witness for a paternity lawsuit testifies that the length of a pregnancy is normally distributed with a mean of 280 days and a standard deviation of 13 days. An alleged father was out of the country from 240 to 306 days before the birth of the child, so the pregnancy would have been less than 240 days or more than 306 days long if he was the father. The birth was uncomplicated, and the child needed no medical intervention. What is the probability that he was NOT the father? What is the probability that he could be the father? Calculate the z-scores first, and then use those to calculate the probability.
Answers
The probability that the alleged father was not the father is: 0.024, or 2.4% and The probability that the alleged father could be the father is: 0.953, or 95.3%.
To calculate the probability that the alleged father was not the father, we first need to calculate the z-score for a pregnancy length of 240 days and for a pregnancy length of 306 days. The z-score formula is:
z = (x - mu) / sigmawhere x is the pregnancy length, mu is the mean pregnancy length, and sigma is the standard deviation of pregnancy length.
For a pregnancy length of 240 days, the z-score is:
z = (240 - 280) / 13 = -3.08For a pregnancy length of 306 days, the z-score is:
z = (306 - 280) / 13 = 2.00To calculate the probability that the alleged father was not the father, we need to find the area under the normal distribution curve to the left of the z-score for a pregnancy length of 240 days and to the right of the z-score for a pregnancy length of 306 days, and then add these probabilities together. Using a standard normal distribution table or calculator, we find that the probability to the left of z = -3.08 is approximately 0.001, and the probability to the right of z = 2.00 is approximately 0.023. Therefore, the probability that the alleged father was not the father is:
0.001 + 0.023 = 0.024, or 2.4%To calculate the probability that the alleged father could be the father, we need to find the area under the normal distribution curve between the z-scores for a pregnancy length of 240 days and a pregnancy length of 306 days. Using a standard normal distribution table or calculator, we find that the probability between z = -3.08 and z = 2.00 is approximately 0.953. Therefore, the probability that the alleged father could be the father is:
0.953, or 95.3%Learn more about probability
https://brainly.com/question/24756209
#SPJ4
Find the area of the following polygon if AB= 12 cm, AC = 2.4 cm, CE = 6 cm, AD 4.8 cm, CF = GE = 3.6 cm, DH = 2.4 cm. =
Answers
Answer:
50.40 cm2
Step-by-step explanation:
Area of the polygon AFGBH = Area of ∆ACF + Area of rectangle FCEG + Area of ∆GEB + Area of ∆ABH
= 3.6 cm2 + 4.32 cm2 + 21.6 cm2 + 6.48 cm2 + 14.4 cm2
= 50.40 cm2
Hence, the required area = 50.40 cm2.
How are the quotients shown
related?− 30 ÷ 6 and 30 ÷ (− 6)
Answers
Answer:
They both equal -5.
Find the missing coefficient in the equation of the line shown. Ax-4y=-1 (6,1). Write the completed equation.
Answers
a6 -4 = -1 (+4)
a6 = 3 / 6
a = 1/2
The required equation is (1/2)x - 4y = -1 and the value of the missing coefficient is A = 1/2.
What is an equation?The equation is defined as mathematical statements that have a minimum of two terms containing variables or numbers that are equal.
We have been given an equation as
Ax - 4y = -1 ....(i)
Point (6,1) which is given in the question,
Substitute the value of x = 6 and y = 1 in the above equation,
A(6) - 4(1) = -1
A6 -4 = -1 (+4)
A6 = 3 / 6
Reduce the fraction in the above equation,
A = 1/2
Substitute the value of A = 1/2 in the equation (i),
So (1/2)x - 4y = -1
Therefore, the required equation is (1/2)x - 4y = -1 and the value of the missing coefficient is A = 1/2.
Learn more about the equations here:
brainly.com/question/10413253
#SPJ2
Please help solve this by tomorrow

Answers
Answer:
4. A
5.C
6.B
7.d
8.d
9.d
10.c
11.A
12.b
13.F
14.g
15.g
16.g
17.A
Step-by-step explanation:
sana po makatulong pa brainlist nadin po :)
Use the Venn diagram to calculate probabilities.
Circles A, B, and C overlap. Circle A contains 12, circle B contains 11, and circle C contains 4. The overlap of A and B contains 5, the overlap of B and C contains 3, and the overlap of C and A contains 6. The overlap of the 3 circles contains 8.
Which probabilities are correct? Select two options.
P(A|C) = Two-thirds
P(C|B) = StartFraction 8 Over 27 EndFraction
P(A) = StartFraction 31 Over 59 EndFraction
P(C) = Three-sevenths
P(B|A) = StartFraction 13 Over 27 EndFraction
Answers
Answer:
The first one
The fourth one
Step-by-step explanation:
Draw a venn diagram (see picture)
A|C= (A∩C)/C
(6+8)/(6+8+3+4)= 2/3
C|B= (C∩B)/B
(8+3)/(11+5+8+3)= 11/27
A=(12+5+8+6)/(11+5+8+3+4+6+12) = 31/49
C= (4+6+8+3)/(12+5+11+6+8+3+4)= 3/7
P(B|A)= (B∩A)/A
(5+8)/(12+5+6+8) = 13/31

Answer:
A and D
Step-by-step explanation:
edge 2021
Find the area. The figure is not drawn to scale.

Answers
8 x 3.3 x 1/2 = 13.2.
Dadas as sequências identifique quais são PA e a sua razão (r): Lembre-se: para ser uma PA a diferença entre dois termos consecutivos são sempre os mesmos e é chamada de razão (r). A) (1, 1, 1, 1, ...) B) (-1, 0, 1, 2,...) C) (12, 48, 84, 120,...) D) (101, 202, 303, 404,...)
Answers
Answer:
A) 0
B) 1
C) 36
D) 101
Question:
Given the strings, identify which PA are and their reason (r): Remember: to be a PA the difference between two consecutive terms is always the same and is called the (r) ratio. A) (1, 1, 1, 1, ...) B) (-1, 0, 1, 2, ...) C) (12, 48, 84, 120, ...) D) (101 , 202, 303, 404, ...)
Step-by-step explanation:
PA is said to be the difference between two consecutive terms. The PA is always the same for these terms. It is also called the (r) ratio.
A) (1, 1, 1, 1, ...)
PA = 2nd term - 1st term = 3rd term - 2nd term
Using the 1st and second term
1st term = 1
2nd term = 1
PA = 1-1
PA = 0
B) (-1, 0, 1, 2, ...)
PA = 2nd term - 1st term = 3rd term - 2nd term
Using the 1st and second term
1st term = -1
2nd term = 0
PA = 0- (-1) = 0+1
PA = 1
C) (12, 48, 84, 120, ...)
PA = 2nd term - 1st term = 3rd term - 2nd term
Using the 1st and second term
1st term = 12
2nd term = 48
PA = 48 - 12
PA = 36
D) (101 , 202, 303, 404, ...)
PA = 2nd term - 1st term = 3rd term - 2nd term
Using the 1st and second term
1st term = 101
2nd term = 202
PA = 202 -101
PA = 101
Use the method given in the proof of the Chinese Remainder Theorem (Theorem 11.8) to solve the linear modular system {x = 5 (mod 9), x = 1 (mod 11)}. Theorem 11.8. (Chinese Remainder Theorem) Let m, n E N with gcd(m, n) = 1, and let a, b E Z. Then the system of linear modular equations {x = a (mod m), x = b (mod n)} has exactly one solution in [0, mn).
Answers
The linear modular system {x = 5 (mod 9), x = 1 (mod 11)} can be solved using the Chinese Remainder Theorem. The solution is x ≡ 46 (mod 99).
According to the Chinese Remainder Theorem, we need to find a number x that satisfies both congruences: x ≡ 5 (mod 9) and x ≡ 1 (mod 11).
First, we observe that gcd(9, 11) = 1, indicating that the moduli are relatively prime. To find the solution, we can use the method given in the proof of the Chinese Remainder Theorem.
Let's solve the congruence x ≡ 5 (mod 9) first. We can express 5 as a multiple of 9 plus a remainder: 5 = 0 * 9 + 5. This implies that x = 9k + 5 for some integer k.
Substituting x into the second congruence, we get 9k + 5 ≡ 1 (mod 11). Simplifying this equation, we have 9k ≡ 8 (mod 11). To find the value of k, we can use the extended Euclidean algorithm or by inspection determine that k ≡ 7 (mod 11).
Now, substituting k = 7 into x = 9k + 5, we find x = 9 * 7 + 5 = 68.
To find the general solution, we need to add the modulus of the two congruences, which gives us 9 * 11 = 99. Therefore, the final solution is x ≡ 68 (mod 99).
Learn more about Chinese Remainder Theorem here:
https://brainly.com/question/30806123
#SPJ11
Write the radian measure of each angle with the given degree measure explain your reasoning
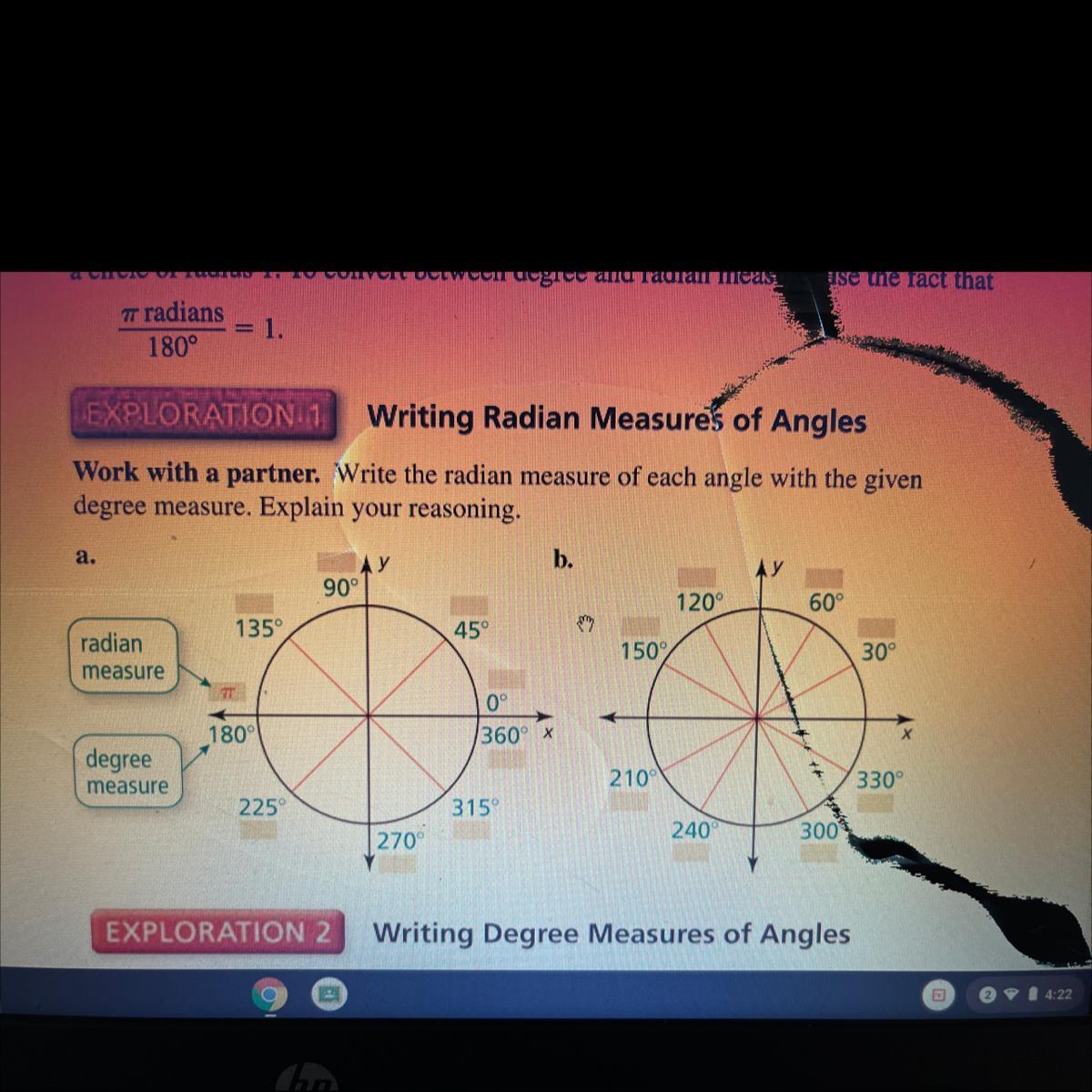
Answers
Answer:
90 = π/2
45 = π/4
0 and 360 = 0 and 2π
135 = 3π/4
180 = π
225 = 5π/4
270 = 2π/3
315 = 7π/4
315 =
Step-by-step explanation:
Read the introduction below and determine which element is missing.
What's black, white, and famous for sitting atop firetrucks for centuries? Since the 1800s, this spotted breed has been famous for its courage and bravery. Firefighters began using this persistent pooch, the dalmatian, because of its ability to get along with horses that pulled fire carriages before trucks existed.
General information
Hook
Thesis
Topic
Answers
Based on the introduction given, the element that is missing from excerpt is the Topic.
What element is missing?The element that is missing in this introduction to the use of Dalmatians by Firefighters is a topic. The topic is the element that would give clues about what the text is about.
The hook is the statement that grabs the reader which in this case is, "What's black, white, and famous for sitting atop firetrucks for centuries?" and there was general information provided on the Dalmatian use by firefighters.
Find out more on elements of writing at https://brainly.com/question/2761431
#SPJ1
Answer: Thesis (C)
Step-by-step explanation: Due to the other answer being wrong, topic is out, it has general info, thats out, it has a hook, thats out, meaning the answer must be "Thesis".
What is the product of 2 over 3y and y?
12 over 3y
2 over 3
2 over 3y
22 over 3y
Answers
The product of 2/3y and y is \(2/3y^2.\)
The product of 2/3y and y can be found by multiplying the numerators and denominators separately.
To multiply the numerators, we multiply 2 and 1 (since y can be written as y/1).
This gives us 2.
To multiply the denominators, we multiply 3y and 1.
This gives us 3y.
Therefore, the product of 2/3y and y is \(2/3y * y =\) \(2/3y^2.\)
In general, when multiplying fractions, we multiply the numerators and the denominators separately.
So, if we have a fraction a/b and another fraction c/d, their product would be ac/bd.
However, in this specific case, the expression can be simplified further.
Since we have y in both the numerator and denominator, they cancel out, leaving us with \(2/3y^2.\)
To summarize, the product of 2/3y and y is \(2/3y^2.\)
For more questions on product
https://brainly.com/question/28782029
#SPJ8
Match each equation to its factorized version and solution. 24x – 6x2 = 0 2x(x 3) = 0 solution: x = 0, x = -3 14x – 7x2 = 0 6x(4 – x) = 0 solution: x = 0, x = 4 2x2 6x = 0 x(4 – x) = 0 solution: x = 0, x = 4 4x – x2 = 0 7x(2 – x) = 0 solution: x = 0, x = 2
Answers
So, The correct match of these quadratic equations are
Equation A has a solution x = 3 and x = 0.
Equation B has a solution x = 2 and x = 4.
Equation C has a solution x = -3 and x = 0.
Equation D has a solution x = 4 and x = 0.
According to the equation
we have given that the some equation with there values of the x and we have to find and match the correct statement with the given values of x.
So, For this purpose, we know that the
The given quadratic equations are:
A. 24x – 6x^2 = 0 and 2x(3x) = 0 with solution x = 0, x = -3
B. 14x – 7x^2 = 0 and 6x(4 – x) = 0 with solution x = 0, x = 4
C. 2x^2+ 6x = 0 and x(4 – x) = 0 with solution x = 0, x = 4
D. 4x – x^2 = 0 and 7x(2 – x) = 0 with solution x = 0, x = 2
And now we solve it
So,
Take A.
24x – 6x^2 = 0 and 2x(3x) = 0
6x(3 -x) = 0 And 6x^2 = 0
here x = 3 and x = 0.
And
Take B.
14x – 7x^2 = 0 and 6x(4 – x) = 0
7x(2 -x) = 0 And 6x(4 – x)= 0
here x = 2 and x = 4.
And
Take C.
2x^2+ 6x = 0 and x(4 – x) = 0
2x(x +3) = 0 And x(4 – x)= 0
here x = -3 and x = 0.
And
Take D.
4x – x^2 = 0 and 7x(2 – x) = 0
x(4 -x) = 0 And 7x(2 – x)= 0
here x = 4 and x = 0.
So, The correct match of these quadratic equations are
Equation A has a solution x = 3 and x = 0.
Equation B has a solution x = 2 and x = 4.
Equation C has a solution x = -3 and x = 0.
Equation D has a solution x = 4 and x = 0.
Learn more about quadratic equations here
https://brainly.com/question/1214333
#SPJ4
Plz help will mark brainliest

Answers
Answer:
Hmmmm...I believe the answer is letter D.
Find the measures of the numbered angles in the isosceles trapezoid shown below.

Answers
First, notice that since we have an isosceles trapezoid, the base angles will be equal, then:
\(\measuredangle3=60\degree\)next, we have that the angles adjacent to opposite bases are supplementary, then we can write the following equation:
\(\measuredangle2+\measuredangle3=180\)using the fact that the measure of angle 3 is 60 degrees, we can find the measure of angle 2:
\(\begin{gathered} \measuredangle2+60=180 \\ \Rightarrow\measuredangle2=180-60=120 \\ \measuredangle2=120 \end{gathered}\)then, since angles 1 and 2 are also base angles, they are equal. Therefore, the measure of the anlges is:
\(\begin{gathered} \measuredangle1=120 \\ \measuredangle2=120 \\ \measuredangle3=60 \end{gathered}\)PLEASE I NEED THIS NOW 50 POINTS
Write your answer as a function
Andy is wrapping gifts for his family. He ties 25 inches of ribbon around each gift. Which function gives the relationship between the number of
gifts (g) and the length of ribbon used (9)?
The function representing the relationship between the length of ribbon and the number of gifts is ?

Answers
I would give an explanation but you seem in a hurry! Have a good day and good luck!
the random variable x is known to be uniformly distributed between 70 and 90. the probability of x having a value between 80 to 95 is group of answer choices 0.05 0.5 0.75 1
Answers
The probability of x having a value between 80 to 95 is 0.75.
The probability of x having a value between 80 to 95 can be determined by calculating the proportion of the total range of x that falls within that interval. Since x is uniformly distributed between 70 and 90, the probability can be obtained by dividing the width of the desired interval (15) by the width of the entire range of x (90 - 70 = 20).
Using the formula for probability in a uniform distribution, we have:
Probability = (width of interval) / (width of range)
Probability = 15 / 20
Probability = 0.75
Therefore, the probability of x having a value between 80 to 95 is 0.75.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
The random variable x is known to be uniformly distributed between 70 and 90. the probability of x having a value between 80 to 95 is group of answer choices (a)0.05 (b)0.5 (c)0.75 (d)1
Find the TWO integers whos product is -12 and whose sum is 1
Answers
Answer:
\( \rm Numbers = 4 \ and \ -3.\)
Step-by-step explanation:
Given :-
The sum of two numbers is 1 .
The product of the nos . is 12 .
And we need to find out the numbers. So let us take ,
First number be x
Second number be 1-x .
According to first condition :-
\(\rm\implies 1st \ number * 2nd \ number= -12\\\\\rm\implies x(1-x)=-12\\\\\rm\implies x - x^2=-12\\\\\rm\implies x^2-x-12=0\\\\\rm\implies x^2-4x+3x-12=0\\\\\rm\implies x(x-4)+3(x-4)=0\\\\\rm\implies (x-4)(x+3)=0\\\\\rm\implies\boxed{\red{\rm x = 4 , -3 }}\)
Hence the numbers are 4 and -3
Let integers be x and x-1
ATQ
x+x-1=1\(\\ \sf\longmapsto 2x-1=1\)
\(\\ \sf\longmapsto 2x=1+1\)
\(\\ \sf\longmapsto 2x+2\)
\(\\ \sf\longmapsto x=\dfrac{2}{2}\)
\(\\ \sf\longmapsto x=1\)
Now
\(\\ \sf\longmapsto x-1=1-1=0\)
The integers are 1 and 0But
Integers can be x and 1-x as their sum is 1
\(\\ \sf\longmapsto x(1-x)=-12\)
\(\\ \sf\longmapsto x- x^2=-12\)
\(\\ \sf\longmapsto x^2-x-12=0\)
\(\\ \sf\longmapsto x^2-4x+3x-12=0\)
\(\\ \sf\longmapsto x(x-4)+3(x-4)=0\)
\(\\ \sf\longmapsto (x-4)(x+3)=0\)
\(\\ \sf\longmapsto x=4,-3\)