A laboratory tested 82 chicken eggs and found that the mean amount of cholesterol was 228 milligrams with a = 19. 0 milligrams. Construct a 95% confidence interval for the
true mean cholesterol content,, of all such eggs.
Answers
We can say with 95% confidence that the true mean cholesterol content of all such eggs is between 223.99 milligrams and 232.01 milligrams.
To construct a 95% confidence interval for the true mean cholesterol content of all such eggs, we can use the following formula:
CI = X ± Zα/2 * σ/√n
where:
X = sample mean = 228 milligrams
Zα/2 = the critical value from the standard normal distribution corresponding to a 95% confidence level, which is 1.96
σ = population standard deviation = 19.0 milligrams
n = sample size = 82
Substituting the values into the formula, we get:
CI = 228 ± 1.96 * 19.0/√82
= 228 ± 4.01
= (223.99, 232.01)
Therefore, we can say with 95% confidence that the true mean cholesterol content of all such eggs is between 223.99 milligrams and 232.01 milligrams.
To learn more about milligrams visit:
https://brainly.com/question/29271037
#SPJ11
Related Questions
Circle a is congruent to circle j. chords bc, cf, eg, kl, lo, and mp are congruent. circles a and j are congruent. chords b c, c f, e g, k l, l o, and m p are congruent. which arcs are congruent? check all that apply. arc b c ≅ arc m p arc b c ≅ arc m o arc c f ≅ arc k p arc e g ≅ arc k l arc l o ≅ arc m p
Answers
If Circle A is congruent to circle J, then the arcs that are congruent are (1) Arc BC ≅ Arc MP, (4) Arc EG ≅ Arc KL, and (5) Arc LO ≅ Arc MP.
Two arcs in a circle are congruent if they have the same length or measure. Two arcs are congruent if and only if they subtend the same angle at the center of the circle.
In Option(1) : Arc BC and Arc MP are congruent because the chords BC and MP are congruent and subtend the same angle in their respective circles.
In Option (4) : Arc EG and Arc KL are congruent because the chords EG and KL are congruent and subtend the same angle in their respective circles.
In Option(5) : Arc LO and Arc MP are congruent because the chords LO and MP are congruent and subtend the same angle in their respective circles.
Therefore, the correct options are (1), (4) and (5).
Learn more about Arc here
https://brainly.com/question/12611897
#SPJ4
The given question is incomplete, the complete question is
Circle A is congruent to circle J. Chords BC, CF, EG, KL, LO, and MP are congruent. Which arcs are congruent? Check all that apply.
(1) Arc BC ≅ Arc MP
(2) Arc BC ≅ Arc MO
(3) Arc CF ≅ Arc KP
(4) Arc EG ≅ Arc KL
(5) Arc LO ≅ Arc MP

PLS HELP!!
Select all the correct answers
Youre given two side lengths of 3 centimeters and 5 centimeters, which measurement can you use for the length of the third side to construct a
valled triangle?
8 cm
6 cm
4 cm
10 cm
2 cm
Answers
Answer: 10
Step-by-step explanation:
Write the decimal as a fraction in simplest form.
5. -18.04
Answers
Answer: - \(\frac{451}{25}\)
Step-by-step explanation:
WILL MARK BRAINLIEST PLEASE HELP thanksss
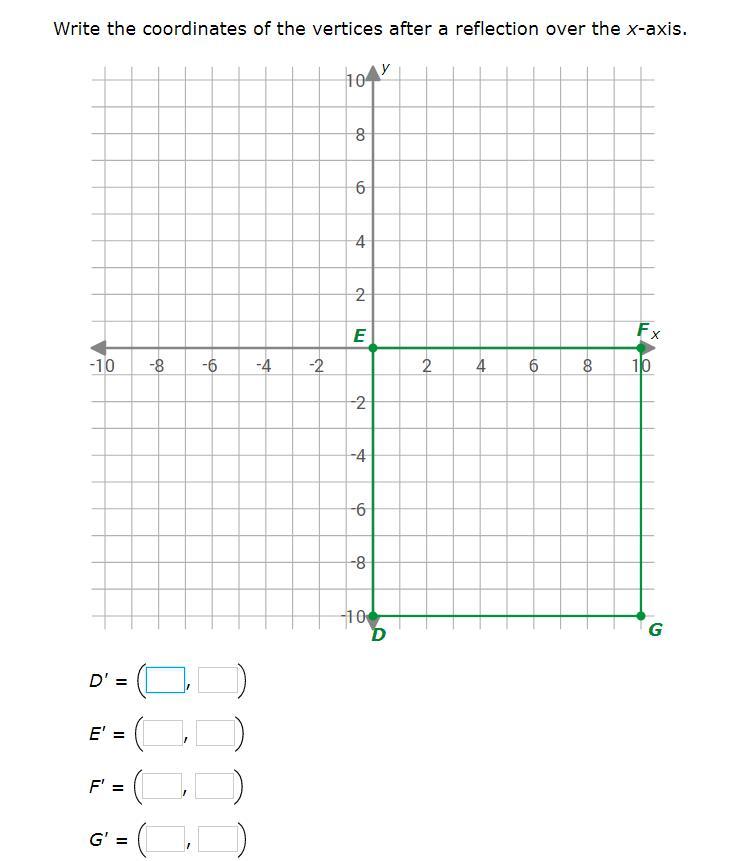
Answers
Answer:
E (0,0)
F (10,0)
D (0,10)
G (10,10)
Hope this helps!
An experiment to compare the spreading rates of five different brands of yellow interior latex paint available in a particular area used 4 gallons (J = 4) of each paint. The sample average spreading rates (ft2/gal) for the five brands were x1. = 462.0, x2. = 502.8, x3. = 427.5, x4. = 469.3, and x5. = 532.1. The computed value of F was found to be significant at level α = 0.05. With MSE = 450.8, use Tukey's procedure to investigate significant differences between brands. (Round your answer to two decimal places.)
W= ?
Which means differ significantly from one another? (Select all that apply.)
Which means differ significantly from one another? (Select all that apply.)x1. and x2.
x1. and x3.
x1. and x4.
x1. and x5.
x2. and x3.
x2. and x4.
x2. and x5.
x3. and x4.
x3. and x5.
x4. and x5.
There are no significant differences.
Answers
x1 and x2, x1 and x5, x2 and x3, x2 and x5, x3 and x4 and x3 and x5 means differ significantly from one another
The experiment to compare the spreading rates of five different brands of yellow interior latex paint available in a particular area used 4 gallons (J = 4) of each paint.
The value of W for Tukey's procedure is:
W = q(α, 5, 20) * √(MSE/J)
where α = 0.05 is the significance level, 5 is the number of treatments, 20 is the total number of observations (4 observations per treatment), MSE = 450.8 is the mean square error, and q(α, 5, 20) is the critical value from the Studentized range distribution table.
Using the table, we find that q(α, 5, 20) = 3.365.
Substituting the values, we get:
W = 3.365 * √(450.8/4) = 21.63
The means that differ significantly from one another are:
x1 and x2
x1 and x5
x2 and x3
x2 and x5
x3 and x4
x3 and x5
Therefore, the correct answer is:
x1 and x2
x1 and x5
x2 and x3
x2 and x5
x3 and x4
x3 and x5
For similar question on differ significant:
https://brainly.com/question/29603883
#SPJ11
You are working on a stop and wait ARQ system where the probability of bit error is 0.001. Your design lead has told you that the maximum reduction in efficiency due to errors that she will accept is 75% of the error free efficiency. What is the maximum frame length your system can support and still meet this target?
Answers
This can be expressed as (1 - (1 - 0.001)^N) ≤ 0.25. Solving this equation will give us the maximum frame length N that satisfies the target efficiency reduction of 75%.
In a stop-and-wait ARQ (Automatic Repeat Request) system, the sender transmits a frame and waits for an acknowledgment from the receiver before sending the next frame. To determine the maximum frame length, we need to consider the effect of bit errors on the system's efficiency.
The probability of bit error is given as 0.001, which means that for every 1000 bits transmitted, approximately one bit will be received incorrectly. The efficiency of the system is affected by the need for retransmissions when errors occur.
To meet the target efficiency reduction of 75%, we must ensure that the system's efficiency remains at least 25% of the error-free efficiency. In other words, the number of retransmissions should not exceed 25% of the frames transmitted.
Assuming a frame length of N bits, the probability of an error-free frame is (1 - 0.001)^N. Therefore, the probability of an error occurring is 1 - (1 - 0.001)^N. The number of retransmissions is directly proportional to the probability of errors.
To meet the target, the number of retransmissions should be less than or equal to 25% of the total frames transmitted. Mathematically, this can be expressed as (1 - (1 - 0.001)^N) ≤ 0.25. Solving this equation will give us the maximum frame length N that satisfies the target efficiency reduction of 75%.
For more information on probability visit: brainly.com/question/33170251
#SPJ11
What is the equation?

Answers
Answer:
(x - 7)^2 + (y - 2)^2 = 5^2
Step-by-step explanation:
Center at (7, 2); radius 5
Adapt (x - h)^2 + (y - k)^2 = r^2 to this situation. Replace h by 7, k by 2 and r by 5:
(x - 7)^2 + (y - 2)^2 = 5^2
Here are the first four terms of an arithmetic sequence. 3 10 17 24 Find, in terms of n, an expression for the nth term of this arithmetic sequence.
Answers
Answer:
\(a_{n}\) = 7n - 4
Step-by-step explanation:
The n th term of an arithmetic sequence is
\(a_{n}\) = a₁ + (n - 1)d
where a₁ is the first term and d the common difference
Here a₁ = 3 and d = a₂ - a₁ = 10 - 3 = 7 , thus
\(a_{n}\) = 3 + 7(n - 1) = 3 + 7n - 7 = 7n - 4
If K is the midpoint of JL, JK=8x+11 and KL=14x-1, find JL.
Answers
Given that K is the midpoint on segment JL, the numerical value of segment JL is 54.
What is the numerical value of segment JL?A midpoint is simply a point that divides a segment into two equal halves.
Given the data in the question;
K is the midpoint on segment JLSegment JK = 8x + 11 Segment KL= 14x - 1Numerical value of segment JL = ?Given that K is the midpoint on segment JL, this means segment JK is divided into two equal halves, Segment JK is equal to Segment KL.
Segment JK = Segment KL
8x + 11 = 14x - 1
Collect like terms
8x - 14x = -1 - 11
-6x = -12
x = -12/-6
x = 2
Hence, the numerical values of Segment JK and Segment KL will be;
Segment JK = 8x + 11 = 8(2) + 11 = 16 + 11 = 27
Segment KL = 14x - 1 = 14(2) - 1 = 28 - 1 = 27
Since Segment JK and Segment KL makes up segment JL, the numerical value of Segment JL is the sum of Segment JK and Segment KL.
Segment JL = 27 + 27 = 54
Given that K is the midpoint on segment JL, the numerical value of segment JL is 54.
Learn more about midpoint here: https://brainly.com/question/4747771
#SPJ1
Given triangle DOG is congruent to triangle CAT, which reason could you use to prove that angle G is congruent to angle T?

Answers
Answer:
The correct option is;
d) CPCTC
Step-by-step explanation:
The phrase Corresponding Parts of Congruent Triangles are Congruent with the acronym CPCTC, is used as valid reasoning in the provision of a proof, after the existence of congruency between two triangles has been proven
Given that the triangles ΔDOG and ΔCAT have been proven congruent, we have that the corresponding vertices are;
Vertex D corresponds to vertex C
Vertex O corresponds to vertex A
Vertex G corresponds to vertex T
Therefore, given that ΔDOG ≅ ΔCAT, we have;
∠D ≅ ∠C by CPCTC
∠O ≅ ∠A by CPCTC
∠G ≅ ∠T by CPCTC.
Problem 1 Show by explicit substitution that E=cos(kz−ωt) is a solution to the 'wave equation' ∂t2∂2E−c2∂z2∂2E=0, noting that k2ω2=c2. Problem 2: A plane light wave travels in the z-direction with Emag=1000i^ V/m. It has a frequency ω=1015rad/s. What is Bmag ? What is the average intensity, Savg, of this light wave in watts per square meter? If the frequency of the wave were doubled, how would either … or Savg change?
Answers
E = cos(kz - ωt) is a solution to the wave equation. Bmag = 1000i / 3 x 10⁸ = 3.33 x 10⁻⁶i T/m.
By explicit substitution, we need to verify that E = cos (kz - ωt) is a solution to the wave equation:∂²E/∂t² - c² ∂²E/∂z² = 0Given k²ω² = c², we have the following relationships: k = ± ω/c and ω = kc.
Substituting E = cos(kz - ωt) into the wave equation, we have the following:∂²E/∂t² = - ω² cos(kz - ωt)∂²E/∂z² = - k² cos(kz - ωt)Thus, the wave equation becomes: - ω² cos(kz - ωt) - c² (- k² cos(kz - ωt)) = 0.
This can be simplified as follows: ω² cos(kz - ωt) + c²k² cos(kz - ωt) = 0Multiplying both sides by cos(kz - ωt), we get: (ω² + c²k²) cos(kz - ωt) = 0.
Since cos(kz - ωt) ≠ 0, we must have:ω² + c²k² = 0 ⇒ ω² = - c²k²Therefore, E = cos(kz - ωt) is a solution to the wave equation.
Given Emag = 1000i V/m, ω = 10¹⁵ rad/s. We need to find Bmag and Savg.Using the relationship: c = fλ, we have:ω = 2πf, so f = ω/2πTherefore, c = ωλ/2π, so λ = 2πc/ωSince v = fλ, we have v = c
Hence, Emag/Bmag = c ⇒ Bmag = Emag/c= 1000i / 3 x 10⁸ = 3.33 x 10⁻⁶i T/mSavg = ½ ε₀ c Emag²where ε₀ is the permittivity of free space.
Thus, we have: Savg = ½ (8.85 x 10⁻¹²) (3 x 10⁸) (1000)²= 1.32 x 10⁻³ W/m²If the frequency is doubled, ω → 2ω, so λ → λ/2 and Emag → 2Emag. Hence, Bmag → 2Bmag, andSavg → 4Savg.
Thus, either Bmag or Savg increases by a factor of 2
The given wave equation is ∂²E/∂t² - c² ∂²E/∂z² = 0. We need to show that E = cos(kz - ωt) is a solution to this wave equation.
Using the relationships k²ω² = c² and ω = kc, we obtain k = ± ω/c.
Substituting E = cos(kz - ωt) into the wave equation, we get ∂²E/∂t² = - ω² cos(kz - ωt) and ∂²E/∂z² = - k² cos(kz - ωt).
Thus, the wave equation becomes - ω² cos(kz - ωt) - c² (- k² cos(kz - ωt)) = 0, which simplifies to ω² cos(kz - ωt) + c²k² cos(kz - ωt) = 0.
Multiplying both sides by cos(kz - ωt), we get (ω² + c²k²) cos(kz - ωt) = 0. Since cos(kz - ωt) ≠ 0, we must have ω² + c²k² = 0 ⇒ ω² = - c²k².
Therefore, E = cos(kz - ωt) is a solution to the wave equation. In problem 2, we are given Emag = 1000i V/m, ω = 10¹⁵ rad/s.
To find Bmag, we use the relationship Bmag = Emag/c. Since c = 3 x 10⁸ m/s, we obtain Bmag = 1000i / 3 x 10⁸ = 3.33 x 10⁻⁶i T/m.
To find Savg, we use the relationship Savg = ½ ε₀ c Emag², where ε₀ is the permittivity of free space.
Substituting the given values, we get Savg = ½ (8.85 x 10⁻¹²) (3 x 10⁸) (1000)² = 1.32 x 10⁻³ W/m².
If the frequency of the wave were doubled, ω → 2ω, so λ → λ/2 and Emag → 2Emag. Hence, Bmag → 2Bmag, and Savg → 4Savg.
Thus, either Bmag or Savg increases by a factor of 2.
In conclusion, E = cos(kz - ωt) is a solution to the wave equation ∂²E/∂t² - c² ∂²E/∂z² = 0, where k²ω² = c². For a plane light wave with Emag = 1000i V/m and ω = 10¹⁵ rad/s, we found that Bmag = 3.33 x 10⁻⁶i T/m and Savg = 1.32 x 10⁻³ W/m². If the frequency of the wave were doubled, either Bmag or Savg would increase by a factor of 2.
To know more about permittivity of free space visit:
brainly.com/question/30403318
#SPJ11
Which of the following is a point of tangency on the circle below?
Pls answer ASAP

Answers
Answer:
Point Z
Step-by-step explanation:
The definition of a tangent is a line that is outside of a circle that touches the circle at only one point. W is the tangent to this circle, and the point where they meet is point Z.
Answer: point z
Step-by-step explanation:
I just took the test
Find the area. :)
please and thx

Answers
Answer:
132 cm²
Step-by-step explanation:
To find the area of the figure, start by dividing the figure into smaller rectangles.
Area of figure
= area of shaded rectangle +area of unshaded rectangle
\(\textcolor{steelblue}{\text{Area of rectangle= length ×breadth}}\)
Shaded rectangle
Length= 4 cm
Breadth= 6 cm
Area
= 4(6)
= 24 cm²
Unshaded rectangle
Length= 9 cm
Breadth= 12 cm
Area
= 9(12)
= 108 cm²
After finding the area of each rectangle, we can add the two areas together to obtain the total area of the figure.
Area of figure
= 108 +24
= 132 cm²

A bakery sells chocolate cupcakes and mocha cupcakes. It sold 500 cupcakes in a day, and 16% of them were mocha. How many of the cupcakes sold that day were chocolate?
Answers
Answer:
Your answer
420 were chocolate
Mark it as Brainlist. Follow me for more answer.
Step-by-step explanation:
of a pizza remains, and Seth and Ethan want to split it evenly. What fraction of the original pizza will each get?
Answers
Answer:
\(\huge\boxed{\text{Multiply the denominator by 2, or}}\\\\\huge{\boxed{\text{divide the percentage by 2}}}}\)
Step-by-step explanation:
Because there is no fraction or percentage given, simply follow this rule to divide a portion by 2.
Hope it helps :) and let me know if you want me to elaborate(solve with fraction)
Shawn bought $45.00 worth of pencils from Office Max. If the sales tax is 4%, what was the amount of tax she had to pay?
Answers
Answer:
46.80
Step-by-step explanation:
because 45/4%=1.80 and 45+1.80=46.80
The numbers 1 through 10 are
written on individual cards and
placed in a bag. If you reach
into the bag and grab one card,
what is the probability that you
will grab the number 2 card?
Answers
Answer:
1/10
Step-by-step explanation:
SInce there are a total of 10 cards and only one card with the number 2, then out of the ten cards you only have a 1/10 chance of grabbing the number 2 card! Hope this helps :)
Consider a multiple channel line with 5 cashiers. The customer arrival rate, $\lambda$, is $85.5 /$ hour, and the service rate, $\mu$, is $19 /$ hour. Determine the average waiting time in minutes. (Round your answer to TWO places of decimal) \#5.
Answers
The average waiting time in minutes is approximately 0.317 minutes.
To determine the average waiting time in minutes, we can use the queuing theory formula for average waiting time in an\($\mathrm{M} / \mathrm{M} / \mathrm{c}$\) queue:
\($$W_q=\frac{\rho^{c+1}}{c ! \cdot(1-\rho)} \cdot \frac{1}{\mu-\lambda}$$\)
Where:
\($W_q$\) is the average waiting time in the queue.
\($\rho$\) is the traffic intensity, given by $\frac{\lambda}{c \cdot \mu}$.
\($c$\) is the number of service channels (cashiers).
\($\mu$\) is the service rate (customers per hour).
\($\lambda$\) is the arrival rate (customers per hour).
Given:
\($\lambda=85.5$\)customers per hour.
\($\mu=19$\) customers per hour.
\($c=5$\) cashiers.
First, let's calculate $\rho$ :
\($$\rho=\frac{\lambda}{c \mu}=\frac{85.5}{5 \cdot 19} \approx 0.9011$$\)
Now, let's calculate \($W_q$\) :
\($$W_q=\frac{\rho^{c+1}}{c ! \cdot(1-\rho)} \cdot \frac{1}{\mu-\lambda}\\=\frac{0.9011^{5+1}}{5 ! \cdot(1-0.9011)} \cdot \frac{1}{19-85.5} \\\approx 0.317 \text { (rounded to two decimal places) }$$\)
Therefore,the average waiting time in minutes is approximately 0.317 minutes.
learn more about interest expense on
https://brainly.com/question/24057012
#SPJ11
Please explain your answer, I need to upload notes.

Answers
Answer:
Step-by-step explanation:
well the x is 1/1 and the 2 is over 1 so divided and it is B is what i got
Carlos drove 1,064 miles on his vacation. He drove a total of 20 hours. What is the average number of miles Carlos drove each hour? Group of answer choices
Answers
Given a collection of 2023 closed squares of total area 4, prove that they can be arranged to cover a unit square (overlaps are allowed)
Answers
We can arrange the 2023 squares to cover the unit square, with overlaps allowed.
We can prove that a collection of 2023 closed squares of total area 4 can be arranged to cover a unit square by using the pigeonhole principle. Since the total area of the squares is 4, the average area of each square is 4/2023. Let's take a unit square and divide it into 2023 smaller squares of area (1/2023) each. By the pigeonhole principle, we can assign one of the 2023 squares to each of the smaller squares. Since the average area of each square is 4/2023, each of the assigned squares will overlap with at most 4 other squares. Therefore, we can arrange the 2023 squares to cover the unit square, with overlaps allowed.
Learn more about the pigeonhole principle here: brainly.com/question/30322724
#SPJ4
Which value for x makes this sentence true? ( 8th Grade math )

Answers
Answer:
C. x = 5
Step-by-step explanation:
\(2x - 1 = 9\)
\(2x = 9 + 1\)
\(2x = 10\)
\(x = 5\)
Bill had a $7 coupon for the purchase of any item. He bought a dvd recorder that was on sale forlu
of its original price. After using the coupon, Bill paid $86 for the dvd recorder before taxes. What
was the original price of the dvd recorder?
Answers
Answer:
5 maybe
Step-by-step explanation:
Rahul has $720 to spend at a bicycle store for some new gear and biking outfits. Assume all prices listed include tax.He buys a new bicycle for $378.51.He buys 2 bicycle reflectors for $10.51 each and a pair of bike gloves for $29.74.He plans to spend some or all of the money he has left to buy new biking outfits for $55.16 each.What is the greatest number of outfits Rahul can buy with the money that's left over?
Answers
Given :
The amount with Rahul is $720.
The cost of new bicycle is $378.51.
The cost of 2 bicycle reflectors is
\(2\times10.51=21.02dollar\)The cost of pair of bike gloves is $29.74.
The cost of new biking outfit is $55.16.
Explanation :
Let the number of outfits be x.
Then the inequality formed is
\(720\leq378.51+21.02+29.74+55.16x\)\(720\leq429.27+55.16x\)\(\begin{gathered} 290.73\leq55.16x \\ 5.27\leq x \\ x\leq5.27 \end{gathered}\)Answer:
Hence the greatest number of outfits Rahul can buy with the money that's left over is 5.
find the area of the surface defined by x + y + z = 1, x2 + 7y2 ≤ 1.
Answers
The area of the surface is (2/3)π.
We can solve this problem using a double integral. First, we need to find the limits of integration for x and y. From the equation x + y + z = 1, we get:
z = 1 - x - y
Substituting this into the equation x² + 7y² ≤ 1, we get:
x² + 7y² ≤ 1 - z² + 2xz + 2yz
Since we want to find the area of the surface, we need to integrate over x and y for each value of z that satisfies this inequality. The limits of integration for x and y are given by the ellipse x² + 7y² ≤ 1 - z² + 2xz + 2yz, so we can write:
∫∫[x² + 7y² ≤ 1 - z² + 2xz + 2yz] dA
where dA is the area element.
To evaluate this integral, we can change to elliptical coordinates u and v, defined by:
x = √(1 - z²) cos u
y = 1/√7 √(1 - z²) sin u
z = v
The limits of integration for u and v are:
0 ≤ u ≤ 2π
-1 ≤ v ≤ 1
The Jacobian for this transformation is:
J = √(1 - z²)/√7
So the integral becomes:
∫∫[u,v] (x² + 7y² )J du dv
Substituting in the values for x, y, z, and J, we get:
∫∫[u,v] [(1 - z²) cos² u + 7/7 (1 - z²) sin² u] √(1 - z²)/√7 du dv
Simplifying, we get:
∫∫[u,v] [(1 - z²) (cos² u + sin² u)] (1/√7) dz du dv
= ∫∫[u,v] [(1 - z²)/√7] dz du dv
= (2/3)π
Therefore, the area of the surface defined by x + y + z = 1, x² + 7y² ≤ 1 is (2/3)π.
To learn more about double integral here:
brainly.com/question/29754607#
#SPJ11
Which are correct representations of the inequality –3(2x – 5) < 5(2 – x)? Select two options. x < 5 –6x – 5 < 10 – x –6x + 15 < 10 – 5x A number line from negative 3 to 3 in increments of 1. An open circle is at 5 and a bold line starts at 5 and is pointing to the right. A number line from negative 3 to 3 in increments of 1. An open circle is at negative 5 and a bold line starts at negative 5 and is pointing to the left.
Answers
The correct representations of the inequality is
- 6x + 15 < 10 - 5x and An open circle is at 5 and a bold line starts at 5 and is pointing to the right.
We have the inequality -3(2x - 5) < 5(2 - x)
Now, simplifying each side of inequality
-3(2x - 5) = -3(2x) + -3(-5)
-3(2x - 5) = - 6x + 15
and, 5(2 - x) = 5(2) + 5(-x)
5(2 - x) = 10 - 5x
So, - 6x + 15 < 10 - 5x
Now, Subtract 15 from both sides
- 6x < -5 - 5x
- x < - 5
x > 5
The correct statements are:
- 6x + 15 < 10 - 5x and An open circle is at 5 and a bold line starts at 5 and is pointing to the right.
Learn more about Inequality here:
https://brainly.com/question/30228778
#SPJ1
How do you find the y-intercept with two ordered pairs?
Answers
Equation employing the slope-intercept method for two points
The slope-intercept version of the equation may be used to calculate the two-point Y-intercept.
The shape of a point-slope is\(\mathbf{Y-Y_{1} = m(X-X_{1})}.\)
Steps to find the y-intercept with two ordered pairs?
Determine the slope using two points.
\(Slope = \frac{Y_{2}-Y_{1}}{X_{2}-X_{1}} = \frac{Rise}{Run} = \frac{\bigtriangleup Y}{\bigtriangleup X}\)
As an illustration, two points are (3, 5) and (6, 11)
Slope = \(\frac{Y_{2}-Y_{1}}{X_{2}-X_{1}} = \frac{11 - 5}{6 - 3} = \frac{6}{3} = 2\)
In the slope-intercept form of the equation, substitute the slope(m).
\(\\y = mx+b \\y = 2x+b\)
Either point may be substituted in the equation. You may either use (3,5) or (6,11).
\(\\y = 2x+b \\5 = 2(3)+b\)
Find the answer to the equation for b, the line's y-intercept.
\(\\5 \ \ \ = 2(3) + b \\5 \ \ \ = 6 + b \\\underline{-6\ = -6 \ \ \ \ \ \ \ } \\-1 = b\)
Substitute b, into the equation.
\(\\y = 2x + b \\y = 2x - 1\)
Learn more about y-intercept with two ordered pairs from the link below
https://brainly.com/question/10708360
#SPJ4
What is an expression for the radius of the circle? What is the least possible integer value of x for the circle to exist? Explain

Answers
The area of a circle is given by the next formula:
\(A=\pi *r^2\)___________
For the given expression of area:
\(\pi *r^2=4\pi x^2+12\pi x+9\pi\)Use the equation above to solve r (radius):
1. Divide both sides of the equation into π
\(\begin{gathered} \frac{\pi *r^2}{\pi}=\frac{4\pi x^2+12\pi x+9\pi}{\pi} \\ \\ r^2=4x^2+12x+9 \end{gathered}\)2. Factor the expression on the right using the notable product perfect square binomial:
\(\begin{gathered} (a+b)\placeholder{⬚}^2=a^2+2ab+b^2 \\ \\ 4x^2+12x+9=(2x)\placeholder{⬚}^2+2(2x)(3)+3^2 \\ 4x^2+12x+9=(2x+3)\placeholder{⬚}^2 \\ \\ \\ r^2=(2x+3)\placeholder{⬚}^2 \end{gathered}\)3. Find square root of both sides of the equation:
\(\begin{gathered} \sqrt{r^2}=\sqrt{(2x+3)\placeholder{⬚}^2} \\ \\ r=2x+3 \end{gathered}\)Then, the radius is given by the expression 2x+3.______________________________
To find the least possible integer value of x: As r is the radius of a circle, it cannot be a negative amount or 0, then r needs to be greather than 0:
\(\begin{gathered} 2x+3>0 \\ \end{gathered}\)Solve the ineqaulity above:
\(\begin{gathered} 2x+3-3>0-3 \\ 2x>-3 \\ \\ \frac{2x}{2}>-\frac{3}{2} \\ \\ x>-\frac{3}{2} \end{gathered}\)x needs to be greater than -3/2 (-1.5).
Then, the least possible integer value of x is -1Answer:
450
Step-by-step explanation:
calculate it by solving the radius as you get the radius you will be able to do th question
Two angles are complementary. The larger one is 3 times the measure of the
smaller one. What is the measure of the smaller angle in degrees?
Type just the numerical value.
Answers
Answer: 22.5°
Step-by-step explanation:
Complementary angles are the angles that when we add them together, they're equal to 90°.
Let the smaller angle be represented by x.
Then, the larger one will be 3 × x = 3x
We then add both angles together and equate them to 90°. Therefore,
x + 3x = 90°
4x = 90°
x = 90/4
x = 22.5°
The smaller angle is 22.5°
Debora deposits $5000 into a savings account. The bank promises to provide an annual interest rate of 5%, compounded yearly. Assuming that Debora keeps the money in her bank account and does not withdraw any funds, calculate the value of her investment after 10 years
Answers
After 10 years, Debora's investment of $5000 in the savings account with a 5% annual interest rate, compounded yearly, will grow to approximately $6,633.16.
To calculate the value of Debora's investment after 10 years, we can use the formula for compound interest:
\(A = P(1 + r/n)^(nt)\)
Where:
A is the final amount (the value of the investment after the given time period)
P is the principal amount (the initial deposit)
r is the annual interest rate (expressed as a decimal)
n is the number of times interest is compounded per year
t is the number of years
In this case, Debora deposits $5000 into the savings account with an annual interest rate of 5%, compounded yearly. Plugging in the values into the formula:
\(A = 5000(1 + 0.05/1)^(1*10)\)
Simplifying the calculation:
\(A = 5000(1.05)^10\)
Using a calculator or computing the value iteratively, we find:
A ≈ 5000 * 1.628895
A ≈ 6,633.16
Therefore, after 10 years, Debora's investment of $5000 in the savings account will grow to approximately $6,633.16. This means that the investment will accumulate approximately $1,633.16 in interest over the 10-year period, given the 5% annual interest rate compounded yearly.
Learn more about compound interest here:
https://brainly.com/question/13155407
#SPJ11