A kayak rental company charges $25.00 to rent a kayak and $3.50 for each half hour it is used. Which linear function best represents the total cost of renting a kayak for 4 hours?
Answers
Answer:
y = 25 + 3.5x, where x is a half hour
y = 25 + 3.5 (4 * 2) = $53
Step-by-step explanation:
Related Questions
An Austrian study was completed to determine if untrained sea lions and sea lionesses could follow various experimenter-given cues when given a choice of two objects. One experimenter-given cue was to point at one of the objects. One sea lioness, named Zwerg, successfully chose the pointed-at object 37 times out of 48 trials. Does this result show that Zwerg can correctly follow this type of direction by an experimenter more than 50% of the time?ââ
Answers
Using the z-distribution, it is found that since the test statistic is greater than the critical value for the right-tailed test, this result shows that Zwerg can correctly follow this type of direction by an experimenter more than 50% of the time.
What are the hypothesis?At the null hypothesis, it is tested if Zwerg cannot correctly follow this type of direction by an experimenter more than 50% of the time, that is:\(H_0: p \leq 0.5\)
At the alternative hypothesis, it is tested if Zwerg can correctly follow this type of direction by an experimenter more than 50% of the time, that is:\(H_1: p > 0.5\)
Test statisticThe test statistic is given by:
\(z = \frac{\overline{p} - p}{\sqrt{\frac{p(1-p)}{n}}}\)
In which:
\(\overline{p}\) is the sample proportion.p is the proportion tested at the null hypothesis.n is the sample size.For this problem, the parameters are:
\(n = 48, \overline{p} = \frac{37}{48} = 0.7708, p = 0.5\)
The value of the test statistic is:
\(z = \frac{\overline{p} - p}{\sqrt{\frac{p(1-p)}{n}}}\)
\(z = \frac{0.7708 - 0.5}{\sqrt{\frac{0.5(0.5)}{48}}}\)
\(z = 3.75\)
Considering a right-tailed test, as we are testing if the proportion is greater than a value, with a significance level of 0.05, the critical value for the z-distribution is \(z^{\ast} = 1.645\).
Since the test statistic is greater than the critical value for the right-tailed test, this result shows that Zwerg can correctly follow this type of direction by an experimenter more than 50% of the time.
To learn more about the z-distribution, you can take a look at https://brainly.com/question/16313918
help me bc a b is stupid...

Answers
Answer:
8cm³
Step-by-step explanation:
This is a problem finding volume through water displacement.
When you drop an object in water, its volume is the change in the height of the water.
In picture two the height of the water is at 25, and in picture one the height is at 17.
25-17=8
Simplify the expression. Write your answer as a power.

Answers
When multiplying two powers, if their bases are the same, then you simply add the exponents:
\(\frac{8^5*8^3*8^2}{8^8} =\frac{8^{5+3+2}}{8^8} =\frac{8^{10}}{8^8}\)
When dividing two powers, if their bases are the same, you simply minus the exponents.
\(\frac{8^{10}}{8^8}=8^{10-8}=8^2\)
Thus when the expression is simplified, the answer as a power is \(8^2\)
Answer: 8^2
Hope that helps!
A group of college students built a self-guided rover and tested it on a plane surface. They programmed the vehicle to move along the path Aâ€""Bâ€""Câ€""Dâ€""A represented on the coordinate plane. What distance will the rover cover if it completes one circuit?.
Answers
The distance covered by the rover is the perimeter of the trapezoid, and it is 40 meters.
See attachment for the path followed by the rover.
From the attached graph, we have the following lengths
\(AD = 9m\)
\(AB = 2m\)
\(DC = 14m\)
Next, we calculate the distance BC using the following Pythagoras theorem
\(BC^2 = AD^2 + x^2\)
Where:
\(x = 12\)
So, we have:
\(BC^2 = 9^2 + 12^2\)
\(BC^2 = 225\)
Take positive square root of both sides
\(BC = 15\)
The distance covered is the sum of the side lengths of the trapezoid.
So, we have:
\(Distance =AD + AB +DC + BC\)
This gives
\(Distance =9m+ 2m +14m + 15m\)
Add the lengths
\(Distance =40m\)
Hence, the distance covered by the rover is 40 meters
Read more about distance at:
https://brainly.com/question/13136492

Brainliest if correct please help
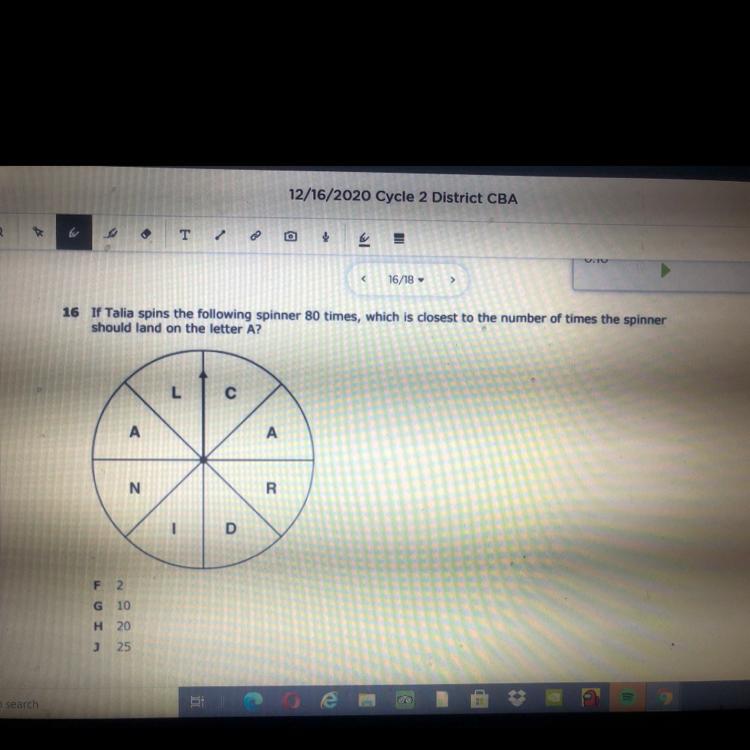
Answers
Answer: 10
Step-by-step explanation: there are 8 sides and if u were to divide by 80 by 8, u would get 10
hope this helps! :)
Because if you count all the pieces, there are 8. And if you count to A it’s 2. I did 8 - 4 = 4 and 80/4=20
PLEASE HELP FIRST ANSWER GETS BRAINLIEST OR WHATEVER ITS CALLED

Answers
Answer: B
Step-by-step explanation:
y= x/5 + 3 if that helps
what is the median of these numbers 17 12 54 36 71 28 31 55
Answers
Answer:
The median is 33.5
Step-by-step explanation:
In order to solve for a median it would either be the middle or it would be the average of the middle if there are even amount of numbers. First you would put them in order. 12 17 28 31 36 54 55 and 71. This would mean the the middle number would be 31 and 36. Since you can't have two medians you would find the average of the two so add 31 and 36 which would be equal to 67 then divide by 2 which would equal to 33.5.
The median of numbers 17, 12, 54, 36, 71, 28, 31, 55 is 33.5.
What is the median of a set of numbers?The median of a set of numbers is the middle value when the numbers are arranged in ascending or descending order.
If there are an even number of numbers, the median is the average of the two middle values. If there is an odd number of numbers, the median is the middle number.
To find the median of the given numbers, we first need to arrange them in ascending order:
12 17 28 31 36 54 55 71
Since there are an even number of numbers (8), the median will be the average of the two middle values, which are 31 and 36.
To find the average, we add the two numbers and divide by 2:
(31 + 36) / 2 = 67 / 2 = 33.5
Therefore, the median of the given numbers is 33.5.
Learn more about median of numbers in https://brainly.com/question/26177250
#SPJ11
John's commute time to work during the week follows the normal probability distribution with a mean time of 26.7 minutes and a standard deviation of 5.1 minutes. The interval around the mean that contains 99.7% of the commute times is ________.
Answers
The interval around the mean that contains 99.7% of the commute times is approximately 16.5 to 36.9 minutes.
In statistics, the normal probability distribution, also known as the bell curve, is commonly used to model random variables such as commute times. It is characterized by its mean (average) and standard deviation. In this case, John's commute time follows a normal distribution with a mean of 26.7 minutes and a standard deviation of 5.1 minutes.
To determine the interval that contains 99.7% of the commute times, we can use the empirical rule, also known as the 68-95-99.7 rule, which states that for a normal distribution:
- Approximately 68% of the data falls within one standard deviation of the mean.
- Approximately 95% falls within two standard deviations.
- Approximately 99.7% falls within three standard deviations.
Since we know that John's commute time is normally distributed with a mean of 26.7 minutes and a standard deviation of 5.1 minutes, we can calculate the interval as follows:
Lower bound: Mean - (\(3 * standard deviation\)) = 2\(6.7 - (3 * 5.1) = 26.7 - 15.3 = 11.4 minutes\)
Upper bound: Mean + (\(3 * standard deviation\)) = 2\(6.7 + (3 * 5.1) = 26.7 + 15.3 = 42 minutes\)
Therefore, the interval around the mean that contains 99.7% of John's commute times is approximately 11.4 to 42 minutes.
Learn more about probability distribution
brainly.com/question/29062095
#SPJ11
Tracy wants to make 4 curtains. Each requires 54 yards of fabric. How
much fabric does she need?
Pls helpppp!!!!

Answers
Answer:
21 yards
Step-by-step explanation:
4*21/4
84/4
21
Answer:
21yards multiplication
Step-by-step explanation:
Given parameters:
Number of curtains = 4
Amount of fabric needed = \(5\frac{1}{4}\)yards
Unknown:
How much of fabric is needed = ?
Solution:
A curtain requires \(5\frac{1}{4}\)yards = \(\frac{21}{4}\)yards
Now to make 4 curtains, we would need \(\frac{21}{4}\) x 4 = 21yards.
2 1/3 - 1 1/2
Answer this for 15 points
Answers
Answer:
5/6
Step-by-step explanation:
2 1/3=2 2/6
1 1/2= 1 3/6
2 2/6- 1 3/6=5/6
Answer:
The answer is -19/6
Step-by-step explanation:
Hope that helps!
Rewrite the following equation in slope-intercept form. Y + 5 = 1 7 ( x + 7 )
Answers
Answer: y = 17x + 114
Step-by-step explanation:
The equation for the slope-intercept form is y = mx + b.
Arrange the equation so that it resembles y = mx + b.
You will do this by multiplying and subtracting so y is on the left side of the equation and mx + b is on the right side of the equation.
y + 5 = 17(x + 7)
y + 5 = 17x + 119
y + 5 - 5 = 17x + 119 - 5
y = 17x + 114
Answer:
Y = 17x + 114
Step-by-step explanation:
1. Y + 5 = 17 (x+7)
2. Y + 5 = 17x + 119 [Multiply the numbers in parenthesis by 17.]
3. Y = 17x + 114. [To keep the balance and move the 5 over, subtract it from 119.]
Assume that y varies inversely as x. If y is 2.4 when x = 5, which is an equation that relates x and y?
A. (y/x) = (25/12)
B. y = 7.4 − x
C. y = + 2.2
D. xy = 12
Answers
The equation that relates x and y is xy = 12. The solution has been obtained by using proportions.
What is proportion?
Two numbers are compared. It is known as a proportion in mathematics. The law of proportion states that if two sets of given numbers rise or decrease in the same ratio, they are considered to be directly proportionate to one another. Else, they are inversely proportion.
We are given that y varies inversely as x.
This implies that
⇒y ∝ 1/x
⇒xy = k
We are given when x = 5, y is 2.4. So, we get
⇒5 * 2.4 = k
⇒k = 12
Thus, we get xy = 12.
Hence, the equation that relates x and y is xy = 12.
Learn more about proportion from the given link
https://brainly.com/question/870035
#SPJ1
I NEED THE ANSWER FAST PLEASE!!

Answers
Answer:
1185
Step-by-step explanation:
A Parallel Line means the slope must be the same as the Given Line. A Perpendicular Line means the slope must be the negative reciprocal of the Given Line.
For Row A: Parallel is 12, Perpendicular is 6
For Row B: Parallel is 2, Perpendicular is 11
For Row C: Parallel is 9, Perpendicular is 16
For Row D: Parallel is 4, Perpendicular is 13
In Row E's case, 0 doesn't have a negative reciprocal, so you go with the equation that has a straight line down but no Y-Intercept.
For Row E: Parallel is 15, Perpendicular is 7
Row A = 72
Row B = 22
Row C = 144
Row D = 52
Row E = 105
Sum = 395
Code = 395 × 3 = 1185
The volume of a spherical balloon is 3054 cm^3. Find the surface area of the balloon to the nearest whole number.
Answers
Surface Area = 4πr²
where r is the radius of the sphere.
To find the surface area of the balloon, we first need to find the radius. We can use the formula for the volume of a sphere to find the radius:
Volume = (4/3)πr³
3054 = (4/3)πr³
r³ = 3054 x (3/4π)
r = 9
Now that we know the radius is 9 cm, we can use the formula for surface area to find the answer:
Surface Area = 4πr²
Surface Area = 4π(9)²
Surface Area ≈ 1018
Therefore, the surface area of the balloon is approximately 1018 cm².
For what value of x does 625 = 5 superscript 6 minus 2 x?
Answers
This are functions that increases geometrically. The value of x for the expression is true is 1
Exponential functionsThis are functions that increases geometrically. Given the expression below:
\(625=5^{6-2x}\)
Write both sides to the base of 5
\(5^4 = 5^{6-2x}\)
Cancel the base to have:
4 = 6 - 2x
-2x = -2
x = 1
Hence the value of x for the expression is true is 1
Learn more on indices here: https://brainly.com/question/10339517
#SPJ4
Answer:
a) 1
Step-by-step explanation:
edg 2022
Gribbles are small, pale white, marine worms that bore through wood. While sometimes considered a pest since they can wreck wooden docks and piers, they are now being studied to determine whether the enzyme they secrete will allow us to turn inedible wood and plant waste into biofuel.1 A sample of 50 gribbles finds an average length of 3.1 mm with a standard deviation of 0.72. Give a best estimate for the length of gribbles, a margin of error for this estimate (with 99% confidence), and a 99% confidence interval. Round your answer for the point estimate to one decimal place, and your answers for the margin of error and the confidence interval to two decimal places. point estimate = Enter your answer; point estimate margin of error = Enter your answer; margin of error The 99% confidence interval is Enter your answer; The 99%confidence interval, value 1 to Enter your answer; The 99%confidence interval, value 2
Answers
Answer:
a) The Margin of Error = 0.26
b) The 99% Confidence Interval = ( 2.84, 3.36)
Step-by-step explanation:
a) Margin of Error
The formula for Margin of Error =
z × Standard deviation/√n
From the above question
The z score for 99% confidence interval = 2.576
Standard deviation = 0.72
n = Random number of samples = 50
Margin of Error =
2.576 × 0.72/√50
= 1.85472 /√(50)
= 0.2622970178
Approximately to 2 decimal places = 0.26
b) 99% Confidence Interval
= Mean ± Margin of Error
Mean = 3.1mm
Confidence Interval = 3.1 ± 0.26
3.1 ± 0.26
= 2.84
3.1 + 0.26
= 3.36
The 99% Confidence Interval = ( 2.84, 3.36)
easy multiple choice!
Answers
Answer:
what are the choices
Step-by-step explanation:
Answer: is there suppose to be a pic?
A closed half-plane is the solution of a linear inequality that comes close to the boundary line.
O True
O False
Answers
Answer:false
Step-by-step explanation:
What amount of pure acid must be added to 400 mL of a 30% acid solution to produce a 75% acid solution?
Answers
Step-by-step explanation:
pure acid is a 100% acid solution.
x = ml of 100% solution
1×x + 0.3×400 = 0.75×(400 + x)
x + 120 = 300 + 0.75x
0.25x = 180
x = 720 ml
we must add 720 ml of pure acid to the 400 ml of 30% solution to create a 75% solution (1,120 ml in total).
For 23 years, Janet saved $1,150 at the beginning of every month in a fund that earned 3.25% compounded annually. a. What was the balance in the fund at the end of the period? Round to the nearest cent Round to the nearest cent b. What was the amount of interest earned over the period?
Answers
The balance in the fund at the end of 23 years, with monthly deposits of $1,150 and a 3.25% annual interest rate, is approximately $449,069.51. The amount of interest earned over the period is approximately $420,630.49.
a. The balance in the fund at the end of the 23-year period, considering a monthly deposit of $1,150 and an annual interest rate of 3.25% compounded annually, is approximately $449,069.51.
To calculate the balance, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where A is the accumulated balance, P is the monthly deposit, r is the annual interest rate, n is the number of compounding periods per year, and t is the number of years.
In this case, we have monthly deposits, so we need to convert the annual interest rate to a monthly rate:
Monthly interest rate = (1 + 0.0325)^(1/12) - 1 = 0.002683
Using this monthly interest rate, we can calculate the accumulated balance over the 23-year period:
A = 1150 * [(1 + 0.002683)^(12*23) - 1] / 0.002683 = $449,069.51
Therefore, the balance in the fund at the end of the 23-year period is approximately $449,069.51.
b. The amount of interest earned over the 23-year period can be calculated by subtracting the total deposits from the accumulated balance:
Interest earned = (Monthly deposit * Number of months * Number of years) - Accumulated balance
Interest earned = (1150 * 12 * 23) - 449069.51 = $420,630.49
Therefore, the amount of interest earned over the 23-year period is approximately $420,630.49.
To learn more about annual interest rate click here: brainly.com/question/20631001
#SPJ11
what is the equation for the idealized regression line? label each part of the equation. what is the equation for the least-squares regression line? label each part of the equation. what are the four assumptions and conditions that must be met in order to perform inference for regression? explain how to check each one. what three aspects of the scatterplot affect the standard error of the regression slope? what is the formula for the standard error for the slope? what is the formula for the sampling distribution for regression slopes? show and explain formulas. if there is no association between two variables, what should be the value of the slope of the regression line?
Answers
The idealized regression line is y = β₀ + β₁x + ε, and the least-squares regression line is Y = b₀ + b₁x. Four assumptions for regression inference are linearity, independence, homoscedasticity, and normality. The standard error of the regression slope is affected by the spread, sample size, and relationship strength. The formula for the standard error of the slope is SEb₁ = √[ Σ(\(y_i - Y_i\))² / (n-2) ] / √[ Σ(\(x_i\) - X)² ]. If there is no association between two variables, the slope of the regression line should be zero.
There are two equations commonly used in regression analysis: the idealized regression line and the least-squares regression line.
The equation for the idealized regression line is
y = β₀ + β₁x + ε
where
y is the dependent variable
x is the independent variable
β₀ is the intercept
β₁ is the slope
ε is the error term
The equation for the least-squares regression line is
Y = b₀ + b₁x
where
Y is the predicted value of y
x is the independent variable
b₀ is the intercept
b₁ is the slope
There are four assumptions and conditions that must be met in order to perform inference for regression
The relationship between the independent variable and dependent variables is called Linearity . To check linearity, plot the dependent variable against the independent variable and look for a straight-line pattern.
Independence, The observations are independent of each other. To check independence, ensure that there is no relationship between the residuals (the difference between the observed value and the predicted value) and any other variables.
The constant variance of errors across independent variable of all level is called homoscedasticity. To check homoscedasticity, plot the residuals against the predicted values and look for a consistent spread of points around zero.
Normality, The errors are normally distributed. To check normality, plot a histogram of the residuals and look for a roughly bell-shaped distribution.
The formula for the standard error for the slope is
SEb₁ = √[ Σ(\(y_i\)- \(Y_i\))² / (n-2) ] / √[ Σ(\(x_i\) - X)² ]
where
\(y_i\), observed value of variable which is dependent for the ith observation
\(Y_i\) is the predicted value of the dependent variable for the ith observation
\(x_i\), the observed value of variable which is independent for the ith observation
X is the mean of the independent variable
n is the sample size
The formula for the sampling distribution for regression slopes is
b₁ ~ N(β₁, σ² / Σ(\(x_i\) - X)²)
where
b₁, least-squares regression line's slope
β₁ is the true population slope
σ² is the variance of the errors
If there is no association between two variables, the slope of the regression line should be zero. it depicts that the variable which is independent has no effect on the variable which is dependent.
To know more about regression line:
https://brainly.com/question/7656407
#SPJ4
simplify the expression if ‖v‖= 2 and ‖u‖= 7. and u . v = 3 (give your answer as a whole or exact number.) (68 = 7v) . v =
Answers
The expression (68 = 7v) . v can be simplified as follows:
(68 = 7v) . v = 68v = 7v^2
The expression ‖v‖= 2 represents the magnitude or length of vector v, which is equal to 2. Similarly, ‖u‖= 7 represents the magnitude or length of vector u, which is equal to 7. Given that u . v = 3, we need to simplify the expression (68 = 7v) . v.
To simplify the expression (68 = 7v) . v, we use the distributive property of dot product. According to the properties of the dot product, we can distribute the scalar value (68 = 7v) to both components of vector v.
Multiplying the scalar value 68 with vector v gives us 68v. Furthermore, since v . v represents the dot product of vector v with itself, it can be written as v^2.
Therefore, the simplified expression is 68v = 7v^2, which represents the result of distributing the scalar value and simplifying the dot product expression.
To learn more about expression refer here:
https://brainly.com/question/28170201#
#SPJ11
Can someone pls help ASAP

Answers
Answer:
89.44
Step-by-step explanation:
using the Pythagorean Theorem: \(a^{2} +b^{2}=c^{2}\)
\(80^{2} +b^{2} =120^{2} \\6400+b^{2} =14400\\b^{2} = 8000\\b = 40\sqrt{5}\)
120 is the hypotenuse so it would be c in the equation.
To solve, I simplified and isolated the variable. I got the square root of 8000 simplified (but idk how to write that out lol)
This answer is closest to 89.44
*Hope this helped! Have a great day/ night wherever you are! : )*
Reflect the triangle over the y-axis and find the coordinate of the image of point K.
K’(2, 1)
K’(–2, 1)
K’(–2, –1)
K’(2, –1)
Answers
K'(-2, 1) is the coordinate of the image of point K, found by multiplying the original x-coordinate of the point K (2) by -1. To reflect the triangle over the y-axis, the x-coordinate of each point is multiplied by -1.
What is triangle?Triangle is a three-sided geometric shape which has three angles and three sides. The three sides of a triangle are typically referred to as the base, the height, and the hypotenuse. A triangle can be classified as either right, obtuse, or acute depending on the measure of its angles. Right triangles have one right angle, obtuse triangles have one obtuse angle, and acute triangles have three acute angles.
The coordinate of the image of point K is K’(-2, 1). This means that the x-coordinate of the point is -2 and the y-coordinate of the point is 1. This can be found by multiplying the original x-coordinate of the point K (2) by -1. The y-coordinate of point K remains the same, so the y-coordinate of the image of point K is 1.
Therefore, the coordinate of the image of point K is K’(-2, 1).
To know more about triangle click-
brainly.com/question/17335144
#SPJ1
What’s the side length?

Answers
Answer:
11.18
Step-by-step explanation:
Pythagorean Theorem:
a² + b² = c²
The hypotenuse is c.
10² + b² = 15²
Square 10 = 100
Square 15 = 225
100 + b² = 225
225 - 100 = 125
Find the Square Root of 125.
11.18033989 or 11.18
Suppose that you are headed toward a plateau 60 m high. If the angle of elevation to the top of the plateau is 20°, how far are you from the base of the plateau?
The plateau ismeters away
(Do not round until the final answer. Then round to two decimal places as needed)
PLEASEEE HELP 83 POINTS TO WHOEVER GET IT RIGHT!!!
Answers
Answer:
164.85 m
Step-by-step explanation:
You have a right triangle with 60 as the side opposite the 20° angle and you are looking for the adjacent side to that angle.
The trig function to use is the tangent of an angle = opp/adj
Let x = distance from you to the base of plateau
So, tan 20 = 60/x
x tan 20 = 60
x = 60/tan 20
x = 164.85 m
You must memorize the definitions all of the trig functions so you can do a problem like this one. OK?
based on a sample of size 41, a 95% confidence interval for the mean score of all students, μ, on an aptitude test is from 60 to 66. find the margin of error.
Answers
To find the margin of error we have to use the formula,
Margin of error = Z * ơ / √n ,
Where
z = critical factor
ơ = population standard deviation
n = sample size
Now we have to find confidence interval
Confidence interval can be defined as a range of values so defined that there is a specified probability that the value of a parameter lies within it.
The confidence interval of a statistical data can be written as.
x+/-zr/√n
x+/-ME
Where margin of error ME = zr/√n
Given that;
Mean = ц
Standard deviation r = 25
Number of samples n = 41
Confidence interval = 95%
z(at 95% confidence) = 1.96
Xbar = 60.............(1)
Xbar + E = 66.........(2)
from equating both the equations we get
E= 6
and for finding the value of margin of error we know that its the half of the E
Margin of error = E/2
=6/2
=3
Therefore , the Margin of error is 3
To know more about the margin of error
https://brainly.com/question/16835723
#SPJ4
The arae (in square cenitmeters) of a square thatnk you card can be represented by x^2+6x+9. What is the permeter of the card when x=4
Answers
The perimeter of the card is 32 centimeters. Perimeter of a square is given by 4x, where x is the length of each side of the square.
Perimeter of a square is given by 4x, where x is the length of each side of the square.
In this case, x=4.
Therefore, the perimeter of the card is 4x = 4(4) = 32.
The perimeter of a square is determined by multiplying the length of each side by 4. In this case, the length of each side of the square tank you card is x=4. Therefore, the perimeter of the card can be calculated by multiplying 4 with 4 which is equal to 32 centimeters. This means that the perimeter of the tank you card when x=4 is 32 centimeters.
Perimeter of a square is given by 4x, where x is the length of each side of the square.
Learn more about square here
https://brainly.com/question/29192128
#SPJ4
create a video explaning the solution of this problem.
help me create a script and the answer for the problem thank you!

Answers
The grounded ends of the guy wires are 15 meters apart.
How to calculate tie valueUsing the Pythagorean theorem, we can calculate the length of the base (distance between the grounded ends of the guy wires).
Let's denote the length of the base as 'x.'
According to the problem, the height of the tower is 20 meters, and the length of each guy wire is 25 meters. Thus, we have a right triangle where the vertical leg is 20 meters and the hypotenuse is 25 meters.
Applying the Pythagorean theorem:
x² + 20² = 25²
x² + 400 = 625
x² = 225
x = √225
x = 15
Therefore, the grounded ends of the guy wires are 15 meters apart.
Learn more about Pythagorean theorem on
https://brainly.com/question/343682
#SPJ1
will give brainliest no files will report Select the correct answer from each drop-down menu.



Answers
Your answer is the center image.
hope this helps.