a high school offers these statistics: 25% of incoming students come from single-parent homes. 75% of incoming students come from two parent homes. 42% of incoming students from single parent homes eventually go on to get a college education.58% of incoming students from two parent homes eventually go on to get a college education. what percent of incoming students eventually go on to get a college education? group of answer choices
Answers
Whereas students from single parent or two parent homes make up 54% of new students, these students eventually go on to complete their college studies..
what is percentage ?By dividing the value by the entire value and multiplying the result by 100, one can compute the percentage. The formula for calculating percentage is (value/total value)100%.When a piece of a whole is stated as a percentage, it is not a fraction but rather a number between 0 and 100. There are three percentages: 100% for everything, 50% for half of it, and 0% for the remaining portion.
calculation
25% of new students come from one-parent households, which equals 0.25;
75% of new students come from two-parent households, which is 0.75.
42% of incoming students from homes with only one parent go on to complete their college studies = 0. 42
58 percent of incoming students who come from two-parent households go on to complete their education =0.58
= 0.25 * 0.42 + 0.75 * 0.58 = 0.54 = 54%.
Whereas students from single parent or two parent homes make up 54% of new students, these students eventually go on to complete their college studies..
To know more about percentage visit :-
https://brainly.com/question/29306119
#SPJ4
Related Questions
Evaluate the integral ∫2ln(x)xdx Select one: a. ln(x)x 2
− 2
x 2
+C b. ln(x)x 2
−x 2
+c c. ln(x)x 2
+ 2
x 2
+C d. ln(x)x 2
+x 2
+c
Answers
The intergration of ∫2ln(x)xdx is ln(x)x^2 + x^2 + C (Option d)
To evaluate the integral ∫2ln(x)xdx, we can use integration by parts.
Let's assume u = ln(x) and dv = 2x dx. Then, we can find du and v using these differentials,
du = (1/x) dx
v = ∫dv = ∫2x dx = x^2
Using the formula for integration,
∫u dv = uv - ∫v du
we have:
∫2ln(x)xdx = uv - ∫v du
= ln(x) * (x)^2 - ∫(x)^2 * (1/x) dx
= ln(x) * (x)^2 - ∫x dx
= ln(x) * (x)^2 - (1/2) * (x)^2 + C
= x^2 (ln(x) - 1/2) + C
Therefore, the correct answer is d. ln(x)x^2 + x^2 + C.
To learn more about Integration visit:
https://brainly.com/question/30094386
#SPJ11
3. At an exhibition, the ratio of the number of men to the number of women was 10:3. Halfway through the exhibition, 110 men left and the number of men was 5/12 of the total number of people who remained behind. How many women were there at the exhibition?
Answers
Answer:
Step-by-step explanation:
Let's assume the initial number of men at the exhibition is 10x, and the initial number of women is 3x.
After 110 men left, the number of men remaining is 10x - 110.
The total number of people remaining is (10x - 110) + (3x) = 13x - 110.
According to the given information, the number of men remaining (10x - 110) is 5/12 of the total number of people remaining (13x - 110). We can write this as an equation:
10x - 110 = (5/12)(13x - 110)
To solve this equation, we can start by simplifying both sides:
10x - 110 = (65/12)x - (55/6)
To get rid of the fractions, we can multiply both sides of the equation by 12:
12(10x - 110) = 65x - 110(2)
120x - 1320 = 65x - 220
Next, we can bring the x terms to one side and the constant terms to the other side:
120x - 65x = 1320 - 220
55x = 1100
Dividing both sides by 55, we find:
x = 20
Now, we can substitute the value of x back into the initial expressions to find the number of men and women:
Number of men = 10x = 10(20) = 200
Number of women = 3x = 3(20) = 60
Therefore, there were 60 women at the exhibition
Hope this answer your question
Please rate the answer and
mark me ask Brainliest it helps a lot
Weighted Undirected Graph
Your task is to implement a Graph class, where every node is denoted by a string, and every edge has a weight. The class should allow the weight to be int.
The class should offer a reasonably effective suite of operations, including but not limited to:
Adding and removing nodes and edges.
The Code
You are provided with two files:
graph.h: this includes most of the basic definitions you will need. You should define data structures to represent a weighted undirected graph and implement the functions so that they can work correctly. You may add new includes, classes, functions, and/or variables to the class per your need, as long as they do not interfere with the existing definitions. You must NOT change the class name, template, parameters, or return types of functions.
graph.cpp: this includes a main function. You may write some code to test your data structures and function implementations for the class. This file will not be marked so you can do anything you like with it -- just ensure it does not cause any error. When the "run" button is pressed, it will compile and run main.cpp.
graph.h
#include
using namespace std;
template // the template allows the weight of an edge to take any numeric data type (denoted by T).
//Class of node to keep track of Vertex value and weight
class Graph {
public:
/* define your data structure to represent a weighted undirected graph */
Graph(); // the contructor function.
~Graph(); // the destructor function.
size_t num_vertices(); // returns the total number of vertices in the graph.
size_t num_edges(); // returns the total number of edges in the graph.
void add_vertex(const string&); // adds a vertex to the graph -- every vertex uses a string as its unique identifier.
bool contains(const string&); // checks if a vertex is in the graph -- returns true if the graph contains the given vertex; otherwise, returns false.
vector get_vertices(); // returns a vector of all the vertices in the graph.
void add_edge(const string&, const string&, const T&); // adds a weighted edge to the graph -- the two strings represent the incident vertices; the third parameter represents the edge's weight.
bool adjacent(const string&, const string&); // check if there is an edge between the two vertices in the graph -- returns true if the edge exists; otherwise, returns false.
vector> get_edges(); // returns a vector of all the edges in the graph -- each edge is represented by a pair of vertices incident to the edge.
vector get_neighbours(const string&); // returns a vector of all the vertices, each of which is directly connected with the given vertex by an edge.
}
graph.cpp
#include "graph.hpp"
PLEASE START IMPLEMENTING FUNCTIONS HERE
Graph::Graph() {}
Graph::~Graph() {}
size_t Graph::num_vertices() {
}
size_t Graph::num_edges() {
}
void Graph::add_vertex(const string& u) {
}
bool Graph::contains(const string& u) {
}
vector Graph::get_vertices() {
}
void Graph::add_edge(const string& u, const string& v, const T& weight) {
}
bool Graph::adjacent(const string& u, const string& v) {
}
Graph::get_edges() {
}
vector Graph::get_neighbours(const string& u) {
}
int main() {. //For testing
Graph g;
g.add_vertex("A");
g.add_vertex("B");
g.add_vertex("C");
g.add_vertex("D");
g.add_vertex("E");
g.add_vertex("F");
g.add_edge("A", "B", 7);
g.add_edge("A", "C", 2);
g.add_edge("C", "D", 4);
g.add_edge("C", "E", 8);
g.add_edge("B", "E", 10);
g.add_edge("A", "E", 6);
g.add_edge("B", "C", 3);
g.add_edge("B", "F", 5);
g.add_edge("E", "F", 10);
g.remove_edge("B", "C");
g.remove_vertex("F");
cout << "Number of vertices: " << g.num_vertices() << endl; // should be 5
cout << "Number of edges: " << g.num_edges() << endl; // should be 6
cout << "Is vertex A in the graph? " << g.contains("A") << endl; // should be 1 or true
cout << "Is vertex F in the graph? " << g.contains("F") << endl; // should be 0 or false
}
Answers
The given code provides a basic framework for implementing a Graph class that represents a weighted undirected graph. The class is designed to work with any numeric data type for the edge weights.
It supports operations such as adding and removing nodes and edges, checking for the presence of a vertex, retrieving the list of vertices and edges, and finding neighboring vertices.
To implement the Graph class, you would need to define appropriate data structures to represent the graph, such as adjacency lists or matrices. You can also use a combination of maps and vectors to store the vertices, edges, and their weights. The provided functions in the code, such as the constructor, destructor, and various member functions, should be implemented with the appropriate logic to manipulate and retrieve the graph data.
For testing purposes, the main function in the graph.cpp file demonstrates the usage of the Graph class. It creates a graph, adds vertices, adds weighted edges between them, removes an edge, and removes a vertex. Finally, it performs some queries to test the implemented functionality, such as retrieving the number of vertices and edges, checking if specific vertices exist in the graph, and printing the results.
The given code provides a starting point for implementing a Graph class that represents a weighted undirected graph. By implementing the necessary data structures and logic for the member functions, you can create a functional graph data structure that supports various operations on the graph.
To know more about undirected graph, visit
https://brainly.com/question/31734665
#SPJ11
Two side lengths of a triangle are 17 meters and 12 meters long. What is the range of possible lengths for the third side?A)5 < s < 29 B)5 < s < 17 C)12 < s < 17 D)12 < s < 29

Answers
Hadas wants to arrange her cards so that they are exactly the same number of cards on each page. if she can arrange the cards both by 6 and by 15, what is the least amount of cards she can have?
Answers
The least amount of cards Hadas can have is 30 cards.
To find the least number of cards Hadas can have, we need to determine the least common multiple (LCM) of 6 and 15.
The LCM is the smallest multiple that both 6 and 15 divide evenly into.
The prime factorization of 6 is 2 × 3.
The prime factorization of 15 is 3 × 5.
To find the LCM, we take the highest power of each prime factor that appears in either number:
LCM = 2 × 3 × 5 = 30
Therefore, the least amount of cards Hadas can have is 30 cards.
To learn more on LCM click:
https://brainly.com/question/24510622
#SPJ1
Una caja de ahorros ofrece a sus clientes un interés simple del 8% anual por una imposición de 18.000 € durante 5 años. ¿ Cual es el importe de los intereses
generados en ese tiempo €
Answers
Una caja de ahorros ofrece a sus clientes un interés simple del 8% anual por una imposición de 18.000 € durante 5 años. de los Interés es = 7,200 €
Interés = Principal × Tasa de interés × Tiempo
Dado que el principal es de 18.000 €, la tasa de interés es del 8% anual y el tiempo es de 5 años, podemos sustituir estos valores en la fórmula:
Interés = 18,000 € × 0.08 × 5
Interés = 7,200 €
Por lo tanto, el importe de los intereses generados en ese tiempo es de 7.200 €. Esto significa que al finalizar los 5 años, el cliente habrá obtenido 7.200 € adicionales como resultado de la imposición de 18.000 € con una tasa de interés del 8% anual. Es importante tener en cuenta que este cálculo se basa en la suposición de que el interés es simple y no se acumula ni se reinvierte.
For more such questions on intereses
https://brainly.com/question/31608291
#SPJ8
A study of iron deficiency among infants compared samples of infants following different feeding regimens. One group contained breastfed infants, while the infants in another group were fed by a standard baby formula without any iron supplements. The summary results on blood hemoglobin levels at 12 months of age are provided below. Furthermore, assume that both samples are sampled from populations that are reasonably normally distributed. (M.F. Picciano and R.H. Deering?The influence of feeding regimens on iron status during infancy,? American Journal of Clinical Nutrition, 33 (1980), pp. 746-753)
Group n x s
Breast-fed 23 13.3 1.7
Fourmula 19 12.4 1.8
(a) Test the hypothesis that there is a difference in the population means between breast-fed infants and formula-fed infants at α = 0.05. Assume the population variances are unknown but equal.
(b) Construct a 95% confidence interval for the difference in population means between breast-fed infants and formula-fed infants. Assume the population variances are unknown but equal.
(c) Write at least one complete sentence describing how your answers to parts (a) and (b) yield the same conclusion about whether there is a difference in the mean blood hemoglobin levels. Hint: Be sure to use the number 0 when discussing the conclusions.
Answers
A. statistically significant difference in the mean blood hemoglobin levels between breastfed infants and formula-fed infants at α = 0.05.
B. the 95% confidence interval for the difference in population means between breast-fed infants and formula-fed infants is (−0.06, 1.18).
C. Both the hypothesis test and the confidence interval lead to the same conclusion that there is a difference in the mean blood hemoglobin levels between the two feeding regimens.
What is null hypothesis?
In statistics, the null hypothesis (H0) is a statement that assumes that there is no significant difference between two or more groups, samples, or populations.
(a) To test the hypothesis that there is a difference in the population means between breast-fed infants and formula-fed infants, we can use a two-sample t-test with equal variances. The null hypothesis is that the population means are equal, and the alternative hypothesis is that they are not equal. Using α = 0.05 as the significance level, the critical value for a two-tailed test with 40 degrees of freedom is ±2.021.
The test statistic can be calculated as:
t = (x1 - x2) / (Sp * √(1/n1 + 1/n2))
where x1 and x2 are the sample means, Sp is the pooled standard deviation, and n1 and n2 are the sample sizes. The pooled standard deviation can be calculated as:
Sp = √(((n1 - 1) * s1² + (n2 - 1) * s2²) / (n1 + n2 - 2))
where s1 and s2 are the sample standard deviations.
Plugging in the values from the table, we get:
t = (13.3 - 12.4) / (1.776 * √(1/23 + 1/19)) = 2.21
Since the absolute value of the test statistic is greater than the critical value, we reject the null hypothesis and conclude that there is a statistically significant difference in the mean blood hemoglobin levels between breastfed infants and formula-fed infants at α = 0.05.
(b) To construct a 95% confidence interval for the difference in population means between breast-fed infants and formula-fed infants, we can use the formula:
(x1 - x2) ± tα/2,Sp * √(1/n1 + 1/n2)
where tα/2,Sp is the critical value of the t-distribution with (n1 + n2 - 2) degrees of freedom and α/2 as the significance level.
Plugging in the values from the table, we get:
(x1 - x2) ± tα/2,Sp * √(1/n1 + 1/n2)
= (13.3 - 12.4) ± 2.021 * 1.776 * √(1/23 + 1/19)
= 0.56 ± 0.62
Therefore, the 95% confidence interval for the difference in population means between breast-fed infants and formula-fed infants is (−0.06, 1.18).
(c) The hypothesis test and the confidence interval both lead to the conclusion that there is a difference in the mean blood hemoglobin levels between breast-fed infants and formula-fed infants. In part (a), we rejected the null hypothesis that the population means are equal, which means we concluded that there is a difference. In part (b), the confidence interval does not contain 0, which means we can reject the null hypothesis that the difference in means is 0 at the 95% confidence level.
Therefore, both the hypothesis test and the confidence interval lead to the same conclusion that there is a difference in the mean blood hemoglobin levels between the two feeding regimens.
To learn more about null hypothesis from the given link:
brainly.com/question/28920252
#SPJ4
Each hour hanna is able to run 4 kilometers. If she has already run 2 kilometers, what will her total distance be after 8 hours?
Answers
Answer:
34km
Step-by-step explanation:
Answer:
I'm assuming that it is asking what her total distance will be after 8 MORE hours?
h=hours
d=total distance
d=4h+2
if h is 8,
d=4(8)+2
d=32+2
d=34
Need answers ASAP!!! Will give brainliest

Answers
Answer:
a. AD and DAB are not congruent
b. point E is 1.5 from point B
c. Yes, your friend is correct
Step-by-step explanation:
(a) tan(C) = opp/adj = 3/4 so C is 36.87 or roughly 37 degrees
so A = 90 - 37 = 53
tan(DAB) = opp/adj = (4/2)/3 = 2/3 so DAB is 33.7 or roughly 34 degrees
so CAD = 53 - 34 = 19
so CAD and DAB are not congruent
(b) angle bisector is the line or line segment that divides the angle into two equal parts. It intersects BC at E so CAE = EAB = 53/2 = 26.5
so tan(26.5) = BE/3
=> BE = 3 x tan(26.5) = 3(0.499) = 1.497 or roughly 1.5
(c) a line from E perpendicular to AC will intersect AC at F, which create angle EFA or EFC a 90 degree angle
Now we have 2 right triangles AEB and AEF with the same hypotenuse which is AE and the same angles at EAF and EAB which means EB and EF are congruent
a basket contains 5 purple pencils and 9 brown pencils. if two pencils are picked at random one after the other with replacement, then what is the probability that both the pencils are purple?
Answers
The probability that both pencils picked at random with replacement from a basket containing 5 purple and 9 brown pencils are purple is 9/98.
To calculate the probability of picking two purple pencils with replacement, we need to use the multiplication rule of probability. The probability of picking the first purple pencil is 5/14, and the probability of picking a second purple pencil from the basket is also 5/14 since we are replacing the first pencil. Therefore, the probability of picking two purple pencils with replacement is (5/14) × (5/14) = 25/196. However, we also need to account for the possibility of picking a brown pencil first and a purple pencil second.
The probability of picking a brown pencil first is 9/14, and the probability of picking a purple pencil second is 5/14. So, the probability of picking a brown pencil followed by a purple pencil is (9/14) × (5/14) = 45/196. Adding the probability of picking two purple pencils and the probability of picking a brown pencil followed by a purple pencil gives us the total probability of (25/196) + (45/196) = 9/98.
Therefore, the probability that both pencils picked at random with replacement from a basket containing 5 purple and 9 brown pencils are purple is 9/98.
To learn more about probability here:
brainly.com/question/30034780#
#SPJ11
Find the area of a regular
polygon with 5 sides that has a
side length of 6 inches and an
apothem of 9 inches.
Answers
Answer:
Step-by-step explanation:
Height of the triangle = apothem = 9 inches
Base = 6 inches
\(Area \ of \ triangle = \frac{1}{2}bh\\\\=\frac{1}{2}*6*9\\\\= 3*9\\\\= 27 \ in^{2}\)
Area of regular polygon = Area of 5 triangle.
= 5 * 27
= 135 square inches

answer this question.

Answers
Using the sine function with the given angle C and hypotenuse, we find that the length of the side x is approximately 16.23 units.
We can use the trigonometric ratios of the right triangle to find the length of the side x. Since we know the angle C and the hypotenuse, we can use the sine function, which relates the opposite side to the hypotenuse
sin(C) = opposite / hypotenuse
sin(37°) = x / 27
Multiplying both sides by 27, we get
x = 27 sin(37°)
Using a calculator, we find that
x ≈ 16.23
Therefore, the length of the side x is approximately 16.23 units.
To know more about sine function:
https://brainly.com/question/12015707
#SPJ1
f(x) = x² + 6x-2, g(x) = x-6, find f(g(4)) and (gof)(-4).
Answers
Answer:
f(g(4)) = -10
(g o f)(-4) = -16
Step-by-step explanation:
Function composition is an operation where one or more functions are substituted into another function.
Given functions:
\(\begin{cases}f(x)=x^2+6x-2\\g(x)=x-6\end{cases}\)
The given composite function f(g(4)) means to substitute the function g(4) in place of the x in function f(x). The function g(4) is the value of function g(x) when x = 4.
\(\begin{aligned}f\left(g(4)\right)&=\left(g(4)\right)^2+6\left(g(4)\right)-2\\&=\left(4-6\right)^2+6\left(4-6\right)-2\\&=\left(-2\right)^2+6\left(-2\right)-2\\&=4-12-2\\&=-8-2\\&=-10\end{aligned}\)
The given composite function (g o f)(-4) means to substitute the function f(x) in place of the x in function g(x), then substitute x = -4 into the resulting function.
\(\begin{aligned}\left(g \circ f \right)(-4)&=g\left(f(-4)\right)\\&=\left(f(-4)\right)-6\\&=((-4)^2+6(-4)-2)-6\\&=(16-24-2)-6\\&=-10-6\\&=-16\end{aligned}\)
x-9/2=-12 guys please help
Answers
Step-by-step explanation:
How to solve for x?
Eliminate -(9/2) to find out the value of x.
Add 9/2 to both sides of the equation:
\(x = - 7.5\)
Answer
\(x=\) \(-7.5\)
Step-by-step explanation:
\(x -\frac{9}{2} = -12\)
\(x -\frac{9}{2} + \frac{9}{2} = -12 + \frac{9}{2}\) (add \(\frac{9}{2}\) to both sides)
\(x = -\frac{15}{2}\)
\(-\frac{15}{2} =\) \(-7.5\)
\(x=\) \(-7.5\)
What is the name for a company that is taxed on the individual tax forms of its owners, and never as a separate
independent entity?
A A double taxation company
B. A tax exempt corporation
C. A nonprofit corporation
D A pass-through entity
Answers
Can someone help me with this please and thanks :)

Answers
What is the solution set for 4x - (x + 1) < 5x - 7 ?
A. x < -6
B. x < -8
C. x > 4
D. x > 3
Answers
4x - (x + 1) < 5x - 7
4x - x - 1) < 5x - 7
3x - 5x < -7 + 1
-2x < -6
2x > 6
x > 3
Given that 1 kilometer = 0.62 mile, 36 inches = 1 yard, and 1 mile = 1760 yards, approximately how many inches are in 1 km?
Answers
Given that 1 kilometer = 0.62 mile, 36 inches = 1 yard, and 1 mile = 1760 yards, 1 km has approximately 39,283.2 inches.
In mathematics, conversion is the process of changing the value of one form or unit to another. It can be changing ones unit of length, weight, volume or even currency to another.
A conversion factor is a number used to change one set of units to another, either by multiplying or dividing.
From the problem, the conversion factors are given as
1 kilometer = 0.62 mile
36 inches = 1 yard
1 mile = 1760 yards
To convert 1 kilometer into inches, first, convert 1 kilometer to miles using the conversion factor, 1 kilometer = 0.62 mile
1 km = 0.62 miles
Then, convert miles to yards using the conversion factor, 1 mile = 1760 yards
1 km = 0.62 miles = 0.62 (1760 yards)
1 km = 0.62 miles = 1091.2 yards
Lastly, convert yards to inches using the conversion factor, 36 inches = 1 yard
1 km = 0.62 miles = 1091.2 yards = 1091.2 (36 inches)
1 km = 0.62 miles = 1091.2 yards = 39,283.2 inches
To learn more about conversion: https://brainly.com/question/97386
#SPJ4
1/3x+6=-18+3x PLEASE HURRY I HAVE A TEST
Answers
Answer:
x=9 Hope this helps :)
Step-by-step explanation:
Step 1: Simplify both sides of the equation.
Step 2: Subtract 3x from both sides.
Step 3: Subtract 6 from both sides.
Step 4: Multiply both sides by 3/(-8).
And you get x=9
What is the mass of Cl2
Answers
Answer:
molar mass of carbon-12
Step-by-step explanation:
At the end of a 5-year term, what is the balance of an $8,000 investment at a simple interest rate of 1. 8 percent?
Round to the nearest dollar.
$8,000
$8,720
$8,751
$9,382
PLEASE HELP ASAP!!!!!!!!!!!!!!! QUESTION 47 CONCUMER MATH
Answers
Answer:
$8,720
Step-by-step explanation:
SI = PRT where;
SI = simple interest
P = principal amount/starting amount
R = rate as a decimal/fraction
T = time in years
I = 8000 . 5 . 0.018
I = 720
8000 + 720 = 8720
Malik buys and sells car parts. He bought two tires for $45.00 each and later sold them for $65.00 each. He bought three rims for $85.00 each and later sold them for $126.00 each. He bought five headlight covers for $5.00 each and later sold them for $15.00 each. What is Malik's total profit?

Answers
Answer: $75
Step-by-step explanation: First he bought tires for 45.00 dollars - later sold it as 65.0 dollars.
=> 65 - 45 = 20 dollars is his profit
he brought 3 rims for 85 dollar - then later sold it as 126 dollars
=> 126 - 85 = 41 dollars
He bought headlight for 5.00 dollars then sold it later for 15 dollars.
=> 15 - 5 = 10 dollars
Total expenses
=> 134
Total amount sold
=> 209
Profit => 209 - 134 = 75 dollars
Mila used the multiplication property to justify the first step in solving an equation. The original equation was x/2+4=10. What could the equation have been transformed into after this step
Answers
Answer: \(x+8=20\)
Step-by-step explanation:
Given
Equation is \(\frac{x}{2}+4=10\)
Mila uses the first step as multiplication to make the coefficient of x, 1
Mila maybe have multiplied the whole equation by 2 i.e.
\(\Rightarrow 2\left(\dfrac{x}{2}+4=10\right)\\\\\Rightarrow x+8=20\)
a square piece of land take 24ft. of fence to surround it how much square ft is the area of the 24 ft land..
Answers
The Solution:
Given:
The perimeter of the square piece of land is 24 ft.
We are required to find the area of the given piece of land.
Step 1:
By formula,
\(\begin{gathered} P=4l \\ where \\ P=perimeter=24ft \\ l=length=? \end{gathered}\)So,
\(\begin{gathered} 4l=24 \\ \\ l=\frac{24}{4}=6ft \end{gathered}\)Step 2:
Find the area of the piece of land.
\(\begin{gathered} A=l^2 \\ where \\ A=area=? \\ l=6\text{ ft} \end{gathered}\)\(A=6^2=36ft^2\)Therefore, the correct answer is 36 square feet.
Rewrite the equation 8x + 6x2 - 7= in standard form and identify a, b, and c.
Select one:
a. a =5,b= 8.c = -7
b.a=6,6= 8,0 = 1
ca=5,b=8,0= 7
da= 8,b= 6.c = -7
40
Answers
Answer:
a = 6
b = 8
c = -7
Step-by-step explanation:
In standard form, we have ;
y = ax^2 + bx + c
Here, we have;
6x^2 + 8x - 7
a is the coefficient of x^2 which is 6 in this case
b is the coefficient of x which is 8
c is the last number which is -7
So we have;
a = 6
b = 8
c = -7
Which value, when placed in the box, would result in a system of equations with infinitely many solutions? y = -2x + 4 6x + 3y = -12 -4 4 12
Answers
Answer:
Option (4)
Step-by-step explanation:
The given system of equations is,
y = -2x + 4 ------ (1)
6x + 3y = a --------(2)
We have to find the value of a for which the system of equations will have infinitely many solutions.
Option (1). If a = -12
6x + 3y = -12
2x + y = -4
y = -2x - 4
Both the equations have same slope, therefore, they are parallel and will have no solutions.
Option (2). If a = -4
6x + 3y = -4
3y = -6x - 4
\(y=-2x-\frac{4}{3}\)
Then equation (1) and (2) will intersect each other at least at one point Or there is exactly one solution of the system of the equations.
Option (3). If a = 4
6x + 3y = 4
3y = -6x + 4
y = -2x + \(\frac{4}{3}\)
Then equation (1) and (2) will intersect each other at least at one point Or there is exactly one solution of the system of the equations.
Option (4). If a = 12
6x + 3y = 12
3y = -6x + 12
y = -2x + 4
Therefore, both the equations (1) and (2) are same for a = 12 and they will have infinitely many solutions.
This question is based on system of linear equation .Thus, for a=12 will have infinitely many solution.
Given:
y = -2x + 4 ------ (a)
6x + 3y = a ------(b)
We need to determined the value of a for which the system gives infinitely many solution.
Now check all the options as given below:
Option(1) a = -12 and put it in (b) we get,
6x + 3y = -12
2x + y = -4
y = -2x - 4
Both the equations have same slope, therefore, they are parallel to each other and have no solutions.
Option(2) a= -4 and put it in (b) we get,
6x + 3y = -4
3y = -6x - 4
\(y=-2x-\dfrac{4}{3}\)
Therefore, the equation has unique solution. Thus, both lines intersect each other at one point and there is unique value of x and y.
Option(3) a= 4
6x + 3y = 4
3y = -6x + 4
\(y=-2x+\dfrac{4}{3}\)
Therefore, the equation has unique solution. Thus, both lines intersect each other at one point and there is unique value of x and y.
Option(4) a= 12
6x + 3y = 12
3y = -6x + 12
y = -2x + 4
Both the equation are same for a= 12.
Thus, for a=12 will have infinitely many solution.
For further details, please prefer this link:
https://brainly.com/question/13712241
Solve the equation 4a – (6 – 5a) + 12 = 3a + 2(2a – 4) for a.
Could you help me?
There are no options for this answer. It must be solved
Answers
Answer:
a = -7
Step-by-step explanation:
4a – (6 – 5a) + 12 = 3a + 2(2a – 4)




Please help, tysm :)

Answers
Answer:
Step-by-step explanation:
the second one
HK and IJ
Answer:
Its the last one DH and FG
URGENT HELP!!
The angle between a diagonal and the longer base of the isosceles trapezoid MNFD is 45°. NK is an altitude to the longer base. If MD = 9 and NF = 5, find:
Answers
Answer:
NK = 7, MK = 2, MF = 9.9, Area = 42Step-by-step explanation:
Refer to attached
To find:
NK , MK, MF, Area of trapezoidSolution
The trapezoid is isosceles and NK is its height, therefore
MD - NF = 2MKMK = (9 -5)/2 = 2Since ∠KDN = 45°, the triangle NKD is isosceles and so
NK = KD = MD - MK = 9 - 2 = 7MF = ND as trapezoid is isosceles and therefore diagonals are equal
ND = NK√2 = 7√2 = 9.9 So MF = 9.9Area of trapezoid
A = 1/2(b1 + b2)h A = 1/2(9+5)(7) = 6*7 = 42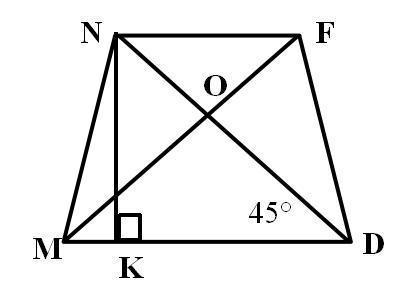
nth term of a sequence is n(n+1) what term is 240? is 55 a term in the sequence?
Answers
Answer:
a₁₅ = 240 55 is not term in the sequenceStep-by-step explanation:
\(n(n+1)=240\\\\n^2+n-240=0\\\\n=\dfrac{-1\pm\sqrt{1-4(-240)}}{2}=\dfrac{-1\pm\sqrt{1+960}}{2}=\dfrac{-1\pm31}{2}\quad\wedge\quad n\in N_+\\\\n=15\)
if n is even number then (n+1) is odd number and if n is odd number then (n+1) is even number
The product of numbers where one of them is even will always be even.
55 is odd number so it is not term of this sequence.