A helicopter flies 665 feet above ground. What is the measure of the angle of depression from the helicopter to the girl’s line of sight? Round to the nearest degree. 23° 25° 65° 67°
Answers
Answer:
67°
Step-by-step explanation:
Given:
Height of helicopter from the ground, x = 665 feet
Distance from the helicopter to the girl's line of sight(opposite) = 665ft - 5 ft = 600 ft
Horizontal distance(adjacent) = 280 ft
To find the angle of depression, use the formula:
\( tan y = \frac{x}{y} \)
Solve for y:
\(y = tan^-^1 (\frac{x}{y})\)
\(y = tan^-^1 (\frac{660}{280}) = 67.01\)
Angle of depression = 67°

Answer:
67 degrees
Step-by-step explanation:
Related Questions
Jacob has several babysitting jobs.on one job ,he earned $10 an hour plus an extra $20 since there were 3 children.On another job , he earned $15 an hour.He earned the same amount of money at both jobs .how many hours did he work and how much did he earned?
Answers
Jacob worked for 1 hour in his first job and 2 hours in his second job. Jacob earned $30 in both jobs.
Let's suppose that Jacob worked for x hours in his first job.
According to the statement, he earned $10 per hour.
Also, he earned an extra $20 since there were 3 children.
Therefore, the total amount he earned in his first job can be calculated as $10x + $20.
Now let's suppose that Jacob worked for y hours in his second job.
According to the statement, he earned $15 per hour.
Therefore, the total amount he earned in his second job can be calculated as $15y.
It is given that Jacob earned the same amount of money in both jobs.
Therefore, we can set up the equation as: $10x + $20 = $15y
Simplifying the above equation:
10x + 20 = 15y10x = 15y - 20 (subtracting 20 from both sides)
2x = 3y - 4 (dividing both sides by 5)
Now we know that x and y are integers.
Therefore, 3y - 4 must be a multiple of 2.
The smallest such number is 2.
Therefore, we can set up the equation as:
3y - 4 = 2
Now solving the above equation:
3y = 6y = 2Since y = 2,
we can now find x as follows:
2x = 3y - 42x = 3(2) - 42x = 6 - 4x = 1
Therefore, Jacob worked for 1 hour in his first job and 2 hours in his second job.
Now, we can calculate the total amount he earned as:
$10(1) + $20 = $30$15(2) = $30
Therefore, Jacob earned $30 in both jobs.
To know more about hour visit:
https://brainly.com/question/13349617
#SPJ11
Find the exact value by using a half angle identity.tan 75°
Answers
The trigonometric function is given as
\(\tan 75^{\circ}\)Apply the half angle identity to find the value of tan 75 ,
\(\tan (\frac{u}{2})=\frac{\sin u}{1+\cos u}\)Here,
\(\tan (\frac{150^{\circ}}{2})=\frac{\sin150^{\circ}}{1+cos150^{\circ}}\)\(\tan (75^{\circ})=\frac{\frac{1}{2}}{1-\frac{\sqrt[]{3}}{2}}=\frac{\frac{1}{2}}{\frac{2-\sqrt[]{3}}{2}}^{}\)\(\tan 75^{\circ}=\frac{1}{2-\sqrt[]{3}}\)Now rationalize the function.
\(\tan 75^{\circ}=\frac{1}{2-\sqrt[]{3}}\times\frac{2+\sqrt[]{3}}{2+\sqrt[]{3}}=\frac{2+\sqrt[]{3}}{4-3}=\frac{2+\sqrt[]{3}}{1}\)Again simplify the trigonometric function,
\(\tan 75^{\circ}=2+1.732=3.732\)Hence the answer is 3.732.
Suppose Q is the midpoint of PR. PR = 9x - 31 and QR = 43. Find X
Answers
Greetings from Brasil...
Since Q is the central point of PR, then PQ = QR and PQ = PR/2 or QR = PR/2
QR = PR/2
PR = 2 · QR
9X - 31 = 2 · 43
X = 13
The value of x is 13.
What is a line segment ?A line segment is basically a line which has two end points.
A line has always a linear equation which has highest degree of 1
According the given question
Line segment is PR and midpoint is Q
Given QR = 43 which one end to the midpoint
∴ Total length of the line segment is 2×43
= 86
Given PR = 9x - 31 which is the total length of the line segment.
∴ 9x - 31 = 86
9x = 86 + 31
9x = 117
x = 117/9
x = 13.
Learn more about line segment here :
https://brainly.com/question/25727583
#SPJ6
Using your knowledge of prime factorisation, find “m” if 3x m3 = 375
(Show sufficient workings)
Answers
Answer:
is 300 trust me
Step-by-step explanation:
compare the slopes and y intercepts of the graphs of the equations in the linear system 8x + 4y =12 and 3y = -6x -15 to determine whether the system has one solution no solutions or infinitely many solutions explain
Answers
Answer:
No solutions
Step-by-step explanation:
Convert both equations into y = mx + b form, where m is the slope and b is the y intercept.
8x + 4y = 12
4y = -8x + 12
y = -2x + 3
Rearrange the other equation:
3y = -6x - 15
y = -2x - 5
So, both equations have a slope of -2. But, one has a y intercept of 3 and the other has a y intercept of -5.
Because the lines have the same slope but different y intercepts, the lines are parallel.
Parallel lines have no solutions, because they will never intersect.
So, the system has no solutions.
What is the value of this expression:
Square root = 25+144
Answers
Answer:
√28561
Step-by-step explanation:
√ = 169
Square root of 169 = 169²
√28561 = 169
[I apologize if I misunderstood the question.]
cashapp me $AndrewTkacs
Answers
Answer:
sure when i have money
Step-by-step explanation:
i don't have money lol
In triangle TGP, Look at picture if confused by what I asked

Answers
∠T is congruent or equal to triangle TGA.
option D.
What is a right triangle?
A right triangle is a type of triangle that has one angle measuring 90 degrees (a right angle) while the two remaining angles are known as complementary angles because they sum up to 90 degrees.
For the diagram given in this question, we can conclude that angle PAG is 45 degrees and angle TAG is also 45 degrees, since the line AG bisector angle PGT into two.
Angle TAG = 90⁰
angle TGA + angle GTA = 90 (complementary angles)
TGA = 45⁰ ≅ ∠T
Learn more about complementary angles here: https://brainly.com/question/16281260
#SPJ1
What is the equation of the line perpendicular to y=-0.5x-4 and with the same x-intercept as
3x-4y=12?
Answers
Answer:
4dfhhtxghgggytxxgg
Step-by-step explanation:
ez
What is the surface area of the rectangular pyramid below? (assume they are in cm²) Awnser Choices:
A. 320cm²
B. 440 cm²
C. 471 cm²
D. 251.6 cm²
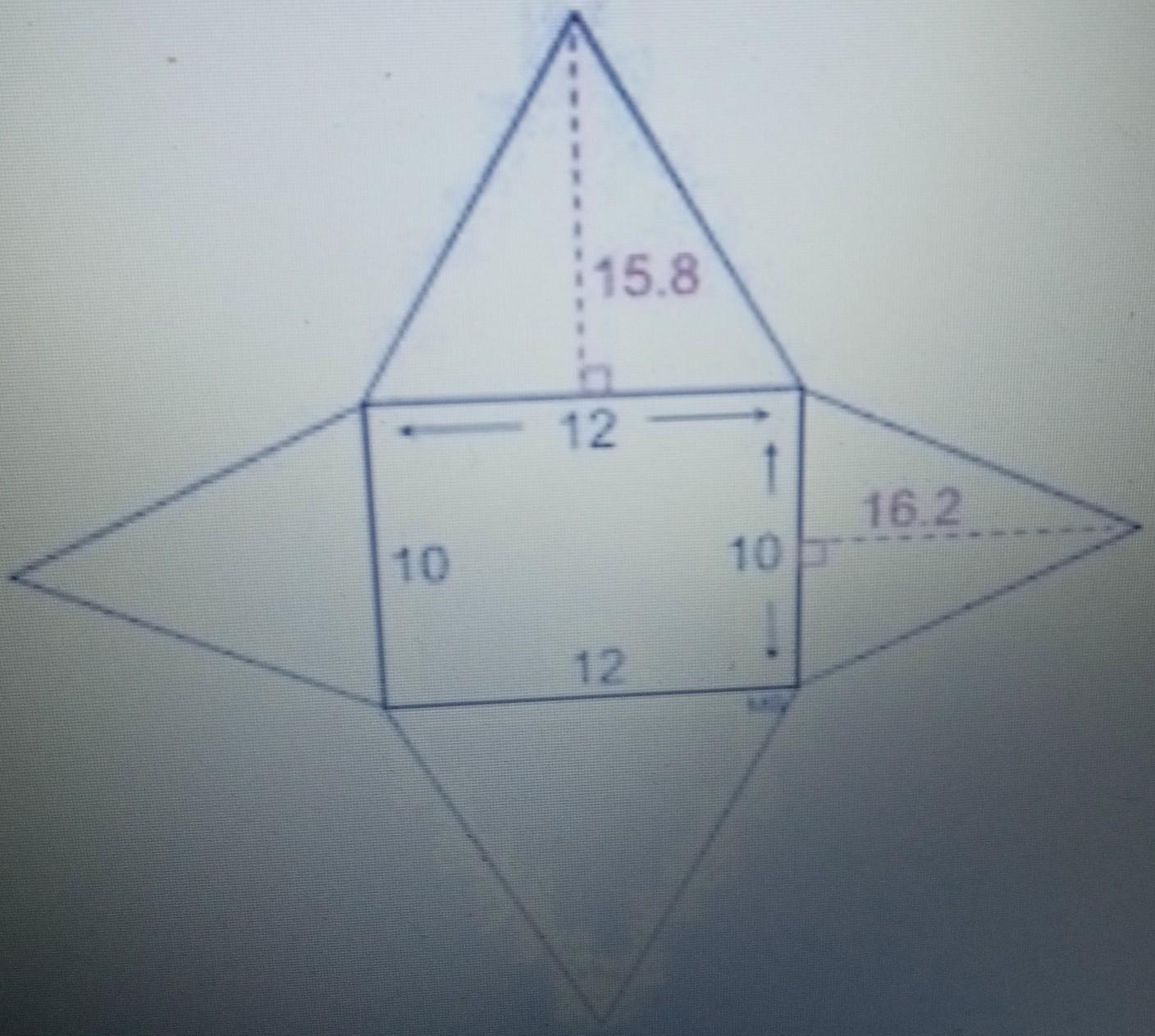
Answers
The Surface area of the rectangular pyramid that is given in the image is: C. 471 cm².
How to Find the Surface Area of a Rectangular Pyramid?The surface area is simply the space covered by the faces of the pyramid . Therefore:
Surface area = area of the rectangular face + the four triangular faces
Note that there are two pairs of identical triangular faces.
Area of the first pair of triangular faces = base * height = 10 * 16.2 = 162 cm²
Area of the second pair of triangular faces = base * height = 12 * 15.8 = 189.6 cm²
Area of the rectangular face = length * width = 12 * 10 = 120 cm².
Surface area of the rectangular pyramid = 120 + 189.6 + 162 = 471.6 cm².
Learn more about rectangular pyramid on:
https://brainly.com/question/27270944
#SPJ1
What can use the distributive property to the algebraic expression 5(x - 7)
Answers
Usibg the distributive property to the algebraic expression 5(x - 7) will be 5x - 35.
What is distributive property?The formula for the distributive property is expressed as, a × (b + c) = (a × b) + (a × c); where, a, b, and c are the operands. Here, the number outside the brackets is multiplied with each term inside the brackets and then the products are added.
When you multiply a value by a sum, the distributive property of multiplication over addition is used. Say you want to multiply 5 by the product of 10 plus 3. When two terms are similar, we typically add the two numbers before multiplying by 5. However, the property states that you should first multiply each addend by 5.
Therefore, 5(x - 7) will be:
= 5(x) - 5(7)
= 5x - 35
Learn more about expressions on:
https://brainly.com/question/723406
#SPJ1
A company constructs a bridge 500 metres long. The cost of constructing the first me- tre is N1000 with an increase in cost of N500 per metre for every succeeding metre. Calculate the total cost.
Answers
Answer:
N 62,875,000
Step-by-step explanation:
Cost of first meter is 1000
Each subsequent meter costs 500 more than the previous meter. So the costs per meter and sum can be expressed as
1st meter cost = 1000
2nd meter cost = 1500
3rd meter cost = 2000
4th meter cost = 2500
.....
Looking at the numbers above we see that they form an arithmetic sequence with 1000 as the first term, a common difference of 500 and with 500 terms
The total cost will the sum of the 500 terms in the series
The sum of an arithmetic sequence with n terms is given by
\(S_n = \dfrac{n}{2}\cdot (2a_1 + (n-1)\cdot d)\)
where
a₁ is the first term
d is the common difference
n is the number of terms
Sₙ is the sum of the first n terms
Substituting a₁=1000, d = 500, n =500 gives us:
\(S_{500} = \dfrac{500}{2}\cdot (2\cdot 1000 + (500-1)\cdot 500)\)
\(S_{500} = 250\cdot (2000 + 499\cdot 500)\\\\S_{500} = 250(2000 + 249500)\\\\\\S_{500} = 250\cdot 252500\\\\\\S_{500} = 250\cdot 251500\\\\S_{500} = 62,875,000\)
Total cost of constructing the bridge is N 62,875,000
Vicky jogged 2 3/4 miles in 1/2 hour. What was her average rate of speed in miles per hour?
Answers
Answer:
5 1/2
Step-by-step explanation:
a) r=d/t
11/4x2/1= 22/4= 5 1/2
b) 1/2 hour x 2 equals one hour, so 2 3/4 x 2 equals rate per hr.
11/4x2=22/4= 5 1/2
Answer:
1 mph
Step-by-step explanation:
All you have to do is follow the formula. Distance/time=mph
Ao and bo are two equal roads meeting at an angle of 60. a and b are joined by a straight road ab and also by a radial road acb. find to the nearest metre by how much the radial road is longer than the straight line
Answers
The radial road is longer than the straight line by approximately 0.154 m. Therefore, the required answer is 0.154 m.
Given: AO = BO, ∠AOB = 60°, and AB is joined by straight road ACB and radial road AB.
To Find: By how much radial road AB is longer than the straight line?
Let's construct the diagram below, In triangle AOB, using the sine rule:
AB / sin ∠ABO = BO / sin ∠BAO, AB / sin 60° = BO / sin 60° => AB = BO ...(i)
Let AC = BC = x m ∴ AB = 2x m (Since ∠AOC = ∠BOC = 60°)
In triangle ABC, using the cosine rule:AB² = AC² + BC² - 2ACBC cos ∠CAB(2x)² = x² + x² - 2(x)(x)(cos 120°)4x² = 2x² + x² + 2(x² )∴ x² = 2x² / 3 => x = (2 / √3)x
Let AD be the perpendicular distance of C from AB.
Then, AD = (x)sin 60° = (x√3 / 2) m And BD = (x)sin 30° = (x / 2) m
Thus, AB = AD + BD = (x√3 / 2) + (x / 2) = (2x + x√3) / 2From eq. (i), we have BO = 2x m
Therefore, radial road ACB is longer than straight line AB by = ACB - AB= (2x + x√3) / 2 - 2x= x(√3 - 2) / 2= [2 / √3]× [√3 - 2]≈ 0.154 m
Learn more about sine:
https://brainly.com/question/30162646
#SPJ11
URGENT!!! which is a true statement about triangle ABC?

Answers
Answer:
1st option
Step-by-step explanation:
In right triangle BCD
cosC = \(\frac{adjacent}{hypotenuse}\) = \(\frac{b-x}{a}\) ( multiply both sides by a )
b - x = acosC ( subtract b from both sides )
- x = acosC - b ( multiply through by - 1 )
x = b - acosC
What is (x + y + 3)(x + y - 4)
Answers
Answer:
x^2+2xy+y^2-x-y-12.
what is (3x – 2)(4x + 1) =
Answers
Answer:
\(12x^{2} -5x -2\)
Step-by-step explanation:
We multiply the first term 3x by 4x and then 3x multiplied by one. We proceed to multiply by -2 by 4x and multiplied by -2 +1. We finally add and get the result.
\(12x^{2} -5x -2\)
Translate: two is four more than a number, x
Answers
2 is 4 more than -2
I know this because there is no positive number -4 from 2 so you need to go to the negatives which means 2, 1 ,0, -1,-2.
Hope this helped<3
Have a wonderful day...
-Dignoris :)
7. The ratio of width to length of the United States flag is 10:19.
If the width of the flag at Emersen's school is 4 feet, what is its length in feet?
Answers
X=4/19
10x=10x4/9
40/19
3.2 and. 4.8 what is the scale factor of dilation
Answers
Answer:
1:1.5
Step-by-step explanation:
Use algebra:
3.2 to 4.8 = 1 to x
\(\frac{3.2}{4.8} = \frac{1}{x}\)
Now cross-multiply:
3.2x=4.8×1
x=\(\frac{4.8}{3.6}\)
x=1.5
(extra credit) suppose you have a well-balanced "super coin" with three sides or outcomes equally likely: head, middle, and tail. (the super coin is a die with opposite faces showing head, middle, and tail) you tossed this super coin two times.
Answers
Possible outcomes are Head, Middle, and Tail.
Since all outcomes are equally likely, the probability of each event is same, therefore
P(Head) = P(Middle) = P(Tail)
= 1/3
P(B|A) is 1/3
P(C|A) is 2/3
A and B are independent
A and C are not independent
Part a
Finding the sample space, S
S = { (HH), (HM), (HT), (MH), (MM), (MT), (TH), (TM), (TT) }
Part b
Finding P(B|A) and P(C|A):
n(B and A) = no. of outcomes in which the first toss is Middle and second toss is Tail = 1
n(A) = Total no. of events in which the first toss is Middle = 3
Therefore, P(B|A) = 1/3
n(C and A) = no. of outcomes in which the first toss is Middle and total no. of heads is zero = 2
n(A) = Total no. of events in which the first toss is Middle = 3
Therefore, P(C|A) = 2/3
Part c
Finding if A and B are independent, or if A and C are independent
Two events A and B are said to be independent when the occurrence of one event does not affect the occurrence of the other event and vice versa. In case of independent events,
P(A) = P(first toss is Middle) = 3/9 =1/3
P(B) = P(second toss is Tail) = 3/9 = 1/3
P(A and B) = P(first toss is Middle and second toss is Tail) = 1/9
P(A)*P(B) = (1/3)*(1/3)
= 1/9 = P(A and B)
Hence, we can say that events A and B are independent.
For A and C, we have,
P(A) = P(first toss is Middle) = 3/9
P(C) = P(total no. of Heads is 0) = 4/9
P(A and C) = P(first toss is Middle and total no. of heads is 0) = 2/9
P(A)*P(C) = (3/9)*(4/9)
= 4/27 P(A and C)
Hence, events A and C are not independent.
The question was incomplete, the complete question is:
(Extra Credit) Suppose you have a well-balanced "super coin" with three sides or outcomes equally likely: Head, Middle, and Tail. (the super coin is a die with opposite faces showing Head, Middle, and Tail) You tossed this super coin two times
a) Describe the sample space using the notation HM for example, if the results are Head first, and Middle second.
Let;
A = event the first toss is Middle,
B = event the second toss is Tail, and
C = event the total number of Heads is 0.
b) Find
P(B|A)
P(C|A)
c) Are A and B independent? YES, NO, Why?
Learn more about probabilities here:
https://brainly.com/question/25163406
#SPJ4
Find the 7th term of the geometric progression which begins -6250, 1250, -250
Answers
Answer:
\(-\frac{2}{5}\)
Step-by-step explanation:
The geometric progression given is:
-6250, 1250, -250...
The first term (a) is -6250, and the common ratio (r) can be gotten by dividing the second term by the first term:
r = 1250/-6250 = \(-\frac{1}{5}\)
A geometric progression is generally given as:
\(a_n = ar^{n - 1}\)
where \(a_n\) = nth term
The 7th term of the progression above is therefore:
\(a_7 = -6250 * (-\frac{1}{5} )^6\\\\a_7 = -\frac{2}{5}\)
The 7th term of the geometric progression is;
a_7 = -2/5
The formula for the nth term of a geometric progression is;
a_n = ar^(n - 1)
Where;
a is first term
r is common ratio
n is the position of the term in the series
We are given the series;
-6250, 1250, -250...
Thus;
First term; a = -6250
Common ratio; r = 1250/-6250
r = -1/5
Thus;
a_7 = -6250(-1/5)^(7 - 1)
a_7 = -2/5
Read more at; https://brainly.com/question/25724889
What is the slope of the line?

Answers
Answer:
Slope = (1/3)
Step-by-step explanation:
Point 1: (0, 2); Point 2: (3, 3)
(x₁, y₁) (x₂, y₂)
y₂ - y₁ 3 - 2 1
m = ----------- = ------------ = ---------
x₂ - x₁ 3 - 0 3
y - y₁ = m(x - x₁)
y - 2 = (1/3)(x - 0)
y - 2 = (1/3)x - 0
+2 +2
--------------------------
y = (1/3)x + 2
I hope this helps!
please give a reasonable answer please and thank you!

Answers
The inequality on the graph is a linear inequality, and it can be written as:
y > 2x - 4
What inequality is shown in the graph?On the graph, we can see a linear inequality, we can see a dashed line with a positive slope, and the shaded area is above that line, so the inequality is of the form:
y > line.
A general linear equation is written as:
y = a*x + b
Where a is the slope and b is the y-intercept.
If the line passes through two points (x1, y1) and (x2, y2), then the slope is:
a = (y2 - y1)/(x2 - x1)
We can find two points on the graph, we can see that the line passes through (0, -4) and (2, 0), then the y-intercept is -4 and the slope is:
a = (0 + 4)/(2 - 0) = 2
y = 2x - 4
then the inequality is:
y > 2x - 4
Learn more about inequalities:
https://brainly.com/question/24372553
#SPJ1
If people are present in a room, what is the probability that no two of them celebrate their birthday on the same day of the year? how large need be so that this probability is less than ?
Answers
The number needed so that this probability is less than 1/2 is 23.
How to illustrate the information?It should be noted that the first person can have any birthday. The second person's birthday has to be different. There are 364 different days to choose from, so the chance that two people have different birthdays is 364/365.
To find the probability that both the second person and the third person will have different birthdays:
(365/365) * (364/365) * (363/365) = 132
132/133 = 99.18%.
If we want to know the probability that four people will all have different birthdays, we multiply again:
(364/365) * (363/365) * (362/365)
= 98.36%.
We can keep on going the same way as long as we want. A formula for the probability that n people have different birthdays is
((365-1)/365) * ((365-2)/365) * ((365-3)/365) * . . . * ((365-n+1)/365).
365! / ((365-n)! * 365^n).
We know that the probability of finding at least two people with the same birthday is 1 minus the probability that everybody has a different birthday. It turns out that the smallest class where the chance of finding two people with the same birthday is more than 50% is... a class of 23 people. The probability is then about 50.73%.
Learn more about probability on:
https://brainly.com/question/24756209
#SPJ4
Complete question
If n people are present in a room, what is the probability that no two of them celebrate their birthday on the same day of the year? how large need be so that this probability is less than 1/2?
Find the center of mass of the wire that lies along the curve r and has density =4(1 sin4tcos4t)
Answers
The mass of the wire is found to be 40π√2 units.
How to find the mass?To calculate the mass of the wire which runs along the curve r ( t ) with the density function δ=5.
The general formula is,
Mass = \(\int_a^b \delta\left|r^{\prime}(t)\right| d t\)
To find, we must differentiate this same given curve r ( t ) with respect to t to estimate |r'(t)|.
The given integration limits in this case are a = 0, b = 2π.
Now, as per the question;
The equation of the curve is given as;
r(t) = (4cost)i + (4sint)j + 4tk
Now, differentiate this same given curve r ( t ) with respect to t.
\(\begin{aligned}\left|r^{\prime}(t)\right| &=\sqrt{(-4 \sin t)^2+(4 \cos t)^2+4^2} \\&=\sqrt{16 \sin ^2 t+16 \cos ^2 t+16} \\&=\sqrt{16\left(\sin t^2+\cos ^2 t\right)+16}\end{aligned}\)
Further simplifying;
\(\begin{aligned}&=\sqrt{16(1)+16} \\&=\sqrt{16+16} \\&=\sqrt{32} \\\left|r^{\prime}(t)\right| &=4 \sqrt{2}\end{aligned}\)
Now, use integration to find the mass of the wire;
\(\begin{aligned}&=\int_a^b \delta\left|r^{\prime}(t)\right| d t \\&=\int_0^{2 \pi} 54 \sqrt{2} d t \\&=20 \sqrt{2} \int_0^{2 \pi} d t \\&=20 \sqrt{2}[t]_0^{2 \pi} \\&=20 \sqrt{2}[2 \pi-0] \\&=40 \pi \sqrt{2}\end{aligned}\)
Therefore, the mass of the wire is estimated as 40π√2 units.
To know more about density function, here
https://brainly.com/question/27846146
#SPJ4
The complete question is-
Find the mass of the wire that lies along the curve r and has density δ.
r(t) = (4cost)i + (4sint)j + 4tk, 0≤t≤2π; δ=5
An electrician charges a base fee of $70 plus $45 for each hour of work. The minimum the electrician charges is $160. Create a table that shows the amount the electrician charges for 1, 2, 3, and 4 hours of work. Determine the domain and range of the relation in context and explain whether or not this represents a function.
Answers
Answer:
1) See below for table.
2) Domain: \(\{1, 2, 3, 4\}\)
Range: \(\{160, 160, 205, 250\}\)
Yes, this is a function.
Step-by-step explanation:
We know that the electrician charges a base fee of $70 plus $45 for each hour of work.
We also know that the minimum the electrician charges is $160.
Let's write an equation. Let x denote the number of hours worked and y denote the total price. There's also a base fee of $70. So, we can write the following equation:
\(y=45x+75\)
Part 1)
Let's create our table for 1, 2, 3, and 4 hours. To do so, we simply need to substitute each value for x in our equation.
1 Hour:
We have:
\(y_1=45(1)+70\)
Multiply and add:
\(y_1=45+70=\$115\)
However, notice that the minimum the electrician charges is $160. Therefore, for one hour of work, the electrician will still charge $160. So:
\(y_1=\$160\)
2 Hours:
Substitute 2 for x:
\(y_2=45(2)+70=90+70=\$160\\\)
So:
\(y_2=\$160\)
3 Hours:
Substitute 3 for x:
\(y_3=45(3)+70=135+70=\$205\)
So:
\(y_3=\$205\)
4 Hours:
Substitute 4 for x:
\(y_4=45(4)+70=180+70=\$250\)
So:
\(y_4=\$ 250\)
Therefore, for 1, 2, 3, and 4 hours of work, the prices will be $160, $160, $205, and $250, respectively.
We can create the following table (please scroll down to see the table. Also, y is measured in dollars).
Part 2)
The domain of a relation are the input values.
In this context, our input values are the amount of hours worked, and we calculated for 1, 2, 3, and 4 hours of work.
Therefore, our domain in this context is:
\(\{1, 2, 3, 4\}\)
The range of a relation are the output values.
In this context, the output values are the price for x hours of work.
Therefore, our range in this context is:
\(\{160, 160, 205, 250\}\)
This relation does represent a function. Remember that a function cannot have repeating input values. In other words, no one input can be equal to two or more different outputs. However, one output can be mapped to two or more different inputs.
For our table, none of the inputs are repeating. So, our relation is a function.
And we're done!

Please explain how to write this in the horizontal model and the 3 other questions. Thank you! Sample Problem (remember the real"problem will be similar but could be presented differently Lau and LauLLC(LLLLC)builds swimming builds custom swimming pools in Boise,Idaho.LL LLC uses material reguisition forms and direct labor time tickets to trace direct materials and direct labor costs to specific jobs. Manufacturing overhead is applied to all jobs based on a percent of direct labor costs At the beginning of the second month of operations, the company had the following balances: oRaw Materials $75,000 Work in ProcessWIP) $140,000 Finished Goods -0- During the second month of operations (June 201XX),the company recorded the following transactions. aPurchased S225.000 in raw materials bssued the S150.000 of raw materials to production.of which S125.000 were direct materials cRecorded the following labor costspaid in cash) S60.000 in direct labor S40,000 in construction supervisorssalaries S26,000 in administrative salaries dRecorded the following actual manufacturing overhead costs oConstruction insurance 10,000 oConstruction equipment depreciation S55,000 Pool permits and inspections 9,000 eRecorded the $18.000 in selling and administrative costs. fApplied manufacturing overhead to jobs using 175%of direct labor costs gCompleted 16 pools at a total cost of S352,000.One1of these pools costingS22,000 is still waiting for final inspection and customer approval so the sale has not been finalized. hRealized sales revenue of S525.000 on the sale of the 15 pools that were sold Closed the Manufacturing Overhead account balance to Cost of Goods Sold. Required Questions: 1Draw the following t-accounts or colurmns and enter their beginning balances:Raw Materials WIP.Finished Goods,MOHCOGS if you find it helpful to draw SG&A Sales Revenue and Cash that is okay but not required). 2Record the transactions listed above and calculate the ending balances for all accounts 3)How much is manufacturing overhead over or underapplied? 4What isthe adiusted ending balance for CostofGoods Sold
Answers
(3) Add: Under applied overhead 34,000
(4) Adjusted cost of goods sold 364,000
1 and 2 RAW MATERIAL INVENTORY
Beginning balance 75,000
a 225,000 150,000 b, Ending Balance 150,000
WORK IN PROGRESS INVENTORY
Beginning balance 140,000
b 125,000 352,000 g
c 60,000
f 105,000
j Ending Balance 78,000
FINISHED GOODS INVENTORY
Beginning balance -
g 352,000 330,000 h
Ending Balance 22,000
FACTORY OVERHEAD
b 25,000
c 40,000 105,000 f
d 74,000
Ending Balance 34,000
COST OF GOODS SOLD
h 330,000
Ending Balance 330,000
Factory overhead applied on the basis of direct labor cost .
Hence applied overhead = 60,000 x 175% = $105,000Step: 2
3)
Computation of under /(over) applied OH
Actual OH($) Applied OH ($) Under /(over) applied OH ($)
139,000 105,000 34,000
Actual manufacturing overhead:
$
Indirect material 25,000
Indirect Labour 40,000
Other manufacturing overhead 74,000
139,000
4)
Cost of goods sold (Unadjusted) 330,000
Add: Under applied overhead 34,000
Adjusted cost of goods sold 364,000
Actal manufacturing overhead is more than applied overhead,it means factory overhead under applied and it will be added in unadjusted cost of goods sold to ascertain adjused cost of goods sold.
Learn more about Material here:
https://brainly.com/question/32807748
#SPJ4
round to nearest thousandth
0.227
Answers
Answer:
is there another number after the 7 if so if it is 5 or bigger it rounds up but 1-4 rounds down
Step-by-step explanation:
Answer:
0.23!! =D
hundredths (1/100)
I need help with this question. Determine if each trinomial is a perfect square trinomial. Write yes or no if yes factor it.

Answers
Solution
Perfect square trinomials are algebraic expressions with three terms that are obtained by multiplying a binomial with the same binomial.
To determine if the trinomials in the question is a perfect trinomial, we will factor each of the trinomials and then decide which is a perfect trinomial
\(\begin{gathered} m^2-6m+9 \\ \rightarrow m^2-3m-3m+9 \\ \rightarrow m(m-3)-3(m-3) \\ \rightarrow(m-3)(m-3) \\ \rightarrow(m-3)^2 \end{gathered}\)The first trinomial above is a perfect trinomial
\(\begin{gathered} 9n^2+30n+25 \\ \rightarrow9n^2+15n+15n+25 \\ \rightarrow3n(3n+5)+5(3n+5) \\ \rightarrow(3n+5)(3n+5) \\ \rightarrow(3n+5)^2 \end{gathered}\)The second trinomial above is a perfect trinomial
\(\begin{gathered} 2w^2-4w+9 \\ can\text{ not be farctored} \end{gathered}\)The third trinomial above is not a perfect trinomial
\(\begin{gathered} 4d^2-4d+1 \\ \rightarrow4d^2-2d-2d+1 \\ \rightarrow2d(2d-1)-1(2d-1) \\ \rightarrow(2d-1)^2 \end{gathered}\)The fourth trinomial above is a perfect trinomial
The summary of the solution is given below
\(\begin{gathered} m^{2}-6m+9 \\ Yes \\ Factor\rightarrow(m-3)^2 \end{gathered}\)\(\begin{gathered} 9n^{2}+30n+25 \\ Yes \\ Factor\rightarrow(3n+5)^2 \end{gathered}\)\(\begin{gathered} 2w^{2}-4w+9 \\ No \\ Factor\rightarrow none \end{gathered}\)\(\begin{gathered} 4d^2-4d+1 \\ Yes \\ Factor\rightarrow(2d-1)^2 \end{gathered}\)