A group of 10 friends are in line to see a movie. It cost $15 for 3 people to see a movie. How much will the group pay?​

Answer: b=-2

Step-by-step explanation:

3(b+3)-4(-2+b)=19

3b+9+8-4b=19

-b+17=19

-b=19-17

-b=2

-b/-1=2/-1

b=-2

Answer: m24+70

Step-by-step explanation: A. Triangle C'D'E' is a translation of triangle ... C. Sides DE and D'E' have the same length. D. Each vertex is translated 4 units to ... C. ZB and B' are congruent angles. ... She will rotate the figure 90° clockwise, 180°, and then 90° counterclockwise. ... Which angles have the same measure ... The m24 = 70° What is the m27?

Answer:

52+n=m

Step-by-step explanation:

Answer:

6.5 /52 m = n

Step-by-step explanation:

The rate is 6.5 miles / 52 minutes

We are going to run m miles in n minutes

m = 6.5 / 52 * n

We want to solve for n

Multiply each side by 52/ 6.5

6.5 /52 m = 6.5 / 52 * n * 6.5 / 52

6.5 /52 m = n

Answer:

15,500 hits in £31

Step-by-step explanation:

First you want to find out how many hits can be made in £1.

£2 = 1000 hits

£1 = 500 hits

then you want to find £31 for you times it by 31 to find out the hit

31 X 500= 15,500

Hoped this helps :)

Answer:

15,500

Step-by-step explanation:

For every 1000 hits, you get $2. So divide 31 by 2 (15.5) and multiply that by 1000.

Either that, or divide 1000 by 2 (500) meaning you get $1 for every 500 views. Then you can multiply that by 31.

Answer:

m+6n+5

Step-by-step explanation:

Let's simplify step-by-step.

m+8+6n−3

=m+8+6n+−3

Combine Like Terms:

=m+8+6n+−3

=(m)+(6n)+(8+−3)

=m+6n+5

We can say that the tree's height increased by 12.5% over the course of the six-week experiment.

To calculate the percent increase in the tree's height, we need to find the difference between its new height and its old height, and then express that difference as a percentage of the old height.

We start with the formula:

percent increase = (new value - old value) / old value * 100%

In this case, the old value is the height of the tree at the beginning of the experiment, which is 32 inches. The new value is the height of the tree six weeks later, which is 36 inches.

So, plugging in those values, we get:

percent increase = (36 - 32) / 32 * 100%

Simplifying this expression gives us:

percent increase = 4 / 32 * 100%

And when we evaluate that expression, we get:

percent increase = 12.5%

Therefore, the percent increase in the tree's height is 12.5%.

To learn more about tree's height please click on below link        

https://brainly.com/question/25659489

#SPJ1

Triangle A- Obtuse, it has an angle over 90 degrees.

Triangle B- Acute, all of its angles are under 90 degrees.

Triangle C- Right, it has a 90 degree angle.

Triangle D- Obtuse, it has an angle over 90 degrees.

Answer:

Triangle A: Obtuse

Triangle B: Acute

Triangle C: Right

Triangle D: Obtuse

Step-by-step explanation:

Answer:

A

Step-by-step explanation:

Answer:

Another rational number

Using the given information, the total distance travelled by the golf ball is 288 m

From the question, we are to calculate the total distance travelled by the golf ball

The distance travelled by the golf ball can be calculated by using the formula,

Distance = Speed × Time

From the given information,

The golf ball rolls at a speed of 8 m/s for 12 seconds

Thus,

The distance travelled at this time is

Distance = 8 m/s × 12 s

Distance = 96 m

Also,

Mandy hits the golf ball and it rolls for 16 seconds at a speed of 12 m/s

The distance travelled at this time is

Distance = 12 m/s × 16 s

Distance = 192 m

The total distance travelled by the golf ball is 96 m + 192 m

=

Hence, the total distance travelled by the golf ball is 288 m

Learn more on Calculating total distance here: https://brainly.com/question/11607177

#SPJ1

The sale price of the shoe is given as follows:

P3,436.

The sale price of the shoe is obtained applying the proportions in the context of the problem.

The initial price is of:

P 4,295.

The shoe is sold at a discount of 20%, meaning that the sale price is 80% of the initial price, and the value is given as follows:

0.8 x 4295 = P3,436.

The problem asks for the selling price of the shoe.

More can be learned about proportions at https://brainly.com/question/24372153

#SPJ1

Answer:

x=5

Step-by-step explanation:

Answer:

The median is 6.5

===================================================

Explanation:

The down payment and trade-in value add to 4000+6500 = 10,500

Subtract this total from the car's cost

42,100 - 10,500 = 31,600

This is the amount loaned to the customer.

---------------

We have these input values

Let's compute the monthly payment

P = (L*i)/(1 - (1+i)^(-n))

P = (31600*0.00375)/(1 - (1+0.00375)^(-60))

P = 589.119408031938 approximately

P = 589.12

The number of ways you can draw n chords in a circle combination with 2 x n points such that no 2 chords intersect is n! / (2! * (n - 2)!).

Given a number n, the number of ways you can draw n chords in a circle with 2 * n points such that no two chords intersect is given by n choose 2. This is because you have 2 * n points, and for each chord, you must choose two of these points to be its endpoints.

The number of ways to choose two points out of 2 * n points is given by the binomial coefficient (n choose 2), which is equal to n! / (2! * (n - 2)!). This formula counts the number of combinations of n chords that can be drawn in a circle without any intersections.

Learn more about binomial coefficient:

https://brainly.com/question/13243530

#SPJ4

In domain and range of a relation, if R be a relation from set A to set B, then

• The set of all first components of the ordered pairs belonging to R is called the domain of R.

Thus, Dom(R) = {a ∈ A: (a, b) ∈ R for some b ∈ B}.

• The set of all second components of the ordered pairs belonging to R is called the range of R.

Thus, range of R = {b ∈ B: (a, b) ∈R for some a ∈ A}.

Therefore, Domain (R) = {a : (a, b) ∈ R} and Range (R) = {b : (a, b) ∈ R}

Answer:

It is possible, because the two shortest sides have to add up to be more than the longest side, and 8 + 12 = 20, which is more than the longest side of 17.

So yes, I agree with Bear.

Answer:

Step-by-step explanation:

x+9

Let x, be 4

4+9=13

given condition,

x+9<4x

4+9<4(4)

13<16

The answer is:

Work/explanation:

Our inequality is:

\(\sf{x+9 < 4x}\)

Flip it

\(\sf{4x > x+9}\)

Solve

\(\sf{4x-x > 9}\)

Combine like terms

\(\sf{3x > 9}\)

Divide each side by 3

\(\sf{x > 3}\)

The particle travels approximately 45.63 units along the path. The displacement is the straight-line distance between the initial and final positions of the particle is 2781.

To find the distance the particle travels along the path, we can integrate the speed over the interval of time. The speed of the particle is given by the magnitude of its velocity vector.

The velocity vector is the derivative of the position function r(t):

\(v(t) = (d/dt)(t^3/3, t^2, 2t)\)

\(= (t^2, 2t, 2)\)

The speed of the particle at any given time t is:

|v(t)| = √((t^2)^2 + (2t)^2 + 2^2)

= √(t^4 + 4t^2 + 4)

= √((t^2 + 2)^2)

To find the distance traveled along the path, we integrate the speed function over the given interval of time. The particle travels from t = -1/3 to t = 9.

distance = ∫[from -1/3 to 9] |v(t)| dt

= ∫[from -1/3 to 9] |t^2 + 2| dt

= ∫[from -1/3 to 0] -(t^2 + 2) dt + ∫[from 0 to 9] (t^2 + 2) dt

= [-1/3 * t^3 - 2t] (from -1/3 to 0) + [1/3 * t^3 + 2t] (from 0 to 9)

Evaluating the definite integrals:

distance = [-1/3 * 0^3 - 2 * 0 - (-1/3 * (-1/3)^3 - 2 * (-1/3))] + [1/3 * 9^3 + 2 * 9 - (1/3 * 0^3 + 2 * 0)]

= [0 - (1/3 * (-1/27) + 2/3)] + [1/3 * 729 + 18]

= [1/27 + 2/3] + [729/3 + 18]

= 1/27 + 2/3 + 729/3 + 18

= 1/27 + 18/27 + 729/3 + 18

= (1 + 18 + 729)/27 + 18

= 748/27 + 18

= 27.63 + 18

= 45.63 units (approximately)

Therefore, the particle travels approximately 45.63 units along the path.

To find the average speed, we divide the distance traveled by the time taken. The time taken is 9 - (-1/3) = 9 1/3 = 28/3.

average speed = distance / time

= 45.63 / (28/3)

= 45.63 * (3/28)

= 4.9179 units per unit time (approximately)

The displacement is the straight-line distance between the initial and final positions of the particle.

displacement = |r(9) - r(-1/3)|

= |(9^3/3, 9^2, 2 * 9) - ((-1/3)^3/3, (-1/3)^2, 2 * (-1/3))|

= |(27, 81, 18) - (-1/27, 1/9, -2/3)|

= |(27 + 1/27, 81

= 2781.

For more such questions on displacement , Visit:

https://brainly.com/question/1581502

#SPJ11

Answer:

The correct answer would be A) on edge.

Step-by-step explanation:

Edge 2021.

Answer:  The correct answer is A

Step-by-step explanation:

If your multiplying fractions you take the first fraction 1/4 and the number 5, but you turn that into a fraction so now it's 5/1, and you multiply them together to get 5/4

1/4 x 5/1 = 5/4

✩brainliest appreciated ✩

Answer:

Here's a tree diagram to represent all of the possible outcomes for the coin landing on red or on yellow:

   / Red \

   /        \

  /          \

Start         End

  \          /

   \        /

     \Yellow/

The "Start" node represents the beginning of the experiment, and it has two branches: one for the coin landing on red, and one for the coin landing on yellow. The branches lead to the "Red" and "Yellow" nodes, respectively, which represent the possible outcomes. Finally, each outcome leads to the "End" node, which represents the end of the experiment.

For the fractions, the calculation of 3/5 of 2/3 of 3/4 of 560 is equal to 168.

To calculate 3/5 of 2/3 of 3/4 of 560, break it down step by step:

Step 1: Calculate 3/4 of 560:

3/4 × 560 = (3 × 560) / 4 = 1680 / 4 = 420

Step 2: Calculate 2/3 of the result from Step 1:

2/3 × 420 = (2 × 420) / 3 = 840 / 3 = 280

Step 3: Calculate 3/5 of the result from Step 2:

3/5 × 280 = (3 × 280) / 5 = 840 / 5 = 168

Therefore, 3/5 of 2/3 of 3/4 of 560 is equal to 168.

Find out more on fractions here: https://brainly.com/question/78672

#SPJ1

Answer:

-729

Step-by-step explanation:

sequence is to multiply by -3 to get next term

The 99% confidence interval for the population proportion p is (0.776, 0.824).

To find the 99% confidence interval for a proportion, we can use the formula:

CI = p^ ± z*(SE)

where p^ is the sample proportion, SE is the standard error, and z is the critical value from the standard normal distribution corresponding to the level of confidence.

For a 99% confidence interval, the critical value z is 2.576.

Substituting the given values into the formula, we have:

CI = 0.80 ± 2.576*(0.03/√200)

Simplifying this expression, we have:

CI = 0.80 ± 0.024

This means that we are 99% confident that the true population proportion falls between 0.776 and 0.824. We can interpret this interval as a range of plausible values for the population proportion, based on the sample data.

To learn more about confidence interval here:

https://brainly.com/question/24131141

#SPJ1

The probability that the student got an 'A' given they are male is approximately 0.12 or 12%.

To find the probability that a student got an 'A' given they are male, we need to use Bayes' theorem:

P(A | Male) = P(Male | A) × P(A) / P(Male)

We can find the values of the terms in the formula using the information given in the table:

P(Male) = (25/54) = 0.46 (the proportion of all students who are male)

P(A) = (17/54) = 0.31 (the proportion of all students who got an 'A')

P(Male | A) = (3/17) = 0.18 (the proportion of all students who are male and got an 'A')

Therefore, plugging these values into the formula:

P(A | Male) = 0.18 × 0.31 / 0.46

P(A | Male) ≈ 0.12

So the probability that the student got an 'A' given they are male is approximately 0.12 or 12%.

for such more question on probability

https://brainly.com/question/13604758

#SPJ11

Answer: We have f(x)=3x⁵+6x²-5 and g(x)= 2x⁴+7x²-x+16

                        (f-g)(x)= 3x⁵-2x⁴-x²+x-21

Step-by-step explanation:

Here we have,

Given : f(x)=3x⁵+6x²-5 and g(x)= 2x⁴+7x²-x+16

We know,

(f-g)(x)= f(x)-g(x)

= (3x⁵+6x²-5 ) - ( 2x⁴+7x²-x+16)

On subtracting g(x) from f(x) we get,

(f-g)(x)= (3x⁵+6x²-5  - 2x⁴-7x²+x-16)

On simplify,

 (f-g)(x) =3x⁵-2x⁴-x²+x-21

Hence,

(f-g)(x) = f(x) - g(x) = 3x⁵-2x⁴-x²+x-21

To see more related questions follow the link:

https://brainly.com/question/30721594

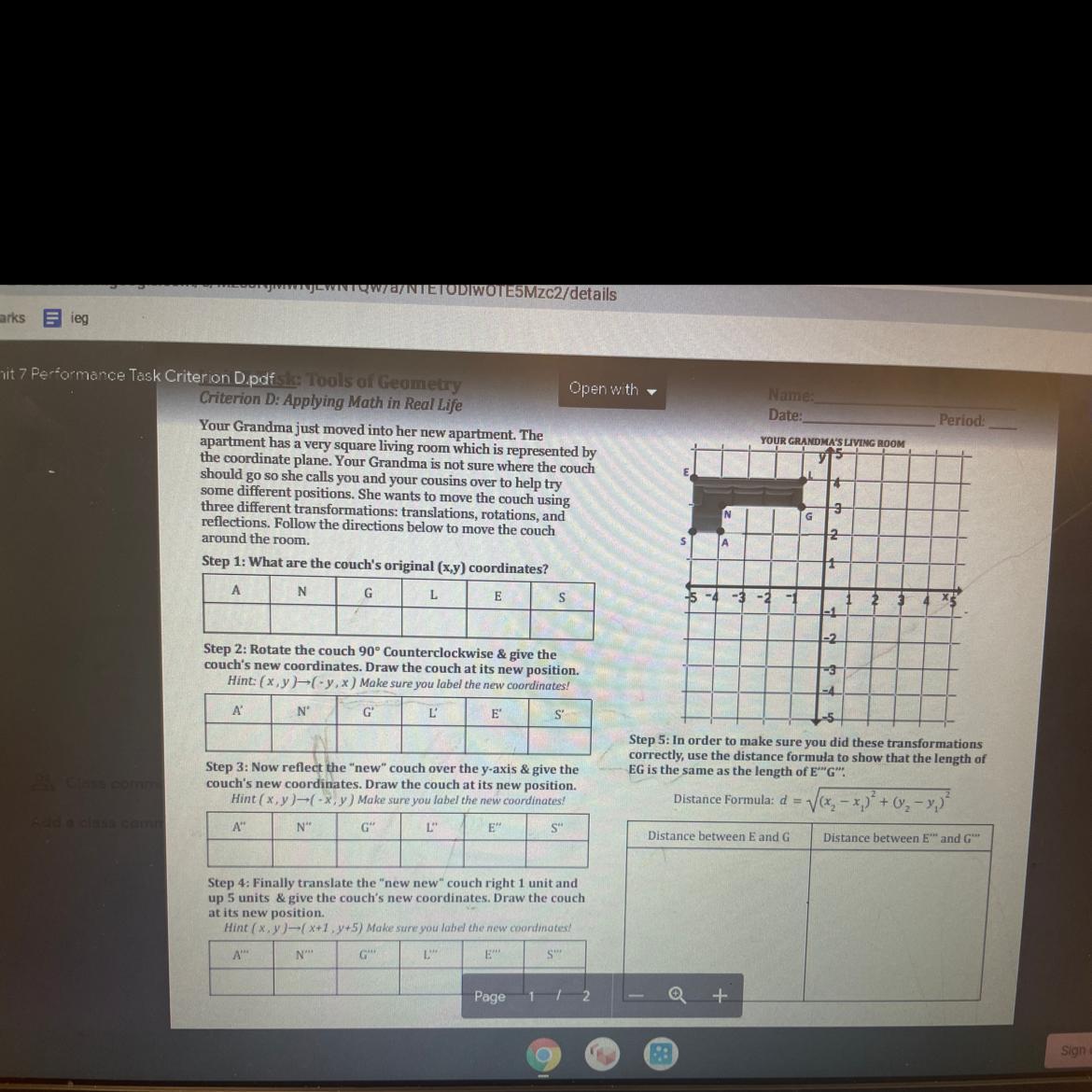
Answer:

Step-by-step explanation:

Step 1: What are the couch's original coordinates?

Step 2: Rotate the couch 90° counterclockwise.

Rule: (x, y) → (-y, x)

Step 3: Now reflect the "new" couch over the y-axis.

Rule: (x, y) → (-x, y)

Step 4: Finally translate the new new" couch right 1 unit and up 5 units.

Rule: (x + 1, y + 5)

Step 5: Use the distance formula to show that the length of EG is the same as the length of E'''G'''.

Distance between E(-5, 4) and G(-1, 3)

\(\large \textsf {d = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$}\\\\\large \textsf {d = $\sqrt{(-1-(-5))^2+(3-4)^2}$}\\\\\large \textsf {d = $\sqrt{(-1+5)^2+(3-4)^2}$}\\\\\large \textsf {d = $\sqrt{4^2+(-1)^2}$}\\\\\ \large \textsf {d = $\sqrt{16+1}$}\\\\\large \textsf {d = $\sqrt{17}$}\\\\\large \textsf {d = ${4.12}$}\)

Distance between E'''(5, 0) and G'''(4, 4)

\(\large \textsf {d = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$}\\\\\large \textsf {d = $\sqrt{(4-5)^2+(4-0)^2}$}\\\\\large \textsf {d = $\sqrt{(-1)^2+4^2}$}\\\\\large \textsf {d = $\sqrt{1+16}$}\\\\\ \large \textsf {d = $\sqrt{17}$}\\\\ \large \textsf {d = ${4.12}$}\)

This means that the length of EG is the same as the length of E'''G'''.

Hope this helps!

Answer:

To find the area of a regular octagon with a side length of 4 cm and an apothem of approximately 3.5 cm, we can use the formula:

Area = (1/2) × (apothem) × (perimeter)

The perimeter of a regular octagon can be calculated as:

Perimeter = 8 × (side length) = 8 × 4 cm = 32 cm

Therefore, the area of the octagon can be calculated as:

Area = (1/2) × (3.5 cm) × (32 cm) = 56 cm²

So, the area of the regular octagon is 56 square centimeters.