A graduate student is performing a study on a new antidepressant. The drug is supposed to reduce depression, but the graduate student realizes that it may do nothing or even increase depression, so she decides to formulate nondirectional hypotheses and conduct a two-tailed test. First, she uses mu_general population to denote the average score on the depression inventory for the population of all depressed people, and mu_antidepressant to denote the average score on the depression inventory for the population of depressed people who take the new antidepressant. She knows that the average score for all depressed people is mu_general population = 25, with a standard deviation of sigma = 6. The graduate student identifies the null and alternative hypotheses as: H_0: mu_antidepressant = mu_general population H_1: mu_antidepressant notequalto mu_general population The sample of 36 depressed people who tried out the new antidepressant scored an average of 23.3. Since the graduate student knows the standard deviation of the scores on the depression inventory for the population of people who are depressed, she intends to use a hypothesis test that uses the z-score of the sample mean as the test statistic (also known as the z test). First, she wants to make sure all the required assumptions are satisfied. Which of the following conditions is not a required assumption for the z test?
The scores on the depression inventory follow a normal distribution or the sample size is large (at least 30).
The standard deviation of the scores on the depression inventory is the same for those who take the antidepressant and those who don't.
Each observation is independent of every other observation.
The sample size must be very large.
Members of the sample are selected randomly.
Use the Distributions tool to find the critical region for alpha = .05. The critical z-scores (the values for z-scores that separate the tails from the main body of the distribution, forming the critical regions) are_______
Calculate the z statistic, and use the Distributions tool to evaluate the null hypothesis. The z statistic is______ The z statistic_______ lie in the critical region for a two-tailed hypothesis test. Therefore, the null hypothesis is______ .
Answers
Answer:
Step-by-step explanation:
From the given information:
The null and the alternative hypothesis is:
\(H_o: \mu_{antidepressant}= \mu_o\)
\(H_1: \mu_{antidepressant}\ne \mu_o\)
The population mean = 25
The sample mean = 23.3
sample size n = 36
standard deviation = 6
From the following conditions given; the condition that is not required is:
\(\text{The sample size must be very large}\)
Since the sample size is 30, we do not need the condition and it's enough for the Z test provided that the population is not normally distributed. If the population is distributed normally, then any sample size is valid:
Then, the test statistics can be computed as follows:
\(Z = \dfrac{X - \mu}{\dfrac{\sigma}{\sqrt{n}} }\)
\(Z = \dfrac{23.3 - 25}{\dfrac{6}{\sqrt{36}} }\)
\(Z = \dfrac{23.3 - 25}{\dfrac{6}{6} }\)
\(Z = -1.7\)
At the level of significance 0.05
Since the test is two-tailed, the critical value \(Z_{\alpha/2} = Z_{0.025} = 1.96\)
Provided that the Z value is not less than the critical value;
Then, we fail to reject the null hypothesis.
We conclude that there is no enough evidence that the drug reduces depression.

Related Questions
Evaluate the piecewise function


Answers
The solution of the composite function fog(x) = 3x + 3 at x > 2.
What is composite function?Let the two function f(x) and g(x) generate a new function h(x) using an operation.
The operation is composition of functions and h(x) is a composite function.
We have three piecewise function.
First we have to show that,
the composite function,
fog(x) at x > 2.
For that,
g(x) at x > 2 is,
g(x) = 3x.
Now, f(g(x)),
= f(3x)
= 3x + 3 at x > 2.
Therefore, the function is fog(x) = 3x + 3.
To learn more about the composite function;
https://brainly.com/question/29048585
#SPJ1
The complete question:
Find the fog(x) at x > 2
I need help finding the m

Answers
(I think)
Would you like me to explain how I got that angle?
Solve a two step equation and identify the steps to equals 2= -7/4+1/4 X
Answers
Answer:
x = 15
Step-by-step explanation:
Step 1: Write out equation
1/4x - 7/4 = 2
Step 2: Add 7/4 to both sides
1/4x = 15/4
Step 3: Divide both sides by 1/4
x = 15
Find the value of
n
(
√
5
)
5
=
5
n
Answers
Answer:
n = 26
Step-by-step explanation:
Solve the rational equation by combining expressions and isolating the variable
n.
Can anyone help me out on this
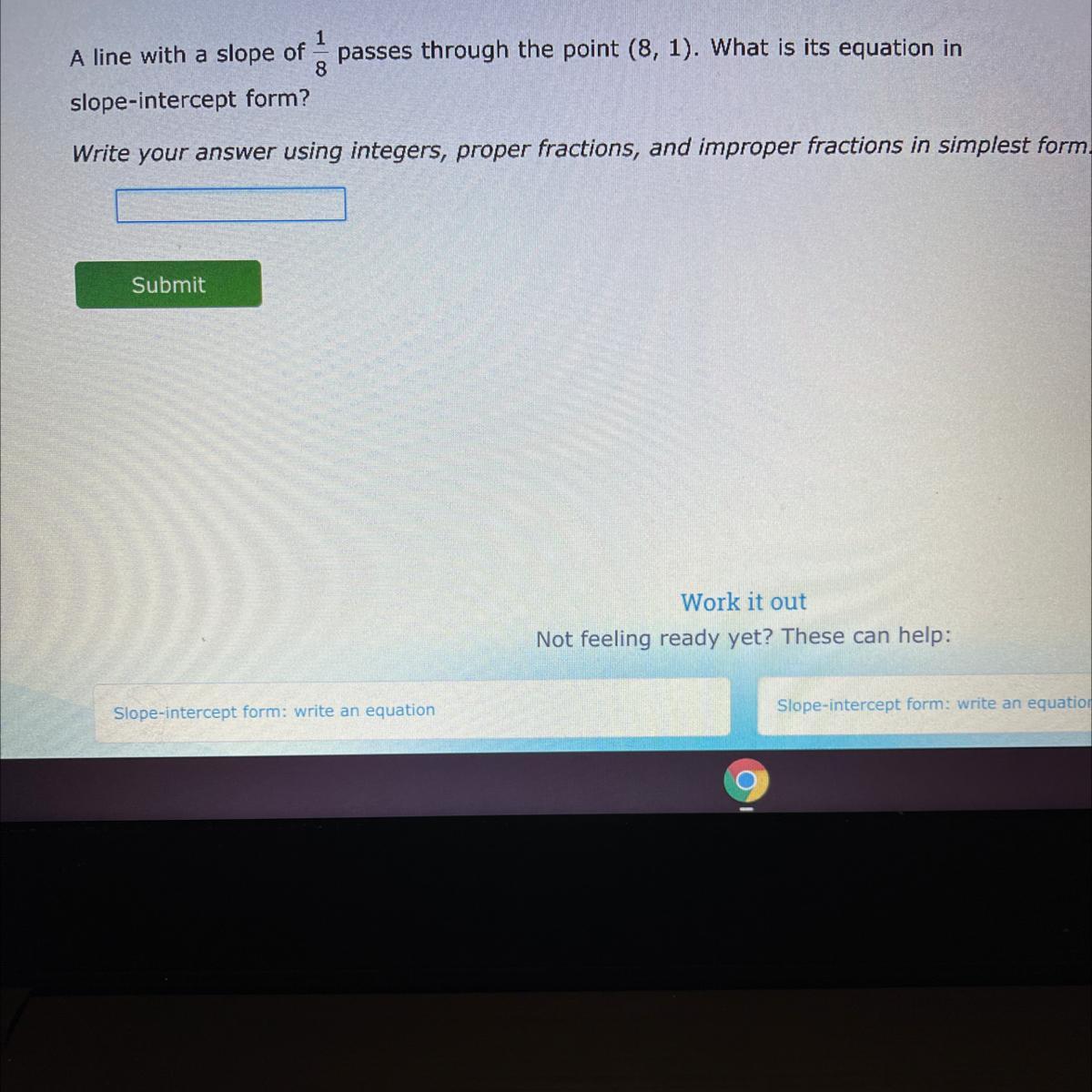
Answers
Answer: y = 1/8x+1
y=mx+b is slope intercept form
given m = 1/8 and a point we can find b by plugging in what we have
1=1/8(8)+b
1=1b
b=1
So then we know m = 1/8 and b = 1
y=1/8x+1 is the answer
how to find the degree of a term
Answers
Degree of a term is the exponents of a variable , if a term have two variables then the degree of a term is the sum of the exponents of the variables.
Degree of a term:
The degree of an individual term of a polynomial is the exponent of its variable.
Examples:
1) \(2x^3\)
here exponent of variable x is 3.
so the degree = 3
2) \(5x^5y^4\)
sum of exponent of variables x and y is = 5+4 = 9
so the degree = 9
3) \(x^2y^3\)
sum of exponent of variables x and y is = 2+3 = 5
so the degree = 5
Learn more about the degree of a term here:
https://brainly.com/question/23992956
#SPJ4
Fill in the blank to find the y-intercept.
(0,_____)

Answers
Answer:
-2
Step-by-step explanation:
Answer:
-2
Step-by-step explanation:
the y intercept is the point on the graph where the line crosses the x axis
Two vectors and are given by and . If these two vectors are drawn starting at the same point, what is the angle between them
Answers
Answer: hello your question is incomplete below is the complete question
The Two vectors; A = 5i + 6j +7k and B = 3i -8j +2k.
answer;
angle = 102°
Step-by-step explanation:
multiplying the vectors
A.B = |A| * |B|* cosθ
hence : Cosθ = (Ai*Bi )+ (Aj*Bj) + ( Ak*Bk/ (√A^2 *√B^2 )
= 15 - 48 + 14 /(√25+26+29) * (√9+64+4)
= -0.206448454
θ = cos^-1 ( -0.206448454) = 101.9° ≈ 102°
The area model shows 2 1 4
What is 2 x 2 1/4?
2 1/2
2 3/4
4 1/4
4 1/2
Answers
Answer:
4 1/2
Step-by-step explanation:Because 2x2 =4 and 2x1/4 = 1/2 so it is 4 1/2
For each of the following questions, say whether the random process is reasonably a binomial process or not, and explain your answer. If it is not a binomial process, explain what assumptions are not well met. If it is a binomial process, comment on the validity of each of things that must be true for a process to be a binomial process (ex: identify n: the number of Bernoulli trials, # the probability of success, etc).
a. A fair die is rolled until a 1 appears, and X denotes the number of rolls.
b. Twenty of the different Badger basketball players each attempt 1 free throw and X is the total number of successful attempts.
c. A die is rolled 50 times. Let X be the face that lands up.
d. In a bag of 10 batteries, I know 2 are old. Let X be the number of old batteries I choose when taking a sample of 4 to put into my calculator.
e. It is reported that 20% of Madison homeowners have installed a home security system. Let X be the number of homes without home security systems installed in a random sample of 100 houses in the Madison city limits.
Answers
Answer:
can u help me with my answer
Step-by-step explanation:
1x1 the answer is a
Using the information in the Box-and-Whisker plot shown, below what value is three quarters of the data?
A. 7
B. 10
C. 12
D. 17
Answers
Answer:
Step-by-step explanation:
A
7. The probability that a randomly chosen student will be left-handed is .09: a) In a class of 108, find the probability that there will be (exactly) 8 left-handed students. b) The classroom has 12 desks designed for people who are left-handed. Use an appropriate approximate method to find the probability that there are enough for all the left-handed students.
Answers
Solution :
Let x be student will be left handed
P = 0.09
Using the normal approximation to binomial distribution,
a). n = 108,
μ = np = 9.72
\($\sigma = \sqrt{np(1-p)}$\)
\($=\sqrt{8.8452}$\)
= 2.9741
Required probability,
P(x=8) = P(7.5 < x < 8.5)
\($=P\left(\frac{7.5-9.72}{2.9741}< \frac{x-\mu}{\sigma}< \frac{8.5-9.72}{2.9741}\right)$\)
\($=P(-0.75 < z < -0.41)$\)
Using z table,
= P(z<-0.41)-P(z<-0.75)
= 0.3409-0.2266
= 0.1143
b). P(x=12) = P(11.5 < x < 12.5)
\($=P\left(\frac{11.5-9.72}{2.9741}< \frac{x-\mu}{\sigma}< \frac{12.5-9.72}{2.9741}\right)$\)
\($=P(0.60 < z < 0.94)$\)
Using z table,
= P(z< 0.94)-P(z< 0.60)
= 0.8294 - 0.7257
= 0.1006
Point K is located at ( 1 , 2 ) on the following coordinate plane. A square that has a perimeter of 20 units will be drawn so that K is one vertex of the square. Which three ordered pairs could represent the location of another vertex of the square? Select the three correct answers.
Answers
Three ordered pairs that could represent the location of another vertex of the square are (7, 2), (-5, 2), (1, 8).
To find the possible locations of the other vertices of the square, we need to determine the distance from point K to any other vertex of the square. Since the perimeter of the square is 20 units, each side of the square has a length of 20/4 = 5 units.
One way to find the other vertices is to draw a circle with center at K and radius 5 units, and then look for points on the circle that have integer coordinates. Alternatively, we can use the distance formula to calculate the distance from K to another point (x, y), which must be 5 units, and then solve for y in terms of x.
Using the distance formula, we get:
\(\sqrt{(x-1)^{2} +(y-1)^{2} }\) = 5
Simplifying and squaring both sides, we get:
(x-1)^2 + (y-2)^2 = 25
Expanding the left side and simplifying, we get:
\(x^{2}\) - 2x + \(y^{2}\) - 4y + 20 = 0
Completing the square for x and y, we get:
\((x-1)^{2}\) + \((y-1)^{2}\) = \(6^{2}\)
This is the equation of a circle with center at (1, 2) and radius 6 units. Any point on this circle that has integer coordinates could be a vertex of the square, since it will be exactly 5 units away from K.
Using this method, we can find several possible locations of the other vertices of the square. Three of them are:
(7, 2), (-5, 2), (1, 8)
To learn more about vertex here:
https://brainly.com/question/30940247
#SPJ1
How much space will a cylindrical water tank occupy if its height is 100 cm and its diameter is 30
find the volume

Answers
Answer:
volume of a cylindrical water tank = 70,650cm³
Step-by-step explanation:
volume of cylinder, V = πr²h
where π = 3.14
h = 100cm
r = ?
given is diameter = 30cm
r = d/2 = 30/2 = 15cm
substituting the values in the formula,
V = 3.14 * 15² * 100
= 3.14 * 225 * 100
= 70,650cm³
Answer:
How much space it would take up: 706.86 square centimeters of floor space and extend vertically to a height of 100 cm
Volume: 706,500 cm³
Step-by-step explanation:
How much space it would take up:
To determine the space occupied by a cylindrical water tank in a room, we need to consider its dimensions and the area it covers on the floor.
The diameter of the tank is given as 30 cm, which means the radius is half of that, 15 cm.
To calculate the space it occupies on the floor, we need to find the area of the circular base. The formula for the area of a circle is A = πr², where A is the area and r is the radius.
A = π(15 cm)²
A = π(225 cm²)
A ≈ 706.86 cm²
So, the circular base of the tank occupies approximately 706.86 square centimeters of floor space.
The height of the tank is given as 100 cm, which represents the vertical space it occupies in the room.
Therefore, the cylindrical water tank would take up 706.86 square centimeters of floor space and extend vertically to a height of 100 cm in the room.
Volume:
To calculate the volume of a cylindrical water tank, we can use the formula V = πr²h, where V is the volume, r is the radius, and h is the height.
First, we need to find the radius by dividing the diameter by 2:
Radius = 30 cm / 2 = 15 cm
Now we can calculate the volume:
V = π(15 cm)²(100 cm)
V = 3.14 * 225 cm² * 100 cm
V = 706,500 cm³
Therefore, the cylindrical water tank will occupy a volume of 706,500 cm³ or 706.5 liters.
-1/4 plus 3/5
Answer or else
Answers
The algebric expression -1/4 + 3/5 is equal to 7/20 when simplified.
To solve the expression -1/4 + 3/5, we need to find a common denominator for the fractions and then perform the addition.
The common denominator for 4 and 5 is 20. We can rewrite the fractions with this denominator:
-1/4 = -5/20
3/5 = 12/20
Now that the fractions have the same denominator, we can add them:
-5/20 + 12/20 = (-5 + 12)/20 = 7/20
Therefore, -1/4 + 3/5 is equal to 7/20.
To further simplify the fraction, we can check if there is a common factor between the numerator and denominator. In this case, 7 and 20 have no common factors other than 1, so the fraction is already in its simplest form.
Thus, the final answer is 7/20.
For more such question on algebric expression. visit :
https://brainly.com/question/4344214
#SPJ8
what is 1/5 - 3/4
thank you for your answer
btw I am on edg
Answers
Answer:
-11/20 or -0.55
Step-by-step explanation:
1/5 = 4/20
3/4 = 15/20
4/20 - 15/20 = -11/20
Answer:
- 11/20
or
-0.55
Step-by-step explanation:
PLZ MRAK ME BRAINLIEST
Rewrite the equation 8r+62 - 7 = 2 in standard form and Identify a, b, and c
Answers
Answer:
a = 0
b = 8
c = 53
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightEquality Properties
Algebra I
Standard Form: ax² + bx + c = 0Step-by-step explanation:
Step 1: Define
8r + 62 - 7 = 2
Step 2: Rewrite
Add: 8r + 55 = 2Subtract 2 on both sides: 8r + 53 = 0Step 3: Identify Variables
a = 0
b = 8
c = 53
Find the equation of a line parallel to y=x−1 that contains the point (−3,−2). Write the equation in slope-intercept form.
Answers
Answer:
y = x + 1
Step-by-step explanation:
Parallel lines have same slope.
y = x - 1
Compare with the equation of line in slope y-intercept form: y = mx +b
Here, m is the slope and b is the y-intercept.
m =1
Now, the equation is,
y = x + b
The required line passes through (-3 ,-2). Substitute in the above equation and find y-intercept,
-2 = -3 + b
-2 + 3 = b
\(\boxed{b= 1}\)
Equation of line in slope-intercept form:
\(\boxed{\bf y = x + 1}\)
The equation is :
↬ y = x + 1Solution:
We KnowIf two lines are parallel to each other, then their slopes are equal. The slope of y = x - 1 is 1. Hence, the slope of the line that is parallel to that line is 1.
We shouldn't forget about a point on the line : (-3, -2).
I plug that into a point-slope which is :
\(\sf{y-y_1=m(x-x_1)}\)
Slope is 1 so
\(\sf{y-y_1=1(x-x_1)}\)
Simplify
\(\sf{y-y_1=x-x_1}\)
Now I plug in the other numbers.
-3 and -2 are x and y, respectively.
\(\sf{y-(-2)=x-(-3)}\)
Simplify
\(\sf{y+2=x+3}\)
We're almost there, the objective is to have an equation in y = mx + b form.
So now I subtract 2 from each side
\(\sf{y=x+1}\)
Hence, the equation is y = x + 1Sum the following numbers then divide by 5
( 3 + 5 + 6 + 2 + 4 ) /5 } = ? What is your answer ?
Answers
Answer:
4
Step-by-step explanation:
(3+5+6+2+4) / 5 = ?
(20) / 5 = 4
Can someone help me and can y’all show me how you got the answer

Answers
Answer:
x = -8
Step-by-step explanation:
Step 1: Write equation
1/2x + 13 = 9
Step 2: Solve for x
Subtract 13 on both sides: 1/2x = -4Multiply both sides by 2: x = -8Step 3: Check
Plug in x to verify it's a solution.
1/2(-8) + 13 = 9
-4 + 13 = 9
9 = 9
Answer:
-8
Step-by-step explanation:
you use inverse operation
meaning opposite signs
subtract -13 from 13 cross it out
subtract 13 from 9
you get 1/2x=-4
divide 1/2 on both sides
-4 divided by 1/2 =-8
I think i got the answer but a second opinion would be greatly appreciated!

Answers
Answer:
Your answer would be B: 30 ft squared
Step-by-step explanation:
Find the area of the circle: 5.5 (radius) multiply it by itself then multiply that by 3.14 which gets you 94.985. Now find the area of the square which is 8*8 = 64. Subtract 64 from 94.985 and your answer will be 30.985. The questions asks for the approximate (estimate), so the closest one would be 30 ft squared
The one-to-one functions g and h are defined as follows.g(x) = -2x-13h=(-7 -2) (8)12I
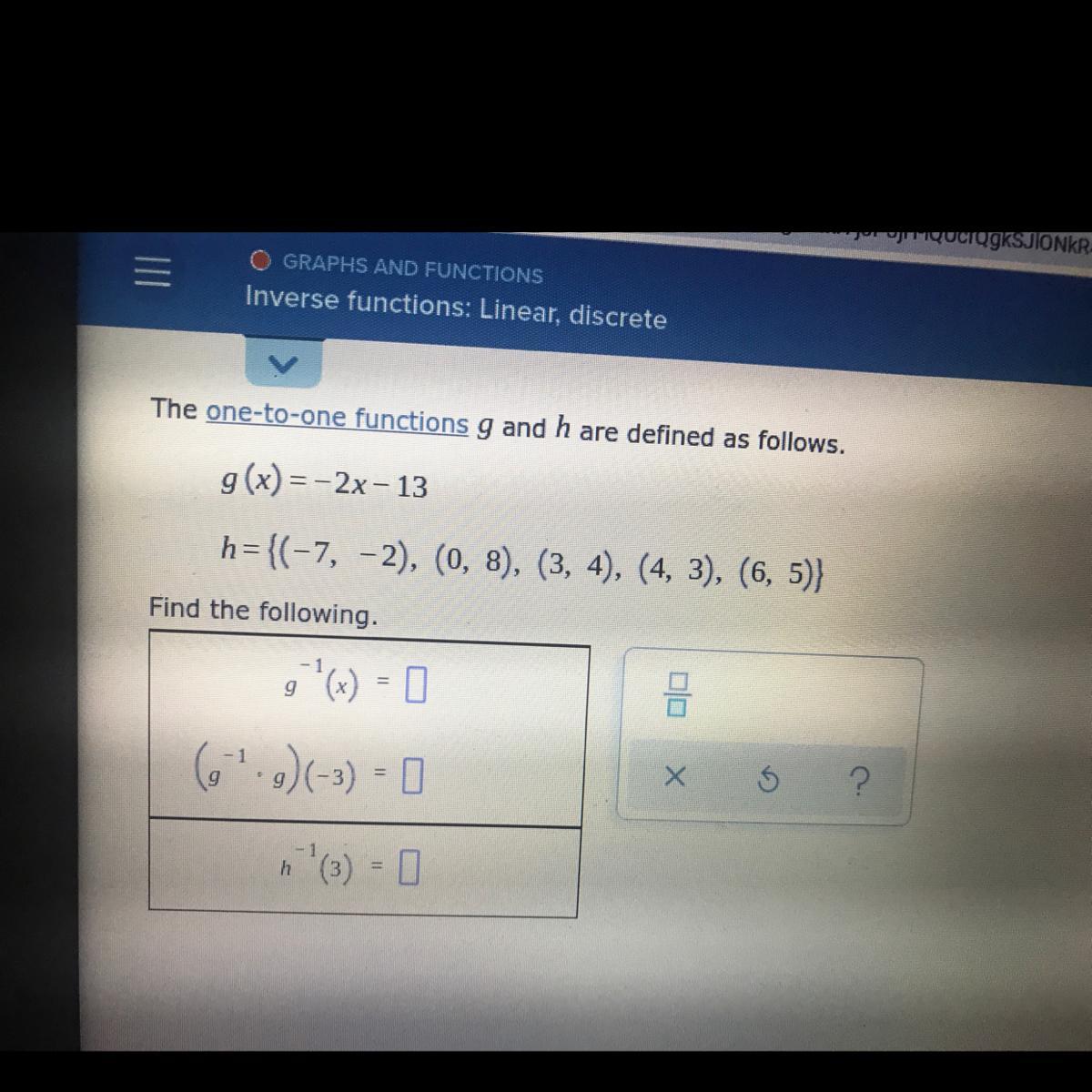
Answers
We have to remember that in one-to-one functions each element of the domain maps to a different element in the range.
When we have a bijection we have that each element in the set A, for example, corresponds to exactly one element of B, and vice versa.
When we have a bijection, we also have an inverse function.
Then, we have that:
\(g(x)=-2x-13\)To find the inverse, we have to interchange the variables:
\(y=-2x-13\)Now, we have:
\(x=-2y-13\)And we need to solve for y:
1. Add 13 to both sides of the equation:
\(x+13=-2y-13+13\Rightarrow x+13=-2y\)2. Divide both sides by -2:
\(\frac{(x+13)}{-2}=\frac{-2y}{-2}\Rightarrow-\frac{(x+13)}{2}=y\)Then, we have that:
\(g^{-1}(x)=-\frac{(x+13)}{2}\)We can check this if we make a composition between the two functions (then we will get x as a result).
\((g^{-1}\circ g)=g^{-1}(g(x))=-\frac{((-2x-13)+13)_{}}{2}=-\frac{(-2x)}{2}=\frac{2x}{2}=x\)Then, we have that the result for this composition is equal to x. Thus:
\((g^{-1}\circ g)(-3)=-3^{}\)We also have that:
We have that h(4) = 3, then h^(-1)(3) = 4 or
\(h(4)=3\Rightarrow h^{-1}(3)=4\)In summary, we have:
\(g^{-1}(x)=-\frac{(x+13)}{2}\)\((g^{-1}\circ g)(-3)=-3\)\(h^{-1}(3)=4\)

NEED ASAP
What is the product?
а-3
11
5
15а а-3
о
о
Cul —
за
о за
O3

Answers
Answer:
1/3a
Step-by-step explanation:
\( \frac{(a - 3)}{15a} \times \frac{5}{(a - 3)} = \frac{5}{15a} = \frac{1}{3a} \)
how to find the scale factor of something
Answers
Answer:
To find the scale factor, locate two corresponding sides, one on each figure. Write the ratio of one length to the other to find the scale factor from one figure to the other. In this example, the scale factor from the blue figure to the red figure is 1.6 : 3.2, or 1 : 2.
Step-by-step explanation:
Please help me with this

Answers
Answer:
\(y=-\frac{5}{2}x-16\)
Step-by-step explanation:
Slope intercept form is a way of expressing a line in the format;
\(y=mx+b\)
Where (m) is the slope of the line, and (b) is the y-intercept. One can solve for (b) by substituting in a point on the line and using inverse operations to solve.
\(y=mx+b\\\\m=-\frac{5}{2}\\\\y=-\frac{5}{2}x+b\)
Substitute in point (-6, -1)
\(-1=-\frac{5}{2}(-6)+b\\\\-1=15+b\\\\-15\\\\-16=b\)
\(y=-\frac{5}{2}x-16\)
Divide (6.3 × 103) by (1.8 × 105) giving your answer in Scientific Notation.
Answers
Answer:
(6.3*10³) ÷ (1.8*10⁵)
6.3*10³ = 0.063*10⁵
then:
(6,3*10³) ÷ (1.8*10⁵) = (0.063*10⁵) ÷ (1.8*10⁵)
= 0.063/1.8
= 0.035
0.035 = 3.5 *10⁻² = 35*10⁻³
HELP
find the a,b,c of this table

Answers
Answer:
a = b = 1 , c = - 8
Step-by-step explanation:
ax² + bx + c = y
( - 5 )² a - 5b + c = 12
c = - 8
3² a + 3b + c = 4
25a - 5b - 8 = 12 ⇔ 25a - 5b = 20 ⇔ 5a - b = 4 ........ (1)
9a + 3b - 8 = 4 ⇔ 9a + 3b = 12 ⇔ 3a + b = 4 .......... (2)
(1) + (2)
8a = 8 ; a = 1
b = 1
y = x² + x - 8
what is the value of 76 + 12/3
Answers
Answer:
80
hope this helps
have a good day :)
Step-by-step explanation:
Constant of Variation
State the relationship between the graphs of f(x) and g(x)
f(x) = 1/x², g(x) 1/x⁴
a. g is closer to the y-axis, and f is closer to the x-axis.
b. g is symmetric about the y-axis, and f is symmetric about the origin.
c. g is symmetric about the y-axis, and f is symmetric about the x-axis.
d. g is closer to the axis, and f is closer to the y-axis.
Please select the best answer from the choices provided
Answers
Answer:
D. G is closer to the axis, and f is closer to the y-axis.
Step-by-step explanation:
I calculated it logically
an academic department has just completed voting by secret ballot for a department head. the ballot box contains four slips with votes for candidate a and three slips with votes for candidate (a) List all possible outcomes. This answer has not been graded yet. (b) Suppose a running tally is kept as slips are removed.
Answers
Therefore , the solution of the given problem of probability comes out to be AAAABBB (4 ballots for candidate A, 3 votes for candidate B) (4 votes for candidate A, 3 votes for candidate B)
What is probability?The primary objective of statistical inference, a branch of mathematics, is to determine the chance that a claim is true or that a specific event will occur. Chance can be represented by any number between 0 and 1, in which 1 typically represents certainty and 0 typically represents possibility. A probability diagram shows the chance that a specific event will occur.
Here,
(a) The voting box contains a total of seven slips, four of which are for candidate A and three for candidate B. Thus, there are 35 events that can occur from 7 choose 4 (or 7 choose 3) options.
Each vote can be represented by a letter, with A standing for a vote for candidate A and B for candidate B, so that all outcomes can be listed. These are the potential results:
AAAA
AAAB
AABA
ABAA
BAAA
AABB
ABAB
BABA
BBAA
ABBB
BABB
BBAB
BBBA
(b)
For instance, the following results could occur if the slips were removed in the following order:
A (1 vote for contender A) (1 vote for candidate A)
AA (2 ballots for candidate A) (2 votes for candidate A)
AAB (2 ballots for candidate A, 1 vote for candidate B) (2 votes for candidate A, 1 vote for candidate B)
AAAB (3 ballots for candidate A, 1 vote for candidate B) (3 votes for candidate A, 1 vote for candidate B)
AAAAB (4 ballots for candidate A, 1 vote for candidate B) (4 votes for candidate A, 1 vote for candidate B)
AAAABB (4 ballots for candidate A, 2 votes for candidate B) (4 votes for candidate A, 2 votes for candidate B)
AAAABBB (4 ballots for candidate A, 3 votes for candidate B) (4 votes for candidate A, 3 votes for candidate B)
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ4