.a. Find the LCM of the 45 and 70
Answers
Answer:
630.
Find the Prime factorization of 45, 3 x 3 x 5
Find the prime factorization of 70, 2 x 5 x7
Multiply each factor the greater number of times it occurs.
You get 630.
LCM of 45 and 70 :
= 45 ÷ 5 , 70 ÷ 5 ( Both the numbers are being divided by 5 ; which is their smallest common factor )
= 14 , 9
= 14 ÷ 14 , 9 ( We are dividing 14 by 14 as both 9 and 14 dont have have a common factor )
= 1 , 9
= 1 , 9 ÷ 3 ( 9 is being divided by 3 )
= 1 , 3
= 1 , 3 ÷ 3 ( 3 is being divided by 3 )
= 1 , 1
LCM of 45 and 70 = 5 × 14 × 3 × 3
LCM of 45 and 70 = 630
Therefore , the LCM of the 45 and 70 = 630 .
Related Questions
omar has four times as many apples as bananas. He has 30 pieces of fruit in all. If a represents the number of apples and b represents the number of bananas , how many of each fruit does omar have?
Answers
Answer:
Omar would have 24 apples and 6 bananas
Step-by-step explanation:
We know that Omar has 4 times as many apples as bananas., which means a is the number of apples and b is the number of bananas.
a=4b
We also know that Omar has 30 fruits in total:
a+b=30
So we have two equations here. We solve them by substituting for a in the second equation with a=4b from equation 1 as shown:
a=b=30
4b+b=30
5b=30
b=6
Omar has 6 bananas. Great!
Now we substitute for apples. We already know that Omar has 6 bananas now, so all we have to do is:
a=4(6)
a=24
Omar has 24 apples.
So Omar has 6 bananas, and 24 apples! Hope this helps! :)
Solve it 21.452÷0.62
Answers
Answer:
34.6
Step-by-step explanation:
1 Find x if:
d) 4:3=x:21
Answers
Answer:
Step-by-step explanation: So, you have to find a number that can be multiplied both by 4 and 3 to get x and 21. So x is 28, 4:3 = 28:21, you can multiply both by 7.
Write the expression in standard form a+bi: (8-i)/(2+i)
Answers
Answer:
The expression (8-i)/(2+i) in standard form is, 3 - 2i
Step-by-step explanation:
The expression is,
(8-i)/(2+i)
writing in standard form,
\((8-i)/(2+i)\\\)
Multiplying and dividing by 2+i,
\(((8-i)/(2+i))(2-i)/(2-i)\\(8-i)(2-i)/((2+i)(2-i))\\(16-8i-2i-1)/(4-2i+2i+1)\\(15-10i)/5\\5(3-2i)/5\\=3-2i\)
Hence we get, in standard form, 3 - 2i
The expression (8-i)/(2+i) in standard form a+bi is (15 - 10i) / (3 + 4i).
To write the expression (8-i)/(2+i) in standard form a+bi, we need to eliminate the imaginary denominator. We can do this by multiplying the numerator and denominator by the conjugate of the denominator.
The conjugate of 2+i is 2-i. So, we multiply the numerator and denominator by 2-i:
(8-i)/(2+i) * (2-i)/(2-i)
Using the distributive property, we can expand the numerator and denominator:
(8(2) + 8(-i) - i(2) - i(-i)) / (2(2) + 2(i) + i(2) + i(i))
Simplifying further:
(16 - 8i - 2i + i^2) / (4 + 2i + 2i + i^2)
Since i^2 is equal to -1, we can substitute -1 for i^2:
(16 - 8i - 2i + (-1)) / (4 + 2i + 2i + (-1))
Combining like terms:
(15 - 10i) / (3 + 4i)
Therefore, the expression (8-i)/(2+i) in standard form a+bi is (15 - 10i) / (3 + 4i).
Learn more:About complex numbers here:
https://brainly.com/question/20566728
#SPJ11
Which of the following triangles are right triangles? Check all that apply. A. A triangle with side lengths 6 inches, 8 inches, 10 inches B. A triangle with side lengths 8, 15, 17 • C. A triangle with side lengths 4, 5, 6 D. A triangle with side lengths 5, 12, 13
Answers
As per the Pythagorean theorem, the right triangles are A triangle with side lengths 6 inches, 8 inches, 10 inches, A triangle with side lengths 8, 15, 17 and A triangle with side lengths 5, 12, 13 (option A, B and D)
Let's consider the four triangles given in the problem:
A. A triangle with side lengths 6 inches, 8 inches, 10 inches B. A triangle with side lengths 8, 15, 17 C. A triangle with side lengths 4, 5, 6 D. A triangle with side lengths 5, 12, 13
To determine whether each triangle is a right triangle, we need to apply the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
For triangle A, we have:
6² + 8² = 10² 36 + 64 = 100 100 = 100
Since the equation is true, we know that triangle A is a right triangle.
For triangle B, we have:
8² + 15² = 17² 64 + 225 = 289 289 = 289
Again, the equation is true, so triangle B is also a right triangle.
For triangle C, we have:
4² + 5² = 6² 16 + 25 = 36 41 ≠ 36
The equation is not true, so triangle C is not a right triangle.
Finally, for triangle D, we have:
5² + 12² = 13² 25 + 144 = 169 169 = 169
Once again, the equation is true, so triangle D is a right triangle.
To know more about triangle here
https://brainly.com/question/8587906
#SPJ1
The triangles are similar. Find the value of x. Show all work

Answers
#7b) Factor (3x-2)-3(3x-2) 40 Substitute y= (3x-2) [4] (7 Marks)
Answers
To factor the expression (3x-2)-3(3x-2), we factored out the common factor of (3x-2) to get -2(3x-2). To substitute y = (3x-2) into this expression, we rewrote it as -2y, which is the same as the original expression but with y replacing (3x-2).
For the expression (3x-2)-3(3x-2), we can factor out the common factor of (3x-2) to get:
(3x-2) - 3(3x-2) = (3x-2)(1-3) = -2(3x-2)
Therefore, -2(3x-2) is the factored form of the expression (3x-2)-3(3x-2).
To substitute y = (3x-2) into this expression, we can rewrite it as:
-2(3x-2) = -2y
This is the same as the original expression, but with y replacing (3x-2).
To know more about factors, visit:
brainly.com/question/14452738
#SPJ11
If you left $25.00 on your table for a $21.50 meal, what was the percent of the tip?
Answers
Answer: 3.5% with a 3.50 Tip
Reason: 25.00 - 21.50 = 3.50
Please help me asap.

Answers
Answer:
B
D
A
C
Step-by-step explanation:
Whatever is listed 2nd in the parentheses, do that function first. Then take that result & do the function listed first.
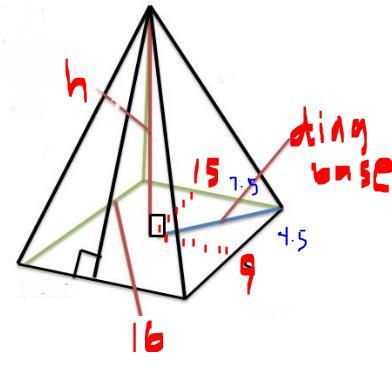
OABCD is a pyramid with a rectangular base of sides 15cm by 9cm.Given that the slant height OQ is 16cm find its
i)height
ii)volume
Answers
Hello! Your answer is below... Remember : h = height and v = volume
Answer:
H = 15.35 cm
V = 690.75 m^
Step-by-step explanation:
(H= height, V = volume, ^= square, √ = square root )
1. divide 9/2
=4.5 cm
2. use the pythagorean theorem
H=√16^-4.5^
H=15.35
if your looking for volume
1. use the formula for volume of the pyramid which is:
1/3 x base area x height
or
base area x height /3
2. then you substitute
1/3 x (9)(15) x 15.35
or
(9)(15) x 15.35 /3
V= 690.75 m^
Hope it helped u if yes mark me BRAINLIEST!
Tysm!
:)
Answer:
height = h = 13.4 cm
volume = V = 602.8 cm³
Step-by-step explanation:
area of a square base = 15 cm x 9 cm = 135 cm²
slant height of pyramid = 16m
solving height: (see attached image)
first step is to take the diagonal base:
side of base 15 = 15 / 2 = 7.5cm
side of base 9 = 9 / 2 = 4.5m
diagonal base = sqrt ( 7.5² + 4.5²) = 8.75 cm
therefore
height² = slant height² - diagonal base²
h² = 16² - 8.75²
h = 13.4 cm
solving the volume:
V = 1/3 * area of square base * h
V = 1/3 * 135 * 13.4
V = 602.8 cm³
Fwam took a taxi from his house to the airport. The taxi company charged a pick-up fee of $3.80 plus $2.25 per mile. The total fare was $33.05, not including the tip.
Answers
The linear equation that represents this situation is given by 3.80+2.25m=33.05. the number of miles travelled is approximately 13.89 miles.
The equation for a linear equation in one variable is written as ax+b = 0, where a and b are two integers, and x is a variable. This equation has only one solution.
Here it is given that the total fare is $33.05
The base fee for the cab is $3.80
Cost per mile is $2.25
Let the distance from Fwam's house and airport be m miles.
Therefore total cost for m miles=2.25m
Total Cost for the cab ride= 3.80+2.25m
But the total cost is $33.05
Hence:
3.80+2.25m=35.05
or, 2.25m=31.25
or, m=13.88888
or, m≈13.89 miles
Hence the distance from the house to the airport is approximately 13.89 miles , which can be calculated from the linear equation: 3.80+2.25m=35.05.
Disclaimer: the complete question is :
Fwam took a taxi from his house to the airport. The taxi company charged a pick-up fee of $3.80 plus $2.25 per mile. The total fare was $33.05, not including the tip. Write and solve an linear equation which can be used to determine m, the number of miles in the taxi ride.
To learn more about Linear equations visit:
https://brainly.com/question/13738061
#SPJ9
two numbers are in the ratio 5:3.if they deffer by 18,what are the numbers?
Answers
Answer:
let common ratio between them be x
So, 5x,3x
5x-3x=18
2x=18
2x/2=18/2
x=9
Step-by-step explanation:
I hope it helps you☺️
If yes, do mark my answer as brainliest
Order these numbers from least to greatest.
2
12/5
2.47
square root of 3
Answers
Answer:
square root, 2,12/5,2.47
Step-by-step explanation:
exercise 1: solve the recurrence relation for the initial condition given. a) an = -3 an-1; a0 = 2
Answers
The recurrence relation for the initial condition given is an = (-3)n (2)
An equation that depicts a sequence based on a rule is called a recurrence relation. Finding the following term, which is contingent upon the preceding term, is made easier. (previous term).
We have the recurrence relation:
an = -3 an-1
Using the above recurrence relation, we can write:
a1 = -3 a0
a2 = -3 a1 = 9 a0
a3 = -3 a2 = -27 a0
a4 = -3 a3 = 81 a0
and so on.
So we can observe that:
an = (-3)n a0
Using the initial condition a0 = 2, we have:
an = (-3)n (2)
The recurrence relation a = -3 an-1 with starting condition a0 = 2 has the following solution: an = (-3)n (2)
Learn more about recurrence relation at https://brainly.com/question/28096566
#SPJ11
Describe in words the surface whose equation is given. (Assume that r is not negative.) θ = π/4
-the plane y = −z where y is not negative
-the plane y = z where y and z are not negative
-the plane y = x where x and y are not negative
-the plane y = −x where y is not negative
-the plane x = z where x and y are not negative
Answers
It illustrates a line equation in the XY plane whose equation is represented by x=y when x and y really aren't negative.
What is an equation?Using the equal symbol (=) to indicate equivalence, a mathematical equation is a formula that joins two statements. An equation in algebra is a statement of mathematics proving the equality of two mathematical equations. In the formula 3x + 5 = 14, for example, the equal sign places the variables 3x + 5 & 14 apart. The relationship between two words on either side of such a letter is described by a mathematical formula. A single variable, which also serves as the symbol, is frequently present. like in 2x - 4 Equals 2, for instance.
The line passing thru the origins and having an equal tangent is known as an equation of the form =. A line's equation is, in general, an equation with the formula = °.
To know more about equation visit:
brainly.com/question/649785
#SPJ4
5/If AB is 12, what is the
length of A' B'?

Answers
Answer:
8
Step-by-step explanation:
Corresponding sides of similar triangles are proportional, so:
\(\frac{A'B'}{12}=\frac{4}{6} \implies A'B'=8\)
If
\[x^2 - 7x + c = (x + a)^2\]for some constants $a$ and $c,$ then find $c.$
Answers
Answer:
Step-by-step explanation:
\(x^{2} -7x+c=(x+a)^{2}\)
\(x^{2} -7x+c=x^{2} +2ax+a^{2}\)
\(-7x=2ax\\a=-7/2\)
\(a^{2} =c\\c=(-7/2)^{2} =49/4\)
at which point on the given curve is the tangent line parallel to the line 5x-y=5 y=4 2e^x-5x
(x,y) = (__ , __)
Answers
The point on the given curve is the tangent line parallel to the line 5x-y=5 y=4 2e^x-5x is (x,y) = ((ln(85/32), -2ln(85/32))
To find the point on the given curve where the tangent line is parallel to the line 5x - y = 5, we need to find the slope of the line 5x - y = 5 and then find the point on the curve where the derivative has the same slope.
The line 5x - y = 5 can be rewritten as y = 5x - 5, which is in the form y = mx + b, where m is the slope of the line. Therefore, the slope of the line is 5.
Now, we need to find the point on the curve where the derivative has the same slope. The given curve is y = 4(2e^x - 5x). To find the slope of the tangent line at a point (x,y) on the curve, we need to find the derivative of y with respect to x:
y = 4(2e^x - 5x)
y' = 4(2e^x - 5)
To find the point where the tangent line has the same slope as the line 5x - y = 5, we need to solve the equation:
y' = 5
4(2e^x - 5) = 5
8e^x - 20 = 5/4
8e^x = 85/4
e^x = 85/32
x = ln(85/32)
Now, we can find the corresponding value of y on the curve by substituting x = ln(85/32) into the equation for the curve:
y = 4(2e^x - 5x) = 4(2(85/32) - 5ln(85/32)) = -2ln(85/32)
Therefore, the point on the curve where the tangent line is parallel to the line 5x - y = 5 is (ln(85/32), -2ln(85/32)).
To know more about tangent line:
https://brainly.com/question/28385264
#SPJ4
Find the transfer function, 3()/()
2. Find the transfer function, \( X_{3}(s) / F(s) \).
Answers
The transfer function 3(s)/s using the following procedure.
Step 1: Start with the equation Y(s) = (3/s)X(s) where Y(s) and X(s) are the Laplace transforms of the output and input signals, respectively.
Step 2: Rewrite the equation to solve for X(s)/Y(s):X(s)/Y(s) = s/3
Step 3: The transfer function is X(s)/Y(s), so the transfer function for 3(s)/s is s/3.
To find the transfer function X3(s)/F(s), follow these steps.
Step 1: Start with the equation X3(s) = (1/s^2)F(s) where X3(s) and F(s) are the Laplace transforms of the output and input signals, respectively.
Step 2: Rewrite the equation to solve for X3(s)/F(s):X3(s)/F(s) = 1/s^2
Step 3: The transfer function is X3(s)/F(s), so the transfer function for X3(s)/F(s) is 1/s^2.
To know more about transfer function visit:
brainly.com/question/33196132
#SPJ11
A line passes through (2, –1) and (8, 4).Write an equation for the line in point-slope form.
Rewrite the equation in standard form using integers.
y – 2 = 5/6 (x + 1); –5x + 6y = 17
y + 1 = 5/6 (x – 2); –5x + 6y = –16
y – 1 = 5/6 (x – 2); –5x + 6y = 16
y + 1 = 5/6 (x + 2); –5x + 6y = –16
Answers
The equation in point slope form and standard form are as follows:
y + 1 = 5 / 6(x - 2)- 5x + 6y = - 16How to write equation in point slope form and standard form?The line passes through (2, -1) and (8, 4). The equation of the line in point slope form and standard form can be represented as follows;
Therefore, in point slope form,
y - y₁ = m(x - x₁)
where
m = slopeTherefore,
slope = m = 4 + 1 / 8 - 2
m = 5 / 6
Hence, using (2, -1)
y + 1 = 5 / 6(x - 2)
In standard form,
y + 1 = 5 / 6 x - 10 / 6
y - 5 / 6 x = - 10 / 6 - 1
y - 5 / 6 x = - 8 / 3
multiply through by 6
6y - 5x = - 16
Therefore,
- 5x + 6y = - 16
learn more on equation here: https://brainly.com/question/29041142
#SPJ1
the rate of college enrollment immediately after high school completion was 67
Answers
The statement " Rate of college enrollment immediately after completing high school was 67% by 1997" is an example of (a) Descriptive Statistics.
The Descriptive statistics involves the use of measures, such as averages, proportions, and frequencies, to summarize and describe the main features of a set of data.
In this statement, the rate of 67% is a summary statistic that describes the proportion of high school graduates who enrolled in college immediately after completing high school in 1997.
Whereas; the inferential statistics involves making inferences or predictions about a population based on a sample of data.
The statement provides a summary statistic for the rate of college enrollment for a specific year, 1997, but it does not provide any inferences or predictions about the rate of college enrollment for other years or other populations , so it denoted a Descriptive Statistics .
The given question is incomplete , the complete question is
What type of Statistics does the statement "the rate of college enrollment immediately after high school completion was 67" represents ?
(a) Descriptive
(b) Inferential
Learn more about Descriptive Statistics here
https://brainly.com/question/29487303
#SPJ4
Abdulbaasit would like to buy a new car that costs $ 30000. The dealership offers to finance the car at 2.4% compounded monthly for 5 years with monthly payments. Instead, Abdulbaasit could get a 5-year loan from his bank at 5.4% compounded monthly and the dealer will reduce the selling price by $3000
when Abdulbaasit pays immediately in cash. Which is the best way to buy a car?
Answers
The best way for Abdulbaasit to buy the car would be to opt for the bank loan with the cash discount, as it offers a lower monthly payment and immediate cost savings.
To determine the best way to buy a car, we need to compare the financing options provided by the dealership and the bank. Let's evaluate both scenarios:
1. Financing at the dealership:
- Car price: $30,000
- Interest rate: 2.4% per year, compounded monthly
- Loan term: 5 years (60 months)
Using the provided interest rate and loan term, we can calculate the monthly payment using the formula for monthly loan payments:
Monthly interest rate = \((1 + 0.024)^(1/12)\) - 1 = 0.001979
Loan amount = Car price = $30,000
Monthly payment = Loan amount * (Monthly interest rate) / (1 - (1 + Monthly interest rate)^(-Loan term))
Plugging in the values:
Monthly payment = $30,000 * 0.001979 /\((1 - (1 + 0.001979)^(-60)) =\)$535.01 (approximately)
2. Bank loan with a cash discount:
- Car price with the $3,000 cash discount: $30,000 - $3,000 = $27,000
- Interest rate: 5.4% per year, compounded monthly
- Loan term: 5 years (60 months)
Using the provided interest rate and loan term, we can calculate the monthly payment using the same formula as above:
Monthly interest rate = (1 + 0.054)^(1/12) - 1 = 0.004373
Loan amount = Car price with cash discount = $27,000
Monthly payment = $27,000 * 0.004373 / (1 - (1 + 0.004373)^(-60)) = $514.10 (approximately)
Comparing the two options, we can see that the bank loan with the cash discount offers a lower monthly payment of approximately $514.10, compared to the dealership financing with a monthly payment of approximately $535.01. Additionally, with the bank loan option, Abdulbaasit can pay immediately in cash and save $3,000 on the car purchase.
Therefore, the best way for Abdulbaasit to buy the car would be to opt for the bank loan with the cash discount, as it offers a lower monthly payment and immediate cost savings.
Learn more about bank loan here:
https://brainly.com/question/29032004
#SPJ11
What is the difference between a parameter and a statistic example?
Answers
Evaluate (10 – 4i) ÷ (5 + i)
Answers
Answer:
the answer would be 23/13 - 15/13i
Step-by-step explanation:
The result of the complex expression (10 – 4i) ÷ (5 + i) is \(\frac{23}{13} - i\frac{15}{13}\) .
Given, complex expression (10 – 4i) ÷ (5 + i)
Complex roots: When the roots are complex in nature then they appear in complex conjugate pair.
Complex roots: a ± ib
Complex number pair : a ± ib
i = iota(imaginary number)
a = real part
b = imaginary part
Value of iota :
\(i = \sqrt{-1}\\ i^2 = -1\)
Complex expression : (10 – 4i) ÷ (5 + i)
Apply rationalization,
Use formula \((a^2 - b^2) = (a+b)(a-b)\).
\(\frac{ (10 - 4i) }{(5 + i)} \times \frac{5-i}{5-i} \\\\= \frac{(10 - 4i) \times (5-i) }{(5+i)(5-i)} \\\\=\frac{50 -30i -4}{5^2 - i^2}\\ \\= \frac{46 - 30i}{25 +1 } \\\\= \frac{46 - 30i}{26} \\\\\)
\(= \frac{23}{13} - i\frac{15}{13}\)
The real part is positive and imaginary part is negative.
Know more about complex number system, here:
https://brainly.com/question/13880878
#SPJ3
f(x, m, s) = 1 √278² exp (-2/2 (x-m) ²) 28² Write a function in the form of gauss(x, m=0, s=1) for computing the Gaussian density. Compute the Gaussian density for the following cases. (a) x=0, m=0, s-1. Give the name of question5a (b) x-2, m=0, s-1. Give the name of question5b (c) x-0, m-2, s-1. Give the name of question5e (d) x=0, m=2, s=2. Give the name of question5d (e) x=3, m-3, s-3.
Answers
Compute the Gaussian density for the following cases. (a) x=0, m=0, s-1. Give the name of question5a (b) x-2, m=0, s-1. The value of the account on January 1, 2021, would be $2,331.57.
To calculate the value of the account on January 1, 2021, we need to consider the compounding interest for each year.
First, we calculate the value of the initial deposit after three years (12 quarters) using the formula for compound interest:
Principal = $1,000
Rate of interest per period = 8% / 4 = 2% per quarter
Number of periods = 12 quarters
Value after three years = Principal * (1 + Rate of interest per period)^(Number of periods)
= $1,000 * (1 + 0.02)^12
≈ $1,166.41
Next, we calculate the value of the additional $1,000 deposit made on January 1, 2019, after two years (8 quarters):
Principal = $1,000
Rate of interest per period = 2% per quarter
Number of periods = 8 quarters
Value after two years = Principal * (1 + Rate of interest per period)^(Number of periods)
= $1,000 * (1 + 0.02)^8
≈ $1,165.16
Finally, we add the two values to find the total value of the account on January 1, 2021:
Total value = Value after three years + Value after two years
≈ $1,166.41 + $1,165.16
≈ $2,331.57
Therefore, the value of the account on January 1, 2021, is approximately $2,331.57.
Learn more about value here: brainly.com/question/9796766
#SPJ11
Which postulate or theorem proves that these two triangles are
congruent?

Answers
Answer:
AAS Congruence Theorem
Step-by-step explanation:
I see 2 angles of one triangle shown to be congruent to 2 angles of the other triangle. After the two angles, there is a side in common to both triangles which is congruent to itself. That makes angle-angle-side.
Answer: AAS Congruent Theorem
What is 1 x 10 to the power of -3 in written form
Answers
Answer:
0.001 or 1/1000
Step-by-step explanation:
1 x 10^-3
move decimal forward 3 times to make it a small number.
1. -> 0.001
Please help me find X

Answers
The value of x in the figure is 50 degrees.
What is Circle?A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre.
A tangent line is perpendicular to the radius of the circle.
The angle at which tangent touches the circle has right angle.
There are two right angles.
We know that the sum of interior angles of a quadrilateral is 360 degrees.
130+90+90+x=360
310+x=360
Substitute 310 from both sides
x=50 degrees
Hence, the value of x in the figure is 50 degrees.
To learn more on Circles click:
https://brainly.com/question/11833983
#SPJ1
Brenton’s weekly pay, P(h) , in dollars, is a function of the number of hours he works, h. He gets paid $20 per hour for the first 40 hours he works in a week. For any hours above that, he is paid overtime at $30 per hour. He is not permitted to work more than 60 hours in a week.
Answers
let x be a uniformly distributed random variable on [0,1] then x divides [0,1] into the subintervals [0,x] and [x,1]. by symmetry
Answers
When x is a uniformly distributed random variable on [0,1], it divides the interval [0,1] into two subintervals: [0,x] and [x,1]. This division exhibits symmetry, as explained in the following paragraphs.
Consider a uniformly distributed random variable x on the interval [0,1]. The probability density function of x is constant within this interval. When x takes a particular value, it acts as a dividing point that splits [0,1] into two subintervals.
The first subinterval, [0,x], represents all the values less than or equal to x. Since x is randomly distributed, any value within [0,1] is equally likely to be chosen. Therefore, the probability of x falling within the subinterval [0,x] is equal to the length of [0,x] divided by the length of [0,1]. This probability is simply x.
By symmetry, the second subinterval, [x,1], represents all the values greater than x. The probability of x falling within the subinterval [x,1] can be calculated as the length of [x,1] divided by the length of [0,1], which is equal to 1 - x.
The symmetry arises because the probability of x falling within [0,x] is the same as the probability of x falling within [x,1]. This symmetry is a consequence of the uniform distribution of x on the interval [0,1].
Learn more about probability density function :
https://brainly.com/question/31039386
#SPJ11