a drag racer has two parachutes, a main and a backup, that are designed to bring the vehicle to a stop after the end of a run. suppose that the main chute deploys with probability 0.96, and that if the main fails to deploy, the backup deploys with probability 0.95.a. What is the probability that one of the twoparachutes deploys?b. What is the probability that the backup parachutesdeploys?
Answers
(a) The probability that one of the two parachutes deploys is 0.998.
(b) The probability that the backup parachutes deploys is 0.038.
a. The probability that one of the two parachutes deploys is the sum of the probability that the main chute deploys and the probability that the backup chute deploys, minus the probability that both chutes deploy.
This can be represented by the formula:
P(one of the two parachutes deploys) = P(main chute deploys) + P(backup chute deploys) - P(both chutes deploy)
P(one of the two parachutes deploys) = 0.96 + 0.95 - (0.96)(0.95)
P(one of the two parachutes deploys) = 1.91 - 0.912
P(one of the two parachutes deploys) = 0.998
Therefore, the chance that one of the two parachutes will deploy is 0.998.
b. The probability that the backup parachute deploys is the probability that the main chute fails to deploy multiplied by the probability that the backup chute deploys.
This can be represented by the formula:
P(backup chute deploys) = P(main chute fails to deploy) x P(backup chute deploys)
P(backup chute deploys) = (1 - 0.96)(0.95)
P(backup chute deploys) = 0.04(0.95)
P(backup chute deploys) = 0.038
Therefore, the chance that the backup parachute will deploy is 0.038.
Learn more about probability here: https://brainly.com/question/24756209.
#SPJ11
Related Questions
determine the values of the missing entries. reduce all fractions to the lowest terms
9x-6y= 18

Answers
By evaluating the given linear relation, we conclude that the complete table is:
x: 2, 0, 1, 14/3
y: 0, -3, -3/2, 4
How to determine the values of the missing entries?Here we have the linear relation:
9x - 6y = 18
And we want to complete the given table, to do so, we just need to evaluate the relation in the given values and with that we can find the missing ones.
For example, the first pair has y = 0.
Evaluating that we get:
9x - 6*0 = 18
9x = 18
x = 18/9 = 2
Then we have the pair (2, 0).
The second has x = 0, replacing that we get:
9*0 - 6*y = 18
y = 18/-6 = -3
So we have the pair (0, -3)
The third has x = 1, replacing that:
9*1 - 6y = 18
-6y = 18 - 9 = 9
y = 9/-6 = -3/2
So we have the pair (1, -3/2)
The last value on the table is y = 4, replacing that:
9x - 6*4 = 18
9x - 24 = 18
9x = 18 + 24 = 42
x = 42/9 = 14/3
Then the complete table is:
x: 2, 0, 1, 14/3
y: 0, -3, -3/2, 4
If you want to learn more about linear relations:
https://brainly.com/question/1884491
#SPJ1
Hey guys I need some help, Ty :)

Answers
Step-by-step explanation:
Download math may that help
Write a system of equations to describe the situation below, solve using any method, and fill in the blanks.Carter and Anna are making presentations for a class project. Carter's slideshow starts with a verbal introduction that is 13 seconds long, and then each slide is left up for 10 seconds. Anna leaves each slide onscreen for 6 seconds, and her introduction lasts 17 seconds. Carter and Anna notice that their presentations have both the same number of slides and the same duration. How long is each presentation? How many slides are in each presentation?
Answers
Given
Carter and Anna are making presentations for a class project.
Carter's slideshow starts with a verbal introduction that is 13 seconds long, and then each slide is left up for 10 seconds.
Anna leaves each slide onscreen for 6 seconds, and her introduction lasts 17 seconds.
Carter and Anna notice that their presentations have both the same number of slides and the same duration.
To find how long is each presentation and how many slides are in each presentation.
Now,
Let x be the time taken for each presentation and y be the number of slides.
Then, the equations are,
\(\begin{gathered} 13+10y=x\text{ \_\_\_\_(1)} \\ 17+6y=x\text{ \_\_\_\_\_(2)} \end{gathered}\)Therefore,
\(\begin{gathered} 13+10y=17+6y \\ 10y-6y=17-13 \\ 4y=4 \\ y=1 \end{gathered}\)Substitute y=1 in (1).
Then,
\(\begin{gathered} 13+10y=x \\ 13+10\times1=x \\ x=13+10 \\ x=23 \end{gathered}\)Hence, the time taken for each presentation is 23 seconds and the number of slides is 1.
2x2 - 4x –9 = 0
Completing the swuare
Answers
Step-by-step explanation:
\((a-b)^2=a^2-2ab+b^2\\\\2x^2-4x-9=0\qquad|\text{add 9 to both sides}\\\\2x^2-4x-9+9=0+9\\\\2x^2-4x=9\qquad|\text{divide both sides by 2}\\\\\dfrac{2x^2}{2}-\dfrac{4x}{2}=\dfrac{9}{2}\\\\x^2-2x=4.5\\\\x^2-2\cdot x\cdot1=4.5\qquad|\text{add}\ 1^2\ \text{to both sides}\\\\x^2-2\cdot x\cdot1+1^2=4.5+1^2\\\\(x-1)^2=5.5\iff x-1=\pm\sqrt{5.5}\qquad|\text{add 1 to both sides}\\\\x=1-\sqrt{5.5}\ \vee\ x=1+\sqrt{5.5}\)
Kevin's bank deducts a service fee from his account every month.
In one year, the bank deducts a total of $90 in fees. Twice each
month, Kevin's paycheck is directly deposited into his account.
The amount of each paycheck is $1,150. Which expression
represents the monthly change in Kevin's bank account?
Answers
The expression that represents the monthly change in Kevin's bank account is $2,300 - $7.50 = $2,292.50
How to find the expressionIn one year, which has 12 months, the bank deducts a total of $90 in fees. To find the monthly change in Kevin's bank account, we need to divide this total by 12:
Monthly service fee = $90 / 12 = $7.50
Kevin's paycheck is deposited twice each month, so his total monthly income from his paychecks is:
Monthly income = 2 * $1,150 = $2,300
Therefore, Kevin's monthly change in his bank account is:
Monthly change = Monthly income - Monthly service fee
Monthly change = $2,300 - $7.50 = $2,292.50
So the expression that represents the monthly change in Kevin's bank account is $2,300 - $7.50 = $2,292.50
Learn more about expression at:https://brainly.com/question/1859113
#SPJ1
If y varies inversely as X and y=16 when X=4,find y when X=32
Answers
\(\qquad \qquad \textit{inverse proportional variation} \\\\ \textit{\underline{y} varies inversely with \underline{x}} ~\hspace{6em} \stackrel{\textit{constant of variation}}{y=\cfrac{\stackrel{\downarrow }{k}}{x}~\hfill } \\\\ \textit{\underline{x} varies inversely with }\underline{z^5} ~\hspace{5.5em} \stackrel{\textit{constant of variation}}{x=\cfrac{\stackrel{\downarrow }{k}}{z^5}~\hfill } \\\\[-0.35em] ~\dotfill\)
\(\stackrel{\textit{"y" varies inversely with "x"}}{y = \cfrac{k}{x}}\hspace{5em}\textit{we also know that} \begin{cases} x=4\\ y=16 \end{cases} \\\\\\ 16=\cfrac{k}{4}\implies 64 = k\hspace{9em}\boxed{y=\cfrac{64}{x}} \\\\\\ \textit{when x = 32, what's "y"?}\qquad y=\cfrac{64}{32}\implies y=2\)
Find the surface area of the figure.

Answers
Answer:
152 cm²
Step-by-step explanation:
2x5x3=30
2x6x3=36
5x6=30
2x2.5x6=30
2x6=12
(2+5)/2=3.5x2=7x2=14
30+36+30+30+12+14=152
What are 3 antonym words for absolute value. ASAP
Answers
Answer:
Undervalue , overestimate , overvalue , decrimalize
Step-by-step explanation:
Hope this helps
A train running between two stations 50 Km apart arrives on time if it travels at an
average speed of 60 km/h. How late will it be if travels at an average speed of 50 Km/h?
Answers
If the train travels at an average speed of 50 Km/h, it would be late by 10 minutes.
How late will the train be if it travels at an average speed of 50 Km/h?Speed is simply referred to as distance traveled per unit time.
It is expressed as:
Speed = distance / time
Given that the train running between two stations 50 Km apart arrives on time if it travels at an average speed of 60 km/h.
The time taken by the train to travel 50 km at an average speed of 60 km/h can be calculated using the formula:
Speed = distance / time
time = distance / speed
time = 50 km / 60 km/h
time = 5/6 hour
Next, if the train travels at an average speed of 50 km/h, the time taken to cover the same distance of 50 km would be:
Speed = distance / time
time = distance / speed
time = 50 km / 50 km/h
time = 1 hour
Now, the difference in time between the two scenarios would be:
time difference = 1 hour - 5/6 hour
time = 1/6 hour
Convert to minutes
time = 1/6 × 60
time = 10 minutes
Therefore, the train would be late by 10 minutes.
Learn more about speed here: https://brainly.com/question/27571996
#SPJ1
Type the correct answer in box. Use numerals instead of words. THIS IS NOT A TEST.
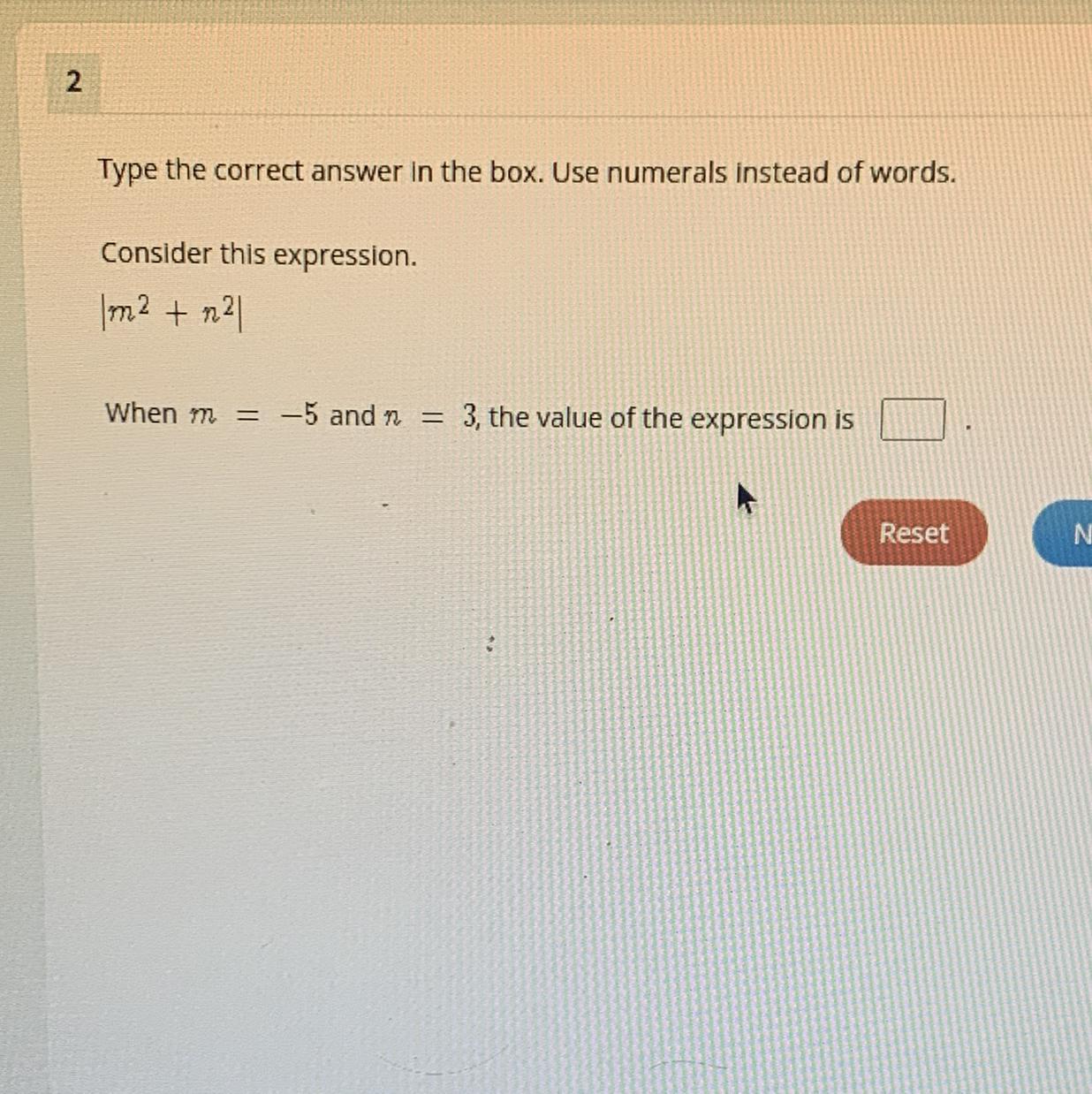
Answers
The expression is,
\(|m^2+n^2|\)Substitute -5 fo m and 3 for n in the expression.
\(\begin{gathered} |(-5)^2+(3)^2|=|25+9| \\ =|34| \\ =34 \end{gathered}\)So answer is 34.
what is da rate to question

Answers
The calculated value of the rate of the graph is 0.8
How to determine the rate of the graphfrom the question, we have the following parameters that can be used in our computation:
The graph
Where, we have
(0, -16) and (20, 0)
The rate of the graph is calculated as
Rate = Change in y/x
using the above as a guide, we have the following:
Rate = (0 + 16)/(20 - 0)
Evaluate
Rate = 0.8
Hence, the rate is 0.8
Read more about slope at
https://brainly.com/question/33472030
#SPJ1
can anyone help me ??? pleassee on both of em

Answers
Answer:
28. B
29. D
30. A
Step-by-step explanation:
28.
2 5/8 yd × 5/6 yd =
= 21/8 × 5/6 yd²
= 105/48 yd²
= 35/16 yd²
= 2 3/16 yd²
Answer: B
29.
2641 becomes 6241.
In 6241, the 6 is in the thousands place.
6 × 1000 = 6000
Answer: D
30.
90 + 7 × (7 - 1) =
Use the correct order of operations.
= 90 + 7 × 6
= 90 + 42
= 132
Answer: A
A geometric sequence h starts at 16 and has a growth factor of 1.75 what are the first 5 terms

Answers
16, 17.75, 19.5, 21.25, 23, 24.75
The required first five-term of the geometric progression is 16, 28, 49, 85.75, 150.06.
Given that,
A geometric sequence h starts at 16 and has a growth factor of 1.75 what are the first 5 terms is to be determined.
Geometric progression is sequence of series whose ratio with adjacent values remains same.
Here,
For the geometric progression,
a = 16
r = 1.75
The required sequence is given as,
1st = a = 16
2nd = ar = 16 (1.75) = 28
3rd = ar² = 16(1.75)² = 49
Similarly,
4th = 85.75
5th = 150.06
Thus, The required first five-term of the geometric progression is 16, 28, 49, 85.75, 150.06.
Learn more about geometric progression here: https://brainly.com/question/4853032
#SPJ5
find sin 2x,cos2x and tan2x,if tanx=-(3)/(4)and x terminates in quadrant IV
Answers
Answer:PLEASE HELP ME
Step-by-step explanation:
here can you guys please help me with this question.
I have been asking help from so many people but no one is nice enough to give it so im hoping that anyone over here can help me. this is the problem
Carl is standing at the base of a zip line which is 400 ft away from the base of the building that is connected to the top of a building. Standing 5.5 ft tall, he looks up to the top of the building at an angle of elevation of 25 degrees. A weight is released and travels down the zip line to his feet. How far did the weight travel? Round to nearest 10th of a foot and do not use units in your answer.
Please show work
You draw one card from a 52-card deck. Then the card is replaced in the deck and the deck is shuffled, and you draw again. Find the probability of drawing a six the first time and a spade the second time
Answers
Answer:
1/4(1/4)=1/16, or 6.25% chance.
Step-by-step explanation:
There are 13 spades in a deck of 52 cards. This is a 13/52, or 1/4 chance of selecting one. As the cards are replaced we just multiply the probabilities of picking a spade.
I hope this helps!
What is the next number in the pattern?

Answers
Answer:
9
Step-by-step explanation:
3 3/4= 3.75.
3.75-2=1.75
1.75+5.5=7.25 or 7 1/4
7.25+1.75=9
If i have 2 apples, how many apples would I have if i divided 2 by 7 ( the number of crates the apples are in)
Answers
Answer:
You can't divide 2 by 7 unless you will round and need a decimal because it will equal 0.28571428571 but if you mean 7 divided by 2 then that would get you 3.5
Step-by-step explanation:
A girl was 6 and sister was 2,the girl is now 24,how old is the sister
Answers
Answer:
20
Step-by-step explanation:
There is 6-2 =4 years between them
24-4 =20
The sister is 20
Answer: 20 years old
Step-by-step explanation: So, we know the girl is 4 years older than the sister...how do we know that? Because...
6 - 2 = 4
She's 4 years older...we know the girl is 24, then the sister must be 20.
24 - 4 - 20...
The sister is 20 years old, I hope this helps
6. Write an expression to represent this situation:
Max has $10. He earns $25.75 for every lawn he mows. Use x for the amount of lawns he mows.
Enter your answer
Answers
Answer:
10 + $25.75x
Step-by-step explanation:
He has 10 dollars to start out with, then you put x to show that we don't know how many lawns he will mow, but that's how much he makes when he does.
Donnez l’intégral de -x+5/(x^2-4x+4)(x+1)
Answers
Answer:
\(\frac{2}{3}\ln(x+1)-\frac{1}{x-2} -\frac{2}{3}\ln(x-2)+C\)
Step-by-step explanation:
Integrate the following expression.
\(\int \frac{-x+5}{(x^2-4x+4)(x+1)}\)
\(\hrulefill\)
In order to integrate this function we are gonna have to use partial fraction decomposition. Start by factoring the the denominator completely.
\(\int \frac{-x+5}{(x^2-4x+4)(x+1)}dx\\\\\Longrightarrow \int \frac{-x+5}{(x-2)^2(x+1)}dx\)
Now we can apply partial fractions. Partial fractions allows us to split up complex fractions, in doing so this will make them easier to integrate.
\(\frac{-x+5}{(x-2)^2(x+1)}=\frac{A}{x+1}+\frac{B}{(x-2)^2}+\frac{C}{x-2}\\\\\Longrightarrow \frac{-x+5}{(x-2)^2(x+1)}=\frac{A}{x+1}+\frac{B}{(x-2)^2}+\frac{C}{x-2} \Big](x-2)^2(x+1)\\\\\Longrightarrow \boxed{-x+5=A(x-2)^2+B(x+1)+C(x-2)(x+1)}\)
Expand the right-hand-side and use the comparison method to find the values of the undetermined coefficients, A, B, and C.
\(-x+5=A(x-2)^2+B(x+1)+C(x-2)(x+1)\\\\\Longrightarrow -x+5=Ax^2-4Ax+4A+Bx+B+Cx^2-Cx-2C\\\\\Longrightarrow \boxed{0x^2-x+5(1)=(A+C)x^2+(-4A+B-C)x+(4A+B-2C)(1)}\)
We can now form a system of equations.
For x^2 terms:
\(A+C=0\)
For x terms:
\(-4A+B-C=-1\)
For #'s:
\(4A+B-2C=5\)
\(\Longrightarrow \left\{\begin{array}{ccc}A+C=0\\-4A+B-C=-1\\4A+B-2C=5\end{array}\right\)
You can use any method of choice to solve the system of equations. I am going to put the system in a matrix and use my calculator to row reduce.
\(\Longrightarrow \left[\begin{array}{ccc}1&0&1\\-4&1&-1\\4&1&-2\end{array}\right] =\left[\begin{array}{c}0\\-1\\5\end{array}\right]\\\\ \\ \ \ \ \Longrightarrow \left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right] =\left[\begin{array}{c}\frac{2}{3} \\1\\-\frac{2}{3}\end{array}\right]\\\\\\\therefore \boxed{A=\frac{2}{3}, \ B=1, \ \text{and} \ C=-\frac{2}{3}}\)
Now we can split up the fraction.
\(\frac{-x+5}{(x-2)^2(x+1)}=\frac{A}{x+1}+\frac{B}{(x-2)^2}+\frac{C}{x-2}\\\\\Longrightarrow \boxed{\frac{-x+5}{(x-2)^2(x+1)}=\frac{\frac{2}{3} }{x+1}+\frac{1}{(x-2)^2}+\frac{-\frac{2}{3}}{x-2}}\)
We can integrate the three fractions separately.
\(\Longrightarrow \int \frac{\frac{2}{3} }{x+1}dx+ \int \frac{1}{(x-2)^2}dx+\int \frac{-\frac{2}{3}}{x-2}dx\\\\\Longrightarrow \boxed{\frac{2}{3}\int \frac{1 }{x+1}dx+ \int \frac{1}{(x-2)^2}dx-\frac{2}{3}\int \frac{1}{x-2}dx}\\\\\)
For the first integral let u=x+1 => du=dx, for the second let v=x-2 => dv=dx, and for the third integral let w=x-2 => dw=dx
\(\Longrightarrow \frac{2}{3} \int \frac{1 }{u}du+ \int \frac{1}{v^2}dv-\frac{2}{3}\int \frac{1}{w}dw\\\\\Longrightarrow \boxed{\frac{2}{3} \int \frac{1 }{u}du+ \int v^{-2}dv-\frac{2}{3}\int \frac{1}{w}dw}\)
Use the rules of integration to integrate.
\(\boxed{\left\begin{array}{ccc}\text{\underline{Natural Log Rule:}}\\\\ \int\frac{1}{x}dx=\ln(x) \end{array}\right} \ \ \boxed{\left\begin{array}{ccc}\text{\underline{Power Rule:}}\\\\ \int x^ndx=\frac{x^{n+1}}{n+1} \end{array}\right}\)
\(\frac{2}{3} \int \frac{1 }{u}du+ \int v^{-2}dv-\frac{2}{3}\int \frac{1}{w}dw\\\\\Longrightarrow \frac{2}{3}\ln(u)-v^{-1}-\frac{2}{3}\ln(w)+C\\\\\Longrightarrow \frac{2}{3}\ln(x+1)-(x-2)^{-1}-\frac{2}{3}\ln(x-2)+C\\\\\Longrightarrow \frac{2}{3}\ln(x+1)-\frac{1}{x-2} -\frac{2}{3}\ln(x-2)+C\\\\\therefore \boxed{\boxed{\int \frac{-x+5}{(x^2-4x+4)(x+1)}=\frac{2}{3}\ln(x+1)-\frac{1}{x-2} -\frac{2}{3}\ln(x-2)+C}}\)
Thus, the given integral is solved where "C" is some arbitrary constant that can be found given an initial condition.
A school supervisor wants to determine the percentage of students that bring their lunch to school. What method would assure random selection of a sample population?
Answers
To assure the random selection of a sample population for determining the percentage of students who bring their lunch to school, a method known as simple random sampling can be employed.
Simple random sampling is a technique that provides each member of the population an equal chance of being selected for the sample. Here's an explanation of how simple random sampling can be implemented in this scenario:
Define the population: The school supervisor needs to clearly define the population of interest, which would be all the students in the school.Assign a unique identifier: Each student should have a unique identifier, such as a student ID number, to differentiate them from one another.Generate a sampling frame: A sampling frame is a list of all the unique identifiers of the students. This could be obtained from the school's records or databases.Determine the sample size: The school supervisor needs to decide on the desired sample size, ensuring it is representative of the population while being practical to manage.Use a random selection method: Employ a random selection method, such as using a random number generator or a random number table, to select the required number of unique identifiers from the sampling frame.Contact selected students: Once the sample has been selected, the chosen students can be contacted to participate in the survey or data collection regarding whether they bring their lunch to school.know more about percentage here:
https://brainly.com/question/24877689
#SPJ8
analyze the diagram below and complete instructions that follow find the value of x in the value of y

Answers
Answer:
The values are \(x=2\sqrt{2}\) and \(y=2\sqrt{6}\).
Step-by-step explanation:
A right triangle is a type of triangle that has one angle that measures 90°.
In a right triangle, the sine of an angle is the length of the opposite side divided by the length of the hypotenuse.
\(\sin(\theta)=\frac{opposite \:site}{hypotenuse}\)
To find the value of x we use the above definition. From the diagram we can see that the angle is 30º and the hypotenuse is \(4\sqrt{2}\). Therefore,
\(\sin(30)=\frac{x}{4\sqrt{2} }\\\\\frac{x}{4\sqrt{2}}=\sin \left(30^{\circ \:}\right)\\\\\frac{8x}{4\sqrt{2}}=8\sin \left(30^{\circ \:}\right)\\\\\sqrt{2}x=4\\\\\frac{\sqrt{2}x}{\sqrt{2}}=\frac{4}{\sqrt{2}}\\\\x=2\sqrt{2}\)
To find the value of y we use the above definition. From the diagram we can see that the angle is 60º and the hypotenuse is \(4\sqrt{2}\). Therefore,
\(\sin(60)=\frac{y}{4\sqrt{2} }\\\\\frac{y}{4\sqrt{2}}=\sin \left(60^{\circ \:}\right)\\\\\frac{8y}{4\sqrt{2}}=8\sin \left(60^{\circ \:}\right)\\\\\sqrt{2}y=4\sqrt{3}\\\\\frac{\sqrt{2}y}{\sqrt{2}}=\frac{4\sqrt{3}}{\sqrt{2}}\\\\y=2\sqrt{6}\)
Answer:
C.
Step-by-step explanation:
trust me its correct on EDGE2021
Henry correctly factored 42? + 52 - 6 as (4% - 3)(₴ + 2)
• He then claimed that the zeros of that quadratic function are located at
*=-=
and r = 2 . Did Henry correctly find the zeros of the function?
O Yes, Henry correctly found the zeros of the function.
O No, the zeros of the function are at x = 4 and =-2
• No, the zeros of the function are at z = - 5 andx = 2.
• No, the zeros of the function are at & = 4 and ≥ = -2
I attached the question and answer choices
Please help

Answers
Answer:
No, the zeros of the function are at x = 3/4 and x = –2
Step-by-step explanation:
the equation
4x² + 5x – 6 = 0
(note: since there is a coefficient of x² we need to multiply it to the last term(6))
4x² + 5x – 24 = 0
the factors are :- 8x and – 3x
4x² + 8x – 3x – 6 = 0
4x( x + 2) –3( x + 2) = 0
( 4x – 3)( x + 2) = 0
the zeros will be
4x – 3 = 0
4x = 3
\(x = \frac{3}{4} \)
x + 2 = 0
x = – 2
the zeros are x= 3/4 or –2
i hope this helps
How many three letter passcodes can you make, where the first letter must be a vowel?
Answers
Answer:
app
and
ack
abc
as.s (my favorite)
add
all
i can make more im just lazy lol have a good day kind sir/madam/person
Lena sells two types of fidget toys. The price for each fidget toy A is x and the price for each Fidget B is y. Write an equation that will let her earn a profit of $3500 if she sells 20 of Fidget A and 60 of Fidget B
Answers
Answer:
3500 = 20x + 60y
Step-by-step explanation:
Its just the answer
Name the Inequalities

Answers
just explain how this is "Reflexive Property" (30 points)!!

Answers
The Reflexive Property is a property of equality that states that anything is equal to itself. This property is true for numbers, shapes, angles, and more.
In the context of geometry, the Reflexive Property of Congruence states that any geometric figure is congruent to itself. This includes angles, segments, triangles, and other polygons.
So, when you see "<J ≅ <J", it's saying that angle J is congruent to angle J, which is an application of the Reflexive Property. In other words, any angle is congruent (equal in measure) to itself.
There are 32 chickens and 12 sheep on a farm. The ratio of sheep to horses is 4:1. Write a ratio expressing the relationship between the chicken and the sheep. Then explain what that ratio means. Determine the number of horses on the farm.
Answers
This means that for every 1 sheep on the farm, there are 0.25 horses. To find the total number of horses, we can multiply the number of sheep by 0.25:
\(12 * 0.25 = 3\)
What is ratio?Ratio refers to the quantitative relationship between two or more quantities, expressing the proportion of one quantity to the other(s). It is typically expressed as a fraction, where the numerator represents one quantity, and the denominator represents the other quantity.
For example, the ratio of the number of boys to the number of girls in a class of 30 students might be expressed as 2:3, which means there are 20 girls and 10 boys in the class. Similarly, the ratio of the length to the width of a rectangle might be expressed as 4:3, indicating that the length is four times greater than the width.
The ratio of sheep to horses is 4:1, which means that for every 4 sheep on the farm, there is 1 horse. We can also say that the total ratio of sheep and horses on the farm is 4+1=5.
To express the relationship between the chickens and the sheep, we need to use the fact that there are 32 chickens and 12 sheep on the farm. We can write this as a ratio:
\(chickens : sheep = 32 : 12\)
We can simplify this ratio by dividing both sides by 4:
\(chickens: sheep = 8: 3\)
This means that for every 8 chickens on the farm, there are 3 sheep.
To determine the number of horses on the farm, we can use the fact that the total ratio of sheep and horses is 5. We know that the ratio of sheep to horses is 4:1, so we can write:
\(sheep : horses = 4 : 1\)
We can simplify this ratio by dividing both sides by 4:
\(sheep : horses = 1 : 0.25\)
This means that for every 1 sheep on the farm, there are 0.25 horses. To find the total number of horses, we can multiply the number of sheep by 0.25:
\(12 * 0.25 = 3\)
To know more about denominator, visit:
https://brainly.com/question/17153086
#SPJ1
Find the derivative of f(x) = negative 9 divided by x at x = -4. (6 points) 4 divided by 9 16 divided by 9 9 divided by 16 9 divided by 4
Answers
Answer:
9/16
Step-by-step explanation:
\(f(x)=-\frac{9}{x}\)
\(f(x)=-9x^{-1}\)
Derivative rule:
\(f(x)=x^{n} \\\)
\(\frac{df}{dx}=nx^{n-1}\)
Here, n=-1, so
\(\frac{df}{dx}=(-9)(-1)x^{-2} =\frac{9}{x^{2} }\)
Evaluating this at x=-4 gives 9/16
Answer:
9/16
Step-by-step explanation:
How can I solve this? Thank you in advance!!
One number is randomly selected from {1, 2, 3, 4, 5, 6, 7, 8, 9}. Find the probability that the selected number is an odd number or a multiple of 3.
Answers
Answer:
The probability that the selected number is an odd number or a multiple of 3 is 6/9, or 2/3. This is because there are 6 numbers that meet the criteria out of the 9 numbers in the set: 1, 3, 5, 7, 9, and 3.