A die is rolled. What is the probability that the result is less than 3?
Answers
Answer:
1/6 if the die is 6 sided
Step-by-step explanation:
it wold have a 1/6 chance to land on 3 if the die is 6 sided
Related Questions
An investor purchased 100 shares of stock in a company for $20 per share. One year later, the investor sold all the shares for $1,950. What is the investor's rate of return?
A. -2.5%
B. -1.6%
C. 2.5%
D. 1.6%
Answers
The investor's rate of return is given as follows:
A. -2.5%.
How to obtain the rate of return?The rate of return is obtained applying the proportions in the context of the problem.
An investor purchased 100 shares of stock in a company for $20 per share, hence the total cost of the purchase was of:
20 x 100 = $2000.
One year later, the investor sold all the shares for $1,950, hence the return was of:
1950 - 2000 = -$50.
Then the rate of return is calculated as follows:
-50/2000 = -2.5%.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
In BINGO, a $5\times5$ card is filled by marking the middle square as WILD and placing 24 other numbers in the remaining 24 squares. Specifically a card is made by placing 5 numbers from the set $1-15$ in the first column, 5 numbers from $16-30$ in the second column, 4 numbers $31-45$ in the third column (skipping the WILD square in the middle), 5 numbers from $46-60$ in the fourth column and 5 numbers from $61-75$ in the last column. One possible BINGO card is: To play BINGO, someone names numbers, chosen at random, and players mark those numbers on their cards. A player wins when he marks 5 in a row, horizontally, vertically, or diagonally. How many distinct possibilities are there for the values in the diagonal going from top left to the bottom right of a BINGO card, in order?
5 16 35 46 75
4 17 34 47 76
3 18 wild 48 73
2 19 32 49 72
1 20 31 50 71
Answers
There are a total of $15^5 = 759,375$ distinct possibilities for the values in the diagonal going from top left to the bottom right of a BINGO card, in order.
To find the number of distinct possibilities for the values in the diagonal going from top left to the bottom right of a BINGO card, we need to consider the range of numbers that can be placed in the diagonal.
In the given BINGO card, the diagonal starts with the number 5 in the top left corner and ends with the number 71 in the bottom right corner. We can see that the numbers in the diagonal follow a pattern:
5, 17, 32, 49, 71
We can analyze this pattern to find the number of distinct possibilities.
- The first number, 5, can be any number from the set $1-15$.
- The second number, 17, can be any number from the set $16-30$.
- The third number, 32, can be any number from the set $31-45$.
- The fourth number, 49, can be any number from the set $46-60$.
- The fifth number, 71, can be any number from the set $61-75$.
To find the number of distinct possibilities, we multiply the number of choices for each position:
15 choices for the first number × 15 choices for the second number × 15 choices for the third number × 15 choices for the fourth number × 15 choices for the fifth number
To know more about diagonal visit:
https://brainly.com/question/33716087
#SPJ11
in a manufacturing process a machine produces bolts that have an average length of 3 inches with a variance of .03. if we randomly select three bolts from this process: what is the standard deviation of the sampling distribution of the sample mean?
Answers
The standard deviation of the sampling distribution of the sample mean is 0.1 when a machine produces bolts that have an average length of 3 inches with a variance of .03.
What is standard deviation?The positive square root of the variance is the standard deviation. One of the fundamental techniques used in statistical analysis is standard deviation. Standard deviation, also known as SD or denoted by the symbol "σ" indicates how far a value deviates from the mean value.
Here,
σx = σ/√n
= √.03/√3
= .1732/1.732
= 0.1
When a machine creates bolts with an average length of 3 inches and a variance of.03, the standard deviation of the sampling distribution of the sample mean is 0.1.
To know more about standard deviation,
https://brainly.com/question/13905583?referrer=searchResults
#SPJ4
find the point on the plane 8x − y + 8z = 80 nearest the origin.
Answers
The point on the plane 8x - y + 8z = 80 nearest the origin is (5, -10, 5).
To find the point on the plane 8x − y + 8z = 80 nearest the origin, we need to use the concept of distance between a point and a plane. Let's assume that the point we are looking for is (a, b, c). We know that the distance between the point and the plane is given by the formula:
distance = |ax + by + cz - d| / √(a^2 + b^2 + c^2)
where d is the constant in the equation of the plane.
In this case, the equation of the plane is 8x - y + 8z = 80. Therefore, a = 8, b = -1, c = 8, and d = 80.
The distance between the point (a, b, c) and the origin (0, 0, 0) is simply the length of the vector (a, b, c). Thus, we need to minimize the length of the vector (a, b, c) subject to the constraint that the point (a, b, c) lies on the plane 8x - y + 8z = 80.
We can use Lagrange multipliers to solve this problem. The Lagrangian function is given by:
L(a, b, c, λ) = a^2 + b^2 + c^2 + λ(8a - b + 8c - 80)
Taking the partial derivatives of L with respect to a, b, c, and λ and setting them equal to zero, we obtain the following system of equations:
2a + 8λ = 0
2b - λ = 0
2c + 8λ = 0
8a - b + 8c - 80 = 0
Solving for a, b, c, and λ, we get:
a = 5
b = -10
c = 5
λ = -1/2
we have found that the point on the plane 8x − y + 8z = 80 nearest the origin is (5, -10, 5). To solve this problem, we used the concept of distance between a point and a plane, which states that the distance between a point (a, b, c) and a plane ax + by + cz = d is given by |ax + by + cz - d| / √(a^2 + b^2 + c^2). We minimized the distance between the origin and the point on the plane subject to the constraint that the point lies on the plane. Using Lagrange multipliers, we obtained the point (5, -10, 5) as the solution to the problem.
To know more about origin visit:
https://brainly.com/question/30970730
#SPJ11
Guys why is my cas giving the wrong answers … is it on wrong settings ?

Answers
Answer:
those are the right answers
Step-by-step explanation:
for sin90 you have to put sin(90) which is 1, all the other answers r correct (same with my calculator)
Consider the function f (x) = x4 − 18x2 +10,
−2student submitted image, transcription available belowxstudent submitted image, transcription available below7.
Find the absolute minimum value of this function.
ALSO,
Find the absolute maximum value of this function.
Answers
Answer:
maximum: 10
minimum: -71
Step-by-step explanation:
The absolute minimum and maximum points of a function are the points where the instantaneous slope, or derivative, is 0.
To find these points, we first need find the general form for the derivative of the function:
\(f(x) = x^4 - 18x^2+10\)
↓ applying the sum/difference rule ... \(\left[ \dfrac{}{}f(x) \pm g(x)\dfrac{}{}\right]' = f'(x) \pm g'(x)\)
\(f'(x) = (x^4)' - (18x^2)' + (10)'\)
↓ applying the power rule ... \((x^a)' = ax^{(a-1)}\)
\(f'(x) = 4x^3 - 18(2x) + 0\)
\(f'(x) = 4x^3 - 36x\)
Now, we can plug in 0 for f'(x) to find the minimum and maximum points.
\(0 = 4x^3 - 36x\)
↓ factoring a 4x out of the right side
\(0 = 4x(x^2 - 9)\)
↓ applying the difference of squares formula ... \(x^2 - a^2 = (x + a)(x - a)\)
\(0 = 4x(x + 3)(x - 3)\)
↓ splitting into 3 equations ... \(\text{if } ABC = 0,\text{ then } A = 0 \text{ or } B=0 \text{ or } C = 0\)
\(4x = 0\) or \(x + 3 = 0\) or \(x-3=0\)
\(x = 0\) or \(x = -3\) or \(x = 3\)
Finally, we can plug these x-values back into the function to find the function's maximum and minimum y-values.
when x = 0...
\(f(0) = 0^4 - 18(0^2)+10\)
\(f(0) = 10\)
when x = -3...
\(f(-3) = (-3)^4 - 18(-3)^2 + 10\)
\(f(-3) = 81 - 162 + 10\)
\(f(-3) = -71\)
when x = 3...
\(f(3) = (3)^4 - 18(3)^2 + 10\)
\(f(3) = 81 - 162 + 10\)
\(f(3) = -71\)
So, the maximum y-value of the function is 10 and the minimum y-value is -71.
Give another name for RS.

Answers
Parallelogram Properties - Angles

Answers
Answer: x=30°
Step-by-step explanation:
A parallelogram always add up to 360°.
Opposite angles like F and H are always the same, so H=150°.
150+150=300 (what angles F and H add up to)
So we can do:
360-300=60
Now we know that the angle x and E have to add up to 60 but still be the same, so x will equal 30°.
We can check this by adding up all of the sides:
150+150+30+30=360°
Hope this helped :)
Find the 17th term of the arithmetic sequence –5, 1, 7, 13, …
A. 97
B. 107
C. 91
D. 87
Answers
Answer:
91
Step-by-step explanation:
the common diference is : d = ( 13)-(7)=(7)-(1)=(1)-(-5)=6
the first term is A1 = -5
the n-ieme term is : An = A1 +(n-1)d
An = -5+6(n-1)
An = 6n-11
the 17th term in the arithmetic sequence is : A17 = 6(17)-11 =91
Answer:
c
Step-by-step explanation:
-5,1,7,13,19,25,31,37,43,49,55,61,67,73,79,85,91
tan (tt/2) =. i neeed help baddddd

Answers
Answer:
D: Undefined
Step-by-step explanation:
You can use the unit circle or your calc for this (don't forget to put it in radians!). I will use the unit circle to explain.
Tangent on the unit circle is on the xy lines themselves. tan (π/2) would be on the positive y axis. Remember that tan∅ is sin∅/cos∅ and that the unit circle's radius is always one. If that is the case, the coordinate for tan (π/2) would be (0, 1). If cos is always x and sin is always y, you plug it in for tan∅. The fraction 1/0 is undefined, since you can't divide anything by 0. Therefore, tan (π/2) is undefined.
X
-9
-5
-1
3
Y
- 2
0
2
4
What is the slope of the line?
Answers
ok done. Thank to me :>

calculate the volume of this solid if the base is a regular pentagon of area 27, and the altitude of the pyramid is 7
Answers
The volume of the solid is 63 cubic units.
To calculate the volume of a pyramid, you can use the formula:
Volume = (1/3) * Base Area * Height
In this case, the base is a regular pentagon with an area of 27 and the altitude (height) of the pyramid is 7.
First, let's find the side length of the pentagon. Since a regular pentagon has all sides and angles equal, we can use the following formulas:
Area = (5/4) * side^2 * cot(pi/5)
27 = (5/4) * side^2 * cot(pi/5)
Now we solve for side:
side^2 = (27 * 4) / ((5/4) * cot(pi/5))
side^2 = 108 / ((5/4) * cot(pi/5))
side^2 = 108 * (4/5) * tan(pi/5)
side^2 = 86.4
side ≈ √86.4
side ≈ 9.306
Now we can calculate the volume using the formula:
Volume = (1/3) * Base Area * Height
Volume = (1/3) * 27 * 7
Volume = 63 cubic units
Therefore, the volume of the solid is 63 cubic units.
Learn more about volume from
https://brainly.com/question/27710307
#SPJ11
a bridge hand consists of 13 cards dealt at random from the deck of 52. the probability that a bridge hand will have exactly 2 queens is:
Answers
The probability that a bridge hand will have exactly 2 queens is 0.45%.
To find the probability of getting a bridge hand with exactly 2 queens, we need to use the binomial probability formula. The formula is:
P(exactly k successes) = (n choose k) * p^k * (1-p)^(n-k)
Where:
n is the total number of trials
k is the number of successes in the trials
p is the probability of success in a single trial
In this case, the total number of trials is 13 (since a bridge hand consists of 13 cards), and the number of successes we want is 2 (since we want exactly 2 queens). The probability of success in a single trial is the probability of drawing a queen, which is 4/52 (since there are 4 queens in a deck of 52 cards).
Plugging these values into the formula, we get:
P(exactly 2 queens) = (13 choose 2) * (4/52)² * (48/52)¹¹
= (78) * (1/169) * (4/13)¹¹
= (4/169) * (4/13)¹¹
This simplifies to:
P(exactly 2 queens) = (4/169) * (4/13)¹¹
= (4/169) * (4/169)¹¹
= (4/169)¹²
The final probability is approximately 0.0045 or 0.45%. This means that the probability of getting a bridge hand with exactly 2 queens is quite low.
Learn more about Probability at:
brainly.com/question/24756209
#SPJ4
Function f is defined as f(x)=x²-3x+5.
Drag a number below into each box below.
-29
-11
11
29
non-real
real
The discriminant is
This indicates there are two ___ roots
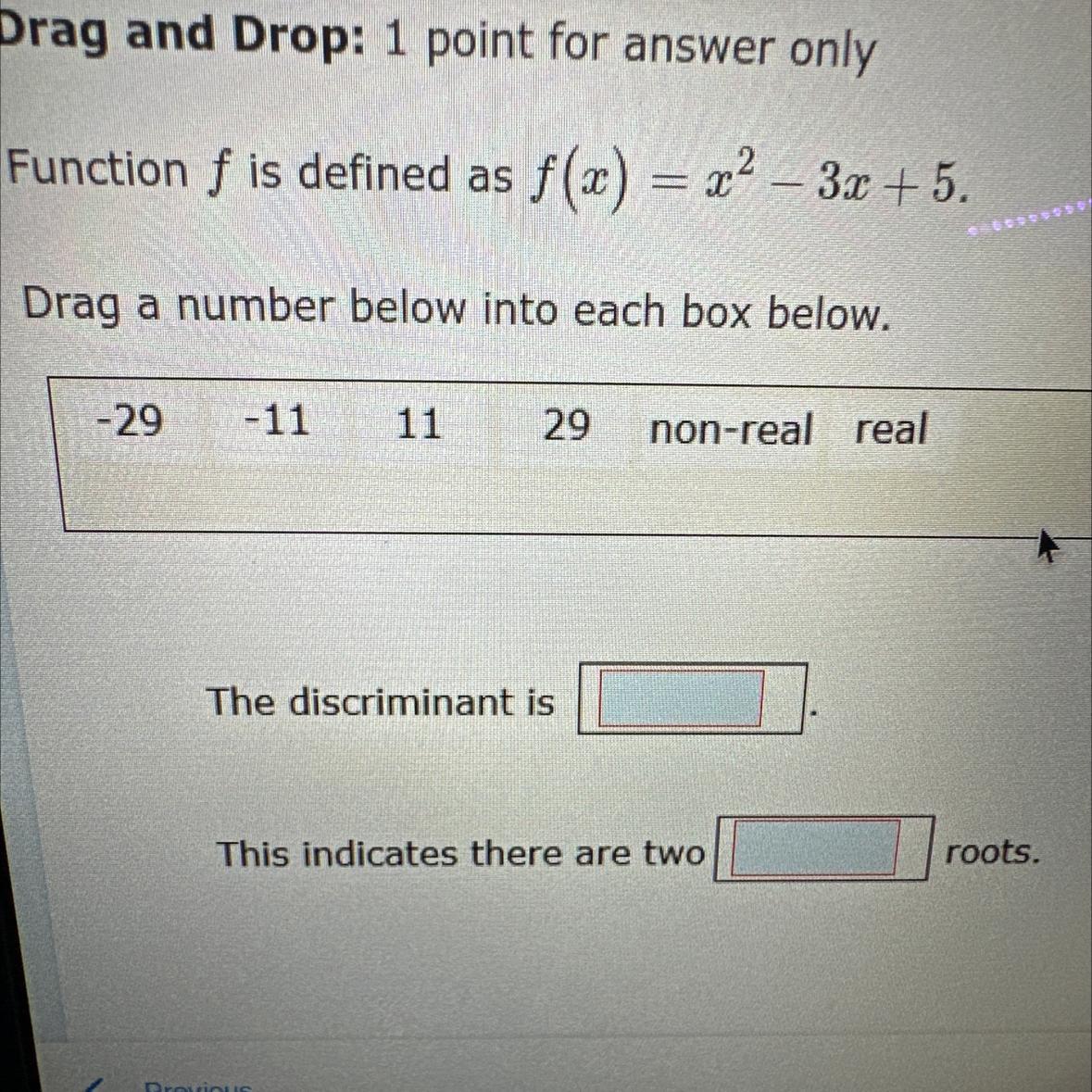
Answers
The discriminant is -11 and the roots are 3±√-11)/2.
What is a quadratic equation?
Any equation that can be written in the standard form where x is an unknown value, a, b, and c are known quantities, and a 0 is a quadratic equation.
Here, we have
Given: f(x)=x²-3x+5.
We have to find the discriminant and the two roots.
f(x) = x²-3x+5 is of the form ax²+bx+c, where a= 1, b= -3, c = 5
Its discriminant Δ is given by the formula:
Δ = b²-4ac = (-3)²-4×1×5
Δ = -11
Δ<0 then the equation has no real roots (it has two distinct complex roots).
The solutions of x²-3x+5 are given by the quadratic formula:
x = (-b ±\(\sqrt{b^2-4ac}\))/2a
x = 3±√-11)/2
Hence, the discriminant is -11 and the roots are 3±√-11)/2.
To learn more about the quadratic equation from the given link
https://brainly.com/question/30951539
#SPJ1
Please HELP ME pls I WILL BRAINLIST U please AND MARK U 5 star THIS IS URGENT IF U ARE SOMEONE WHO IS GOOD WITH MATHS THIS ONES FOR U!!!
Brian is a mobile phone sales person who earns $250 per week and $10 every phone that he sells.
a) write this as a formula with n representing the number of phone sold, and p representing the amount of money earned each week.
b) if 20 phones are sold the next week, how much money does Brian earn that week?
Answers
Answer:
n=30p=450
Step-by-step explanation:
10n+250=p
10×20+250=450
n=20 p=450
Your car can drive 380 miles on a tank of 22 gallons.
a. How far can it drive on 50 gallons? Round your answer to the nearest
hundredth.
b. How many gallons are needed to drive 650 miles? Round your answer to the
nearest hundredth.
Answers
Answer:
a) 863.6miles b) 37.6 gallons
Step-by-step explanation:
1) 380/22=17.27- miles can be driven due to 1 gallon
a) 380/22*50=863.6
b)650/380/22=37.6
The car will go 863.63 miles, and the number of gallons 37.63 that will be needed to drive 650 miles.
What is the distance?Distance is a numerical representation of the distance between two items or locations. Distance refers to a physical length or an approximation based on other physics or common usage considerations.
It is given that:
Your car can drive 380 miles on a tank of 22 gallons.
To find how far the car will go:
= 380/22
= 17.27
= (380/22)x50
= 863.63 miles
= (650/380)x22
= 37.63 gallons
Thus, the car will go 863.63 miles, and the number of gallons 37.63 that will be needed to drive 650 miles.
Learn more about the distance here:
brainly.com/question/26711747
#SPJ2
You and your friends decide to rent some studio time to make a CD. Big Notes Studio rents for $100 plus $60 per hour. Great Sounds Studio rents for $25 plus $80 per hour. Determine the number of hours for which the cost of 1 Step renting the studios is the same. Work needs to be showed btw
Answers
The solution is found by slope of the graph and the solution is 2,200.
Let x the amount of money per hour and y the total amount of money.
Studio A:-
Rents for 100 dollars plus 50 dollars per hour.
\(y= 100 + 50x\)
So the slope is 50 and the y intercept is 100.
Studio B:-
rents for 50 dollars plus 75 dollars per hour.
\(y= 50 + 75x\)
So the slope is 75 and the y intercept is 50.
ThrTh solution is 2200 , see the gragraphph.
To know more about Slope of graph go through:-
https://brainly.com/question/3493733
#SPJ4
Complete question:- You and your friends decide to rent some studio time to make a CD. Big Notes Studio rents for $100 plus $50 per hour. Great Sounds Studio rents for $50 plus $75 per hour. Solve the system by graphic method.

A test to measure aggressive tendencies was given to a group of teenage boys who were members of a street gang. The test is scored from 10 to 60, with a high score indicating more aggression. The histogram represents the results for these 28 boys.
5 4 125 175 225 275 325 375 425 475 aggress
What is the shape of the distribution? What measure of center should be used to report the typical value? What measure of spread would be the most appropriate measure to report how spread out the observations are in this histogram? Justify your choices.
Answers
It's important to note that the mean is not an appropriate measure of center for this data set since it can be heavily influenced by the outliers in the higher range of the distribution.
The shape of the distribution in the histogram appears to be skewed to the right. This means that there are more scores in the lower range, with a few outliers at the higher range.
The most appropriate measure of center to report the typical value is the median, since the data is not normally distributed. The median represents the middle value of the data set.
The most appropriate measure of spread to report how spread out the observations are in this histogram is the interquartile range (IQR). The IQR is the difference between the upper and lower quartiles, which provides an indication of the amount of spread in the data. This is especially important for skewed distributions, as it ignores any outliers in the data.
Learn more about measure of spread: https://brainly.com/question/30624135
#SPJ11
The first term of an arithmetic progression is 3 and the fifth term is 9. Find the number of terms in the progression if the last term is 81.
Answers
Answer:
n = 53
Step-by-step explanation:
the sum to n terms of an arithmetic progression is
\(a_{n}\) = a₁ + (n - 1)d
where a₁ is the first term and d the common difference
here a₁ = 3 and a₅ = 9 , then
3 + 4d = 9 ( subtract 3 from both sides )
4d = 6 ( divide both sides by 4 )
d = 1.5
then solving for n
3 + 1.5(n - 1) = 81 ( subtract 3 from both sides )
1.5(n - 1) = 78 ( divide both sides by 1.5 )
n - 1 = 52 ( add 1 to both sides )
n = 53
there are 53 terms in the progression
Answer:
53 terms
Step-by-step explanation:
Finding common difference :
a = 3a + 4d = 94d = 6d = 1.5Solving :
a_{n} = a + (n - 1)d81 = 3 + 1.5n - 1.579.5 = 1.5nn = 53What is the base of the expression 11 and 12 square? 3 11 12 21
Answers
Answer:
your answer is 11
Step-by-step explanation:
An exponential has the base at the bottom
use the multiplier method to increase £88 by 14 %
you must show ur workings
Answers
88£ + 12.32£ = 100.32£
two wires lie perpendicular to the plane of the paper
Answers
a. The resultant magnetic field at point P due to currents in the two wires can be determined by vector addition of the individual magnetic fields.
b. Reversing the direction of currents in both wires would result in a reversed direction of the resultant magnetic field at point P.
a. To construct the vector diagram showing the direction of the resultant magnetic field at point P due to currents in the two wires, we can use the right-hand rule for determining the magnetic field direction around a wire carrying current.
For Wire 1, which has the current coming towards us (out of the plane of the paper), the magnetic field direction can be determined by wrapping the right-hand fingers around the wire in the direction of the current, and the thumb will point in the direction of the magnetic field. Let's say the direction of the magnetic field for Wire 1 is from left to right.
For Wire 2, which has the current going into the plane of the paper, we apply the right-hand rule again. Wrapping the right-hand fingers around the wire in the direction opposite to the current, the thumb will point in the direction of the magnetic field. Let's say the direction of the magnetic field for Wire 2 is from right to left.
At point P, which is equidistant from the two wires, the magnetic fields due to the currents in the wires will combine. The resultant magnetic field direction at point P can be found by vector addition. Drawing the vectors representing the magnetic fields for Wire 1 and Wire 2, with opposite directions, we can add them head-to-tail. The resultant vector will show the direction of the resultant magnetic field at point P.
b. If the currents in both wires were instead directed into the plane of the page (such that the current moved away from us), the directions of the magnetic fields due to the currents in the wires would be reversed compared to the previous case.
For Wire 1, the magnetic field direction would be from right to left, and for Wire 2, it would be from left to right. Following the same process as in part a, we would draw the vectors representing the magnetic fields for Wire 1 and Wire 2 in their respective reversed directions. Adding them head-to-tail would give us the resultant vector indicating the direction of the resultant magnetic field at point P in this scenario.
Complete Question:
Two wires lie perpendicular to the plane of the paper, and equal electric currents pass through the paper in the directions shown. Point P is equidistant from the two wires.
a. Construct a vector diagram showing the direction of the resultant magnetic field at point P due to currents in these two wires. Explain your reasoning.
b. If the currents in both wires were instead directed into the plane of the page (such that the current moved away from us), show the resultant magnetic field at point P.
To know more about magnetic field, refer here:
https://brainly.com/question/14848188
#SPJ4
If x=4 then 2(x-4) equals
Answers
Now, according to PEMDAS, solve inside the parentheses first: 2(0)
Lastly, we can multiply: 2 x 0 = 0
Answer:
0
Step-by-step explanation:
Need to plug in the x to the 4 then u get 2(4-4)
After that it will equal to 0 the 4-4
2(0)=0
the length of a rectangle is 3n+ 2 and its width is n-1. The perimeter of the rectangle is twice the sum of its length and its width.
Find the perimeter of the rectangle when n = 4 inches.
Answers
Answer:
34 inches
Step-by-step explanation:
Let W be the width (in inches) and L be the length (inches).
Perimeter = 2W + 2L
This can be written as 2(W + L) [The perimeter of the rectangle is twice the sum of its length and its width.]
For n = 4 inches, we have:
L = 3n+2
L = 3(4) + 2
L = 14 inches
W = n - 1
W = 4 - 1
W = 3 inches
Perimeter = 2(W + L)
Perimeter = 2(3" + 14")
Perimeter = 34"
Consider the following function.f(x) = 6 − |x − 8|

Answers
Soution:
Given the function;
\(f(x)=6-|x-8|\)(a) Critcal points are points where the function is defined and the derivative is zero or undefined.
Absolute value functions are piecewise function;
Hence, the critical number of f is;
\(x=8\)Part A: Solve for the "h." Show all work

Answers
Answer:
2.7 m
Step-by-step explanation:
Corresponding sides of similar triangles are proportional. This figure shows similar triangles ∆ABC ~ ∆ADE.
__
The proportion that can be used to find h = DE is ...
DE/BC = DA/BA
h/(0.9 m) = (12 m+6 m)/(6 m) . . . . . filling in the values given
h = (0.9 m)(18/6) . . . . . multiply by 0.9 m
h = 2.7 m
The value of "h" is 2.7 m.
The unit measure for atmospheric pressure is kPa (Kilo-Pascals). At sea level the standard
atmospheric pressure is 101.3 kPa. For every 1000 feet increase in altitude, atmospheric
pressure decreases by 1.8 kPa. What is the atmospheric pressure at 50,000 feet?
Answers
The pressure change is an illustration of an arithmetic progression.
The atmospheric pressure at 50000 feet is 11.3 kPa
The given parameters are:
\(\mathbf{a = 101.3}\) --- the first term
\(\mathbf{d = -1.8 per 1000}\) -- common difference
At 50000 feet, the number of increment in altitude is
\(\mathbf{n = \frac{50000}{1000}}\)
\(\mathbf{n = 50}\)
So, the atmospheric pressure at 50000 feet is:
\(\mathbf{T_{50} = 101.3 - 1.8 \times 50}\)
\(\mathbf{T_{50} = 101.3 - 90}\)
\(\mathbf{T_{50} = 11.3}\)
Hence, the atmospheric pressure at 50000 feet is 11.3 kPa
Read more about arithmetic progressions at:
https://brainly.com/question/13989292
I have enough pure silver to coat 4 square meters of surface area. I plan to coat a sphere and a cube. Allowing for the possibility of all the silver going onto one of the solids, what dimensions should they be if the total volume of the silvered solids is to be a maximum
Answers
For maximum volume: Coat the sphere with a radius of approximately 0.5641 meters.
For minimum volume: Coat the cube with an edge length of approximately 0.8165 meters.
To determine the dimensions of the sphere and the cube that maximize and minimize the total volume of the silvered solids, we need to establish some equations and constraints based on the given information.
Let's denote the radius of the sphere as 'r' and the edge length of the cube as 'a'.
Maximizing the Total Volume:
For the maximum volume, we need to consider the possibility that all of the silver can be coated on either the sphere or the cube. We can set up two scenarios:
1) If all of the silver is coated on the sphere:
The surface area of a sphere is given by the formula:
A(sphere) = 4πr²
Since we have enough silver to cover 4 square meters, we can set up the equation:
4 = 4πr²
r² = 1/π
r ≈ 0.5641
So, if all of the silver is coated on the sphere, the radius should be approximately 0.5641 meters.
2) If all of the silver is coated on the cube:
The surface area of a cube is given by the formula:
A(cube) = 6a²
Again, considering that we have enough silver to cover 4 square meters, we can set up the equation:
4 = 6a²
a² = 2/3
a ≈ 0.8165
If all of the silver is coated on the cube, the edge length should be approximately 0.8165 meters.
Minimizing the Total Volume:
For the minimum volume, we need to consider the case where one solid is entirely coated with the silver, while the other solid remains uncoated.
1) If all of the silver is coated on the sphere:
In this case, the volume of the sphere will be maximum, and the cube will remain uncoated.
We can calculate the volume of the sphere using the formula:
V(sphere) = (4/3)πr³
Substituting the value of r we obtained earlier (r ≈ 0.5641), we can find the volume of the sphere:
V(sphere) ≈ (4/3)π(0.5641)³ ≈ 0.7556 cubic meters
2) If all of the silver is coated on the cube:
In this case, the volume of the cube will be maximum, and the sphere will remain uncoated.
We can calculate the volume of the cube using the formula:
V(cube) = a³
Substituting the value of a we obtained earlier (a ≈ 0.8165), we can find the volume of the cube:
V(cube) ≈ (0.8165)³ ≈ 0.5352 cubic meters
Therefore, if we want to minimize the total volume, we should coat the cube, resulting in a volume of approximately 0.5352 cubic meters, while leaving the sphere uncoated.
To summarize:
For maximum volume: Coat the sphere with a radius of approximately 0.5641 meters.
For minimum volume: Coat the cube with an edge length of approximately 0.8165 meters.
Learn more about volume click;
https://brainly.com/question/28058531
#SPJ4
i dont understand someone help me please help help help!!! pleasee

Answers
Answer:
\(r=\sqrt{R^2-\dfrac{V}{\pi h}}\)
Step-by-step explanation:
You are being asked to solve the volume equation for r. We find that r is squared, added to something, the sum is multiplied by something. We want to undo those operations, in reverse order.
\(V=\pi h(R^2-r^2)\\\\\dfrac{V}{\pi h}=R^2-r^2\qquad\text{divide by $\pi h$}\\\\r^2=R^2-\dfrac{V}{\pi h}\qquad\text{add $r^2-V/(\pi h)$}\\\\\boxed{r=\sqrt{R^2-\dfrac{V}{\pi h}}}\qquad\text{square root}\)
Sunil stated that three points determine a unique plane. Explain Sunil's error and give a corrected statement.
Answers
Answer:
three points gives triangle. two points gives a straight line.