a desert tray has three slices of cake, three key lime pies, and four ice cream sundaes. What is the probability of the next two customers both select key lime pie?
Answers
Answer:
The probability of the next two customers both select key lime pie is 1/15
Step-by-step explanation:
No. of slices of cakes = 3
No. of key lime pies = 3
No. of ice cream sundaes = 4
Total deserts = 3+3+4=10
We are supposed to find The probability of the next two customers both select key lime pie
Probability of selecting key lime pie by first customer =\(\frac{3}{10}\)
So,Total deserts =10-1=9
No. of key lime pies = 3-1=2
So,Probability of selecting key lime pie by second customer = \(\frac{2}{9}\)
So,the probability of the next two customers both select key lime pie=\(\frac{3}{10} \times \frac{2}{9} =\frac{1}{15}\)
Hence the probability of the next two customers both select key lime pie is 1/15
Related Questions
There are 96 football players at all levels at Davenport High School. If two-thirds of the players make the honor roll for their grades how many olayers are on the list?
64 players
48 players
72 players
54 players
Answers
Reason- 2/3 of 96 = (32 x 2 = 64) telling us how many got on the list
The distances, in light years, of four stars from a space probe are shown. Put the stars in order from the closest one (least distance) to the farthest one (greatest distance). 0.886 0.883 1.25 0.89
A.
0.883, 0.886, 0.89, 1.25
B.
0.883, 0.886, 1.25, 0.89
C.
1.25, 0.89, 0.886, 0.883
D.
0.886, 0.883, 0.89, 1.25
Answers
The stars in order from the closest one to the farthest one are:
0.883, 0.886, 0.89, 1.25
so, the answer is A.
What is a sequence?
A sequence is an enumerated collection of objects in which repetitions are allowed. Like a set, it contains members (also called elements, or terms).
To put the given distances in order from the closest one to the farthest one, we need to arrange them in ascending order.
That means we need to start with the smallest value and move toward the largest value.
Looking at the given distances, we see that the smallest value is 0.883, followed by 0.886, then 0.89, and finally 1.25, which is the largest value.
Putting the given distances in ascending order, we get:
0.883, 0.886, 0.89, 1.25
Therefore, the stars in order from the closest one to the farthest one are:
0.883, 0.886, 0.89, 1.25
so, the answer is A.
To know more about sequence visit:
brainly.com/question/12246947
#SPJ1
Please only answer if u actually know pls!

Answers
At a price of $3, the total revenue will be the greatest, and the company will sell 3 units at that price.
To find the total revenue at each price, we can multiply the price by the corresponding quantity.
Price Quantity Total Revenue
$6 0 $0
$5 1 $5
$4 2 $8
$3 3 $9
$2 4 $8
$1 5 $5
To find the price at which total revenue is the greatest, we look for the highest value in the Total Revenue column.
In this case, the highest total revenue is $9, which occurs when the price is $3.
At a price of $3, the company will sell 3 units (as indicated in the Quantity column).
To learn more on Revenue click:
https://brainly.com/question/14952769
#SPJ1
x: 7x2-3x=2
ALGEBRA TWO

Answers
X2 =3+(square root of 64) divided by 14
if i compare 0.10__0.01 what would the answer be?

Answers
The answer will be 0. 10 > 0. 01 . Option B
How to compare the valuesGiven the values as;
0.100.01Turn the values into proper fractions
a. 0. 10 = 10/ 100
Reduce to simpler terms
= 10/ 100
= 1/ 10
b. 0. 01 = 1/ 100
a = 1/ 100
b = 1/ 100
This means that both decimals are not of equal proportion and thus a is greater than (>) b
Thus, the answer will be 0. 10 > 0. 01 . Option B
Learn more about decimals here:
https://brainly.com/question/1827193
#SPJ1
According to an NRF survey conducted by BIGresearch, the average family spends about $237 on electronics (computers, cell phones, etc.) in back-to-college spending per student. Suppose back-to-college family spending on electronics is normally distributed with a standard deviation of $54. If a family of a returning college student is randomly selected, what is the probability that: (a) They spend less than $150 on back-to-college electronics? (b) They spend more than $390 on back-to-college electronics? (c) They spend between $120 and $175 on back-to-college electronics?
Answers
Answer:
(a) Probability that a family of a returning college student spend less than $150 on back-to-college electronics is 0.0537.
(b) Probability that a family of a returning college student spend more than $390 on back-to-college electronics is 0.0023.
(c) Probability that a family of a returning college student spend between $120 and $175 on back-to-college electronics is 0.1101.
Step-by-step explanation:
We are given that according to an NRF survey conducted by BIG research, the average family spends about $237 on electronics in back-to-college spending per student.
Suppose back-to-college family spending on electronics is normally distributed with a standard deviation of $54.
Let X = back-to-college family spending on electronics
SO, X ~ Normal(\(\mu=237,\sigma^{2} =54^{2}\))
The z score probability distribution for normal distribution is given by;
Z = \(\frac{X-\mu}{\sigma}\) ~ N(0,1)
where, \(\mu\) = population mean family spending = $237
\(\sigma\) = standard deviation = $54
(a) Probability that a family of a returning college student spend less than $150 on back-to-college electronics is = P(X < $150)
P(X < $150) = P( \(\frac{X-\mu}{\sigma}\) < \(\frac{150-237}{54}\) ) = P(Z < -1.61) = 1 - P(Z \(\leq\) 1.61)
= 1 - 0.9463 = 0.0537
The above probability is calculated by looking at the value of x = 1.61 in the z table which has an area of 0.9463.
(b) Probability that a family of a returning college student spend more than $390 on back-to-college electronics is = P(X > $390)
P(X > $390) = P( \(\frac{X-\mu}{\sigma}\) > \(\frac{390-237}{54}\) ) = P(Z > 2.83) = 1 - P(Z \(\leq\) 2.83)
= 1 - 0.9977 = 0.0023
The above probability is calculated by looking at the value of x = 2.83 in the z table which has an area of 0.9977.
(c) Probability that a family of a returning college student spend between $120 and $175 on back-to-college electronics is given by = P($120 < X < $175)
P($120 < X < $175) = P(X < $175) - P(X \(\leq\) $120)
P(X < $175) = P( \(\frac{X-\mu}{\sigma}\) < \(\frac{175-237}{54}\) ) = P(Z < -1.15) = 1 - P(Z \(\leq\) 1.15)
= 1 - 0.8749 = 0.1251
P(X < $120) = P( \(\frac{X-\mu}{\sigma}\) < \(\frac{120-237}{54}\) ) = P(Z < -2.17) = 1 - P(Z \(\leq\) 2.17)
= 1 - 0.9850 = 0.015
The above probability is calculated by looking at the value of x = 1.15 and x = 2.17 in the z table which has an area of 0.8749 and 0.9850 respectively.
Therefore, P($120 < X < $175) = 0.1251 - 0.015 = 0.1101
....................
Answers
Answer:
.........................
Step-by-step explanation:
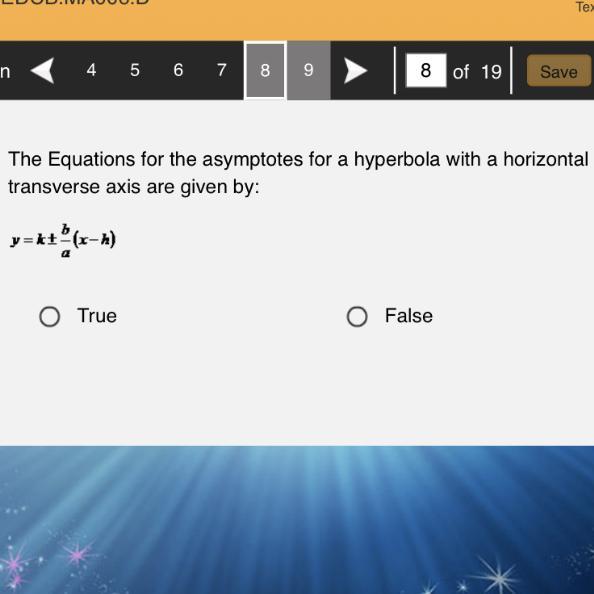
The Equations for the asymptotes for a hyperbola with a horizontal transverse axis are given by:y equals k plus or minus b over a times the quantity of x minus hTrueFalse
Answers
True, The given equation for the asymptotes for a hyperbola with horizontal transverse axis is y = k ± (b/a) (x - h).
Define Hyperbola
The collection of all points along a hyperbola such that the difference in distance between any point along the hyperbola and two fixed locations is constant is known as the hyperbola. The foci of the hyperbola are the two fixed points.
The standard equation for a hyperbola with a horizontal transverse axis is
(x - h)² / a² - (y - k)² / b² = 1
The distance between the vertices is 2a.
Every hyperbola has two asymptotes
A hyperbola with a horizontal transverse axis and center at (h, k) has one asymptote with equation
y = k + (b/a) (x - h)
and the other with equation
y = k - (b/a) (x - h)
Therefore, the answer is True.
To read more about Hyperbola.
https://brainly.com/question/26250569
#SPJ9
Make a dot plot for each set of data. Compare and contrast the shape, spread, and center of the data.
Set A = {4, 5, 6, 3, 3, 2, 4, 5, 8, 2, 5, 13}
Set B = {5, 6, 4, 2, 8, 4, 5, 6, 5, 2, 8, 3, 7, 3}
Answers
Set A has a peak at 5. It is also skewed to the right. The center is 5.
Set B also has a peak at 5. Is relatively symmetrical. The center is also 5.
(Sorry about those circle in the back of my picture)

PLEASE HELP I WILL MAKE YOU BRAINLIEST IF IT LETS ME
NO FAKE LINKS OR YOU WILL BE REPORTED

Answers
B:(4,2)
C:(1/2,1/4)
D:(1,2 1/2)
E:(1 3/4, 4 1/4)
Help me please, Which equation can be used to find the value of x?
Worth 20

Answers
Answer:
168 = 18 * x + 12 * 2x
Step-by-step explanation:
It's the only one that makes sense. You can mark out the 2nd and last one. We don't add 2x + x; for the 3rd, they need to subtract 18 - 2x, so that's not right either.
Can someone help me please
A population of bacteria is growing according to the equation p(t)=1950e^0.16t Estimate when the population will exceed 6371.
t= -------------
Answers
The estimate for when the population will exceed 6371 is t > 20.33. This means that at a time greater than 20.33 units
How to deal with exponential function?To estimate when the population will exceed 6371, we can set up the inequality:
p(t) > 6371
where p(t) is the population at time t, as given by the equation \(p(t) = 1950e^{0.16t}\)
Substituting the expression for p(t) into the inequality, we get:
\(1950e^{0.16t} > 6371\)
Next, we can divide both sides of the inequality by 1950 to isolate the exponential term:
\(e^{0.16t} > 6371 / 1950\)
To solve for t, we can take the natural logarithm (ln) of both sides, which will eliminate the exponential term:
\(ln(e^{0.16t} > ln(6371 / 1950)\)
Using the property of logarithms that ln(e^x) = x, we get:
\(0.16t > ln(6371 / 1950)\)
Now, we can divide both sides of the inequality by 0.16 to solve for t:
\(0.16t / 0.16 > ln(6371 / 1950) / 0.16\)
Simplifying, we get:
\(t > ln(6371 / 1950) / 0.16\)
Using a calculator, we can find the approximate value of \(ln(6371 / 1950) / 0.16\), which is approximately 20.33 (rounded to two decimal places).
So, the estimate for when the population will exceed 6371 is t > 20.33. This means that at a time greater than 20.33 units
To know more about Exponential function visit:
brainly.com/question/14355665
#SPJ1
what is the solution to the division problem below? (you can use long division or synthetic division.) PLEASE ANSWER

Answers
Answer: C
Step-by-step explanation: A P E X
C
Step-by-step explanation:
help please i will mark brainliest if the answer is correct

Answers
Answer:
2
-2
-1.5/7,-1)
-2
2
Step-by-step explanation:
Also your first answer is correct ma'am or sir! thank me later
Can someone help me out

Answers
Answer: a) x = .555...
=> 10x = 5.55...
=> 10x - x = 5.55... - .555...
=> 9x = 5
=> x = 5/9
b) x = .2525...
=> 100x = 25.25...
=> 100x - x = 25.25... - .2525...
=> 99x = 25
=> x = 25/99
2. A(n) is NOT an example of an agreement. (1 point)
O lease
O month-to-month
O annual
O fine print
Answers
An Annual is not an example of an agreement.
A car is traveling at a rate of 108 kilometers per hour. What is the cars rate in meters per second? How many meters will the car travel in 20 seconds?
Answers
Answer:
\(\frac{30meters}{second}\)
600meters
Step-by-step explanation:
Use conversion factors that represent 1. You can cross cancel wods just like numbers.
\(\frac{108km}{1hour}\) · \(\frac{1hour}{60 minutes}\) · \(\frac{1minute}{60seconds}\) ·\(\frac{1000meters}{1 km}\)
\(\frac{108000meters}{3600seconds}\)
\(\frac{30meters}{second}\)
\(\frac{30meters}{second}\) ·\(\frac{20seconds}{1}\)
600 meters
Helping in the name of Jesus.
Write the following numbers in order from smallest to largest. 27.56, 27.509, 27.5998, 27.599
Answers
Answer: 27.509, 27.56, 27.599, 27.5998
Step-by-step explanation:
For the question below, think carefully about what you divide 80 by to calculate the value of one part.
In a housing estate the direct proportion of flats to houses is 2:5. If there are 80 flats, how many houses are there?
Answers
Answer:
200
Step-by-step explanation:
\(\frac{2}{5}\) = \(\frac{80}{x}\)
2 x 40 = 80, so
5 x 40 = 200
Answer:
200 houses
Step-by-step explanation:
Flat: 2 parts = 80 flats
1 part => 80 : 2 = 40 flats
Houses: 5 parts = 40 x 5 = 200 houses
Let 0°
Given: tan a =2.4
Find: sin a and cos a

Answers
Answer:
sin α = 12/13;cos α = 5/13.-------------------------
Since angle α is between 0° and 90°, it is in the first quadrant and therefore all sin α, cos α and tan α are positive numbers.
Use the following identities:
tan α = sin α / cos α;sin² α + cos² α = 1.Given tan α = 2.4. Using identities, find cosine as follows:
sin α / cos α = 2.4sin α = 2.4 cos αcos² α = 1 - sin² αcos² α = 1 - (2.4 cos² α)²cos² α = 1 - 5.76 cos² αcos² α + 5.76 cos² α = 16.76 cos² α = 12.6 cos α = 1cos α = 1/2.6cos α = 10/26 cos α = 5/13Find sine:
sin² α = 1 - cos² αsin² α = 1 - (5/13)²sin² α = 1 - 25/169sin² α = 144/169sin α = 12/13what does -2.3f +0.4f-13-5 equal?
Answers
Answer:
-1.9f-18
Step-by-step explanation:
Evaluate like terms. (0.4f-2.3f) & (-13-5)
-2.3f+0.4f-13-5 = -1.9f-18
The word isometric can be broken into two parts. The prefix "iso-” means "of the same,” and "-metric” means "measure.” How does the meaning of the word isometric relate to determining if an isometric transformation occurred? Include the defining characteristics of angle measure and line segments in your response.
Answers
The term "isometric" has the Greek roots "isos," which means "same," and "metron," which means "measure." The definition of an isometric transformation is one in which the original figure and its transformed equivalent have the same shape, size, and orientation.
When we speak about geometric figures, the concept of shape, size, and orientation come into play.The defining characteristics of angle measure and line segments play a critical role in determining whether an isometric transformation has occurred. In geometry, angle measures are the measurements of angles in a geometric figure. An angle is formed by two line segments that share a common endpoint. It is a unit used to calculate the measure of a plane figure's interior or exterior, such as a polygon. In other words, the size of the angle doesn't change during an isometric transformation.Line segments are the building blocks of geometric figures. They are used to construct geometric figures such as polygons, triangles, and rectangles, among others. In an isometric transformation, the length of the line segments remains constant because the shape and size of the original figure and its transformed equivalent remain the same.In conclusion, the word "isometric" implies that the transformation has the same measurements of the original figure. It is a transformation that retains the original geometric figures' shape, size, and orientation. The defining characteristics of angle measure and line segments remain unchanged during the isometric transformation. This means that if an isometric transformation occurs, the original and transformed figures have the same measurements of angles and line segments.For such more question on isometric
https://brainly.com/question/14486229
#SPJ8
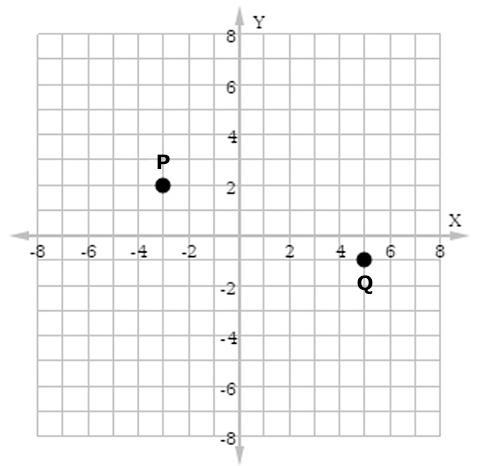
Find the distance between the points P and Q shown.

Answers
The distance between points P and Q is √73
How to find the distance between the two points?First, remember that the distance between two points whose coordinates are (a, b) and (c, d) is given by:
distance = √( (a - c)² + (b - d)²)
Here we can see that the coordinates of the two shown points are:
P = (-3, 2)
Q = (5, -1)
Replacing that in the distance formula we will get:
distance = √( (-3 - 5)² + (2 + 1)²)
distance = √( (-8)² + (3)²)
distance = √73
So the correct option is the third one.
Learn more about distance at:
https://brainly.com/question/7243416
#SPJ1
find the dirivative using first principle
\(f(x) = \frac{1}{x - 3 } \)
Answers
Step-by-step explanation:
\( {(x - 3)}^{ - 1} \\ = - (x - 3) \times (1) \\ = - (x - 3)\)
solve the following system of equations
1/2x+1/4y=-2
-2/3x+1/2y=6
x=
y=
Answers
Answer:
x = -6
y = 4
Step-by-step explanation:
Rewriting the equations :
2x + y = -84x - 3y = -36Now, solving the two equations using substitution method, we get :
x = -6
y = 4
Answer:
y = 4
x = -6
Step-by-step explanation:
1/2 x + 1/4 y= -2 first equation
-2/3 x + 1/2 y = 6 second equation
solution:
from the first equation:
8(1/2 x + 1/4 y) = -2*8
8x*1/2 + 8y*1/4 = -16
8x/2 + 8y/4 = -16
4x + 2y = -16 third equation
from the second equation
6(-2/3 x + 1/2 y) = 6*6
6x*-2/3 + 6y*1/2 = 36
-12x/3 + 6y/2 = 36
-4x + 3y = 36 fourth equation
from the third & fourth equation:
4x + 2y = -16
-4x + 3y = 36
0 + 5y = 20
5y = 20
y = 20/5
y = 4
from the fourth equation:
-4x + 3y = 36
-4x + 3*4 = 36
-4x + 12 = 36
-4x = 36 - 12
-4x = 24
x = 24/-4
x = -6
Check:
from the first equation:
1/2 x + 1/4 y = -2
1/2 *-6 + 1/4 * 4 = -2
-3 + 1 0 -2
from the second equation:
-2/3 x + 1/2 y = 6
-2/3 * -6 + 1/2 * 4 = 6
4 + 2 = 6
Cual es el perímetro de un rectángulo si tiene 20 de largo y 11 de ancho?
Answers
The perimeter of the rectangle is 62 square units.
How to find the perimeter of a rectangle?The perimeter of a rectangle can be calculated using the formula:
P = 2(L + W)
Where:
L is the length of the rectangle
W is the width of the rectangle
We have:
L = 20 units
W = 11 units
Substituting into the formula:
P = 2(20 + 11)
P = 2(31)
P = 62 square units
Learn more about perimeter of rectangle on:
https://brainly.com/question/19819849
#SPJ1
Question in English
What is the perimeter of a rectangle if it is 20 long and 11 wide?
c) Evaluate: 3√11x√2
Answers
Answer:
\(3\sqrt{22}\)
Step-by-step explanation:
The product of roots with the same index is equal to the root of the product \(3\sqrt{11*2}\)
Multiply
if the x is inside the square root
help me to solve i and ii. Genius people. answer of i is 41.82 and ii is 1585.45

Answers
Step-by-step explanation:
a 75% rebound ratio means that the rebounding back reaches 75% of the height of the previous drop.
75% = 3/4
a geometric series means that every term is created by multiplying the previous term by a certain factor. this factor is this mentioned 3/4.
each term (except s0, the start value) stands for the hight of the bounce.
s0 = k
s1 = s0 × 3/4 = k × 3/4
s2 = s1 × 3/4 = k × 3/4 × 3/4 = k × (3/4)²
sn = sn-1 × 3/4 = k × (3/4)^n
for k = 235ft
the 6th bounce is
s6 = 235 × (3/4)⁶ = 41.82495117... ft
the total distance by the ball is
2× the sum of the terms until s11 (the last bounce before the ball strikes the ground a 12th time) - s0.
why ? for s1 to s11 the ball has to go up and down, so the height of the bounce is traveled twice. but s0 happens only once (the first drop). so, when we multiply the whole sum by 2, we need to deduct s0 one time again.
the sum of all bounces s0 to s11 (n = 11) is
s = s0 × (1 - r^(n+1))/(1 - r)
where r is the multiplication factor (here 3/4).
s = 235 × (1 - (3/4)¹²)/(1 - 3/4) =
= 235 × (1 - (3/4)¹²)/(1/4) = 235 × (1 -(3/4)¹²) × 4 =
= 910.2242291... ft
2×s - s0 = 1,585.448458... ft
In an animal rescue facility are 21 animals.14 cats and 7 dogs. During the day 5 animals were adopted.what is the probabity that 3 cats and 2 dogs were adopted? Review ch 7 on probability
Answers
Answer:
0.3756
Step-by-step explanation:
I believe this is a combinatorics probability problem.
We first figure out in how many ways we can choose 3 cats out of 14 cats
Then we figure out how many ways we can choose 2 dogs out of 7 dogs
The total number of ways to select 3 cats and 2 dogs will be the product of these two
We then figure out in how many ways we can select 5 animals out of a total of 21 animals
The product we computed divided by the above number will give the probability
The number of ways we can choose k items out of n items is given by nCk i.e n Choose k
The formula is rather complicated but almost all calculators should be able to compute this given n and k
Let's deal with the selection of 3 cats from the population of 14 cats
This is given by 14C₃ which works out to 364
Number of ways for selecting 2 dogs from 7 dogs = 7C₂ = 21
Number of ways of selecting 5 animals from 21 = 21C₅ = 20349
The probability of selecting 3 cats and 2 dogs is therefore:
\(\dfrac{364 \times 21}{20349} = 0.3756\)
That, I believe is the answer. Please let me know if it is correct and if you need more info.
At a restaurant, your total bill is $81.95 . You wish to give a tip of 15% of the total bill. What is the amount of the tip? Round your answer to the nearest cent
Answers
Answer:
Step-by-step explanation:
Find 15 percent of 81.95 and add it to that.
The answer is 94.24 rounded.