A department store wraps gifts for its customers. What is the amount of wrapping paper it would take to wrap a gift box with a width of 8 inches, a height of 6 inches, and a length of 5 inches?
Answers
Answer:\(236\ in.^2\)
Step-by-step explanation:
Given
Dimension of gift box is
Width \(b=8\ in.\)
height \(h=6\ in.\)
Length \(L=5\ in.\)
So, box is in shape cubiod
and its surface area is given by
\(S.A.=2(lb+bh+hl)\)
\(S.A.=2(5\times 8+8\times 6+6\times 5)\)
\(S.A.=2(40+48+30)\)
\(S.A.=2\times 118\)
\(S.A.=236\ in.^2\)
So, \(236\ in.^2\) of gift paper is required
Related Questions
solve the following problems:
in Mrs. Pregonero Math class, 12 pupils got high scores on thw test . if this is 15% of the total number of pupils in the class, how many pupils she have in all?
Answers
Answer:
Step-by-step explanation:
tey to analyze the problems
Eastbound travels at 95 miles per hour the westbound train travels at 105 miles per hour .how long will it take for the two trains to be 480 miles apart
Answers
Answer:
48
Step-by-step explanation:
This is a linear equation, it goes as follows:
\(105(x) - 95(x) = 480\)
x stands for hours.
Solving for x yields 10.
Keep in mind that 105 and 95 are miles per hour where 480 is miles. So multiplying \((\frac{miles}{hours}) (hours)\) gives off hours which is what we are looking for.
Hope this helps.
The sum of three numbers is 65. The first number is 5 more than the second. The third number is 2 times the second. What are the numbers
Answers
Let the three numbers be a, b, and c.
a+b+c=65
The second number is 3 times the first.
b=3a.
This makes the sum a+3a+c=65.
The third number is 3 times the second. Consequently this also means that the third number is 9 times the first.
c=9a
This makes the sum a+3a+9a=65
13a/13=65/13
a=5
b=3a
b=15
c=3b
c=45
5+15+45=65, so the numbers are 5, 15, and 45.
What is the midpoint of the line segment graphed below?

Answers
Answer:
option A \((4, \frac{7}{2})\) is the midpoint.
Explanation:
To find midpoint: \((\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})\)
We shall use this formula here:
\((\frac{9+-1}{2}, \frac{5+2}{2})\)
\((\frac{8}{2}, \frac{7}{2})\)
\((4,3.5)\)
I am stumped with the graph question attached. Please assist.

Answers
Answer:
\(\begin{gathered} 0.44x^{2}-2.67x+3 \\ or \\ \frac{1}{2.25}(x-3)^2-1 \end{gathered}\)Explanation:
From the graph, we will observe that the vertex is at the point:
\(\begin{gathered} (h,k)=(3,-1) \\ \text{We will obtain the quadratic equation from the vertex form using the formula:} \\ f(x)=a(x-h)^2+k \\ \text{Inputting the values of ''h'' \& ''k'', we have:} \\ f(x)=a(x-3)^2-1 \\ \text{We have the x-intercept at point:} \\ (x,y)=(1.5,0) \\ f(1.5)=0 \\ \Rightarrow0=a(1.5-3)^2-1 \\ 0=a(-1.5)^2-1 \\ 0=a(2.25)-1 \\ 0=2.25a-1 \\ \text{Add ''1'' to both sides, we have:} \\ 1=2.25a \\ 2.25a=1 \\ \text{Divide both sides by ''2.25'', we have:} \\ a=\frac{1}{2.25}=0.44 \\ \text{We will substitute the value of ''a'' into the vertex equation, we have:} \\ f(x)=\frac{1}{2.25}(x-3)^2-1 \\ \text{Expand the bracket, we have:} \\ f(x)=\frac{1}{2.25}(x-3)(x-3)-1 \\ f(x)=\frac{1}{2.25}[x(x-3)-3(x-3)]-1 \\ f(x)=\frac{1}{2.25}[x^2-3x-3x+9]-1 \\ f(x)=\frac{1}{2.25}[x^2-6x+9]-1 \end{gathered}\)We will obtain the quadratic function as shown below:
\(\begin{gathered} \frac{1}{2.25}[x^2-6x+9]-1 \\ \text{Expand the bracket, we have:} \\ 0.44x^2-2.67x+4-1 \\ 0.44x^2-2.67x+3 \\ or \\ \frac{1}{2.25}(x-3)^{2}-1 \\ \end{gathered}\)What is equivalent to (7/4)(1/2)

Answers
Answer:
Answer is b(7/8)
Step-by-step explanation:
7/4×1/2=7/8
The solution is Option B.
The value of the equation is A = 7/8
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be represented as A
Now , the value of A is
Let the first number be p
The value of p = ( 7/4 )
Let the second number be q
The value of q = 1/2
A = p x q
Substituting the values in the equation , we get
A = ( 7/4 ) x ( 1/2 )
On simplifying the equation , we get
A = ( 7/8 )
Therefore , the value of A is 7/8
Hence , the equation is A = 7/8
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ2
Which of the following does NOT provide a buffer
against the effects of stress?
a. exercise
b. family and friends
c. optimism
d. smoking
Answers
d. smoking
This is the answer.
the price of a stock in a computer company is 25% greater than the cost of stock in a bank, b. write an expression for the sum of the prices of the stocks in the computer company in the bank in terms of b
Answers
Answer:
1.25b
Step-by-step explanation:
Let the cost of stock in a bank, b.
Now, since the price of a stock in a computer company is 25% greater than the cost of stock in a bank, it means;
the cost of stock in the computer company = b + 25%b = 1.25b
Thus,total cost of stock in both bank and computer company is;
Sum = 1.25b
A survey found that women's heights are normally distributed with mean 63.6 in and standard deviation 2.5 in. A branch of the military requires women's heights to be between 58 in and 80 in.
a. Find the percentage of women meeting the height requirement. Are many women being denied the opportunity to join this branch of the military because they are too short or too tall?
b. If this branch of the military changes the height requirements so that all women are eligible except the shortest 1% and the tallest 2%, what are the new height requirements?
Answers
Answer:
(A)
Step-by-step explanation:
The survey follows of women's height a normal distribution.
The height of 98.51% of women that meet the height requirement are between 58 inches and 80 inches.
The new height requirements would be 57.7 to 68.6 inches
The given parameters are:
\mathbf{\mu = 63.5}μ=63.5 --- mean
\mathbf{\sigma = 2.5}σ=2.5 --- standard deviation
(a) Percentage of women between 58 and 80 inches
This means that: x = 58 and x = 80
When x = 58, the z-score is:
\mathbf{z= \frac{x - \mu}{\sigma}}z=
σ
x−μ
This gives
\mathbf{z_1= \frac{58 - 63.5}{2.5}}z
1
=
2.5
58−63.5
\mathbf{z_1= \frac{-5.5}{2.5}}z
1
=
2.5
−5.5
\mathbf{z_1= -2.2}z
1
=−2.2
When x = 80, the z-score is:
\mathbf{z_2= \frac{80 - 63.5}{2.5}}z
2
=
2.5
80−63.5
\mathbf{z_2= \frac{16.5}{2.5}}z
2
=
2.5
16.5
\mathbf{z_2= 6.6}z
2
=6.6
So, the percentage of women is:
\mathbf{p = P(z < z_2) - P(z < z_1)}p=P(z<z
2
)−P(z<z
1
)
Substitute known values
\mathbf{p = P(z < 6.6) - P(z < -2.2)}p=P(z<6.6)−P(z<−2.2)
Using the p-value table, we have:
\mathbf{p = 0.9999982 - 0.0139034}p=0.9999982−0.0139034
\mathbf{p = 0.9860948}p=0.9860948
Express as percentage
\mathbf{p = 0.9860948 \times 100\%}p=0.9860948×100%
\mathbf{p = 98.60948\%}p=98.60948%
Approximate
\mathbf{p = 98.61\%}p=98.61%
This means that:
The height of 98.51% of women that meet the height requirement are between 58 inches and 80 inches.
So, many women (outside this range) would be denied the opportunity, because they are either too short or too tall.
(b) Change of requirement
Shortest = 1%
Tallest = 2%
If the tallest is 2%, then the upper end of the shortest range is 98% (i.e. 100% - 2%).
So, we have:
Shortest = 1% to 98%
This means that:
The p values are: 1% to 98%
Using the z-score table
When p = 1%, z = -2.32635
When p = 98%, z = 2.05375
Next, we calculate the x values from \mathbf{z= \frac{x - \mu}{\sigma}}z=
σ
x−μ
Substitute \mathbf{z = -2.32635}z=−2.32635
\mathbf{-2.32635 = \frac{x - 63.5}{2.5}}−2.32635=
2.5
x−63.5
Multiply through by 2.5
\mathbf{-2.32635 \times 2.5= x - 63.5}−2.32635×2.5=x−63.5
Make x the subject
\mathbf{x = -2.32635 \times 2.5 + 63.5}x=−2.32635×2.5+63.5
\mathbf{x = 57.684125}x=57.684125
Approximate
\mathbf{x = 57.7}x=57.7
Similarly, substitute \mathbf{z = 2.05375}z=2.05375 in \mathbf{z= \frac{x - \mu}{\sigma}}z=
σ
x−μ
\mathbf{2.05375= \frac{x - 63.5}{2.5}}2.05375=
2.5
x−63.5
Multiply through by 2.5
\mathbf{2.05375\times 2.5= x - 63.5}2.05375×2.5=x−63.5
Make x the subject
\mathbf{x= 2.05375\times 2.5 + 63.5}x=2.05375×2.5+63.5
\mathbf{x= 68.634375}x=68.634375
Approximate
\mathbf{x= 68.6}x=68.6
Hence, the new height requirements would be 57.7 to 68.6 inches
Write the first four terms of the sequence whose nth term is given by the formula.
an = n − 5/n
a1 =
a2 =
a3 =
a4 = .
Answers
a(2) = 2 - 5/2 = -0.5
a(3) = 3 - 5/3 = 1.333
a(4) = 4 - 5/4 = 2.75
just plug in each term number to n
Find the inverse of A = 9, -2 -10, 7 , if it exists.
Answers
The inverse of matrix A, if it exists, is:
A^(-1) = [7/43, 2/43; 10/43, 9/43]
To find the inverse of a matrix A, we need to determine if the matrix is invertible by calculating its determinant. If the determinant is non-zero, then the matrix has an inverse.
Given the matrix A = [9, -2; -10, 7], we can calculate its determinant as follows:
det(A) = (9 * 7) - (-2 * -10)
= 63 - 20
= 43
Since the determinant is non-zero (43 ≠ 0), we can proceed to find the inverse of matrix A.
The formula to calculate the inverse of a 2x2 matrix is:
A^(-1) = (1/det(A)) * [d, -b; -c, a]
Plugging in the values from matrix A and the determinant, we have:
A^(-1) = (1/43) * [7, 2; 10, 9]
Simplifying further, we get:
A^(-1) = [7/43, 2/43; 10/43, 9/43].
For more such questions on Inverse of matrix:
https://brainly.com/question/27924478
#SPJ8
Which arrangement shows 27/5, 5.36, 5 3/5, 33/6 in order from least to greatest?
Answers
Answer:
5.36 < 27/5 < 33/6 < 5 3/5 or 5.36, 27/5, 33/6, 5 3/5
Step-by-step explanation:
hay 1230 personas, entre hombres y mujeres. Si se sabe que el número de mujeres, supera en 150 al número de hombres. ¿Cuántos hombres están habitando la mini ciudad?
Answers
There are 540 men living in the mini city.
x + (x + 150) = 1230
Simplifying this equation, we get:
2x + 150 = 1230
Subtracting 150 from both sides, we get:
2x = 1080
Dividing both sides by 2, we get:
x = 540
Therefore, there are 540 men living in the mini city.
To check our answer, we can substitute x = 540 into our original equation:
540 + (540 + 150) = 1230
690 = 1230
This is false, so there must be an error in our calculation. We can double-check our work by trying a different approach.
We know that the number of women exceeds the number of men by 150, so we can represent the number of women as (x + 150). We also know that the total number of people is 1230, so we can set up an equation:
x + (x + 150) = 1230
Simplifying this equation, we get:
2x + 150 = 1230
Subtracting 150 from both sides, we get:
2x = 1080
Dividing both sides by 2, we get:
x = 540
For such more questions on mini
https://brainly.com/question/29266607
#SPJ8
The fence around Wayne Manor is going to be replaced. No fence will be required on the side lying along Gotham River. If the new wrought iron fence costs $12 per meter for the side parallel to the river, and $4 per meter for the other two sides, find the dimensions of the maximum area that can be enclosed by the fence if Bruce Wayne cannot spend more than $3600.
Answers
Step-by-step explanation:
Let the side parallel to the river be x meter and the other two sides be of y meter, then
\(12 x+(2 y)(4)=3600\)
\(12 x+8 y &=3600\)
\(3 x+2 y &=900\)
\(2 y &=900-3 x\)
The area of the rectangle is \(A=xy \)
Substitute into to express the area in a single variable x as,
\(A(x) &=x\left[\frac{1}{2}(900-3 x)\right]\)
\(=\frac{1}{2}\left(900 x-3 x^{2}\right)\)
Differentiate A(x) with respect to x and equate to zero as,
\(A^{\prime}(x) &=0\)
\(\frac{d}{d x}\left[\frac{1}{2}\left(900 x-3 x^{2}\right)\right]=0\)
\(900-3(2 x) =0\)
x=150
Here, \(A^{\prime \prime}(x)=-3 x<0\) at \(x=150 \Rightarrow A\) is maximum
Therefore, the dimension is:
Length of side parallel to the river: x=150 m.
Length of other two side: \(y=\frac{1}{2}(900-450)=225\) m.
A rectangle is 4 feet longer than it is wide. If the area of the rectangle must be less than or equal to 672 square feet, find the possible values for the width .
Answers
The possible values for the width of rectangle are 24 and -28.
What is area of rectangle?
The area of a rectangle formula. Area of a Rectangle is A = l × b. Once the length and width of a rectangle are known, the area can be calculated. The area of the rectangle is calculated as a square unit by multiplying the length and width.
Let x is the width of rectangle.
As given a rectangle length is 4 feet longer than it is wide.
⇒ l = 4 + x
Since,
Area of rectangle = length x width
672 = (4 + x) x x
672 = 4x + x^2
x^2 + 4x - 627 = 0
To find the value of x we can use the quadratic formula.
Here a = 1, b = 4, c = -672
\(x = \frac{-b +-\sqrt{b^2-4ac} }{2a} \\x = \frac{-4+-\sqrt{4^2-4(1)(-672)} }{2(1)} \\x = \frac{-4+-\sqrt{2704} }{2} \\x = \frac{-4+-52}{2} \\x = -2+-26\)
⇒ x = -2 + 26, x = -2 - 26
⇒ x = 24, x = -28
Hence, the possible values for the width of rectangle are 24 and -28.
To know more about area of rectangle, click on the link
https://brainly.com/question/2607596
#SPJ4
What is the slope of a line that is parallel to the line y=3/4x+2?

Answers
Answer:
C)
Step-by-step explanation:
The line is in the form of y = ax + b, which (a) part is just the slope, so the slope is 3/4.
Answer:
3/4
Step-by-step explanation:
Y=mx+b
Which values of a, b, and c correctly represent the answer in simplest form? 3 =a O a=38.0= 14.0=1 a=1.0= 14.C = 38 O a= 1.5=7.C= 19 O a = 19.0= 7.0= 1
Answers
Answer:
The answer could be A) or D) because the zero acts as a place holder. Its a little easier to derive it if you have a bigger decimal
Step-by-step explanation:
A group of people were asked if they had run a red light in the last year. 363 responded "yes", and 138
responded "no".
Find the probability that if a person is chosen at random, they have run a red light in the last year.
Answers
Answer:
363/501
Step-by-step explanation:
363+138=501.........
Suppose it takes 18 hours for a pipe to fill a tank of water, if the tank
had no leak. However, our tank has a crack that will cause a full tank to
leak out in 30 hours. If the tank starts off empty, how long will it take to
fill the leaky tank?
Answers
Answer:
Step-by-step explanation:
Let the volume of tank be x
In 18 hours volume of tank filled = x
we have to find the volume of tank which is filled in 1 hours.
For that we divide LHS and RHS by 18
In 18/18 hours volume of tank filled = x/18
In 1 hours volume of tank filled = x/18
In 30 hours volume of tank emptied = x
we have to find the volume of tank which is emptied in 1 hours.
For that we divide LHS and RHS by 30
in 30/30 hours volume of tank filled = x/30
In 1 hours volume of tank filled = x/30
If tank is empty and one starts to fill it, two things will happen
it will start filling at rate of x/18 hours
But there is leak which will start to empty the tank at x/30 hours
So , at any given time rate if filling of water will be rate of filling the tank- rate of emptying the tank
In 1 hour volume of tank filled if both filling and leaking takes place simultaneously = x/18 -x/30 = (30-18)x/18*30 = 12x/18*30 = x/3*15 = x/45
In 1 hour volume of tank filled = x/45
in 1*45 hour volume of tank filled = x/45*45 = x
Thus, it will take 45 hours to fill the leaky tank .
According to the diagram, a 13-foot ladder leans against a 12-foot wall. The distance from the base of the wall is 5 feet. Based on this information, which trigonometric ratio has the value of 12/5
Answers
Answer:
Tangent
Step-by-step explanation:
if the angle in question is the bottom of the ladder and the ground, then tangent is opposite over adjacent... or 12/5
Hope this is right
helppppppppp i m on my test

Answers
-75 -75
3x=105
3x/3= 105/3
x=35
*Brainly* Find the equation of the line shown in the graph. Write the equation in slope-intercept form.
If you give an explanation I'll thank you!

Answers
Answer:
y = (-4/3)x + 6
Step-by-step explanation:
The Y-intercept of the graph is 6. You can find the slope by following rise over run, or the change in y divided by the change in x. From (0,6) to (3,2), there is a negative 4 change in y and positive 3 change in x.
what is the answer? pls help

Answers
Answer:
\(\frac{3}{2}\)
Step-by-step explanation:
For this, we shall use the slope formula:
\(\frac{y_2 - y_1}{x_2 - x_1}\) ← this is \(\frac{rise}{run}\)
Assuming this is a line, all we do is pick two consecutive points and plug them in. For example, let's take the first two points. (1, -4) and (7, 5) as they are the easiest to work with.
Let's plug in these two values:
\(\frac{5 - (-4)}{7 - 1}\)
Simplified we get:
\(\frac{9}{6}\)
We are now able to factor 3 out of the numerator and denominator:
\(\frac{3}{2}\)
Thus resulting in the slope.
A
-6
Find the distance, d, of AB.
A = (-5, 5) B = (5, -5)
-4 -2
f
&
-2
-4
9
N
4
B
d = √|×₂ − ×₁1² + y2 - Y₁|²
d = [?]
Round to the nearest tenth.
Distance
Enter
Answers
Answer:
88
Step-by-step explanation:
What is the length of EF in the right triangle below?
D
26
10
E
F
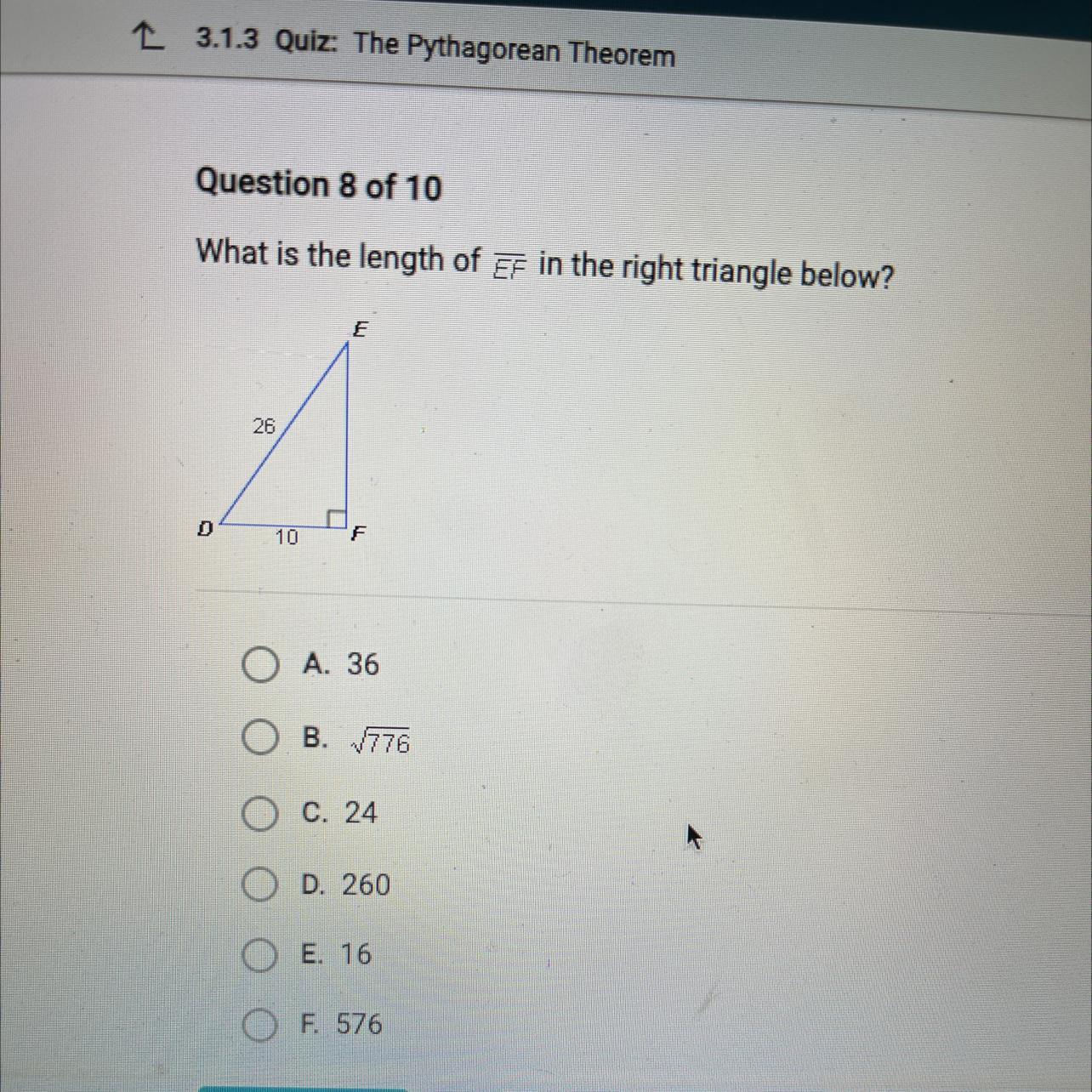
Answers
The measure of side length EF in the right triangle is 24.
What is the measure of side length EF?The Pythagorean theorem states that the "square on the hypotenuse of a right-angled triangle is equal in area to the sum of the squares on the other two sides.
It is expressed as;
c² = a² + b²
From the diagram:
Hypotenuse DE = c = 26
Leg DF = a = 10
Leg EF = b = ?
Plug in the values and solve for b:
c² = a² + b²
26² = 10² + b²
676 = 100 + b²
b² = 676 - 100
b² = 576
b = +√576 ( we take the positive value since we are dealing with dimensions)
b = 24
Therefore, the length EF is 24.
Option C)24 is the correct answer.
Learn more about Pythagorean theorem here: brainly.com/question/343682
#SPJ1
Consider the function represented by this graph.
What is the domain of this function?
A. {x|x ≥0}
B. {x|x ≤8}
C. {x|0 ≤x ≤8}
D. {x|x ≤0x ≥8}

Answers
Remember that
For a pair (x,y)
x is domain and y is rangeSo here
The end points
(0,9)(8,1)Hence domain
0≤x≤8Option C
What is the value of y?

Answers
Answer:
Step-by-step explanation:
Remark
The value of the y can be found by using the Geometric Mean. To use the said mean, you must compare parts of one triangle to parts of the second triangle. In this case, the small triangle containing boy 4 and y, must be compared to the triangle use y and 12
Formula
This translates to
4 / y = y/12
Explanation. The two triangles y and 4 and y and 12 are similar. The short side on the small right triangle on the left is 4. The second longest side on the same triangle is y.
In the triangle containing y and 12 The short side is y and the second side length is 12. You have to read this a couple of times to get the meaning of the two ratios.
Solution
4/y = y / 12 Cross multiply
y^2 = 4 * 12
y^2 = 48 Take the square root of both sides.
√y^2 = √48
y = √2 * 2 * 2 * 2 * 3
y = 2 * 2 * √3
Answer
y = 4√3
Answer:
y = 4√3 y = 4√3
Step-by-step explanation:
i hope it's help
Given the geometric sequence an with the following information, find a7.

Answers
To find the value of Az in the geometric sequence, we can use the given information. The geometric sequence is represented as follows: A3, 60, 160, 06 = 9.
From this, we can see that the third term (A3) is 60 and the common ratio (r) is 160/60.
To find Az, we need to determine the value of the nth term in the sequence. In this case, we are looking for the term with the value 9.
We can use the formula for the nth term of a geometric sequence:
An = A1 * r^(n-1)
In this formula, An represents the nth term, A1 is the first term, r is the common ratio, and n is the position of the term we are trying to find.
Since we know A3 and the common ratio, we can substitute these values into the formula:
60 =\(A1 * (160/60)^(3-1)\)
Simplifying this equation, we have:
\(60 = A1 * (8/3)^260 = A1 * (64/9)\)
To isolate A1, we divide both sides of the equation by (64/9):
A1 = 60 / (64/9)
Simplifying further, we have:
A1 = 540/64 = 67.5/8.
Therefore, the first term of the sequence (A1) is 67.5/8.
Now that we know A1 and the common ratio, we can find Az using the formula:
Az = A1 * r^(z-1)
Substituting the values, we have:
Az =\((67.5/8) * (160/60)^(z-1)\)
However, we now have the formula to calculate it once we know the position z in the sequence.
For more such questions on geometric sequence
https://brainly.com/question/24643676
#SPJ8
Use ALL of the tools have, to find area and perimeter of this below:

Answers
9514 1404 393
Answer:
area 36 ft²perimeter 30 ftStep-by-step explanation:
The area can be decomposed into a rectangle and a trapezoid.
The rectangle is 2' by 5', so has area ...
A = LW
A = (5 ft)(2 ft) = 10 ft²
The trapezoid has bases 8 ft and 5 ft, and height 4 ft, so its area is ...
A = 1/2(b1 +b2)h
A = 1/2(8 ft +5 ft)(4 ft) = 26 ft²
Then the total area of the figure is ...
total area = 10 ft² +26 ft² = 36 ft²
__
The slant side of the trapezoid is the hypotenuse of a triangle with sides 3 and 4. The Pythagorean theorem tells us its length is ...
c = √(a² +b²) = √(3² +4²) = √25 = 5
The perimeter of the figure is the sum of the side lengths. Working clockwise from the top, that sum is ...
P = 5 + 4 + 2 + 2 + 5 + 2 + 5 + 5 = 30 . . . feet
The perimeter of the figure is 30 feet.

My checking account balance was $443 on February 1st and $872 on February 7th. Show the rate of change
Answers
Answer:
$61.29 per day.
Step-by-step explanation:
Checking account balance on February 1st: $443
Checking account balance on February 7th: $872
Difference in balances: $872 - $443 = $429
Number of days between February 1st and February 7th: 7 days
Rate of change = Difference in balances / Number of days
Rate of change = $429 / 7 days
To find the rate of change per day, divide the difference in balances by the number of days:
Rate of change = $429 / 7 days ≈ $61.29 per day
Therefore, the rate of change in your checking account balance during that period was approximately $61.29 per day.