A brewery distributes beer in cans labeled 12 oz. The Bureau of Weights and Measures randomly selects 36 cans, measures their contents, and obtains a sample mean of 11.82 oz. Assume that σ is known to be 0.38 oz. At 0.01 significance level, can we conclude that the brewery is cheating consumers? Please show all 4 steps of the classical approach clearly.
Answers
Answer:
Hypothesis
Null hypothesis:\(\mu = 12\)
Alternative hypothesis:\(\mu \neq 12\)
Statistic
\(t=\frac{11.82-12}{\frac{0.38}{\sqrt{36}}}=-2.84\)
\(df=n-1=36-1=35\)
P value
The p value for this case would be given by:
\(p_v =2*P(t_{(35)}<-2.84)=0.0075\)
Conclusion
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis and we can conclude that the true mean is significantly different from 12 oz.
Step-by-step explanation:
Information given
\(\bar X=11.82\) represent the sample mean
\(s=0.38\) represent the sample standard deviation
\(n=36\) sample size
\(\mu_o =12\) represent the value to verify
\(\alpha=0.01\) represent the significance level
t would represent the statistic
\(p_v\) represent the p value for the test
Hypothesis to verify
We want to cehck if the true mean is 12 or not, the system of hypothesis would be:
Null hypothesis:\(\mu = 12\)
Alternative hypothesis:\(\mu \neq 12\)
Statistic
The statistic is given by:
\(t=\frac{\bar X-\mu_o}{\frac{s}{\sqrt{n}}}\) (1)
Replacing the info given we got:
\(t=\frac{11.82-12}{\frac{0.38}{\sqrt{36}}}=-2.84\)
The degrees of freedom are given by:
\(df=n-1=36-1=35\)
P value
The p value for this case would be given by:
\(p_v =2*P(t_{(35)}<-2.84)=0.0075\)
Conclusion
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis and we can conclude that the true mean is significantly different from 12 oz.
Related Questions
An increase from $27 to $35.10 what percent of increase?
Answers
Answer:
30% increase
Step-by-step explanation:
percentage increase is calculated as
\(\frac{increase}{original}\) × 100%
increase = $35.10 - $27 = $8.10 , then
percentage increase = \(\frac{8.10}{27}\) × 100% = 0.3 × 100% = 30%
Answer:
Step-by-step explanation:
step 1: 35.10-27 =8.1
step 2: 8.1/27 x 100 = 30%
so therefore = 30% increase
Select all the transformations of f(x) = x2 that combine to result in the graph of function g below. A parabola with vertex negative 1 comma negative 2 that opens downward. The graph passes through the points negative 3 comma negative 3 and 1 comma negative 3. Group of answer choices reflection across the x-axis translation of 2 units down translation of 1 unit left translation of 2 units up vertical stretch by a factor of 2 horizontal stretch by a factor of 2 translation of 1 unit right

Answers
Answer:
Step-by-step explanation:
Equation of a parabola is represented by,
f(x) = -a(x - h)² + k [Parabola opening downwards]
where (h, k) is the vertex of the parabola.
Picture attached shows the vertex as (-1, -2)
Therefore, equation of the transformed parabola will be,
f(x) = -a(x + 1)²- 2
Since the given parabola passes through a point (1, -3)
-3 = -a(1 + 1)² - 2
-1 = -4a²
a = \(\sqrt{\frac{1}{4} }\)
a = \(\frac{1}{2}\)
Therefore, equation of the transformed function will be,
f(x) = \(-\frac{1}{2}(a+1)^2-2\)
If the original or parent function is g(x) = x²,
Transformed function will have the following characteristics,
1). Function will have vertex as (-1, -2) opening downwards.
2). Graph passes through (-3, -3) and (1, -3).
3). Reflection across x-axis.
4). Translation of 2 units down and 1 unit to the left.
5). Horizontal stretch by a factor of 2.
Using translation concepts, it is found that these following transformations happened:
Reflection across the x-axis.Translation of 1 unit left.Translation of 2 units down.The parent function \(y = x^2\) points upward and has vertex at (0,0).
In the graph, the parabola points downward, so it was reflected across the x-axis.The x-coordinate of the vertex of the shifted function is -1, thus it was translated 1 unit to left.The y-coordinate of the vertex of the shifted function is -2, thus it was translated 2 units down.A similar problem is given at https://brainly.com/question/4521517
Solve the equation below for x.
cx-4=7
A. x=c/3
B. x=3/c
C. x=11/c
D. x=c/11
Answers
Answer:
x = 11/c
Step-by-step explanation:
Solve for x:
c x - 4 = 7
Hint: | Isolate terms with x to the left-hand side.
Add 4 to both sides:
c x = 11
Hint: | Solve for x.
Divide both sides by c:
Answer: x = 11/c
Find the median of the data in the box plot below. PLEASE HELP

Answers
2,4,6,8,10
6 is in the middle
Given:
What’s the statement and reasons
Answers
The statement and reasons are
1. AB ≅ BC, AE ≅ FC 1. Given2. AC ≅ AC 2. Reflexive property of congruence3. <BAC ≅ <BCA 3. Base angles of isosceles ∆BAC4. ∆AEC ≅ ∆AFC. 4. SAS5. <AEC ≅ <AFC. 5. CPCTCHow to determine the proof of the trianglesThe complete question is added as an attachment
With the given information and the image attached below, we can state that the two triangles are congruent by SAS,
Then go ahead to use the CPCTC to show that any of their corresponding parts are congruent as well.
Part of the proof is as follows:
Statement Reason
1. AB ≅ BC, AE ≅ FC 1. Given
2. AC ≅ AC 2. Reflexive property of congruence
Read more about congruence proof at:
brainly.com/question/2102943
#SPJ1

Help!!! Asap!! Will give out brainliest!! Need to explain how you did it please and thanks!! Just look at the picture attached!! Thank you so much!!
9) Which piecewise function is shown on the graph?
8
[485 - 5, ICO
f(3) = 3 0 SI56
-- - 7, I>6
6
2
(-4e5 – 5, I<0
(*) = 3
03:36
|-+7 >6
.
>
2
-6
-3
(465 - 5, ICO
0 SI56
1-5+7,> 6
(ges + 5, sco
f(1) = 3
0 SI56
= + 7
I>6

Answers
9514 1404 393
Answer:
C f(x) = {4e^x -5, ..., -x +7, ...
Step-by-step explanation:
The easiest portion to check is the constant section in the interval [0, 6]. All of the function definitions agree on that, so that doesn't help choose the right answer.
__
Next easiest is the linear section at the right. It has a negative slope. Extension of the line to the y-axis shows it has a positive y-intercept. This eliminates choices A and D.
__
The horizontal asymptote of the exponential portion at the left is -5. Both of the remaining choices B and C agree on that. The exponential is increasing at an increasing rate, so its coefficient is positive. This eliminates choice B.
The appropriate description of the function on the graph is offered by choice C.
_____
The graph below plots the function. We note that the given graph seems to show the exponential curve incorrectly.

use the shell method to find the volume generated by revolving the shaded regions bounded by the curves and lines in exerciss 7-12about the y-axis
Answers
The answer is 1) V = \(2\pi\int\limits(2)+ {x} \, dx\); 2) V = \(2\pi \int\limits(1 - 2x) - 2x dx\); 3) V =\(2\pi \int\limits {\sqrt{2} } \, dx\) ; 4) V = \(2\pi\int\limits {\sqrt{(-2/2)(2-2)} \ dx\) .
1) The volume of the shell is then given by the product of the area of its curved surface and its height. The height is equal to 2 - (-2) = 4, and the radius is equal to the minimum of the distances from x = 2 to the two curves, which is x = 2 - () = 2 + . The volume of the solid is then given by the definite integral:
V = \(2\pi\int\limits(2)+ {x} \, dx\) = \(2\pi [(/3) + 2x]\) evaluated from 0 to 1 = (4/3)π.
2) The height of the region is equal to - (2x) = -2x, and the radius is equal to the minimum of the distances from x = 1 to the two curves, which is x = 1 - (2x) = 1 - 2x. The volume of the solid is then given by:
V = \(2\pi \int\limits(1 - 2x) - 2x dx\)=\(2\pi [/5 - 2/3 + /2]\) evaluated from 0 to 1 = (8π/15).
3) The height of the region is equal to (2-x) - = 2-x. The radius is equal to the minimum of the distances from x = 0 to the two curves, which is x = The volume of the solid is then given by:
V =\(2\pi \int\limits {\sqrt{2} } \, dx\) = \(2\pi [(x^4/4)]\) evaluated from 0 to √2 = (π/2).
4) The height of the region is equal to () - (2-) = 2 - 2. The radius is equal to the minimum of the distances from x = 0 to the two curves, which is x = √((2-)/2). The volume of the solid is then given by:
V = \(2\pi\int\limits {\sqrt{(-2/2)(2-2)} \ dx\) = \(4\pi [(2/3)\± (2\sqrt{2} /3)]\)
The complete Question is:
Use the shell method to find the volumes of the solids generated by revolving the regions bounded by the curves and lines in about the
1. y = x, y = -x/2, and x = 2
2. y = 2x, y = x/2, and x = 1
3. y = x/2, y = 2-x, and x = 0
4. y = 2-x/2, y = x/2, and x = 0
To know more about Shell Methods:
brainly.com/question/17074517
#SPJ4
Peter borrowed $100,000 at 8% compounded
annually, how much will he be paying after 2
years?
Answers
Answer:
The general formula for this type of problem is F=P[1+(i/n)]^(nt), where F is the Future Worth, P is Present Worth, i is interest, n=1 for annual payments, and t for the number of periods - which is 2. This is solved as: F=100000[1+(0.08/1)]^(1*2)=116640
Step-by-step explanation:
please help
What is the distance to the earth’s horizon from point P?
Enter your answer as a decimal in the box. Round only your final answer to the nearest tenth.
x =
mi

Answers
The measure of distance x, that is, the distance between a point P and the point of horizon, is equal to 284.372 miles.
How to find the distance to the earth horizon from a given point
In this problem we must determine the distance between a point P located about earth's circumference and the point of horizon, located on earth's circumference. Since the line between these two points is tangent to earth, then, distance x can be found by Pythagorean theorem:
x = √[(3959 mi + 10.2 mi)² - (3959 mi)²]
x = 284.372 mi
The distance x is equal to 284.372 miles.
To learn more on Pythagorean theorem: https://brainly.com/question/14930619
#SPJ1
What is the vertex for the graph below ? 10 A . (- 2, 0) B . (0, - 2) . (2, 0) D . (0, 2)
Answers
The vertex for the graph is at (2, 0).
What is a parabola?A parabola is formed by cutting a right circular cone in half along a plane perpendicular to the cone's generator. It is a locus of a moving point whose separation from the focus is equal to its separation from a stationary line (directrix)
Focus is a fixed point.
Directrix is the name for fixed lines.
Given the graph is a parabola,
A parabola's vertex is the location where its symmetry line and parabola intersect. The vertices of a parabola whose equation is provided in standard form will be the lowest (lowest point) and highest (highest point) points on the graph, respectively.
The minimum point in graph is (2, 0)
Hence vertex is (2, 0).
learn more about parabola;
https://brainly.com/question/21685473
#SPJ1
The complete question is in image,

what should be added to 7 3/5 to get 18 (Step explanation )
Answers

Wei has 150.00 to make a garland using 60-cent balloons
Answers
Answer:
The answer is 0.60b + 0.30w = 150; 60 + 0.30w = 150
Step-by-step explanation:
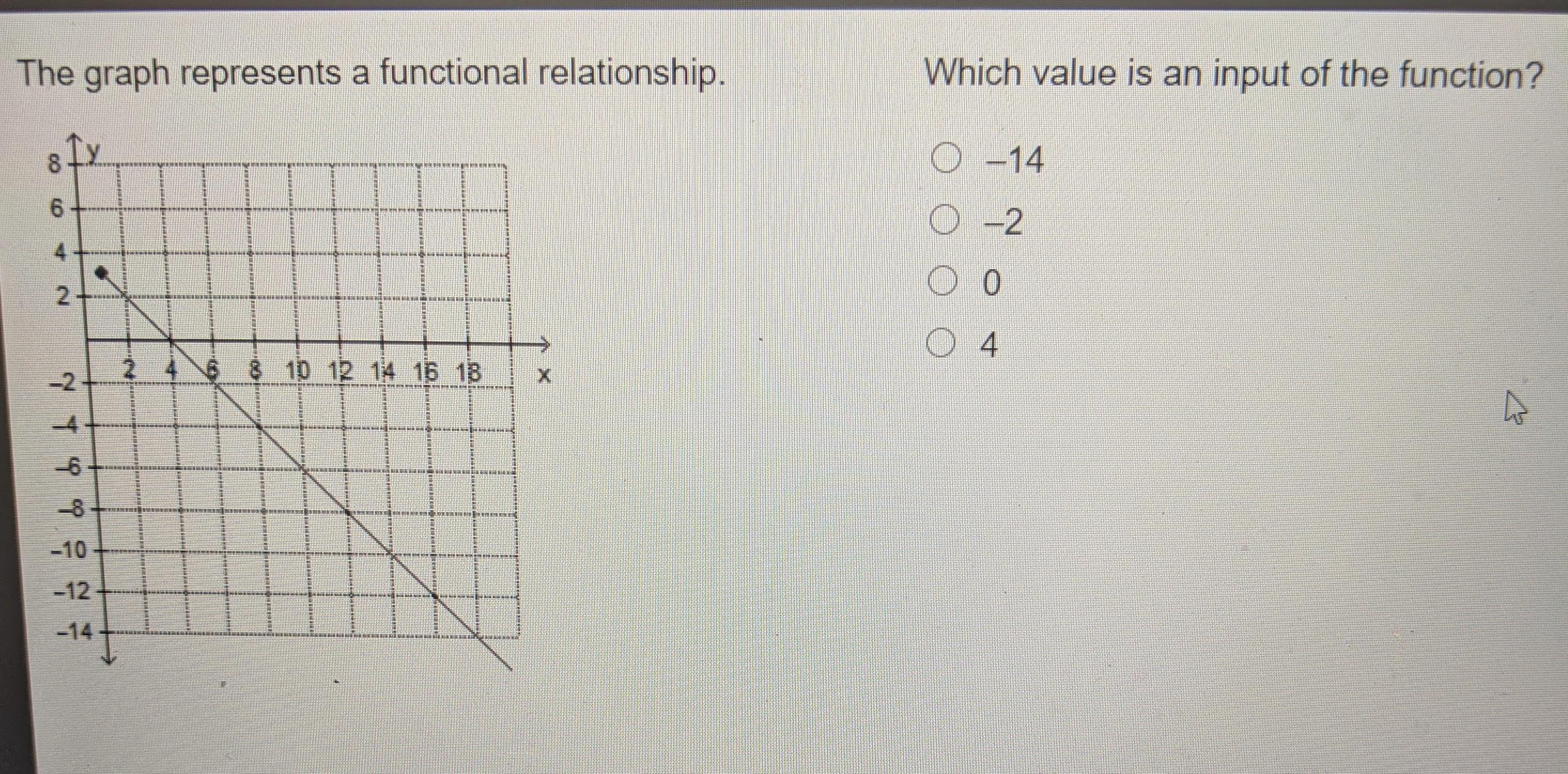
The graph represents a functional relationship. (View Graph) Which value is an input of the function? -14 -2 0 4
Answers
Answer:
4
Step-by-step explanation:
The horizontal extent of the function is x ≥ 1. These are the input values. The function is not defined for negative input values or for x=0.
Of the given choices, the function is only defined for the input x = 4.
Answer:
D. 4
Step-by-step explanation:
Point A’ is the image of Point A when point A is rotated about the origin B. What angle in the counterclockwise direction is A rotated through?

Answers
Answer:
90 degrees
Step-by-step explanation:
A survey of 800 randomly selected adults in a certain country found that 82% believed that
protecting the rights of those with unpopular views is a very important component of a strong
democracy.
a. Verify the Central Limit Theorem conditions.
b. Find a 95% confidence interval for the proportion of adults in the country who believe that
protecting the rights of those with unpopular views is a very important component of a strong
democracy.
c. Would a 90% confidence interval based on this sample be wider or narrower than the 95%
interval? Give a reason for your answer.
Answers
a) the Central Limit Theorem conditions are met. b) The 95% confidence interval for the proportion of adults who believe in protecting the rights of those with unpopular views is approximately 0.7934 to 0.8466.
c) . A 90% confidence interval would be wider than the 95% interval
How to Verify the Central Limit Theorem conditions.To verify the Central Limit Theorem (CLT) conditions, we need to check the following:
1. Random Sampling: The survey states that 800 adults were randomly selected, which satisfies this condition.
2. Independence: We assume that the responses of one adult do not influence the responses of others. This condition is met if the sample is collected using a proper random sampling method.
3. Sample Size: To apply the CLT, the sample size should be sufficiently large. While there is no exact threshold, a common rule of thumb is that the sample size should be at least 30. In this case, the sample size is 800, which is more than sufficient.
Therefore, the Central Limit Theorem conditions are met.
b. To find a 95% confidence interval for the proportion of adults who believe in protecting the rights of those with unpopular views, we can use the formula for calculating a confidence interval for a proportion:
CI = p ± z * √(p(1-p)/n)
where:
- p is the sample proportion (82% or 0.82 in decimal form).
- z is the z-score corresponding to the desired confidence level. For a 95% confidence level, the z-score is approximately 1.96.
- n is the sample size (800).
Calculating the confidence interval:
CI = 0.82 ± 1.96 * √(0.82(1-0.82)/800)
CI = 0.82 ± 1.96 * √(0.82*0.18/800)
CI = 0.82 ± 1.96 * √(0.1476/800)
CI = 0.82 ± 1.96 * √0.0001845
CI ≈ 0.82 ± 1.96 * 0.01358
CI ≈ 0.82 ± 0.0266
The 95% confidence interval for the proportion of adults who believe in protecting the rights of those with unpopular views is approximately 0.7934 to 0.8466.
c. A 90% confidence interval would be wider than the 95% interval. The reason is that as we increase the confidence level, we need to account for a larger margin of error to be more certain about the interval capturing the true population proportion. As a result, the interval needs to be wider to provide a higher level of confidence.
Learn more about confidence interval at https://brainly.com/question/73194
#SPJ1
The function G(m) = 49.5m + 89.75 represents the cost of joining the gym in addition to the one time membership fee. The cost, G, is measured in dollars for m months. 1. Find the value of G(6).
Answers
Answer:
386.75
Step-by-step explanation:
added in the picture
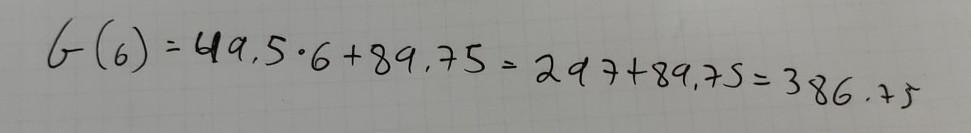
The cost of joining the gym for 6 months is 386.75.
Given,
The function G(m) = 49.5m + 89.75 represents the cost of joining the gym in addition to the one-time membership fee.
The cost, G, is measured in dollars for m months.
We need to find the value of G(6).
Here,
The one-time membership = 89.75.
Now,
Putting m = 6 months in:
G(m) = 49.5m + 89.75
G(6) = 49.5 x 6 + 89.75
= 297 + 89.75
= 386.75
Thus the cost of joining the gym for 6 months is G(6) = 386.75.
Learn more about finding the value of a function here:
https://brainly.com/question/8822000
#SPJ2
Amit sold 3 shells last week for $5 each
and 2 more shells this week for $5 each.
Show two ways to determine how much
money Amit made in the two weeks.
Answers
The two ways to determine how much money Amit made in the two weeks are,
$5(3 + 2) = $25 and $5(3) + $5(2) = $25.
What is shell?
A hard, protective outer layer is typically produced by an animal that lives in the sea and is referred to as a shell, seashell, or simply a shell. The animal's body includes the shell. Beachcombers regularly discover empty seashells washed up on beaches.
Given: Amit sold 3 shells last week for $5 each.
And 2 more shells this week for $5 each.
So, the equation which represent the total money is,
$5(3) + $5(2) = $15 + $10 = $25.
Also we can express this equation as,
$5(3 + 2) = $5(5) = $25
Therefore, the two ways to determine how much money Amit made in the two weeks are,
$5(3 + 2) = $25 and $5(3) + $5(2) = $25
To know more about the shells, click on the link
https://brainly.com/question/26039758
#SPJ9
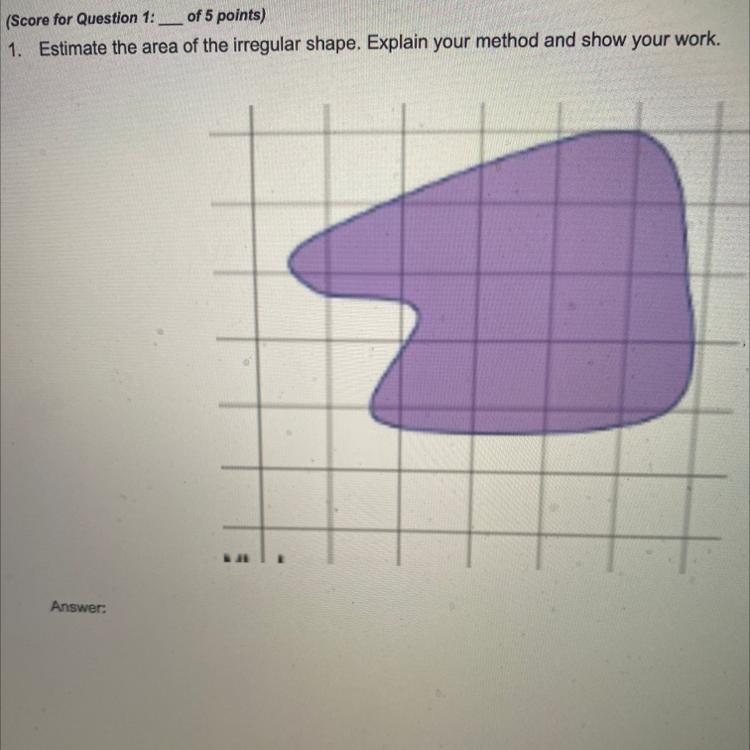
1. Estimate the area of the irregular shape. Explain your method and show your work.
Answers
Check the picture below.
so each row has a few gaps, but also has a few surplusses, so we can use the surplusses to fill up the gaps, and that will give us more or less 3 + 5 + 4 + 4 units, namekly 16 units.

WILL GIVE BRAINLIEST FOR THE CORRECT ANSWER!!
What scale factor was applied to the first rectangle to get the resulting image?
Enter your answer as a decimal in the box.

Answers
Answer:
2.5
Step-by-step explanation:
the length has increased by 7.5/3 = 2.5.
so the scale factor is 2.5
HELP LOOK AT PHOTO PLEASE

Answers
Answer:
y=60
Step-by-step explanation:
1) Find x
All the interior angles of a triangle add up to 180 degrees. Knowing this, we can construct the following equation:
\(180=x+35+25\\180=x+60\)
Subtract 60 from both sides
\(180-60=x+60-60\\120=x\)
2) Find y
A straight line has an angle measure of 180 degrees as well. Knowing this, we can construct the following equation:
\(180=x+y\\180=120+y\)
Subtract 120 from both sides of the equation
\(180-120=y+120-120\\60=y\)
There is also a second way to solve for y: An exterior angle of a triangle is equal to the sum of the opposite interior angles. y, in this case, would be the exterior angle and 35 and 25 degrees would measure the opposite interior angles. To solve for y, we just add 35 and 25, getting us 60 degrees.
I hope this helps!
this distance between two floors is 9'0 1/2". if 14 raisers are to be used in a set of stairs, what is the height of each raiser?
Answers
If the total height between two floors is 9'0 1/2" and 14 risers are to be used in a set of stairs, the height of each riser would be approximately 7.75 inches.
To find the height of each riser in a set of stairs given the total height between two floors, we need to divide the total height by the number of risers.
First, let's convert the total height to a consistent unit. The distance between two floors is given as 9'0 1/2". We can convert this to inches by multiplying the feet by 12 and adding the remaining inches:
9 feet = 9 * 12 = 108 inches
0 1/2 inch = 0.5 inch
Total height = 108 + 0.5 = 108.5 inches
Next, we divide the total height by the number of risers (14) to find the height of each riser:
Height of each riser = Total height / Number of risers
Height of each riser = 108.5 inches / 14
Using a calculator, we can compute:
Height of each riser ≈ 7.75 inches
Therefore, the height of each riser in the set of stairs would be approximately 7.75 inches.
For more such question on height. visit :
https://brainly.com/question/28990670
#SPJ8
PLEASE HELP DUE SOON! PLEASE SHOW WORK SO I KNOW HOW TO IT FOR NEXT TIME! IM STUCK ON THIS AND ITS DUE TODAY!!!!! YOU WILL GETT 100 POINTS REAL ANSWERS ONLY! MANY THANKS! QUESTIONS DOWN BELOW!!!!!

Answers
Answer:
a) zero triangles.
b) one triangle.
Step-by-step explanation:
In triangle ABC:
A, B and C are the interior angles.a, b and c are the sides opposite the corresponding interior angles.Part (a)Given:
∠A = 51°a = 10 cmb = 28 cmLaw of Sines
\(\sf \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\)
(where A, B and C are the angles and a, b and c are the sides opposite the angles)
To determine if any triangles are possible, substitute the given values into the Law of Sines to find angle B:
\(\implies \sf \dfrac{\sin 51^{\circ}}{10}=\dfrac{\sin B}{28}\)
\(\implies \sf \sin B=\dfrac{28\sin 51^{\circ}}{10}\)
\(\implies \sf \sin B=2.176008...\)
As -1 ≤ sin B ≤ 1, there is no solution for angle B.
Therefore, zero triangles are possible.
----------------------------------------------------------------------------------
Part (b)Given:
∠C = 30°a = 24 cmc = 12 cmLaw of Sines
\(\sf \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\)
(where A, B and C are the angles and a, b and c are the sides opposite the angles)
To determine if any triangles are possible, substitute the given values into the Law of Sines to find angle A:
\(\implies \sf \dfrac{\sin A}{24}=\dfrac{\sin 30^{\circ}}{12}\)
\(\implies \sf \sin A=\dfrac{24\sin 30^{\circ}}{12}\)
\(\implies \sf \sin A=1\)
\(\implies \sf A=\sin^{-1}(1)\)
\(\implies \sf A=90^{\circ}\)
Therefore, one triangle is possible (see attachment).

Can you help me on question 15?!

Answers
Answer:
B i think
Step-by-step explanation:
Math question. Geometry

Answers
9514 1404 393
Answer:
B. 4
Step-by-step explanation:
There are a couple of ways you can look at this question.
Triangle relationships
The value of x must satisfy the requirements of the triangle inequality, and that the legs of the triangle are shorter than the hypotenuse.
(x -1) +(2x -4) > (x -1) +2 ⇒ x > 3 . . . . from UW +UV > VW
2x -4 < (x -1) +2 ⇒ x < 5 . . . . from UV < VW
The only integer strictly between 3 and 5 is ...
x = 4 . . . . . . . gives a 3-4-5 right triangle
__
Pythagorean theorem
The side lengths of this right triangle must satisfy the Pythagorean theorem:
UW² +UV² = VW²
(x -1)² +(2x -4)² = ((x -1) +2)²
x² -2x +1 +4x² -16x +16 = x² +2x +1
4x² -20x +16 = 0 . . . . . put in standard form
4(x -4)(x -1) = 0 . . . . . . .factor
Solutions are x = 4 and x = 1. Only the solution x = 4 is viable in this geometry.
x = 4
One cup of spaghetti sauce covers 2.5 cups of spaghetti noodles. How many cups of noodles will 3.5 cups cover?
Answers
Answer:
8.75 cups of noodles will be covered.
What value of c makes this polynomial a perfect square trinomial?
x² + 4x + c
Answers
Answer:
4
Step-by-step explanation:
What is the range of possible sizes for side 3.2 5.5 x?
Answers
Answer:
the range is :
10 , 74 , 78 , 102
3 , 4 , 4 , 5 , 17
1.2, 1.2 , 3.2 , 3.5 , 3.6 , 6.5 , 8.2 , 9.2
Step-by-step explanation:
What is the area of the shaded region? Round to the nearest tenth.

Answers
Answer:
The answer is 50.2cm²
Step-by-step explanation:
Area of the whole circle (the whole shape)
A= πr²
A= 3.14 x (5cm)²
A= 3.14 x 25cm
A= 78.5cm²
Area of the part in the middle (non-shaded part)
A= πr²
A= 3.14 x (3cm)²
A= 3.14 x 9cm
A= 28.26cm²
78.5cm² - 28.26cm² = 50.24cm²
Answer rounded to the nearest tenth: 50.2cm²
Hope this helps :)
write 1.86×10⁵ as an ordinary numbe
Answers
\(\boxed{\sf 186,000}\boxed\)
Answer:
186,000
Step-by-step explanation:
1. Multiply 10 to the 5th power:
\(10^{5}\) = 100,000
2. Multiply:
1.86 × 100,000 = 186,000
hope this helps :)
the area of rectangular garden is 27000m2.if the ratio of length and beradth is 10:3 findits perimeter
Answers
Given :
The area of rectangular garden is 27000m² .The ratio of length and breadth is 10 : 3 .⠀
To Find :
The perimeter of the rectangular garden.⠀
Solution :
Let us assume the length as 10x m and breadth as 3x m .
⠀
We know that,
\({ \longrightarrow{\quad \sf \pmb{ Length \times Breadth = Area_{(rectangle)}}} }\)
⠀
Now, substituting the values in the formula :
\({ \longrightarrow{\quad \sf{ 10x \times 3x = 27000 }}} \)
\({ \longrightarrow{\quad \sf{ 30 {x}^{2} = 27000 }}} \)
\({ \longrightarrow{\quad \sf{ {x}^{2} = \dfrac{27000}{30} }}} \)
\({ \longrightarrow{\quad \sf{ {x}^{2} = 900 }}} \)
\({ \longrightarrow{\quad \sf{ {x}= \sqrt{900} }}} \)
\({ \longrightarrow{\quad \bf{ {x}= 30 }}} \)
⠀
Therefore,
Length = 10x m = 10(30) m = 300 mBreadth = 3x m = 3(30) m = 90 m⠀
Now,
We know that,
\({ \longrightarrow{\quad \sf \pmb{Perimeter_{(rectangle)}=2(Length + Breadth) }} }\)
⠀
Substituting the values in the formula :
\({ \longrightarrow{\quad \sf {Perimeter_{(rectangle)}=2(300 + 90) }} }\)
\({ \longrightarrow{\quad \sf {Perimeter_{(rectangle)}=2(390) }} }\)
\({ \longrightarrow{\quad \bf \pmb {Perimeter_{(rectangle)}=780 }} }\)
⠀
Therefore,
The perimeter of the rectangular garden is 780 m .The perimeter of the rectangle whose area is 27000 m² is 780 m.
What is the perimeter of a rectangle?The perimeter of a rectangle is the determinating of all the sides of the rectangle. In the given question, we have the following parameters:
Given that:
The area of the rectangle = 27000 m²The ratio of the length and the breadth is 10: 3It implies that, if the length is 10x, the breadth is 3x
The area of a rectangle = length × breath
27000 m² = (10x) × (3x)
27000 m² = 30x²
x² = 27000/30
x² = 900
x = √900
x = 30
Now, we can say that:
The length = 10(30) = 300The breath = 3(30) = 90The perimeter of the rectangle = 2(length + breadth)
The perimeter of the rectangle = 2(300 + 90)
The perimeter of the rectangle = 780 m
Learn more about the perimeter of a rectangle here:
https://brainly.com/question/19819849
#SPJ5