A bicycle with 24 inch diameter wheels is traveling at 12 mi/h. Find the angular speed of the wheels in radians per minute.
Answers
Answer:
1056 radians/min
Step-by-step explanation:
We can convert the linear speed to inches per minute to help with finding the angular speed.
(12 mi/h) = (12 mi)(5280 ft/mi)(12 in/ft)/((1 h)(60 min/h))
= (12×5280×12/60) in/min = 12,672 in/min
Each radius-length represents 1 radian of arc of the wheel. The radius is half the diameter, 24 in/2 = 12 in, so the angular speed is ...
(12,672 in/min)/(12 in/radian) = 1056 radians/min
Related Questions
Deymarius drank 2/3 of a quart of water. Wesley drank 1/6 of a quart of water. how many quarts of water did they drink all together?
Answers
Answer:
5/6 quarts of water
Step-by-step explanation:
2/3 same as 4/6. 4/6 + 1/6 = 5/6
Give the answer and an explanation

Answers
A triangle is said to be right angle if one of the angles is 90 degrees, the value of the side x for the given right angle triangle is 50.51.
What is a triangle?A triangle is a 3-sided shape that is occasionally referred to as a triangle. There are three sides and three angles in every triangle, some of which may be the same.
The sum of all three angles inside a triangle will be 180° .
The given right-angle triangle has the following sides,
AC = Base
BC = Perpendicular
AB = Hyp.
By tan function,
Since,tanθ = Perp/Base
tan29° = 28/x
x = 50.51
Hence, "A triangle is said to be right angle if one of the angles is 90 degrees, the value of the side x for the given right angle triangle is 50.51".
For more about triangles,
https://brainly.com/question/2773823
#SPJ1
Find the measure of CD.
Round to the nearest tenth.
mCD= [?]
![Find the measure of CD.Round to the nearest tenth.mCD= [?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/3ONqcHrkHawznmToXG8P62XmgkGcvDS8.png)
Answers
Answer:
The arc CD is: 114.64°
Step-by-step explanation:
The given triangle inside the circle, we can get the trigonometric ratio such as
sin x = opposite / hypotenuse
Here:
The opposite side of angle x = 36.7/2
The hypotenuse = 21.8
Thus,
sin x = [36.7/2] / [21.8]
sin x = 18.35 / 21.8
sin x = 0.8417
x = arc sin (0.8417)
x = 57.32°
Thus, the angle formed at the center by CD is:
2 x 57.32 = 114.64°
Therefore, the arc CD is: 114.64°
Answer:
The arc CD would be 114.6°
We use- sin x = opposite / hypotenuse
In the problem the opposite side of angle x = 36.7/2 and the hypotenuse = 21.8
So:
sin x = [36.7/2] / [21.8]
sin x = 18.35 / 21.8
sin x = 0.8417
x = arc sin (0.8417)
x = 57.32°
So the angle formed at the center by CD would have to be 2 x 57.32 = 114.64°
BUT, it says to round to the nearest tenth, so the answer would therefore, the arc CD is: 114.6°
The function y=−16x2+v0x models the height of a football in feet x seconds after a player kicks it. In the equation of the function, v0 is the ball's initial velocity in feet per second. The ball hits the ground 2 seconds after the player kicks it.
What is the value of v0?
Answers
Answer:
\(\large \boxed{\sf \ \ v_0=32 \ \ }\)
Step-by-step explanation:
Hello,
The equation is
\(y=f(x)=-16x^2+v_0 \cdot x\)
The ball hits the ground 2 seconds after the player kicks it, it means that f(2)=0.
We need to find \(v_0\) such that f(2)=0.
\(f(2)=-16\cdot 2^2+v_0 \cdot 2=-64+2v_0=0\\\\\text{*** add 64 to both sides ***}\\\\2v_0=64\\\\\text{*** divide by 2 both sides ***} \\\\v_0=\dfrac{64}{2}=32\)
Hope this helps.
Do not hesitate if you need further explanation.
Thank you
Answer:
v0 = 32 ft/s
Step-by-step explanation:

The Duncan family went out for dinner. They ordered 2 meals at $7.25 each and 1
meal at $5.50. They also had 3 drinks at $1.80 each and one dessert at $4.85.
a) Write an expression to evaluate the total amount spent.
b) Evaluate the expression to find the total amount spent before tip.
Answers
Answer:
look below
Step-by-step explanation:
(7.25 * 2) + 5.50 + (3 * 1.80) + 4.85
Lets combine
(7.25 * 2) + (3 * 1.8) + 10.35
7.25 * 2 is 14.50
3 * 1.8 is 5.4
14.50 + 5.4 + 10.35
is $30.25 before tip
(Tip should be 6.05 minimum, 20% of 30.25 is 6.05)
If x = y, then x – a = y – a represents the ________ property of equality.
Answers
Answer:
Subtractive Property of equality
Step-by-step explanation:
Since x = y, When you subtract anything from x, you must do the same to y for them to stay equal.
Answer:
Subtraction property of equality
please help?? its unit rate so plz help tell me how to do it
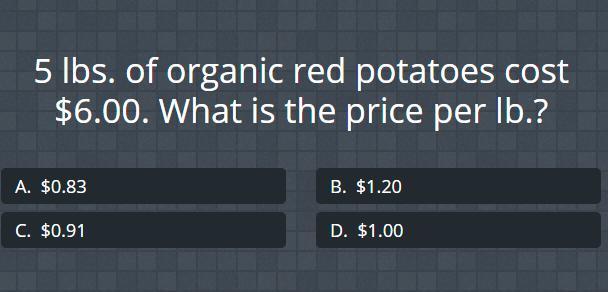
Answers
Answer:
1.2 dollars
Step-by-step explanation:
You have to divide the dollar count by the pound count.
So basically:
6/5
This gives you 1.2 dollars.
When you do unit rate, you just have to divide one value by the other value.
The value you divide by, and the value you divde, vary depending on what the question asks.
For instance, if this question asked what the pound count for 1 dollar would be, you would end up divide the 5 pounds by 6 dollars(5/6) instead of divideing the 6 dollars by 5 pounds like we did above(6/5).
Hope this helps!
Answer: 1.20 is your awnser
first divided 6.00 by 5
then you get $1.20 per pound
Step-by-step explanation:
It is expected that 30% of the criminals in our prisons are violent offenders, 65% are nonviolent, and 5% are actually innocent. A sample of 300 inmates showed that 90 were violent offenders, 200 were nonviolent, and 10 were innocent. At the .05 significance level, can we conclude that the observed frequencies are different than the expected frequencies?
Answers
Find AE. Round the answer to the nearest tenth.
A 9.7
B. 13.5
C. 16.1
D. 17.3

Answers
AE= 17.4 to nearest tenth
Step-by-step explanation:
Opposite + hypotenuse = SOH / sin
Sin 31 = 6/h
xh, then ÷ sin31
H= 6/sin31
H= 11.649....(a or b & 6 being a or b)
a^2 + b^2 = c^2
c = 13.1
Actually it's not a right-angle triangle
180 - 13+31 (or 44) = 136 degrees
Cosine rule: a^2=b^2+c^2 - 2bc cosA
AE = root 11.649...^2 + 7^2 - 2x11.649...x7xcos136
= 17.3791......
AE= 17.4 to nearest tenth
Hope this helps!
A spinner with 12 equally sized slices has 5 blue slices and 7 yellow slices. The dial is spun and stops on a slice at random. What is the probability that the dial stops on a red slice

Answers
Answer:
0
There are no red slices, so the probability is 0.
Solve the system.
-5x - 6y = -17
-3x -5y + 5z = 2
-6x - 5y + z = -13
Enter your answer as an ordered triple.
(?, ?, ?)
Answers
The value of x, y and z in the system equation is (1, 2, 3).
What is the solution of the equation?The solution of the equation can be determined by using Cramer's rule as follows;
[-5 -6 0] = [ -17]
[-3 -5 5] [2 ]
[-6 -5 1] [-13 ]
The determinant of the matrix is calculate as;
Δ = -5 (-5 + 25) + 6(-3 + 30) + 0(15 + 30)
Δ = 62
The x-determinant of the matrix is calculated as follows;
Δx = -17(-5 + 25) + 6(2 + 65) + 0
Δx = 62
The y-determinant of the matrix is calculated as follows;
Δy = -5(2 + 65) + 17(-3 + 30) + 0
Δy = 124
The z-determinant of the matrix is calculated as follows;
Δz = -5(65 + 10) + 6 (39 + 12) - 17(15 - 30)
Δz = 186
The value of x, y and z is calculated as follows;
x = Δx/Δ = 62/62 = 1
y = Δy/Δ = 124/62 = 2
z = Δz/Δ = 186/62 = 3
Learn more about system equations here: https://brainly.com/question/13729904
#SPJ1
Find the surface area and volume of a sphere.
A = 4 r²
V = 4/3r³
A sphere has a radius of 4 inches.
Area (to the nearest tenth) =
Volume (to the nearest tenth) =
sq. in.
cu. in.
Answers
\(\textit{surface area of a sphere}\\\\ SA=4\pi r^2 ~~ \begin{cases} r=radius\\[-0.5em] \hrulefill\\ r=4 \end{cases}\implies SA=4\pi (4)^2\implies SA\approx 201.1~in^2 \\\\[-0.35em] ~\dotfill\\\\ \textit{volume of a sphere}\\\\ V=\cfrac{4\pi r^3}{3}~~ \begin{cases} r=radius\\[-0.5em] \hrulefill\\ r=4 \end{cases}\implies V=\cfrac{4\pi (4)^3}{3}\implies V\approx 268.1~in^3\)
PLEASE ANSWER ASASP FOR BRAINLEST!!!!!!!!!!!!!!

Answers
Answer:
48 units squared
Step-by-step explanation:
Pankaj is a Biomedical Engineering student. He plans to deposit $600 that he earned as stipend, in
a bank account at 3% rate of interest compounded weekly for no more than 2 years. The total
amount of the money, A, that Pankaj will get back, is a function of time, t. Which is a reasonable
domain of the money that he may accumulate?

Answers
The correct answer is A: 600 <= money <= 2822.4.
This represents the range of possible values that Pankaj's accumulated money could fall into, given the specified conditions of the 3% interest rate compounded weekly for a maximum of 2 years. The lower bound, 600, represents the initial deposit amount, while the upper bound, 2822.4, represents the maximum amount of money Pankaj could earn after 2 years, assuming that interest is compounded every week.
Select the correct answer,
Which function defines (f + g)(x)?
(3.8)242
(2.6)241
g(x)
(f 4 g)(x) = (2.6) 2+1
(f + g)(z) = (1.8)
(f 4 g)(x)
D. (f 4 g)(z) = (28)***
A.
B.
C.
(1.8)2247242

Answers
A: (f ÷ g)(x) = (3.6)⁻²ˣ⁺¹ is the solution of the function.
What is a function?Functions are relationships that exist between a set of inputs and outputs. A function is an association of inputs, where each input is directly linked to one or more outputs. Range, codomain, and domain are all attributes of each function.
The given functions are:
f(x) = (3.6)ˣ⁺²
And g(x) = (3.6)³ˣ⁺¹
To find (f ÷ g)(x):
We take division of f(x) by g(x).
(f ÷ g)(x) = f(x) ÷ g(x)
(f ÷ g)(x) = (3.6)ˣ⁺² ÷ (3.6)³ˣ⁺¹
(f ÷ g)(x) = (3.6)ˣ⁺² ÷ (3.6)³ˣ⁺¹
(f ÷ g)(x) = (3.6)ˣ⁺² / (3.6)³ˣ⁺¹
Simplifying,
(f ÷ g)(x) = (3.6)ˣ (3.6)² / (3.6)³ˣ (3.6)¹
(f ÷ g)(x) = (3.6)ˣ⁻³ˣ (3.6)
(f ÷ g)(x) = (3.6)⁻²ˣ (3.6)
(f ÷ g)(x) = (3.6)⁻²ˣ⁺¹
Therefore, the answer is A: (f ÷ g)(x) = (3.6)⁻²ˣ⁺¹
To learn more about the function;
brainly.com/question/28303908
#SPJ1
LOTS OF POINTS Can someone provide the correct answer, and tell me what I did wrong here?

Answers
The height of the given triangle will be 13.416 cm.
Given a right-angle triangle that has a hypotenuse of 14 cm, height of x, and base of 4 cm.
The Pythagorean theorem is a fundamental principle in geometry that establishes a relationship between the sides of a right triangle. It states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
Applying the Pythagorean theorem, we can write:
\(14^2 = 4^2 + x^2\)
Simplifying the equation:
\(196 = 16 + x^2\)
Subtracting 16 from both sides:
\(180 = x^2\)
Taking the square root of both sides:
x = √180 = 6√5
Simplifying the square root:
x ≈ 13.416 cm
Therefore, the height (x) of the right-angle triangle is approximately 13.416 cm.
Learn more about right-angle triangles here:
https://brainly.com/question/3770177
#SPJ1
There was a total of 184 teachers and students at an archery lesson.
3/4
of the teachers is equal to of the students.
2/5
How many teachers were there at the archery lesson?
Answers
convert the rectangular equation to polar form.Assume a > 0x=18

Answers
To convert a rectangular equation to polar forma, we use
\(x=r\cos (\theta),y=r\sin (\theta)\)In the equation x=18, we only have x, so
\(\begin{gathered} 18=r\cos (\theta) \\ r=\frac{18}{\cos(\theta)}=18\sec (\theta) \end{gathered}\)I just need the answer pleaseI am trying to find the line of symmetry for the parabola for x

Answers
Ok, so in order to find the line of symmetry, let's compare the parabola with have with the theory.
When we have a general parabola
\(\begin{gathered} y=a{{(x-h)}^2}-k \\ y=-2(x-3)^{2}-(+4) \end{gathered}\)The theory states that the symmetry lies on x = k
So, the line of symmetry is x=4
A marching band performs on the football field at half-time. As they perform, the members of the band stand in
the shape of a sinusoidal function. While playing, they move, but still maintain the sinusoidal function,
transforming it in different ways.
Darla is a member of the marching band. As the band begins to play she is positioned in the exact center of the
field. The person closest to her on the same horizontal line, stands 10 yards away. The sinusoidal function
extends to the ends of the playing field.
The playing area of football field measure 300 feet by 160 feet. Place the playing area of a football field on the
coordinate plane such that the origin is the lower left comer of the football field.
(Score for Question 1: of 2 points)
1. What is the period and the amplitude of the sine function representing the position of the band members as
they begin to play?
Answer.
Answers
The period of the sine function representing the position of the band members is 60 feet, and the amplitude is approximately \(170.3 feet.\)
What is the coordinate plane?Since the band members are standing in the shape of a sinusoidal function, we can assume that their positions can be represented by the equation:
\(y = A sin(Bx)\)
where y is the vertical position of a band member, x is the horizontal position on the field, A is the amplitude, and B is the period.
Since Darla is positioned in the exact center of the field, and the person closest to her on the same horizontal line stands 10 yards away, we can assume that the sinusoidal function has a phase shift of 0. This means that the midline of the function passes through the point (0, 0).
To find the amplitude, we need to determine the maximum and minimum heights of the function.
Since the playing area of the football field measures 300 feet by 160 feet, the distance between the two farthest points on the field is the diagonal distance, which can be calculated using the Pythagorean theorem:
\(sqrt(300^2 + 160^2) \approx 340.6 feet\)
Since the distance between the farthest points on the field is equal to the distance between two peaks or two valleys of the sinusoidal function, the amplitude is half of this distance:
\(A = 340.6/2 \approx170.3 feet\)
To find the period, we can use the fact that the distance between two consecutive peaks or valleys is equal to the period of the function.
Since the person closest to Darla stands 10 yards away, or 30 feet away, we can assume that this person is standing at a peak or a valley of the function. This means that the period is twice the distance between Darla and the person closest to her:
\(P = 2(30) = 60 feet\)
Therefore, the period of the sine function representing the position of the band members is 60 feet, and the amplitude is approximately \(170.3 feet.\)
Learn more about coordinate here:
https://brainly.com/question/16634867
#SPJ9
Select the correct answer. Which expression is equivalent to the given expression? (6n^-5)(3n^-3)^2
Answers
The equivalenet expression is 54\(n^{-11}\)
What is expression?Any mathematical statement that includes numbers, variables, and an arithmetic operation between them is known as an expression or algebraic expression.
What is exponent?The way of representing huge numbers in terms of powers is known as an exponent. Exponent, then, is the number of times a number has been multiplied by itself.
To simplify the given expression, we need to apply the power of a power rule, which states that to raise a power to another power, we need to multiply the exponents.
Starting with:
(\(6n^-5\))(\(3n^-3\))²
We can simplify as follows:
(\(6n^-5\))(\(9n^-6\))
Now, we can use the product of powers rule, which states that when multiplying two powers with the same base, we add their exponents.
Therefore:
6 x 9 = 54
\(n^-5 * n^-6 = n^-11\)
So the simplified expression is:
\(54n^-11\)
Therefore, the expression \((6n^-5)(3n^-3)^2\) is equivalent to \(54n^-11.\)
To know more about exponent visit:
https://brainly.com/question/5497425
#SPJ1
The expression that is equal to (6n-5)(3n-3) option D, 54n11.
What is expression?Mathematical expressions consist of at least two numbers or variables, at least one arithmetic operation, and a statement.
We can use the distributive property of multiplication to expand the expression (6n - 5)(3n - 3) as follows:
(6n - 5)(3n - 3) = 6n(3n) - 6n(3) - 5(3n) + 5(3)
= 18n² - 18n - 15n + 15
= 18n² - 33n + 15
Therefore, the expression that is equivalent to (6n - 5)(3n - 3) is 18n² - 33n + 15, which is option D.
So, the answer is option D, 54n11.
To know more about expression visit:
https://brainly.com/question/18189573
#SPJ1
Determine the distance between the two points on the number line and explain your thinking

Answers
we have that
the point at left is about -3.75
the point at right is about 0.75
the distance is equal to
0.75-(-3.75)=0.75+3.75=4.50 units
Plz help this is due today NO LINKS OR GROSS PICTURES OR I Will REPORT And please show work

Answers
Answer: 15
Step-by-step explanation:
I need explanation for example 8.
Thankyou

Answers
There is a probability of 94/315 that the problem will be solved.
We are given that P has a chance of solving the problem of 2/7, Q has a chance of solving the problem of 4/7, and R has a chance of solving the problem of 4/9. To find the probability that the problem is solved, we need to consider all possible scenarios in which the problem can be solved.
The probability of this scenario is 2/7. If P solves the problem, then it does not matter whether Q or R solve it, the problem is already solved. Therefore, the probability of the problem being solved in this scenario is 2/7.
The probability of this scenario is 4/7. If Q solves the problem, then it does not matter whether P or R solve it, the problem is already solved. Therefore, the probability of the problem being solved in this scenario is 4/7.
The probability of this scenario is 4/9. If R solves the problem, then it does not matter whether P or Q solve it, the problem is already solved. Therefore, the probability of the problem being solved in this scenario is 4/9.
The probability of this scenario is (1-2/7) * (1-4/7) * (1-4/9) = 3/35. This is because the probability of P not solving the problem is 1-2/7, the probability of Q not solving the problem is 1-4/7, and the probability of R not solving the problem is 1-4/9. To find the probability of none of them solving the problem, we multiply these probabilities together.
To find the probability of the problem being solved, we need to add the probabilities of all the scenarios in which the problem is solved. Therefore, the probability of the problem being solved is:
2/7 + 4/7 + 4/9 = 94/315
To know more about probability here
https://brainly.com/question/11234923
#SPJ1
I can identify and use inverses to solve equations with one variable.

Answers
Answer:
\( \boxed{x = 4.0497}\)
Step-by-step explanation:
\( \boxed{question \: \underline{4}.} \\ 5 {x}^{2} - 7(9.5 + 3) = - 5.5 \\ 5 {x}^{2} - 66.5 - 21 = - 5.5 \\ 5 {x}^{2} = - 5.5 + 87.5 \\ 5 {x}^{2} = 82 \\ {x}^{2} = \frac{82}{5} \\ {x}^{2} = 16.4 \\ x = \sqrt{16.4} \\ \boxed{ x = 4.0496913463}\)
♨Rage♨........if you still need my help with the rest....then post each question seperatly.♨
PLEASE PLEASEE ANSWER THE QUESTION IN THE PICTURE BELOW
which form most quickly reveals the vertex?
And what is the vertex??

Answers
Answer: Choice C
Vertex = (5, -2)
===============================================
Explanation:
Vertex form is \(y = a(x-h)^2 + k\) where the vertex itself is located at (h,k)
As the name implies, we can very quickly pull out the coordinates of the vertex without doing much math at all.
In the case of choice C, we have \(y= \frac{1}{2}(x-5)^2 - 2\) which is the same as \(y = \frac{1}{2}(x-5)^2 + (-2)\) and we can see that h = 5 and k = -2. Therefore, the vertex is located at (h,k) = (5, -2)
Suppose two initial vectors intersect at a right angle and form a resultant vector. The magnitudes of one initial vector, A, and the resultant vector, R, are given.
Which formula can be used to find the magnitude of the other initial vector, B?
Answers
Answer:
Step-by-step explanation:
B = √(R² - A²)
Which of the following are solutions to the equation cos^2 2x-1/4=0? Check all that apply.
A. 11pi/3
B. 12pi/6
C. 5pi/6
D. Pi/6
Answers
Answer:
D
Step-by-step explanation:
Cos^2 2x=1/4
Cos 2x =+-1/2
2x=z
Cos z=+-1/2
z1=pi/3
z2=11pi/3
z1 and z2 are possible.
x1=pi/6
x2=11pi/6
Find the equation of the line shown below

Answers
Answer:
y = -3/2x-6
Step-by-step explanation:
y-intercept = - 6
Slope = - 3/2
please answer !!Urgent

Answers
I'm sorry I don't know what this is can you explain it sike