A balloon is being filled with helium at the rate if 4 ft^3/min. What is the rate, in ft2/min, at which the surface area is increasing when the volume is 32π/3 ft^3?The answer is = 4ft^2/min
Answers
The correct answer is the rate at which surface area of spherical balloon is increasing is 4ft²/min.
It is given that volume of balloon = 32\(\pi\)/3 ft³
and a balloon is being filled with helium at the rate if 4 ft³/min
thus, dv/dt = 4
⇒ (4/3)\(\pi\)r³ =32\(\pi\)/3
⇒ 4r³ = 32
⇒ r³ = 8
⇒ r =2
Radius of balloon= 2ft
∵ v =( 4/3)\(\pi\) r³
⇒ dv/dt = \(\frac{4}{3}\)\(\pi\).3r² \(\frac{dr}{dt}\)
⇒ 4 = 4\(\pi\) r² dr/dt
⇒ 4 = 4 \(\pi\)(4) dr/dt
∴dr/dt = 1/4\(\pi\)
Let the surface area of balloon be A.
surface area = A = 4 \(\pi\)r²
Differentiating A with respect to t
⇒ dA/dt = 4\(\pi\) (2r)dr/dt
= 8\(\pi\) ×(2×2) ×1/4\(\pi\) (∵ r=2 , dr/dt = 1/4\(\pi\))
= 4 sq.ft /min
Hence, the rate at which surface area is increasing is 4ft²/min.
To know more about 'surface area' related questions
visit- https://brainly.com/question/14282016
#SPJ4
Related Questions
help quickly please!! in the cafeteria, tables are arranged in groups of 4, with each table seating 6 students how many students can sit at 8 groups of tables? write the rule you used to find the number of students.
Answers
Answer:
The answer is 320.
the rule i used was y=32x and x represents the # of groups of tables.
Consider a large-sample level 0.01 test for testing H_0: p = 0.2 against H_a: p > 0.2. For the alternative value p = 0.21, compute beta(0.21) for sample sizes n = 81, 900, 14, 400, 40, 000, and 90, 000. (Round your answers to four decimal places.) For p^= x/n = 0.21, compute the P-value when n = 81, 900, 14, 400, and 40, 000. (Round your answers to four decimal places.)Previous question
Answers
These are the computed values of beta and p-value for the given alternative value p = 0.21 and sample sizes.
To compute the beta (β) for the given alternative value p = 0.21 and sample sizes n = 81, 900, 14,400, 40,000, and 90,000, we need to determine the probability of Type II error. Beta is the probability of failing to reject the null hypothesis (H₀) when the alternative hypothesis (Hₐ) is true.
To calculate beta, we need to find the corresponding z-value for the given significance level α = 0.01, which corresponds to a z-value of 2.33 (approximate value).
Using the formula for the standard deviation of the sample proportion:
σ = sqrt((p₀ * (1 - p₀)) / n)
where p₀ is the null hypothesis value, p = 0.2, and n is the sample size.
Then we can calculate the z-score for the alternative value p = 0.21 using the formula:
z = (p - p₀) / σ
Finally, we can compute beta using the standard normal distribution table or a statistical calculator.
Let's calculate beta for the given sample sizes:
For n = 81:
σ = sqrt((0.2 * (1 - 0.2)) / 81) ≈ 0.0447
z = (0.21 - 0.2) / 0.0447 ≈ 0.2494
beta = P(Z > 0.2494) ≈ 0.4013
For n = 900:
σ = sqrt((0.2 * (1 - 0.2)) / 900) ≈ 0.0143
z = (0.21 - 0.2) / 0.0143 ≈ 0.7692
beta = P(Z > 0.7692) ≈ 0.2206
For n = 14,400:
σ = sqrt((0.2 * (1 - 0.2)) / 14,400) ≈ 0.0071
z = (0.21 - 0.2) / 0.0071 ≈ 1.5493
beta = P(Z > 1.5493) ≈ 0.0606
For n = 40,000:
σ = sqrt((0.2 * (1 - 0.2)) / 40,000) ≈ 0.0050
z = (0.21 - 0.2) / 0.0050 ≈ 2.2000
beta = P(Z > 2.2000) ≈ 0.0139
For n = 90,000:
σ = sqrt((0.2 * (1 - 0.2)) / 90,000) ≈ 0.0033
z = (0.21 - 0.2) / 0.0033 ≈ 3.0303
beta = P(Z > 3.0303) ≈ 0.0012
Next, let's calculate the p-value for the alternative value P = 0.21 and sample sizes n = 81, 900, 14,400, and 40,000.
The z-score for the given P can be calculated using the formula:
z = (P - p₀) / σ
Using the standard normal distribution table or a statistical calculator, we can find the area under the curve beyond the calculated z-score to obtain the p-value.
For n = 81:
σ = sqrt((0.2 * (1 - 0.2)) / 81) ≈ 0.0447
z = (0.21 - 0.2) / 0.0447 ≈ 0.2494
p-value = P(Z > 0.2494) ≈ 0.4013
For n = 900:
σ = sqrt((0.2 * (1 - 0.2)) / 900) ≈ 0.0143
z = (0.21 - 0.2) / 0.0143 ≈ 0.7692
p-value = P(Z > 0.7692) ≈ 0.2206
For n = 14,400:
σ = sqrt((0.2 * (1 - 0.2)) / 14,400) ≈ 0.0071
z = (0.21 - 0.2) / 0.0071 ≈ 1.5493
p-value = P(Z > 1.5493) ≈ 0.0606
For n = 40,000:
σ = sqrt((0.2 * (1 - 0.2)) / 40,000) ≈ 0.0050
z = (0.21 - 0.2) / 0.0050 ≈ 2.2000
p-value = P(Z > 2.2000) ≈ 0.0139
To know more about p-value,
https://brainly.com/question/15839377
#SPJ11
The difference between the park and house of a student is 1Km 575m. Every day he walks both ways between the park and his house. Find the total distance covered by him in a week's time?
Answers
The student covers a total distance of 22.05 kilometers in a week's time, walking between the park and the house each day.
To find the total distance covered by the student in a week's time, we need to calculate the distance covered in one round trip (from the house to the park and back) and then multiply it by the number of round trips in a week.
Given that the difference between the park and house is 1 kilometer and 575 meters, we can convert it to a total distance of 1.575 kilometers.
In a round trip, the student covers twice the distance between the park and the house, which is 1.575 kilometers * 2 = 3.15 kilometers.
Now, we need to determine how many round trips the student makes in a week. Let's assume the student makes one round trip each day.
Since there are 7 days in a week, the total distance covered by the student in a week's time is 3.15 kilometers * 7 = 22.05 kilometers.
for similar questions on distance.
https://brainly.com/question/26046491
#SPJ8
A straight angle equals 180 degrees is true or false?
Answers
Answer:
True
Step-by-step explanation:
Straight angles are straight lines which equal 180 degrees
Answer:
true it is equals 180 for that angle
Given mlln, find the value of X.

Answers
Answer:
65°
Step-by-step explanation:
180-115=65
Have a great day
Answer:
\(\displaystyle\Huge \bf\red{\underline{\underline{ANSWER}}}
\)
Let the speed of the train be x km/hr and the speed of the bus is y km/hr.
So according to question and using
\( \huge \boxed{\sf{Time = \frac{Distance}{speed}}}
\)
Total distance =300 km
Mansi travels 60 km by train and 300−60=240 by bus in 4 minute,
\( \bf\frac{60}{x} + \frac{240}{y} = \red4
\)
and 100 km by train, 300−100=200 by bus, and takes 10 minutes more,
\( \bf {\frac{100}{x} + \frac{200}{y} = 4 + \frac{1}{6} = \frac{24 + 1 }{6} = \purple{\frac{25}{6}}}
\)
Now, let
\(\bf\color{blue}{\frac{1}{x} = a}\)
and.
\( \bf \color{blue}{ \frac{1}{y} = b }\)
\(\bfthen 60a+240b=4.............(1)\)
\(\bf100a+200b=25/6----(2)\)
multiply (1) by 5 and (2) by 6 we get
\(\bf300a+1200b=20..........(3)\)
\(\bf600a+1200b=25...........(4)\)
Subtracting (3) and (4) we get
\(\bf \green{−300a=−5}\)
\(\bf{a = \frac{1}{60}}\)
Putting the value of a in (1) we get
\(\bf{60 \times \frac{1}{60} + 240b = 4}\)
\(
\bf240b = 3 \\ \\ \bf b = \frac{1}{80} \)
Now ,
\( \bf\frac{1}{x} = a \\ \\ \bf \red{a = 60 km/h \: \blue \bigstar}\)
\( \bf\frac{1}{y} = b \\ \\ \bf \red {b = 80 km/h \: \pink \bigstar} \)
Hence, the speed of the train is 60 km/hr and the speed of the bus is 80 km/hr.
Can someone help me please


Answers
Answer: it should be x
Step by step explanation: the x table changes at a rate of 6 when the y table changes at a rate of 4
Drag each division expression to the correct location on the table.
Solve each division problem, and classify it based on its quotient.

Answers
There are three expressions having quotient 6 are:
4 2/3 ÷ 7/9
9 ÷ 3/2
12/7 ÷ 2/7
There are three expressions having quotient 9 are:
4 1/2 ÷ 1/2
21 ÷ 7/3
72/7 ÷ 8/7
What is division?The splitting of a large group into smaller groups such that every group will have an equal number of items.
We have,
Finding quotient for each expression.
1.
4 2/3 ÷ 7/9
= 14/3 ÷ 7/9
= 14/3 x 9/7
=6
2.
9 ÷ 3/2
= 9 x 2/3
= 6
3.
4 1/2 ÷ 1/2
= 9/2 x 2/1
= 9
4.
21 ÷ 7/3
= 21 x 3/7
= 9
5.
12/7 ÷ 2/7
= 12/7 x 7/2
= 6
6.
72/7 ÷ 8/7
= 72/7 x 7/8
= 9
Thus,
Expression having quotient 6:
- 4 2/3 ÷ 7/9
- 9 ÷ 3/2
- 12/7 ÷ 2/7
Expression having quotient 9:
- 4 1/2 ÷ 1/2
- 21 ÷ 7/3
- 72/7 ÷ 8/7
Learn more about division here:
https://brainly.com/question/1575906
#SPJ1
Find the coordinates of the point 7/10 of the way from A to B

Answers
Answer:
D = (9,4) - (-4, -7) = (13,11) where D is length of line between A and B
.7 D = (9.1, 7.7) since .7 * 13 = 9.1 and .7 * 11 = 7.7
Thus we merely need to add these amounts to point A
(-4, -7) + (9.1, 7.7) = (5.1, .7) for the final coordinates
Example 1 what surfaces in double-struck r3 are represented by the following equations? (a) z = 3 (b) y = 5
Answers
In double-struck ℝ³ (ℝ³), the surfaces represented by the given equations are as follows, In both cases, the surfaces are planes in ℝ³.
y = 5
z = 3
(a) The equation z = 3 represents a plane parallel to the xy-plane, located at a distance of 3 units above the origin. This plane intersects the yz-plane and xz-plane in lines parallel to the y-axis and x-axis, respectively.
(b) The equation y = 5 represents a plane parallel to the xz-plane, located at a distance of 5 units above the origin. This plane intersects the xy-plane and yz-plane in lines parallel to the x-axis and z-axis, respectively.
Learn more about Planes here:
https://brainly.com/question/18681619
#SPJ11
In the three-dimensional Euclidean space, ℝ³, the surfaces represented by the equations z = 3 and y = 5 correspond to a horizontal plane parallel to the xy-plane at a height of 3 units above the origin and a vertical plane parallel to the xz-plane intersection the y-axis at a value of 5, respectively.
(a) The equation z = 3 represents a surface that is a horizontal plane parallel to the xy-plane. This means that for any point (x, y, z) on this surface, the z-coordinate is always equal to 3. It forms a flat plane at a height of 3 units above the origin (0, 0, 0). This plane is perpendicular to the z-axis and extends infinitely in the x and y directions.
(b) The equation y = 5 represents a surface that is a vertical plane parallel to the xz-plane. For any point (x, y, z) on this surface, the y-coordinate is always equal to 5. This plane intersects the y-axis at a value of 5 and extends infinitely in the x and z directions. It is perpendicular to the y-axis.
In both cases, the equations define surfaces that are infinite in extent and have specific geometric orientations relative to the coordinate axes in ℝ³.
Know more about Intersection here: https://brainly.com/question/33609758
#SPJ11
A group of statements that executes as a single unit is a(n) ____.
a. module
b. unit
c. bunch
d. block
Answers
The term that describes a group of statements that executes as a single unit is a "block". A block of code is a program that is grouped together and treated as a single unit. So, the correct option is D.
In computer programming, a block is a group of statements or declarations that are enclosed within a set of curly braces ({ }). The block serves as a single unit that is executed together. Blocks are used to organize code and to apply control structures, such as loops and conditional statements, to multiple statements.
A block can contain any number of statements, which can include variable declarations, function calls, loops, conditional statements, and other constructs. The statements within a block are executed in sequence, one after another, unless a control statement is encountered that alters the normal sequence of execution.
For example, a while loop in Java consists of a block of code that is executed repeatedly while a certain condition is true:
while (condition) {
// block of code to be executed while condition is true
}
In this example, the block of code inside the curly braces will be executed repeatedly while the condition specified in the while statement is true. The block can contain any number of statements, and these statements will be executed each time the loop iterates.
Another common use of blocks is to define functions or methods. A function or method is a block of code that can be called from other parts of the program, and can take inputs (arguments) and return outputs. For example, in Python, a function can be defined as follows:
def function(argument1, argument2):
# block of code to be executed in the function
return result
In this example, the block of code enclosed within the function definition is executed when the function is called. The function can take inputs (argument1 and argument2), which can be used within the function, and it can return a result using the return statement.
To learn more about statements click on,
https://brainly.com/question/29891964
#SPJ4
Describe the long run behavior of f(x)=5(2)x+1:
As x→−[infinity], f(x) =
As x→[infinity], f(x) =
Answers
The long run behavior of the function f(x)=5(2)x+1 is that it approaches 1 as x approaches negative infinity and it approaches infinity as x approaches positive infinity.
The long-term behavior of the function f(x)=5(2)x+1 can be discovered by examining how the function behaves as x gets closer to negative and positive infinity.
As x→−[infinity], f(x) = 5(2)^ -∞+1 = 5(0)+1 = 1
As x approaches negative infinity, the value of the function approaches 1.
As x→[infinity], f(x) = 5(2)^ ∞+1 = 5(∞)+1 = ∞
As x approaches positive infinity, the value of the function approaches infinity.
As a result, the function f(x)=5(2)x+1 behaves in the long run in such a way that it approaches 1 as x approaches negative infinity and infinity as x approaches positive infinity.
Learn more about behavior at https://brainly.com/question/22443880
#SPJ11
How can I find X ın thıs equatıon? I've tried dividing this in reverse and it still didn't work.

Answers
Answer:
x=4
Step-by-step explanation:
Well bud, you may have overthought this one a bit too much. It pretty much requires one simple move and then you good. All you gott do is multiply both sides by (-6/5) and that in itself isolates x. This was done because inverses cancel out to 1, and a negative 1 times a negative 1 equals a positive 1. What you get after multiplying both sides by (-6/5) is x=(-10/3)(-6/5) Now all you have to do is multiply and simplify, giving you x=4. You should be gucci now, cuz I got you homie. ;)
Will mark brainiest

Answers
ur welcome
Gil is shopping for books and CDs. He buys 4 books and no CDs for a total of $32. Write an equation that represents the relationship between the cost of a book, y, and the cost of a CD, x, in standard form.
Answers
Gil is out purchasing CDs and books. He spends $32 on 4 books but not any CDs. A standard form equation y=-8n and x=0.
Given that,
Gil is out purchasing CDs and books. He spends $32 on 4 books but not any CDs.
We have to create a standard form equation to show the connection between the price of a book (y) and the price of a CD (x).
The equations in standard form for Gil's change in money after purchasing a book (y) and his change in money after selling a CD (x).
Gil spends $32 on 4 books.
4 books = $32
1 book = $8
If n is the total number of books bought, the change in currency equals
y=-8n.
Here, the negative sign stands for a decline in currency. Here, a slope of -8 indicates that after purchasing each book, the money declined by $8.
There are no CDs so x=0.
Therefore, y=-8n and x=0.
To learn more about books visit: https://brainly.com/question/17061364
#SPJ1
Select three side lengths, in centimeters (cm), that can form a right triangle. Use the Pythagorean Theorem.
A. 5cm
B. 6cm
C. 8cm
D. 10cm
E. 11cm
F.12cm
Answers
The side lengths 8 cm, 6 cm, and 10 cm that can form a right triangle option (B), (C), and (D) are correct.
What is a right-angle triangle?It is defined as a triangle in which one angle is 90 degrees and the other two angles are acute angles. In a right-angled triangle, the name of the sides are hypotenuse, perpendicular, and base.
We know that Pythagoras theorem:
\(\rm Hypotenuse^2 = Perpendicular^2 + Base^2\)
10² = 8² + 6² = 64+36 = 100
Thus, the side lengths 8 cm, 6 cm, and 10 cm that can form a right triangle option (B), (C), and (D) are correct.
Learn more about the right angle triangle here:
brainly.com/question/3770177
#SPJ2
Which value(s) is a solution for the inequality f < 4? Choose all that apply.

Answers
f = -4
f = 3
f = -2
Explanations:f < 4 means that f consists of all the values that are less than 4.
From the options:
Numbers that are less than 4 are -4, 3 and -2.
7 is greater than 4, therefore, f = 7 is an incorrect choice
The sum of 110 and a number
is five times that number
minus 10. What is the
number?
Answers
Answer: Let the number = x
5x+10 = 120
Or, 5x = 120 - 10
Or, 5x = 110
Or, x = 110/5
Or, x = 2
Step-by-step explanation:
for what values of p is the series ∑n=1[infinity](−1)nnnp 2 conditionally convergent?
Answers
The values of p for which the series ∑(n=1)^(∞) ((-1)^n / (n^p)) converges conditionally are p > 0.
To determine the values of p for which the series ∑(n=1)^(∞) ((-1)^n / (n^p)) converges conditionally, we can apply the alternating series test.
According to the alternating series test, a series of the form ∑((-1)^n * b_n) converges conditionally if:
1. The terms b_n are positive and decreasing (|b_n+1| ≤ |b_n|), and
2. The limit of b_n as n approaches infinity is 0 (lim(n→∞) b_n = 0).
In this case, our terms are b_n = 1 / (n^p). Let's check these conditions:
1. The terms are positive and decreasing:
To satisfy this condition, we need to show that |(1 / ((n+1)^p))| ≤ |(1 / (n^p))| for all n.
Taking the ratio of consecutive terms:
|(1 / ((n+1)^p)) / (1 / (n^p))| = (n^p) / ((n+1)^p) = (n / (n+1))^p.
Since (n / (n+1)) is less than 1 for all n, raising it to the power p will still be less than 1 for p > 0. Therefore, the terms are positive and decreasing.
2. The limit of the terms as n approaches infinity is 0:
lim(n→∞) (1 / (n^p)) = 0 for p > 0.
Based on the conditions of the alternating series test, the series converges conditionally for p > 0.
Therefore, the values of p for which the series ∑(n=1)^(∞) ((-1)^n / (n^p)) converges conditionally are p > 0.
To know more about conditionally convergent refer here:
https://brainly.com/question/31064900#
#SPJ11
Which of the following is an example of a statistical question?
Question 1 options:
How many cars did Toyota make last year?
How many people wear size 8 shoes in this class?
How many dogs do each of you have?
How many students have dogs in this school?
Answers
The other questions could all be one answer, like, “there are two people that wear size eight shoes” or “29 students have dogs in this school” or “Toyota made 90 cars last year”
But the third option, one person could have one dog, another could have four, another could have none. The answers will vary and there will be multiple
If this answer helped you, I would appreciate a brainliest!
Suppose we have some algorithm which process arrays of n elements. It takes n
2
steps to process the first element, but it only takes 2n steps each to process the remaining elements. Using any of the amortized analysis techniques from the slides, find the amortized runtime per element for the algorithm to complete. Show your work, and express your answer in Big O notation.
Answers
The given algorithm can be found using the aggregate analysis technique. In this case, we calculate the total number of steps required to process all n elements and then divide it by n to obtain the amortized runtime per element.
The algorithm takes n^2 steps to process the first element, and for the remaining (n-1) elements, it takes 2n steps each. Therefore, the total number of steps required can be calculated as follows:
n^2 + (n-1) * 2n = n^2 + 2n^2 - 2n = 3n^2 - 2n.
Dividing this by n, we get the amortized runtime per element: (3n^2 - 2n) / n = 3n - 2.
Expressing the amortized runtime in Big O notation, we drop the constant term and lower-order terms, resulting in O(n).
The amortized runtime per element for the given algorithm is O(n), meaning that on average, each element takes linear time to process. This analysis accounts for the initial costly processing of the first element and the subsequent efficient processing of the remaining elements.
Learn more about algorithm here:
brainly.com/question/31936515
#SPJ11
Copy ofJIM 821 Projecting and sudi
carla Shumake
1.3: Scaled Rectangles 1
Here is a picture of Rectangle R, which has been
evenly divided into smaller rectangles. Two of the
smaller rectangles are labeled B and C.
Is B a scaled copy of R? If so, what is the scale factor?
Rectangle R
Yes
No
B
US
06:35
Answers
Solve the equation please!!!!!

Answers
Answer:
x = 4 ; y = 12
Step-by-step explanation:
y = 3x
5x - 3x = 8
2x = 8
2/2 x = 8/2
x = 4
y = 3(4)
y = 12
y = 3 x 4

YALL BETTER ANSWER THIS PLSSSSSSSSSSS

Answers
Answer:
= 3/16(0.1875)Step-by-step explanation:
explanation in the image.
Answer:
Step-by-step explanation:
Take out lignes
-1/4x-3/7
= -7/12
exercise 1.12. we roll a fair die repeatedly until we see the number four appear and then we stop. (a) what is the probability that we need at most 3 rolls?
Answers
The probability that we need at most 3 rolls to see the number four appear is 7/8.
we can analyze the possible outcomes. In the first roll, there are 6 equally likely outcomes since each face of the die has an equal chance of appearing. Out of these 6 outcomes, only one outcome results in seeing the number four, while the other 5 outcomes require additional rolls. Therefore, the probability of needing exactly one roll is 1/6.
In the second roll, there are two possibilities: either we see the number four (with a probability of 1/6) or we don't (with a probability of 5/6). If we don't see the number four in the second roll, we proceed to the third roll.
In the third roll, the only remaining possibility is seeing the number four, as we must stop rolling after this point. The probability of seeing the number four in the third roll is 1/6.
To find the probability of needing at most 3 rolls, we sum up the probabilities of these three independent events: 1/6 + (5/6)(1/6) + (5/6)(5/6)(1/6) = 7/8. Hence, the probability that we need at most 3 rolls is 7/8.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
does a piecewise function always have an x and y intercept
Answers
Answer:yes
Step-by-step explanation:
but if the y intercept is 0 then it’ll show like: y= 3x which is equal to y=3x plus or minus 0
No, a piecewise function does not always have an x and y intercept.
A piecewise function is a function that is defined by multiple sub-functions, each of which applies to a certain interval of the main function's domain.
An x-intercept is the point where the function crosses the x-axis, and a y-intercept is the point where the function crosses the y-axis.
It is possible for a piecewise function to not have an x or y intercept if none of the sub-functions cross the x or y axis. For example, the piecewise function f(x) = {2x + 1 for x < 0, -2x + 1 for x > 0} does not have an x or y intercept because neither of the sub-functions cross the x or y axis.
In conclusion, a piecewise function does not always have an x and y intercept. It depends on the sub-functions that make up the piecewise function.
Learn more about Piecewise Function here: brainly.com/question/12561612
#SPJ11
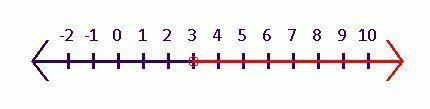
Graph the solution to this inequality on the number line.
0.3(x − 4) > -0.3
Answers
Answer:
Please refer to the attached image in the answer area.
Step-by-step explanation:
The given inequality is:
\(0.3(x -4) > -0.3\)
To find:
The graph of inequality on the number line.
Solution:
First of all, let us simplify the inequality.
\(0.3(x -4) > -0.3\)
Dividing it with 0.3 on the both sides:
\(x -4 > -1\\\text{Adding 4 on both sides}\\\Rightarrow x > 3\)
i.e. all the values x > 3 will be our solution. There is no equal sign in the inequality so 3 will not be included in the solution.
Please refer to the attached image for the solution graph of the given inequality.
3 has an empty circle drawn over it which signifies that 3 is not included in the solution set.
Red line shows that all the values greater than 3 are included in the solution.
Find 172% of 850. (pls help)
Answers
Answer:
172/100x850
Step-by-step explanation:
1462
dave plays basketball 3 out of the 5 weekdays. how many possible schedules are there to play basketball on wednesday or monday or both?
Answers
There are 9 possible schedules to play basketball such that dave can play on monday or wednesday or both which is union of two set .
so this question seems like we have to take union of ways of palying on monday or wednesday
let n(m) be number of ways of playing on monday
n(w) be number of ways of playing on wednesday
we have to find n(m∪w)
n(mUw) = n(m) +n (w) - n(m∩ w)
so n(m) = \(4_C__2\) as one day is now fixed which is monday so we have 4 available days and 2 days to play.
n(m) = \(4_C__2\) = 6
similary n(m) = n(w) = 6
now n(m∩w) = \(3_C__1\) as now we have 2 fixed day and we have 3 day remaining and only one day to play.
n(m∩w) = \(3_C__1\) =3
now n(mUw) = n(m) +n (w) - n(m∩ w)
=> 6 + 6 -3
=> 12 - 3
so n(mUw) = 9
so we have 9 schedules to paly keeping condition given in the question.
To know more about union of set click on link below:
https://brainly.com/question/29055360#
#SPJ4
find a particular solution to the nonhomogeneous differential equation y′′ 4y′ 5y=15x 3e−x.
Answers
The particular solution yp(x) is: yp(x) = 3x - 12/5 + 3e⁽⁻ˣ⁾
How to determine particular solution to the nonhomogeneous differential equationTo find a particular solution to the nonhomogeneous differential equation y'' + 4y' + 5y = 15x + 3e⁽⁻ˣ⁾, we will use the method of undetermined coefficients.
First, we need to make a guess for the form of the particular solution. Let's denote yp as the particular solution.
Since the right-hand side of the equation is a linear function plus an exponential function, we will guess the following form for yp:
yp(x) = Ax + B + Ce⁽⁻ˣ⁾
Now, we need to differentiate yp(x) to obtain its first and second derivatives:
y'p(x) = A - Ce⁽⁻ˣ⁾
y''p(x) = C × e⁽⁻ˣ⁾
Substitute yp(x), y'p(x), and y''p(x) into the given differential equation:
C × e⁽⁻ˣ⁾+ 4(A - Ce⁽⁻ˣ⁾) + 5(Ax + B + Ce⁽⁻ˣ⁾) = 15x + 3e⁽⁻ˣ⁾
Now, we need to match the coefficients on both sides:
For e⁽⁻ˣ⁾ terms: C + 4(-C) + 5(C) = 3 C = 3 For x terms:
5A = 15 A = 3
For constant terms: 4A + 5B = 0 12 + 5B = 0 B = -12/5
So, the particular solution yp(x) is:
yp(x) = 3x - 12/5 + 3e⁽⁻ˣ⁾
Learn more about non homogeneous equation at
https://brainly.com/question/14349870
#SPJ11
8. Alice Corporations has two divisions. The one in the high-risk industry has a beta of 1.5 and can be financed optimally in line with others in the industry at 25% debt and 75% equity. The low risk division has a beta of .8 and based on industry averages, can be financed optimally at 50% debt and 50% equity. Assuming the risk-free rate of return on 10-year government securities is 2.7% and the market risk premium is 5%. What is the estimated cost of common equity for the high-risk division
Answers
The estimated cost of common equity for the high-risk division of Alice Corporations can be calculated using the Capital Asset Pricing Model (CAPM). Hence, the estimated cost of common equity for the high-risk division is 10.2%.
The Capital Asset Pricing Model (CAPM) is commonly used to estimate the cost of equity. It is based on the relationship between the expected return on an investment and its systematic risk (measured by beta). The formula for estimating the cost of equity using CAPM is as follows:
Cost of Equity = Risk-Free Rate + Beta * Market Risk Premium
Since the high-risk division can be financed optimally in line with others in the industry at 25% debt and 75% equity, we can assume that the beta for the division represents the weighted average of the industry's beta. Therefore, the estimated beta for the high-risk division is 1.5.
Plugging in the values into the CAPM formula:
Cost of Equity = 2.7% + 1.5 * 5%
= 2.7% + 7.5%
= 10.2%
Hence, the estimated cost of common equity for the high-risk division is 10.2%. This represents the expected return on equity based on the risk profile of the division as measured by its beta and the overall market conditions.
Learn more about Capital Asset Pricing Model here:
https://brainly.com/question/32230922
#SPJ11