A bag of M&M's has 6 red, 3 green, 8 blue, and 5 yellow M&M's. What is the probability of randomly picking: (give answer as a reduced fraction) 1) a yellow? 2) a blue or green? 3) an orange?
Answers
The probability of randomly picking a yellow M&M is 5/22.
There are no orange M&M's in the bag, so the probability of randomly picking an orange M&M is 0.
What is the probability of randomly picking 1) a yellow? 2) a blue or green? 3) an orange?There are 22 M&M's in the bag in total. We can use this information to answer the following:
The probability of randomly picking a yellow M&M is 5/22.
The of randomly picking a blue or green M&M is the sum of the probabilities of picking a blue M&M and a green M&M, since these events are mutually exclusive(i.e., they cannot occur at the same time). The probability of picking a blue M&M is 8/22, and the probability of picking a green M&M is 3/22. Therefore, the probability of picking a blue or green M&M is (8/22) + (3/22) = 11/22.
There are no orange M&M's in the bag, so the probability of randomly picking an orange M&M is 0.
to know more about probability
brainly.com/question/30034780
#SPJ1
Related Questions
If f(x) = 4x + 12 is graphed on a coordinate plane, what is the y-intercept of the graph?
4
8
12
16
Answers
Answer: y-intercept is 12
Step-by-step explanation:
y = mx +b
m = slope
b = y-intercept
y | = | x | + | b
f(x) | = | 4x | + | 12
b = y-intercept
2x − 6y = 12
−x + 3y = 1
For the following exercises, determine whether the lines given by the equations below are parallel, perpendicular, or neither parallel nor perpendicular:
Answers
We are given the following set of equations,
\(2x-6y=12 \\ -x+3y=1\)
and asked to determine whether they are parallel, perpendicular or neither. We first need to alter each equation and put into slope-intercept form, \(y=mx+b\) (m=slope/rate of change, b=y-intercept). Then we can follow the following basic guidelines,
\(\Rrightarrow\) Lines that are parallel will have slopes that are equal (\(m =m\)) .
\(\Rrightarrow\) Lines that are perpendicular will have slopes that are reciprocal, opposite signs (\(m \rightarrow -\frac{1}{m}\)).
\(\Rrightarrow\) Lines that are neither will have slopes that are NOT equal (\(m_{1} \neq m_{2}\)).
Taking the first equation, \(2x-6y=12\), and putting it in slope-int form.
\(\Longrightarrow2x-6y=12\)
\(\Longrightarrow-6y=12-2x\)
\(\Longrightarrow y=\frac{12}{-6} -\frac{2}{-6} x\)
\(\Longrightarrow y=-2+\frac{1}{3} x\)
\(\Longrightarrow y=\frac{1}{3} x -2\)
The slope of line 1 is \(\frac{1}{3}\).
Now taking the second equation, \(-x+3y=1\), and putting it in slope-int form.
\(\Longrightarrow -x+3y=1\)
\(\Longrightarrow 3y=1+x\)
\(\Longrightarrow y=\frac{1}{3} +\frac{x}{3}\)
\(\Longrightarrow y=\frac{1}{3}x +\frac{1}{3}\)
The slope of line 2 is \(\frac{1}{3}\).
Since the slopes of each line are equal, than the lines are parallel.
. Joaquin played basketball with his friends from 1:10 to 3:35. He arrived home 20 minutes later. How many minutes passed from the time Joaquin started playing basketball until the time he arrived at home?
Answers
Answer:
165 minutes
Step-by-step explanation:
To solve for the number of minutes that Joaquin played for, we can use this expression:
(let 'a' represent how much time passed from the time Joaquin started playing basketball until the time he arrived at home)
1:10 + a = 3:35Subtracting 1:10 from each side:
1:10 - 1:10 + a = 3:35 - 1:101:10 - 1:10 cancels out to 0, while 3:35 - 1:10 is equal to 2:25.
So, the expression is now:
a = 2:25So, 2 hours and 25 minutes passed.
If we know that 1 hour is equivalent to 60 minutes, we can use this expression to solve for however many minutes are in 2 hours:
2 × 60 = 120Now we need to add on the number of minutes and the time it took him to get home:
120 + 25 + 20 = 165Therefore, 165 minutes passed from the time Joaquin started playing basketball until the time he arrived at home.
What is (5b + 3x)(5d-3b)
Answers
someone please help me giving brainlist

Answers
Answer:
A
Step-by-step explanation:
A cell phone towerbcast a shadow that is 40 feet long . An 10- foot- tall stop sign located near the tower casts a shadow that is 8 feet long. How tall is the cell phone tower?
Answers
Using proportions, considering the relation between the height and the shadow, it is found that the cell phone tower is 50 feet.
What is a proportion?A proportion is a fraction of a total amount, and the measures are related using a rule of three.
When the shadow is of 8 feet, the height is of 10 feet. What is the height when the shadow is of 40 feet? The rule of three is:
8 feet - 10 feet
40 feet - h feet
Applying cross multiplication:
8h = 10 x 40
Simplifying by 8:
h = 10 x 5 = 50 feet.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
Angel buys a $30,100 sports car and has a monthly payment of $584.92 over 5 years with an annual APR of 6.2%. Part A: [Must show equation] Determine the total amount paid to the bank over the course of the loans. Part B: Then determine the total finance charge paid to the bank
Answers
Answer:
A. $35,095.2
B. $4,995.2
Explanation:
The total amount paid to the bank can be calculated as the monthly payment multiplied by the number of months in the course of the loan. So, it is equal to:
Total = $584.92 x 5 years x 12 months
Total = $35,095.2
On the other hand, the total finance charge paid to the bank can be calculated as the total amount paid to the bank less the initial cost of the car, so:
$35,095.2 - $30,100 = $4,995.2
Therefore, the answers are:
A. $35,095.2
B. $4,995.2
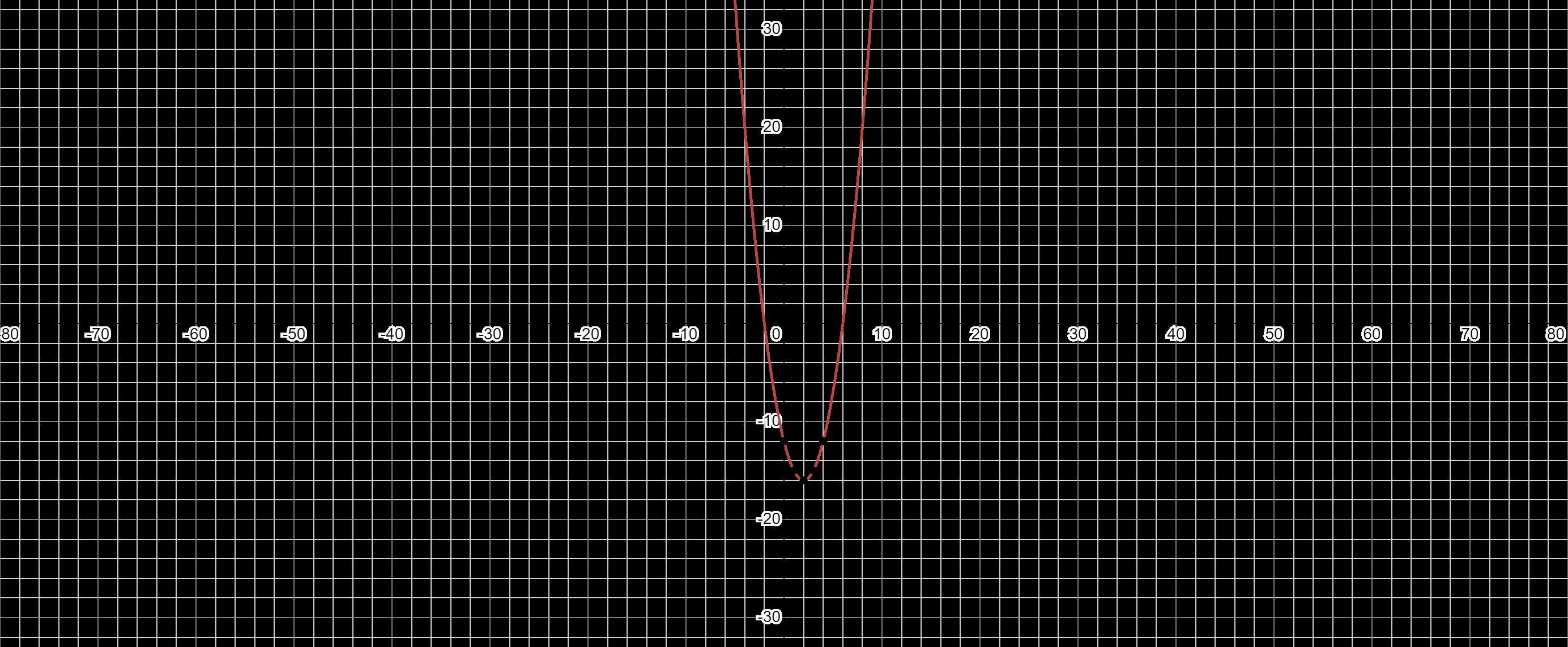
find n. (n!)²- 4n! - 12 = 0
Answers
Answer:
n=6 , n=-2
Step-by-step explanation:
\(n^{2}-4n-12=0\)
Factorise to give:
\((n-6)(n+2)\)
Set first one to equal 0:
\(n-6=0\)
\(n=6\)
Set second one to equal 0:
\(n+2=0\)
\(n=-2\)
Reason for 2 solutions:
All quadratics can have a maximum of 2 solutions like this one or a minimum of 0.
The solution(s) is the point where the graph crosses the x-axis
The image below shows the graph of the equation:
\(n^{2}-4n-12\)
When y=0:
It intercepts the x-axis at 6 and -2 giving why n has 2 solutions
What is the additive inverse of the complex number 9-4i?
Answers
Answer:
\( \frac{1}{9 - 4i} \)
I'm not sure
\(\lim_{n \to \0}(x/(tan(x))^(cot(x)^2 )\)
Answers
It looks like the limit you want to compute is
\(\displaystyle L = \lim_{x\to0}\left(\frac x{\tan(x)}\right)^{\cot^2(x)}\)
Rewrite the limand with an exponential and logarithm:
\(\left(\dfrac{x}{\tan(x)}\right)^{\cot^2(x)} = \exp\left(\cot^2(x) \ln\left(\dfrac{x}{\tan(x)}\right)\right) = \exp\left(\dfrac{\ln\left(\dfrac{x}{\tan(x)}\right)}{\tan^2(x)}\right)\)
Now, since the exponential function is continuous at 0, we can write
\(\displaystyle L = \lim_{x\to0} \exp\left(\dfrac{\ln\left(\dfrac{x}{\tan(x)}\right)}{\tan^2(x)}\right) = \exp\left(\lim_{x\to0}\dfrac{\ln\left(\dfrac{x}{\tan(x)}\right)}{\tan^2(x)}\right)\)
Let M denote the remaining limit.
We have \(\dfrac x{\tan(x)}\to1\) as \(x\to0\), so \(\ln\left(\dfrac x{\tan(x)}\right)\to0\) and \(\tan^2(x)\to0\). Apply L'Hopital's rule:
\(\displaystyle M = \lim_{x\to0}\dfrac{\ln\left(\dfrac{x}{\tan(x)}\right)}{\tan^2(x)} \\\\ M = \lim_{x\to0}\dfrac{\dfrac{\tan(x)-x\sec^2(x)}{\tan^2(x)}\times\dfrac{\tan(x)}{x}}{2\tan(x)\sec^2(x)}\)
Simplify and rewrite this in terms of sin and cos :
\(\displaystyle M = \lim_{x\to0} \dfrac{\dfrac{\tan(x)-x\sec^2(x)}{\tan^2(x)}\times\dfrac{\tan(x)}{x}}{2\tan(x)\sec^2(x)} \\\\ M= \lim_{x\to0}\dfrac{\sin(x)\cos^3(x) - x\cos^2(x)}{2x\sin^2(x)}\)
As \(x\to0\), we get another 0/0 indeterminate form. Apply L'Hopital's rule again:
\(\displaystyle M = \lim_{x\to0} \frac{\sin(x)\cos^3(x) - x\cos^2(x)}{2x\sin^2(x)} \\\\ M = \lim_{x\to0} \frac{\cos^4(x) - 3\sin^2(x)\cos^2(x) - \cos^2(x) + 2x\cos(x)\sin(x)}{2\sin^2(x)+4x\sin(x)\cos(x)}\)
Recall the double angle identity for sin:
sin(2x) = 2 sin(x) cos(x)
Also, in the numerator we have
cos⁴(x) - cos²(x) = cos²(x) (cos²(x) - 1) = - cos²(x) sin²(x) = -1/4 sin²(2x)
So we can simplify M as
\(\displaystyle M = \lim_{x\to0} \frac{x\sin(2x) - \sin^2(2x)}{2\sin^2(x)+2x\sin(2x)}\)
This again yields 0/0. Apply L'Hopital's rule again:
\(\displaystyle M = \lim_{x\to0} \frac{\sin(2x)+2x\cos(2x)-4\sin(2x)\cos(2x)}{2\sin(2x)+4x\cos(2x)+4\sin(x)\cos(x)} \\\\ M = \lim_{x\to0} \frac{\sin(2x) + 2x\cos(2x) - 2\sin(4x)}{4\sin(2x)+4x\cos(2x)}\)
Once again, this gives 0/0. Apply L'Hopital's rule one last time:
\(\displaystyle M = \lim_{x\to0}\frac{2\cos(2x)+2\cos(2x)-4x\sin(2x)-8\cos(4x)}{8\cos(2x)+4\cos(2x)-8x\sin(2x)} \\\\ M = \lim_{x\to0} \frac{4\cos(2x)-4x\sin(2x)-8\cos(4x)}{12\cos(2x)-8x\sin(2x)}\)
Now as \(x\to0\), the terms containing x and sin(nx) all go to 0, and we're left with
\(M = \dfrac{4-8}{12} = -\dfrac13\)
Then the original limit is
\(L = \exp(M) = e^{-1/3} = \boxed{\dfrac1{\sqrt[3]{e}}}\)
which orded pair is a solution of the equation 2x+4y=6x-y
Answers
Find a system of two equations in two variables, x1 and x2, that has the solution set given by the parametric representation
x1 = t and x2 = 7t − 8,
where t is any real number. (Enter your answer as a comma-separated list of equations.)
Let x2 = t, then x1 = ?
Answers
Answer:
3
Step-by-step explanation:
this is what I think
Find m∠2 if m∠4 = 130°.

Answers
m = 130 degrees
What is the common factor in 5w + 10w?
10w
15w
w
10
Answers
\(\huge\text{Hey there!}\)
\(\large\text{All you have to do is COMBINE your LIKE TERMS}\)
\(\large\text{5w + 10w}\)
\(\large\text{(5w + 10w) = 15w}\)
\(\boxed{\boxed{\large\text{Answer: \bf{15w}}}}\huge\checkmark\)
\(\text{Good luck on your assignment and enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\):)
Jamal wrote the inequality x/16 <6 . Which situation best represented by this inequality Helpppppp
Answers
Given problem;
Inequality equation;
\(\frac{x}{16}\) < 6
Before we solve, let us first translate this problem.
It simply states that for what value(s) of x will the expression be less than 6.
To find this value, we can simply carry out the normal mathematical simplification.
Simply multiply both sides by 16 to reduce the fraction;
16 x (\(\frac{x}{16}\)) < 6 x 16
On the left hand side, 16 will cancel out;
x < 96
Any value for which x is less than 96 will make the solution of this problem less than 6.
For example, 95;
\(\frac{95}{16}\) = 5.93
This value is less than 6
The sum of ten and the quotient of a number x and 6 please help !
Answers
Answer:
10 + x/6
Step-by-step explanation:
10 + x/6 represents this phrase
The negative sqaure root 75 fall between which consecutive integers.
Answers
Answer:
8 and 9
Step-by-step explanation
PLEASE HELP!!!
Find the common difference for the arithmetic sequence. -55, -50, -45, -40.....
Answers
Answer:
5
Step-by-step explanation:
Just grap any two consecutive terms in the sequence. lets say -55 and -50
-50-(-55) = 5
you can check this by picking two other terms
Please see attahed…………………….

Answers
Answer:
The graph is constant from (-oo,-2)U(4,oo).
The graph is increasing from (-2,4).
The graph never decreases.
Step-by-step explanation:
Take the x values from when the line is constant (not rising or falling), increasing (rising), and decreasing (falling).
oo means infinity
The graph is constant from (-oo,-2)U(4,oo).
The graph is increasing from (-2,4).
The graph never decreases.
A car travels 125 miles in 2 hours. At the same rate, how far would it travel in 5 hours?
Answers
Answer: 312.5 miles
Step-by-step explanation:
125/2 = 62.5 per hour x 5 hours = 312.5 miles
help please ill give you brainliest !! and show work please
find the length of SEGMENT BC

Answers
Answer:
BC = 4
Step-by-step explanation:
The diagram shows a circle with radius AE and chord BD.
Assuming that the radius bisects the chord, then AE is perpendicular to BD. So the measure of angle ACB is 90°.
This means that triangle ACB is a right triangle, with legs AC and BC, and hypotenuse AB.
The length of the radius is:
\(AE = 3 + 2 = 5\)
As AB is also the radius, AB = 5.
To find the length of BC, use Pythagoras Theorem:
\(AC^2+BC^2=AB^2\)
\(3^2+BC^2=5^2\)
\(9+BC^2=25\)
\(9+BC^2-9=25-9\)
\(BC^2=16\)
\(\sqrt{BC^2}=\sqrt{16}\)
\(BC=4\)
Therefore, the length of line segment BC is 4.
What is the data correlation in the scatter plot below?
No correlation
Positive
Negative

Answers
The data correlation in the scatter plot above include the following: B. positive.
What is a positive correlation?In Mathematics, a positive correlation is used to described a scenario in which two variables move in the same direction and are in tandem.
This ultimately implies that, a positive correlation exist when two variables have a linear relationship or are in direct proportion. Therefore, when one variable increases, the other variable generally increases, as well.
By critically observing the scatter plot shown in the image attached above, we can reasonably infer and logically deduce that there is a positive correlation between the x-values and y-values because they both increase simultaneously.
Read more on positive correlation here: brainly.com/question/3753830
#SPJ1
Jen has three bracelets each bracelet has seven diamonds how many diamonds does Jen have in all 
Answers
Answer:
21 diamonds.
Step-by-step explanation:
1 bracelet = 7 diamonds
3 bracelet= ? diamonds
All we have to do is multiply 3 by 7 to get the number of diamonds Jen have with three bracelets.
3 x 7 = 21
Answer:
1 bracelet has 7 diamonds, therefore 2 has 14 and 3 has 21 diamonds
Step-by-step explanation:
A building is constructed using bricks that can be modeled as right rectangular prisms with a dimension of 7 in by 3 in by 3 1/4 in. If the bricks cost $0.04 per cubic inch, find the cost of 650 bricks. Round your answer to the nearest cent.
Answers
The cost of 650 bricks which are right rectangular prisms is $1774.5.
What is a rectangular prism?
Having six faces, a rectangular prism is a three-dimensional shape (two at the top and bottom and four are lateral faces). The prism's faces are all rectangular in shape. There are three sets of identical faces as a result. A rectangular prism is often referred to as a cuboid because of its shape.
The dimensions of the right rectangular prism brick is -
width, w = 7 in
length, l = 3 in
height, h = 3(1/4) in = 3.25 in
Find the volume of the brick -
Volume = w × l × h
Volume = 7 × 3 × 3.25
Volume = 68.25 in³
The volume occupied by 650 bricks is -
V650 = 68.25 × 650
V650 = 44362.5 in³
The cost of cubic inch of brick is $0.04.
The cost of 650 bricks is -
Total cost = 44362.5 in³ × $0.04
Total cost = $1774.5
Therefore, the total cost is obtained as $1774.5.
To learn more about rectangular prism from the given link
https://brainly.com/question/24284033
#SPJ1
In ∆BCD if BC=BD, m<B=(13x-35)°, m<C=(5x-19)°, and m<D=(2x+14)°, find x and the measure of each angle
Answers
Answer:
Value of x = 11 ° , ∠B = 108° ,∠C = 36° ,∠D = 36°
Step-by-step explanation:
Given :
In ΔBCD , BC = BD And ∠B= (13x-35)° , ∠C= (5x-19)° ,∠D=(2x+14)°
To Find :
value of x and ∠D , ∠B and ∠C
Solution:
∵ BC=BD , So ∠C = ∠D
Therefore 5x-19 = 2x+14
3x = 33 , ∴ x=11°
So, ∠B = (13×11) - 35 = 108°
∠C = (5×11)-19 = 36°
∠D= (2×11) +14 =36°
What is the volume of a triangular pyramid that is 10 in. tall and has a base area of 9 square in.?

Answers
Step-by-step explanation:
anewer is 30 cubic inches.

HELPPPPPPP PLEASEEEEE WILL GIVE BRAINLEST

Answers
So thats the answer for your MATCHEMATIC QUESTIONSS
Preciso de ajudaa! Resolução também! - Considere as funções f e g tais que f(x)= x³+1 e g(x)= x-2 Determine: a)(fog)(0) b)(gof)(0) c)(fof)(1) d)(gog)(1)
Answers
Answer:
(fog)(x) means that we have the function f(x) evaluated in the function g(x), or f(g(x)).
So, if f(x) = x^3 + 1 and g(x) = x - 2.
we have:
a) (fog)(0) = f(g(0)) = (0 - 2)^3 + 1 = -8 + 1 = -7
b) (gof)(0) = g(f(0)) = (0^3 + 1) - 2 = -1
c) (fof)(1) = f(f(1)) = (1^3 + 1)^3 + 1 = 2^3 + 1 = 8 + 1 = 9
d) (gog)(1) = g(g(1)) = (1 - 2) - 2 = -1 -2 = -3
calcule el cociente de los siguientes ejercicios
(-8)/(+2)
Answers
Answer:
-4
Step-by-step explanation:
A cone and a cylinder have the same radius and height. The volume of the cone is 100 pi cubic feet. what is the volume of the cylinder
Answers
The volume of the cylinder is equal to 300π cubic feet.
What is meant by volume?
Volume is the measure of space within a particular 3D object in mathematics. For instance, a fish tank measures three feet long by one foot wide by two feet high. The volume is calculated by multiplying the length, the breadth, and the height, or 3x1x2, which equals six. The fish tank, therefore, has a 6 cubic foot volume.
It is given that the radius and height of the cone and cylinder are the same.
The volume of the cone is 100π cubic feet.
The volume of a cone is \(\frac{1}{3} \pi r^{2} h=100\pi\)
The volume of a cylinder is \(\pi r^{2}h\).
Therefore the volume of a cylinder is 3 times the volume of a cone with the same radius and height.
Therefore the volume of the cylinder is equal to 300π cubic feet.
To learn more about the volume of the cone and cylinder, refer to the link below:
brainly.com/question/26263468
#SPJ1