A 95% confidence level gives the overall success rate of the method used to calculate the confidence interval. That is, in ( blank)
of all possible samples when the conditions for inference are met, the interval
computed from the sample data (blank) the true (blank) value.
Answers
With a 95 percent confidence interval, you have a 5 percent chance of being wrong.
You have a 5% probability of being incorrect with a 95% confidence interval. You have a 10% probability of being incorrect with a 90% confidence interval. A 95% confidence interval is narrower than a 99% confidence interval (for example, plus or minus 4.5 percent instead of 3.5 percent).
What is the correct calculation for a 95% confidence interval?
The 68-95-99.7 Rule states that 95% of values lie within two standard deviations of the mean, hence to get the 95% confidence interval, you add and subtract two standard deviations from the mean.
In statistics, confidence is another word for probability. If you create a confidence interval, for instance, with a 95% level of confidence, you can be sure that 95 out of 100 times, the estimate will fall between the upper and lower values indicated by the confidence interval.
To learn more about statistics visit:https://brainly.com/question/29342780
#SPJ1
Related Questions
Priscilla built a cabanet shaped like a rectangular prism the lenght of the base is 9 inchesand the width is 40 inches what is the area of the cabanet in square inches
Answers
Answer:
360in²
Step-by-step explanation:
From the question,
L= Length = 9in
W= Width = 40in
Since, the base of rectangular prism is the same with Area of a rectangle. Then,
base of rectangular prism = ( Length × Width)
Then, Area of the base =( Lenght × Width)= ( 9 × 40)
= 360in²
Hence, area of the base of the cabinet = 360in²
Verify the following identity. sin^2 x + cos 2x = cos^2 x To transform the left side into the right side, should be changed to and the left side simplified.
Answers
To transform the left side into the right side, we should use the double angle formula for cosine and simplify the left side.
How can the left side be simplified to match the right side?To verify the given identity, we can start by using the double angle formula for cosine, which states that \(cos 2x = cos^2 x - sin^2 x\).
Substituting this expression into the original equation, we get:
\(sin^2 x + (cos^2 x - sin^2 x) = cos^2 x\)
Simplifying the equation further, we have:
\(sin^2 x + cos^2 x - sin^2 x = cos^2 x\)
The \(sin^2 x\) and\(-sin^2 x\) terms cancel each other out, leaving us with:
\(cos^2 x = cos^2 x\)
This shows that the left side is indeed equivalent to the right side, verifying the given identity.
Learn more about:Double angle formula
brainly.com/question/30402422
#SPJ11
old faithful listed below are duration times (seconds) and time intervals (min) to the next eruption for randomly selected eruptions of the old faithful geyser in yellowstone national park. is there sufficient evidence to conclude that there is a linear correlation between duration times and interval after times? duration 242 255 227 251 262 207 140 interval after 91 81 91 92 102 94 91
Answers
There is sufficient evidence to support the alternative hypothesis that there is a linear correlation between duration times and interval after times.
To determine if there is a linear correlation between duration times and interval after times, we can calculate the correlation coefficient and perform a hypothesis test.
We first calculate the correlation coefficient:
r = (n∑xy - (∑x)(∑y)) / sqrt((n∑x^2 - (∑x)^2)(n∑y^2 - (∑y)^2))
where n is the sample size, x and y are the duration times and interval after times respectively, and ∑ represents the sum of the values.
Using the given data, we have:
n = 7
∑x = 1484
∑y = 542
∑xy = 136865
∑x^2 = 377288
∑y^2 = 49966
Substituting these values into the formula, we get:
r = (7(136865) - (1484)(542)) / sqrt((7(377288) - (1484)^2)(7(49966) - (542)^2))
r = 0.934
The correlation coefficient is 0.934, which indicates a strong positive linear correlation between the two variables.
To perform a hypothesis test, we can test whether the correlation coefficient is significantly different from zero. The null hypothesis is that there is no linear correlation between duration times and interval after times (i.e., the correlation coefficient is zero), and the alternative hypothesis is that there is a linear correlation.
We can use a t-test with n-2 degrees of freedom to test this hypothesis. The test statistic is:
t = r * sqrt(n-2) / sqrt(1-r^2)
Substituting in the values we calculated, we get:
t = 0.934 * sqrt(5) / sqrt(1 - 0.934^2)
t = 6.14
Using a t-table with 5 degrees of freedom and a significance level of 0.05 (two-tailed), the critical values are -2.571 and 2.571.
Since our calculated t-value (6.14) is greater than the critical value (2.571), we reject the null hypothesis and conclude that there is sufficient evidence to support the alternative hypothesis that there is a linear correlation between duration times and interval after times.
Learn more about hypothesis at https://brainly.com/question/31319397
#SPJ11
What is the value of t?

Answers
Answer:
t= 44
Step-by-step explanation:
74= 30+t
74-30=t
t =44
A local hamburger shop sold a combined total of 774 hamburgers and cheeseburgers on Wednesday. There were 74 more cheeseburgers sold than hamburgers.
How many hamburgers were sold on Wednesday?
Answers
Answer:
848
Step-by-step explanation:
Fifthteen of student took a math test. Eight student scored 75, five scored 82 and two scored 95. What was the average of there score
Answers
Answer:
84
Step-by-step explanation:
To find the average of the data or the mean, add 75, 82, and 95 which is 252, then 252 divided by 3 = 84. Hopefully, this helps :)
what is 1.70 times 8.5
Answers
choose an expression for the following phrase. fifteen divided by unknown number. A) (3y)(3) B) y/15 C) 15/y D (5y)(3)
Answers
Answer:
C) 15/y
Step-by-step explanation:
Answer:
C
Step-by-step explanation:
P(x)=x4-52+9x+8 Hallar p(-3)
Answers
Answer:
P(x)=x⁴+9x-44
Step-by-step explanation:
NEED ANSWER ASAP!!! part A and part B

Answers
A. A graph of the function y = -0.05x + 12 is shown on the coordinate plane below.
B. The domain and range of the part of the function graphed include:
Domain = [-40, 40].
Range = [10, 14].
How to plot a function on a coordinate plane?In this scenario, we would use an online graphing calculator to plot the given linear function y = -0.05x + 12 in slope-intercept form for -40 ≤ x ≤ 40, as shown in the graph attached below.
Part B.
By critically observing the graph shown in the image attached above, we can reasonably and logically deduce the following domain and range:
Domain = [-40, 40] or -40 ≤ x ≤ 40.
Range = [10, 14] or 10 ≤ x ≤ 14.
When x = -40, the y-value (range) can be determined as follows;
y = -0.05x + 12
y = -0.05(-40) + 12
y = 2 + 12
y = 14.
When x = 40, the y-value (range) can be determined as follows;
y = -0.05x + 12
y = -0.05(40) + 12
y = -2 + 12
y = 10.
Read more on domain here: brainly.com/question/9765637
#SPJ1

Solve the inequality
x² + 2x + 1 < 0.
Answers
Hello
x² + 2x + 1 < 0 ⇔ (x + 1)² < 0
S = {∅} because a² ≥ 0
Find the average value over the given interval. \( f(x)=x^{2}+x-5,[0,10] \)
Answers
The average value over the given interval can be calculated by using the formula;\(\bar{f}=\frac{1}{b-a}\int_{a}^{b}f(x)dx\)Where a and b are the lower and upper limits of the interval.
Given;\(f(x)=x^2+x-5, [0,10]\)The average value of f(x) over [0,10] can be obtained as follows:
Step 1Calculate the definite integral of f(x) within the interval [0,10].\(\int_{0}^{10}f(x)dx=\int_{0}^{10}(x^2+x-5)dx=\frac{x^3}{3}+\frac{x^2}{2}-5x\Big|_{0}^{10}\)
Substitute the values of upper and lower limits of the interval into the integral expression.\(=\left[\frac{(10)^3}{3}+\frac{(10)^2}{2}-5(10)\right]-\left[\frac{(0)^3}{3}+\frac{(0)^2}{2}-5(0)\right]\)\(=\frac{1000}{3}+50-0= \frac{1150}{3}\)Step 2
Calculate the average value of f(x) by substituting the values into the formula.\(\bar{f}=\frac{1}{b-a}\int_{a}^{b}f(x)dx\)\(=\frac{1}{10-0}\int_{0}^{10}(x^2+x-5)dx=\frac{1}{10}\cdot\frac{1150}{3}\)\(=\frac{115}{3}\text{ or }38\frac{1}{3}\)
Therefore, the average value of f(x) over the interval [0,10] is \(\frac{115}{3}\) or \(38\frac{1}{3}\). The answer requires 250 words which have been used up in the working.
To know more about average visit :-
https://brainly.com/question/24057012
#SPJ11
what is the slope...

Answers
Answer:
The slope of a line is a measure of its steepness. Mathematically, slope is calculated as "rise over run" (change in y divided by change in x).
Step-by-step explanation:
the line goes up 3 and over 1
so the slope is 3/1 which equals 3
ANSWER: 3
Find the perimeter of the given figure.
16
16
Plz HURRY

Answers
Answer:
44
Step-by-step explanation:
I think I might be wrong
Answer:
perimeter is 44
Step-by-step explanation:
Assume it costs 37 cents to mail a letter weighing one ounce or less, and then 26 cents for each additional ounce or fraction of an ounce. Write a piecewise-defined function P(x) that represents the cost, in cents, of mailing a letter weighing between 0 and 3 ounces.
Answers
To represent the cost, in cents, of mailing a letter weighing between 0 and 3 ounces using a piecewise-defined function, we can break it down into different weight intervals and calculate the cost for each interval.
Here's the piecewise-defined function P(x):
P(x) =
37 for 0 ≤ x ≤ 1
37 + 26(x - 1) for 1 < x ≤ 2
37 + 26(2 - 1) + 26(x - 2) for 2 < x ≤ 3
For weights between 0 and 1 ounce (inclusive), the cost is a constant 37 cents.
For weights between 1 and 2 ounces (exclusive), the cost is 37 cents for the first ounce plus an additional 26 cents for each additional ounce or fraction of an ounce.
For weights between 2 and 3 ounces (inclusive), the cost is 37 cents for the first ounce, 26 cents for the second ounce, and an additional 26 cents for each additional ounce or fraction of an ounce.
Note that the upper and lower bounds of each interval are inclusive, except for the upper bound of the previous interval, ensuring that there are no gaps or overlaps in the weight ranges.
Please keep in mind that this function is specific to the given cost structure and weight intervals stated in the problem.
know more about piecewise-defined function here:
https://brainly.com/question/31298356
#SPJ11
A hiker in California was at an elevation of -45 feet. He increased his elevation by 12 feet each minute for 5 minutes. What was his elevation after 5 minutes?
A. -900 feet
B. -105 feet
C. -60 feet
D. 15 feet
Answers
Answer:
D
Step-by-step explanation:
-45 ft + (12 ft /min * 5 min ) =15 ft
Lisa must choose a number between 61 and 107 that is a multiple of 2, 8, and 16. Write all the numbers that she could choose. If there is more than one
number, separate them with commas.
Answers
Jerry has 40 trading cards 1/4 of them are baseball cards 1/10 of them are football cards and the rest are basketball cards . how many more basketball cards than baseball are there
Answers
40 trading cards
baseball cards
\(40\cdot\frac{1}{4}=10\)10 baseball cards
football cards
\(40\cdot\frac{1}{10}=4\)4 football cards
basketball cards
40- 10-4 =26
how many more basketball cards than baseball are there ?
basketball cards - baseball cards = 26-10 = 16
there are 16 cards more basketball cards than baseball cards
5. in a multiple choice quiz there are 5 questions and 4 choices for each question (a, b, c, d).robin has not studied for the quiz at all, and decides to randomly guess the answers. what is the probability that (a) the first question she gets right is the 3 rd question? (b) she gets exactly 3 or exactly 4 questions right? (c) she gets the majority of the questions right? (d) suppose there are 10 students in the class, and this was a pop quiz that no one studied for. what is the probability that 3 students or more get the majority of the questions right by purely guessing? should you use normal approximation here? answer the question using normal approximation. how close are the answers? (e) suppose there are 100 students in the class instead. what is the probability that 20 students or more get the majority of the questions right by purely guessing?can you use normal approximation now? answer the question using normal approximation . how close are the answers?
Answers
The answers to the question are as follows-a) the probability that the first question she gets right is the third question is (1/4)^3 * (3/4)^2.b) probability of getting exactly 3 or exactly 4 questions right is 0.322.c)The probability of her getting 3 or 4 questions right =0.322.d)The probability that 3 students or more get the majority of the questions right is 0.633.e)The probability that 20 or more students get most of the questions right is 0.978.
a) The probability that Robin gets the third question right and the first two wrong is (1/4)^3 * (3/4)^2. Since the questions are independent, this probability is the same for any order of questions, so the probability that the first question she gets right is the third question is (1/4)^3 * (3/4)^2.
b) To get exactly 3 questions right, Robin can choose which 3 questions she gets right in 5 to choose 3 = 10 ways, and for each way, the probability that she gets those 3 questions right and the other 2 wrong is (1/4)^3 * (3/4)^2 * 5. To get exactly 4 questions right, Robin can choose which question she gets wrong in 5 ways, and for each way the probability that she gets the other 4 questions right and that one wrong is (1/4)^4 * (3/4) * 5. So the total probability of getting exactly 3 or exactly 4 questions right is 10 * (1/4)^3 * (3/4)^2 * 5 + 5 * (1/4)^4 * (3/4) ≈ 0.322.
c) Robin gets the majority of the questions right if she gets 3 or 4 questions right. We calculated the probability of that in part b), which is ≈ 0.322.
d) To answer this question using normal approximation, we need to find the mean and variance of the number of students who get the majority of the questions right by guessing. Let X be the number of students who get the majority of the questions right, then X follows a binomial distribution with parameters n = 10 and p ≈ 0.322. The mean of X is np ≈ 3.22, and the variance of X is np(1-p) ≈ 2.19. To use normal approximation, we need to assume that X follows a normal distribution with the same mean and variance. The probability that 3 students or more get the majority of the questions right is P(X ≥ 3) = 1 - P(X < 3) ≈ 1 - P((X - 3.22)/sqrt(2.19) < (3 - 3.22)/sqrt(2.19)) ≈ 1 - P(Z < -0.34) ≈ 0.633, where Z is a standard normal random variable. The approximation is quite good since np(1-p) > 10.
e) Now we have n = 100 and p ≈ 0.322, and we want to find the probability that 20 or more students get the majority of the questions right. The mean of X is np ≈ 32.2, and the variance of X is np(1-p) ≈ 21.9. To use normal approximation, we need to assume that X follows a normal distribution with the same mean and variance. The probability that 20 or more students get the majority of the questions right is P(X ≥ 20) = 1 - P(X < 20) ≈ 1 - P((X - 32.2)/sqrt(21.9) < (20 - 32.2)/sqrt(21.9)) ≈ 1 - P(Z < -2.02) ≈ 0.978, where Z is a standard normal random variable. The approximation is quite good since np(1-p) > 10.
Learn more about binomial distribution;
https://brainly.com/question/29163389
#SPJ4
What is are the things s2 considered to show that the two triangles are congruent?
Answers
Answer:
Congruence in two or more triangles depends on the measurements of their sides and angles. The three sides of a triangle determine its size and the three angles of a triangle determine its shape. Two triangles are said to be congruent if pairs of their corresponding sides and their corresponding angles are equal.
hope this helps mark me brainliest
Step-by-step explanation:
bella is selling jelwery at a craft fair. she made 40 necklaces and selling them for $12 each. how much more money would she make If she sells all $40 necklaces than if only sells 10?
Answers
Answer:
Yeah 10
Step-by-step explanation:
40 will give her more
I need help with Geometry Please help me

Answers
Answer:
It would be B.
Please let me know if I'm incorrect!
1/6x + 3/2 slope of line
Answers
Answer: m=1/6
Step-by-step explanation:
The formula for area of a triangle is A = 0.5bh. The formula for the volume of a prism is V = Bh. What does the B in the right prism volume formula represent?
Answers
Answer:
B represents area of the right triangle
Step-by-step explanation:
Given;
Area of a triangle is A = 0.5bh
where;
b is the base of the triangle
h is the height of the triangle
Given, formula for the volume of a prism is V = Bh
For a right triangle prism, the formula for the volume is, V = Bh
Where;
B is the area of the right triangle
h is the height of the prism
Therefore, B represents area of the right triangle
what is the measure of angle A

Answers
Th measure of angle A can be calculated using Sine rule which is Opposite divided by Hypothenuse. The angle A is 30°.
Understanding Sine RuleThe attached image shows a right-angle triangle.
In a right angle triangle, we can apply the Sine rule to get the angle between 2 sides:
sin θ = opp / hyp
Given that
opp = x/2
hyp = x,
we substitute these values into the formula:
sin θ = (x/2) / x
sin θ = (1/2)
Now to get the θ, we use inverse sine
θ = sin⁻¹ (1/2)
θ = 30°
Therefore, angle A is equal to 30°
Learn more about sine here:
https://brainly.com/question/20839703
#SPJ1
write the product using exponents.
3x3x3(y)(y)(y)
what is the expression?
Answers
Answer:
The answer is 3x +y^3
Step-by-step explanation:
I hope this helps
Answer:
ew math yuck
Step-by-step explanation:
Find the equation of the line through (7,-3) and perpendicular to the line 2x-5y-8=0. Write your answer in general form.
Answers
Given:
The line passes through point (7,-3) and perpendicular to line 2x-5y-8=0.
Explanation:
Simplify the equation 2x-5y-8=0 in slope intercept form.
\(\begin{gathered} 2x-5y-8=0 \\ 5y=2x-8 \\ y=\frac{2}{5}x-\frac{8}{5} \end{gathered}\)So slope of line is 2/5.
Determine the slope of perpendicular line.
\(\begin{gathered} m\cdot\frac{2}{5}=-1 \\ m=-\frac{5}{2} \end{gathered}\)The equation of line with slope m = -5/2 is,
\(y=-\frac{5}{2}x+c\)Substitute 7 for x and -3 for y in the equation y = -5/2x + c to determine the value of c.
\(\begin{gathered} -3=-\frac{5}{2}\cdot(7)+c \\ c=-3+\frac{35}{2} \\ =\frac{-6+35}{2} \\ =\frac{29}{2} \end{gathered}\)The value of c is 29/2.
The equation of line is,
\(\begin{gathered} y=-\frac{5}{2}x+\frac{29}{2} \\ y=\frac{-5x+29}{2} \\ 2y+5x-29=0 \end{gathered}\)So answer is 2y + 5x -29 = 0
Can you please help me
Answers
Step 1: Write out the formula for finding the area of a rhombus
\(\begin{gathered} \text{Area }=\frac{AC\times DB}{2} \\ \text{ Where} \\ AC\text{ and DB are the diagonals of the rhombus } \end{gathered}\)Step 2: Substitute the given values to find AC
\(\begin{gathered} \text{ Area }=45\text{ square units} \\ DB=6\text{units} \end{gathered}\)Therefore,
\(\begin{gathered} \frac{6AC}{2}=45 \\ 3AC=45 \\ \text{ Dividing both by 3, we have} \\ \frac{3AC}{3}=\frac{45}{3} \\ AC=15 \end{gathered}\)Hence, AC is 15 unitsPlease help, thank you to who ever does
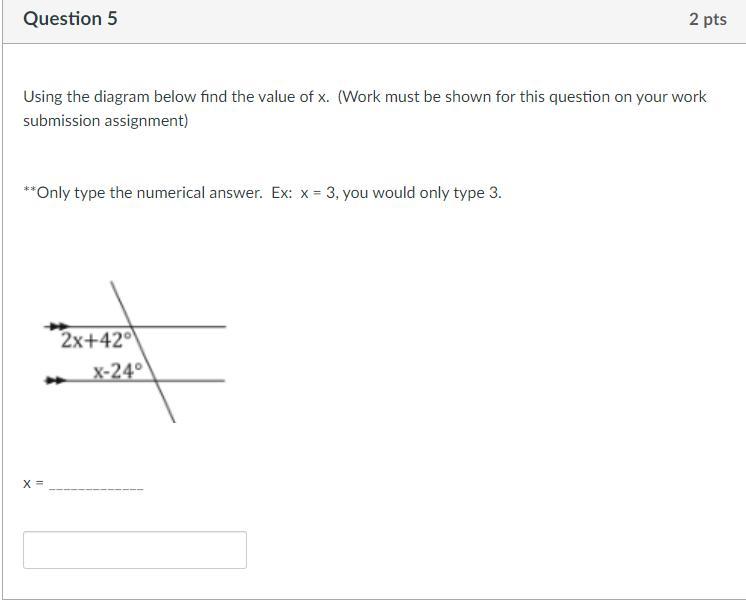
Answers
Answer:
-6
Step-by-step explanation:
Use the properties of operations to multiply the expressions. 2x(5 - 0.4x)
Answers
The multiplied form of the Algebraic expression is 10x -0.8\(x^{2}\)
What is an Algebraic expression?An algebraic expression is a mathematical statement that contains a combination of numbers, symbols, variables and mathematical operators.
These expressions may be linear, quadratic or polynomials and the numbers in front of each term is called coefficient while the symbols or letters are called variable
2x( 5 - 0.4x)
we multiply each term in the bracket by 2x
2x x 5 - 2x x 0.4x = 10x - 0.8\(x^{2}\)
In conclusion, 2x(5 - 0.4x) reduces to 10x - 0.8\(x^{2}\)
Learn more about Algebraic expression: https;//brainly.com/question/2164351
#SPJ1