a) 4
If the perimeter of this figure is 62 what is the value of x?
A.) 4
B.) -4
C.) -7
D.) 7

Answers
Answer:
i think c
Step-by-step explanation:
Related Questions
need the answer to this asap

Answers
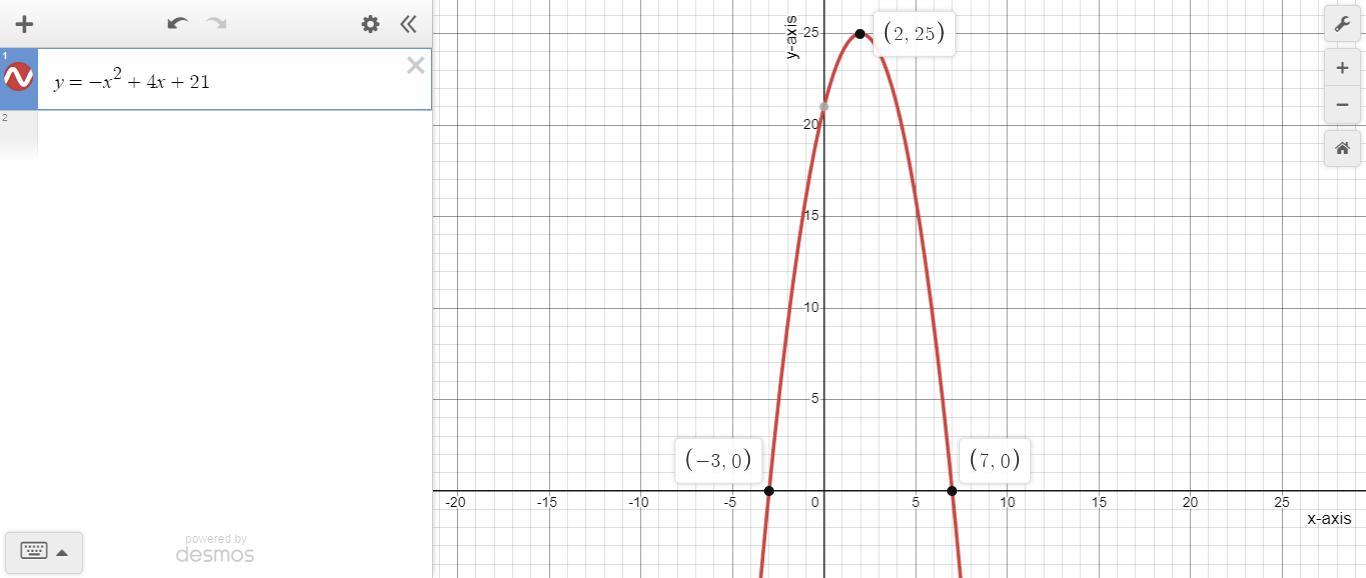
A graph that represent the quadratic equation y = -x² + 4x + 21 is shown in the image attached below.
What is the graph of a quadratic function?In Mathematics and Geometry, the graph of a quadratic function would always form a parabolic curve because it is a u-shaped. Based on the given quadratic function, we can logically deduce that the graph would be a downward parabola because the coefficient of x² is negative and the value of "a" is lesser than zero (0).
Since the leading coefficient (value of a) in the given quadratic function y = -x² + 4x + 21 is negative 1, we can logically deduce that the parabola would open downward and the solution would be represented by the following x-intercepts (zeros or roots);
Ordered pair = (-3, 0)
Ordered pair = (0, 7)
Read more on quadratic functions here: brainly.com/question/29499209
#SPJ1
Consider this triangle.

Answers
use sin
sin(50) = x/6
sin(50) x 6 = x
x = ~4.5963
please help
One side of a triangle is 1 inch longer than the shortest side and is 1 inch shorter than the longest side. The perimeter is 17 inches. Find the dimensions of the triangle.
Answers
Answer: \(4\frac{2}{3} in;\) \(5\frac{2}{3} in;\) \(6\frac{2}{3} in\)
I need the answer to this question I don’t understand it

Answers
This would be y=3/1x-3
Explanation:
They give you three points so just do rise over run. As u can see in order to get to the next point you would have to go up 3 and 1 to the right. For the y intercept you can see that the line passes -3 .
Hope this helps lmk if I’m right!!
For part of the first year of a dog's life, its growth can be
approximated using a linear function. Emilie has two puppies:
a Border collie and a younger Saint
Bernard. During a 4-week period,
the Border collie grows from
13.4 kg to 17 kg, while the Saint
Bernard
grows from 6 kg to 12.4 kg.
Suppose each dog grows at a
constant rate. Will the dogs
ever have the same mass? If
so, approximately what is
the mass?
Answers

\((5-\sqrt{5}) and (\sqrt{5} -5)\)Are two roots of a fourth degree polynomial with integer coefficients, what are the other roots?
Answers
Answer:
(5 +√5) and (-√5 -5)
Step-by-step explanation:
Given two roots of the 4th-degree polynomial with integer coefficients are (5-√5) and (√5-5), you want to know the other two roots.
ConjugatesThe other two roots are the conjugates of the given roots. That is, the signs of the √5 term will change:
(5 +√5) and (-√5 -5)
__
Additional comment
The polynomial is x⁴ -60x² +400.
 and (\sqrt{5} -5)[/tex]Are two roots of a fourth degree polynomial with integer coefficients,](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/EGuFX1SpVwCYny0abTM7rz3QFWZBVb2G.png)
A traffic engineering study on traffic delay was conducted at intersections with signals on urban streets. Three types of traffic signals were utilized in the study: (1) pretimed, (2) semi-actuated, and (3) fully actuated. Five intersections were used for each type of signal. The measure of traffic delay used in the study was the average stopped time per vehicle at each of the intersections (seconds/vehicle). The data follow Pretimed Semi-actuated Fully actuated 36.6 17.5 15.0
39.2 20.6 10.4
30.4 18.7 18.9
37.1 25.7 10.5 34.1 22.0 15.2 Source: W. Reilly, C. Gardner, and J. Kell (1976). A technique for measurement of delay at intersections. Technical Report FHWA-RD-76- 135, Federal Highway Administration, Office of R &D, Washington, D.C. Use the data from Exercise 1 to determine how many intersections the traffic engineer would need for each type of traffic signal to reject the null hypothesis at the .01 level of significance witha power of .90 if mean delays at the three traffic signal types were 20, 18, and 16 seconds, respectively.
Answers
The average number of intersections the traffic engineer would need for each type of traffic signal to reject the null hypothesis at the 0.01 level of significance with a power of 0.90 is six
To test the effectiveness of these signals, the engineer must reject the null hypothesis, which states that there is no significant difference in the mean delays between the three types of signals. The engineer wants to reject the null hypothesis at the 0.01 level of significance with a power of 0.9. In other words, they want to be 90% sure that they can detect a significant difference if it exists.
Using the data provided in the study, the engineer can calculate the sample size needed for each type of signal. They need at least five intersections for pretimed signals, six intersections for semi-actuated signals, and four intersections for fully actuated signals to reject the null hypothesis at the desired level of significance with a power of 0.9.
To know more about average here
https://brainly.com/question/16956746
#SPJ4
what is the measure of the missing angle

Answers
Answer:
82.1
Step-by-step explanation:
a triangle will always be 180° so you add the numbers you have already and subtract them from the total
41.2 + 56.7 =97.9
180-97.9= 82.1
PLEASE HELP! 43 POINTS
Brenda invited 32 people to her graduation party. If each person will drink about 3 cups of punch, how many gallons of punch does Brenda’s mom need to buy?
How many quarts is this equal to?
Answers
Answer:
1 gallon = 16 cups
3 cups per person
32 people
32x3=96/16=6
she needs 6 gallons
Hi!! Can someone answer this question please & only list the coordinates, will be listing 5 more questions ❤️

Answers
Answer:
\( M(6, 6) \)
Step-by-step explanation:
Given:
Endpoints of a line segment, T(6, 3) and U(6, 9)
Required:
Midpoint, M, of line segment TU
✍️Solution:
Apply the midpoint formula, which is given as: \( M(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}) \).
Let:
\( T(6, 3) = (x_1, y_1) \)
\( U(6, 9) = (x_2, y_2) \)
Plug in the values into the formula
\( M(\frac{6 + 6}{2}, \frac{3 + 9}{2}) \)
\( M(\frac{12}{2}, \frac{12}{2}) \)
\( M(6, 6) \)
Coordinates of the midpoint, M, of line segment TU is \( (6, 6) \)
consider the following coefficient matrix, which contains a parameter, ∝.
x = (7/4 3/4)
(∝ 7/4) x
a) Determine the eigenvalues in terms of ∝
Enter your answers in increasing order.
r₁ =
r₂=
b)Find the critical value or values of ∝ where the qualitative nature of the phase portrait for the system changes.
Enter your answers in increasing order. If there is only one critical value, enter NA in the second answer region.
∝=
∝=
Answers
The eigenvalues in terms of α are (7 + sqrt(49 - 16α)) / 4 and (7 - sqrt(49 - 16α)) / 4, in increasing order. There are no critical values.
The given coefficient matrix is [[7/4, 3/4], [α, 7/4]]. To find the eigenvalues, we need to solve the characteristic equation det(A - λI) = 0, where A is the coefficient matrix, I is the identity matrix, and λ is the eigenvalue.
Expanding the determinant, we get:(7/4 - λ)(7/4 - λ) - (3/4)(α) = 0
Simplifying and rearranging, we get: λ^2 - (7/2)λ + (49/16) - (3/4)α = 0
Using the quadratic formula, we get: λ = (7 ± sqrt(49 - 16α)) / 4
Therefore, the eigenvalues in terms of α are (7 + sqrt(49 - 16α)) / 4 and (7 - sqrt(49 - 16α)) / 4, in increasing order.
To find the critical values of α where the qualitative nature of the phase portrait changes, we need to examine the sign of the eigenvalues. If both eigenvalues are real and have the same sign, the phase portrait consists of either a stable node or a stable spiral. If both eigenvalues are real and have opposite signs, the phase portrait consists of either a saddle or an unstable node. If both eigenvalues are complex conjugates with positive real part, the phase portrait consists of a stable focus, and if both eigenvalues are complex conjugates with negative real part, the phase portrait consists of an unstable focus.
From part a), we know that the eigenvalues are (7 + sqrt(49 - 16α)) / 4 and (7 - sqrt(49 - 16α)) / 4. To determine the critical values of α where the nature of the phase portrait changes, we need to set each eigenvalue equal to zero and solve for α.
Setting (7 + sqrt(49 - 16α)) / 4 = 0, we get sqrt(49 - 16α) = -7, which is not possible since the square root of a real number is always non-negative. Therefore, there are no critical values of α where the nature of the phase portrait changes. Alternatively, we can examine the sign of the discriminant, which is 49 - 16α. If the discriminant is positive, the eigenvalues are real and have opposite signs, indicating a saddle or an unstable node. If the discriminant is zero, one of the eigenvalues is zero, indicating a degenerate case. If the discriminant is negative, the eigenvalues are complex conjugates with non-zero real part, indicating a stable focus or a stable spiral. In this case, the discriminant is always positive or zero, since α can take any value. Therefore, there are no critical values of α where the nature of the phase portrait changes.
to learn more about eigenvalues, click: brainly.com/question/31650198
#SPJ11
1. What is the actual length of the truck?
1 cm = 1.7 feet
The gridlines are spaced 1 cm apart.
Answers
Answer:
20.4
Step-by-step explanation:
PLS HURRY!!!!!!!!!! NEED HELP

Answers
Answer:
42, 56, 70
Step-by-step explanation:
A right triangle must always have a ratio of side lengths that allow it to connect fully.
does anyone understand this x = 0.5, y = 1/10? help please!!!!
Answers
Answer:
x = 0.5
x-0.5=0
10x - 5 = 0
2x - 1 = 0
y=1/10
y - 1/10 = 0
10y - 1 = 0
Question in pic. Plz open the pic for the question ..corect gets branliest

Answers
Given: In Δ ABC and ΔAEC,
AB=BC and AD=CD
i) In ΔADB and CBD, we have
AD = DC [given]
AB=BC [given]
DB= DB [given]
⇒ ΔADB ≅ΔCDB [By SSS congruence rule]
⇒ ∠ADB ≅∠CDB ...(i) [Corresponding parts of congruent triangles are congruent]
Since AC is a straight line,
∠ADB+∠CDB = 180° [Linear pair]
⇒∠ADB+∠ADB=180° [from (i)]
⇒2 ∠ADB=180°
⇒∠ADB=90° =∠CDB
Also ∠ADB+∠ADE=180° [Linear pair]
⇒∠ADE=180°-∠ADB = 180°-90°
⇒∠ADE=90°, i.e. ∠ADE is a right triangle.
Similarly, ∠CDB+∠CDE=180°
⇒∠CDE=90°
ii) Now, in ΔADE and CDE
AD= CD [given]
ED=ED [Common]
∠ADE= ∠CDE = 90°
⇒ΔADE ≅ CDE [By SAS congruence rule ]
⇒AE=EC [Corresponding parts of congruent triangles are congruent]
Hence proved.
Show that A is an eigenvalue of A if and only if λ is an eigenvalue of AT. [Hint: Find out how A-A and AT-AI are related.]In order for x to be an eigenvalue of A and AT, there must exist nonzero x and v such thatandUse matrix algebra and the equations from the first step to write matrix equations involving A-AI and AT-XI.The equations areandMatrix AT-X ismatrix A-21.How can this relationship between AT-1 and A-I be used to determine information about X?A. Since the two matrices are equal, the nonzero vector x must be a constant multiple of the nonzero vector v.B. Since the two matrices are transposes, if either (AT-AI)x=0 or (A-AI)v=0 has at least one nontrivial solution, then all of the statements of the Invertible Matrix Theorem are false for both matrices.C. Since the two matrices are inverses, if either (AT-x=0 or (A-AI)v=0 has at least one nontrivial solution, then all of the statements of the Invertible Matrix Theorem are true for both matrices.
Answers
This relationship between AT-1 and A-I be used to determine information about matrix X by option (A) and (C).
(A) Since the two matrices are equal, the nonzero vector x must be a constant multiple of the nonzero vector v and (C) Since the two matrices are inverses, if either (AT-x=0 or (A-AI)v=0 has at least one nontrivial solution, then all of the statements of the Invertible Matrix Theorem are true for both matrices.
Therefore, if A is an eigenvalue of A, then λ must be an eigenvalue of AT, and vice versa. This can be seen by comparing the equation (A-λI)x=0 with the equation (AT-λI)v=0. If x is an eigenvector of A with eigenvalue λ, then it follows that v=x is an eigenvector of AT with eigenvalue λ. And if v is an eigenvector of AT with eigenvalue λ, then it follows that x=v is an eigenvector of A with eigenvalue λ.
To learn more about matrix here:
https://brainly.com/question/11367104
#SPJ4
Evaluate the expression w2 - v+ 1 for W = -2 and v = -8.
A. -11
B. 5
C. 13
D. -3

Answers
Answer:
13
Step-by-step explanation:
w^2 = -2^2 = 4
-v = -1*-8 = 8
Put it together: w^2-v+1 --> 4+8+1 = 13
twelve new students are standing in a line. how many different ways can the first seven students in line order themselves? provide your answer below:
Answers
I hope this can help you out some

Which data set has the greatest sample standard deviation? A. Data set (ii), because it has two entries that are far from the mean. B. Data set (i), because it has more entries that are close to the mean. C. Data set (iii), because it has more entries that are farther away from the mean.
Answers
Data set (ii) because it has two entries that are far from the mean. the deviations from the mean are smaller,
The sample standard deviation measures the dispersion or spread of data points in a data set. To determine which data set has the greatest sample standard deviation, we need to consider the distribution of values relative to the mean.
In data set (ii), which has two entries that are far from the mean, the presence of these outliers can significantly increase the sample standard deviation. Outliers are data points that deviate significantly from the majority of the data, and their inclusion in a data set can inflate the standard deviation.
This is because the standard deviation calculates the average distance between each data point and the mean, and outliers contribute to larger distances.
Data set (i), on the other hand, having more entries that are close to the mean, suggests a more concentrated or clustered distribution of values.
When data points are closer to the mean, the deviations from the mean are smaller, resulting in a smaller standard deviation compared to a data set with outliers.
Data set (iii), with more entries that are farther away from the mean, may also have a higher sample standard deviation. However, without specific information about the magnitude of these deviations and the overall distribution of values,
we cannot definitively conclude that data set (iii) has the greatest standard deviation. Therefore, based on the information provided, the data set (ii) with two entries that are far from the mean is likely to have the greatest sample standard deviation.
Visit here to learn more about standard deviation:
brainly.com/question/29115611
#SPJ11
identify error GIVEN, bracelets - php200 necklaces php300 sales at least 3600 sells at most 50 pieces of bracelets and necklaces correct the errors
Answers
Triangle OPQ, with vertices O(3,4), P(8,3), and Q(4,8), is drawn inside a rectangle, as
shown below.
What is the area, in square units, of triangle OPQ?

Answers
The area of triangle OPQ is 44 square units.
How to find the area of tringle?
There are different ways to find the area of a triangle, depending on the information given. Here are a few common methods:
Using the base and height: To find the area of a triangle using the base and height, you can use the formula: A = (1/2)bhwhere A is the area, b is the base and h is the height.The height is the perpendicular line segment drawn from the vertex of the triangle to the line containing the base of the triangle.Using the 3 sides of the triangle: Heron's formula is a method to find the area of a triangle when the lengths of all three sides are known. The formula is:A = √(s(s-a)(s-b)(s-c))where A is the area, a, b and c are the sides of the triangle, and s is the semi-perimeter of the triangle.s = (a+b+c)/2There are different methods to find the area of a triangle, but one common method is to use the coordinates of its vertices and the distance formula. The distance formula is
d = √((x2-x1)^2 + (y2-y1)^2)
We can use the distance formula to find the lengths of the sides of the triangle OPQ, which are:
OP = √((8-3)^2 + (3-4)^2) = √((5)^2 + (-1)^2) = √(25+1) = √26
OQ = √((4-3)^2 + (8-4)^2) = √((1)^2 + (4)^2) = √(1+16) = √17
PQ = √((4-8)^2 + (8-3)^2) = √((-4)^2 + (5)^2) = √(16+25) = √41
Once we have the lengths of the sides of the triangle, we can use the Heron's formula to find its area:
s = (OP + OQ + PQ)/2
Area = √(s(s-OP)(s-OQ)(s-PQ))
s = (√26 + √17 + √41)/2 = (√44)/2 = 4√11
Area = √(4√11(4√11-√26)(4√11-√17)(4√11-√41))
Area = √(4√11 * √(44-26) * √(44-17) * √(44-41))
Area = √(4√11 * √18 * √27 * √3)
Area = √(4√11 * 3√2 * 3√3 * √3)
Area = 4*11 = 44 square units
Hence, the area of triangle OPQ is 44 square units.
To learn more about Area of triangle, Visit
https://brainly.com/question/17335144
#SPJ1
Ak190 has the best answers
Answers
Answer:
bhi
Step-by-step explanation:
hf
Answer:
ok
Step-by-step explanation:
Find the rate of change of y with respect to x if dy dx x²y-5+2 ln y = x³
Answers
The rate of change of y with respect to x is given by dy/dx = xy - (3/2)x²y.
To find the rate of change of y with respect to x, we need to differentiate the given equation. The rate of change can be determined by taking the derivative of both sides of the equation with respect to x.
First, let's differentiate each term separately using the rules of differentiation.
Differentiating x²y with respect to x gives us 2xy using the product rule.
To differentiate 5, we know that a constant has a derivative of 0.
Differentiating 2ln(y) with respect to x requires the chain rule. The derivative of ln(y) with respect to y is 1/y, and then we multiply by dy/dx. So, the derivative of 2ln(y) is 2/y * dy/dx.
Differentiating x³ gives us 3x² using the power rule.
Now, we can rewrite the equation with its derivatives:
2xy - 2/y * dy/dx = 3x²
To solve for dy/dx, we can isolate it on one side of the equation. Rearranging the equation, we get:
2xy = 2/y * dy/dx + 3x²
To isolate dy/dx, we move the term 2/y * dy/dx to the other side:
2xy - 2/y * dy/dx = 3x²
2xy = 2/y * dy/dx + 3x²
2/y * dy/dx = 2xy - 3x²
Now, we can solve for dy/dx by multiplying both sides by y/2:
dy/dx = (2xy - 3x²) * (y/2)
Simplifying further, we have:
dy/dx = xy - (3/2)x²y
To know more about rate of change, refer here:
https://brainly.com/question/29181688#
#SPJ11
please help asap !! (images below)
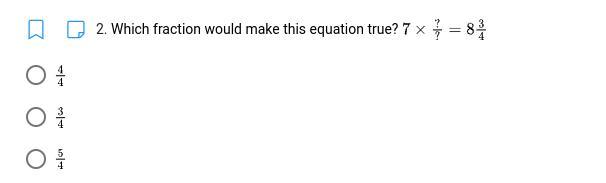

Answers
Answer:
5/4 and then 5/3
Step-by-step explanation:
rewrite the expression in the form as a^n

Answers
good luck :)))))
James age is 3 years less than twice Tori's age the sum of their ages is 30 find their ages
Answers
Please solve all the questions!I will thumb you up! Thanks!
1. The following is a list of data management final grades. [K5] 92 48 59 62 66 98 70 70 55 63 70 97 61 53 56 64 46 69 58 64 2. For question #1 determine the following [K6] a) The three measures of ce
Answers
The measures of central tendency for the given data set are:
- Mean: 59.85
- Median: 61.5
- Mode: None
To determine the three measures of central tendency for the given data set, we can calculate the mean, median, and mode.
a) Mean:
The mean, also known as the average, is calculated by summing up all the values in the data set and dividing it by the total number of values. In this case, we add up all the final grades and divide by the total number of grades:
92 + 48 + 59 + 62 + 66 + 98 + 70 + 70 + 55 + 63 + 70 + 97 + 61 + 53 + 56 + 64 + 46 + 69 + 58 + 64 = 1197
The total number of grades is 20.
Mean = 1197 / 20 = 59.85
Therefore, the mean of the final grades is approximately 59.85.
b) Median:
The median is the middle value in a sorted list of data. To find the median, we first need to sort the grades in ascending order:
2, 46, 48, 53, 55, 56, 58, 59, 61, 62, 63, 64, 64, 66, 69, 70, 70, 92, 97, 98
Since the total number of grades is even (20), we take the average of the two middle values:
Median = (61 + 62) / 2 = 61.5
Therefore, the median of the final grades is 61.5.
c) Mode:
The mode is the value that appears most frequently in the data set. In this case, there is no value that appears more than once. Therefore, there is no mode for the final grades.
For more such questions on central tendency
https://brainly.com/question/28180169
#SPJ8
Guysss I need to know the question
If you skip count by 4’s starting with 8, what will the 11 number be?
I need to know lang naman kase assignment ko ehh chaar nasa math book ko Baka kase pag arlan namin kaya ko tinatanong
Answers
Answer:
88 i think so
Step-by-step explanation:
J(13,-5), K(2, 6), L(-1,-5), M(-4,-2)
J10
L(-3,2
Answers
Answer:
is there a graph for this
Step-by-step explanation:
i need a grapg or to know what they wanted to know
The cost of a trip is $3.15 plus $0.95 for every kilometre that you ride on a bus. Which of the following expressions gives the cost of a trip of k kilometres?
Answers
Answer: 0.95k + 3.15
Step-by-step explanation:
0.95k is because each of k kilometers costs $0.95. + 3.15 is because it costs 3.15 as a flat rate regardless of distance
Hope it helps <3
Answer:
.95k+3.15
Step-by-step explanation:
To write an expression you need a variable (k). I look at the directions and I see that the length of the trip is 'k' kilometers. So I pay the flat fee of 3.15 ONE TIME. Then I pay $0.95 for every kilometer I go, so the expression is
-> .95k+3.15