A 28-year-old earns an average income and plans to retire in 37 years. The employee plans to begin making $5,500 annual contributions into an
IRA.
Which type of IRA is best for the employee, and why?
O The Traditional IRA is the best choice because the employee will pay less in taxes during employment than in retirement.
The Traditional IRA is the best choice because the employee will pay more in taxes during employment than in retirement.
O The Roth IRA is the best choice because the employee will pay more in taxes during employment than in retirement.
O The Roth IRA is the best choice because the employee will pay less in taxes during employment than in retirement.

Answer:

the perimeter is 960

Step-by-step explanation:

The computation of the perimeter is shown below;

If we assume

= (24 × 2) + (6 × 2)

= 48 + 12

= 60

And, the area is 16 times to that of original So

= 60 × 16

Hence, the perimeter is 960

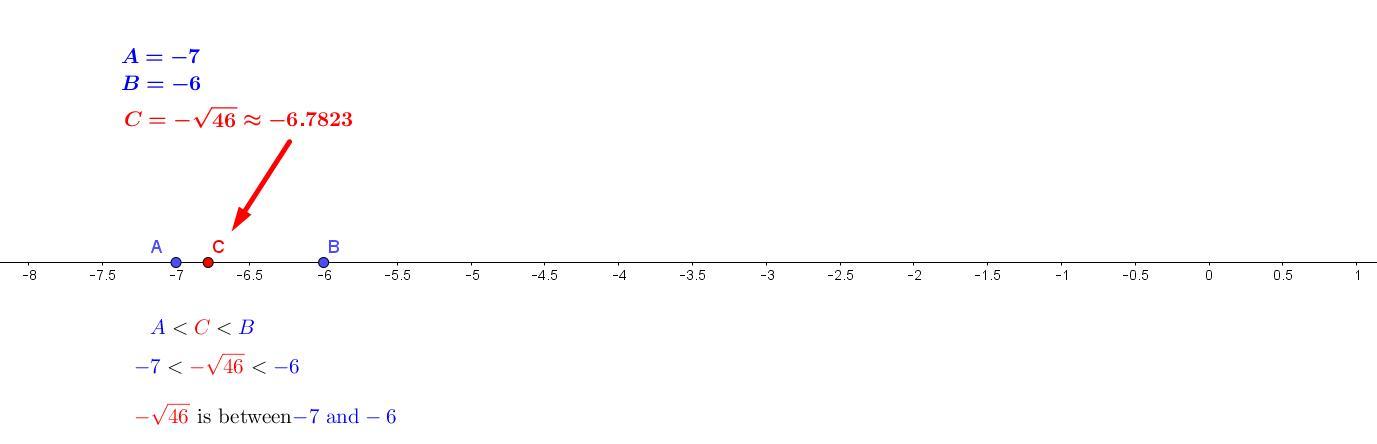
Answer:

Step-by-step explanation:

so if this = that then this = x plus five 5 into 9

is

6 9 420 = 69x so pls go away 4848]

568393=334-0i34-0 o

Answer:

It is 40.

Step-by-step explanation:

This is because the rectangle is 24, and both the triangles are 8.

The absolute maximum value of the function f(t) is 2 and the absolute minimum value of the function f(t) is -10 at t = -1 and t = 5 respectively.

Given function: The given capability can be communicated as: f(t) = t  3t, [1, 5]. f(t) = t (1 - 3) = - 2tWe must determine the given capability's greatest and absolute smallest benefits. To determine the maximum and minimum values of the given function, the following steps must be taken: Step 1: Step 2: Within the allotted time, identify the function's critical numbers or points. Step 3: At the critical numbers and the ends of the interval, evaluate the function. To decide the capability's outright most extreme and outright least qualities inside the given interval1, analyze these numbers. Assuming we partition f(t) by t, we get f′(t) = - 2.

The basic focuses are those places where the subsidiary is either unclear or equivalent to nothing. Because the subordinate is characterized throughout the situation, there are no fundamental focuses within the allotted time.2. How about we find the worth of the capability toward the finish of the span, which is f(- 1) and f(5): f(-1) = -2(-1) = 2f(5) = -2(5) = -10. This implies that irrefutably the greatest worth of the capability f(t) is 2 and unquestionably the base worth of the capability f(t) is - 10 at t = - 1 and t = 5, individually. " The response that is required is "The absolute maximum value of the function f(t) is 2 and the absolute minimum value of the function f(t) is -10 at t = -1 and t = 5 respectively."

To know more about function refer to

https://brainly.com/question/30721594

#SPJ11

Answer:

30/3 = 10

he can 10 pieces

Step-by-step explanation:

To find the equation of the line passing through (3, 5) and parallel to the line containing (-4, 0) and (-1, -2), we need to use the slope-intercept form of a line:

y = mx + b

where m is the slope of the line and b is the y-intercept.

First, we need to find the slope of the line containing (-4, 0) and (-1, -2):

m = (y2 - y1) / (x2 - x1)

m = (-2 - 0) / (-1 - (-4))

m = -2 / 3

Since the line we're looking for is parallel to this line, it will have the same slope.

Now we can use the point-slope form of a line to find the equation of the line passing through (3, 5) with slope -2/3:

y - y1 = m(x - x1)

y - 5 = (-2/3)(x - 3)

Simplifying and rearranging, we get:

y = (-2/3)x + 7

So the equation of the line containing the point (3, 5) and parallel to the line containing (-4, 0) and (-1, -2) is y = (-2/3)x + 7.

I Believe This is the answer

Answer: The line through (-4, -6, 1) and (-2, 0, -3), is parallel to the line through (10, 18, 4) and (5, 3, 14).

Step-by-step explanation:

Have a Great Day

Using the simplex method, the optimal solution for the given linear program is z = 14, with x1 = 0 and x2 = 5. There are no alternative optimal solutions.

To solve the linear program using the simplex method, we start by converting the problem into standard form with all constraints in the form of inequalities and non-negative variables. The initial tableau for the problem is as follows:

 |   x1  |   x2  |   s1   |   s2   |   b   |

--------------------------------------------

z |  -3   |   6   |   0    |   0    |   0   |

--------------------------------------------

s1|   5   |   7   |   1    |   0    |   35  |

--------------------------------------------

s2|  -1   |   2   |   0    |   1    |   2   |

--------------------------------------------

Next, we perform the simplex iterations to improve the objective function value. After performing the necessary row operations, we arrive at the final tableau:

 |   x1  |   x2  |   s1   |   s2   |   b   |

--------------------------------------------

z |   0   |   1   |  3/2   |  -1/2  |   14  |

--------------------------------------------

s1|   0   |   0   |   4    |   3    |   5   |

--------------------------------------------

s2|   1   |   0   |  -1/2  |   5/2  |   3   |

--------------------------------------------

From the final tableau, we can see that the optimal solution is z = 14, with x1 = 0 and x2 = 5. The decision variable x1 is at its lower bound, indicating that it is non-basic. Therefore, there are no alternative optimal solutions in this case.

In summary, the optimal solution for the given linear program is z = 14, with x1 = 0 and x2 = 5. There are no alternative optimal solutions.

Learn more about simplex method here:

brainly.com/question/15801083

#SPJ11

Answer:

The total paint cost is £380. The total tiles cost is £1800. The total cost is £2180.

Step-by-step explanation:

To know the cost, you need to calculate the area of the community hall.

So together, their area is 1200m2.

Together the two walls have an area of 90m2

Together the two big walls have an area of 240m2

Painting:

They are going to paint the walls and the ceiling and each 10L tin covers 25m2 so:

Area of the walls and ceiling = 600m2 + 90m2 + 240m2 = 930m2

930m2 ÷ 25m2 = 37.5 tins. Since you can't have half a tin, they will need 38 10L tins.

38 x £10 = £380

Floor:

1m2 floor tiles costs £3 so 600m2 x £3 = £1800

Total:

£1800 + £380 = £2180

Answer:

C. Adjacent

Step-by-step explanation:

Answer:

1.20$

......................

Answer:

c

Step-by-step explanation:

The red line represents the critical value, and the shaded region on the right-hand side of the red line represents the rejection region. If the calculated test statistic is greater than the critical value of z, which is 1.88 in this case, we will reject the null hypothesis.

The critical value(s) and rejection region(s) for the type of z-test with a level of significance a = 0.03 and a right-tailed test are as follows :Step 1: Determine the critical value of  zThe critical value is calculated by using the normal distribution table and the level of significance. A right-tailed test will have a critical value of zα. For a level of significance of 0.03, we will look for the z-value that corresponds to 0.03 in the normal distribution table.Critical value for a = 0.03 is z = 1.88 (approx).Step 2: Determine the Rejection Region The rejection region for a right-tailed test is defined as any z-value that is greater than the critical value. That is, if the test statistic is greater than 1.88, we reject the null hypothesis at the 0.03 level of significance, and if it is less than or equal to 1.88, we fail to reject the null hypothesis.Therefore, the rejection region for a right-tailed test with a level of significance of 0.03 is as follows:Rejection Region: Z > 1.88  OR  Z ≤ -1.88Graph: The graph for the given values will be as follows:The red line represents the critical value, and the shaded region on the right-hand side of the red line represents the rejection region. If the calculated test statistic is greater than the critical value of z, which is 1.88 in this case, we will reject the null hypothesis.

To know more about  critical value Visit:

https://brainly.com/question/32607910

#SPJ11

Answer: No real solutions

Step-by-step explanation: to solve for x and find a solution you need to take the square root of -144

This is not possible as this a negative number . There is a solution if we use complex numbers, but this not included in the question

The standard deviation is 0.1243, given the variance to be 0.01545, making option B the right choice.

Dispersion is measured by variance. A metric called a "measure of dispersion" is used to assess how variable data are concerning an average value. There are two sorts of data: grouped and ungrouped. Data is referred to as grouped data when it is presented as class intervals. On the other hand, it is referred to as ungrouped data if it comprises just individual data points. For both types of data, the sample and population variances may be calculated.

The variance of the provided data is obtained by taking the square of the standard deviation. The standard deviation is used to determine how widely distributed the data points are about the mean. In other words, the standard deviation is used to determine how observations in a data collection deviate from the mean. While the standard deviation has the same unit as the population or the sample, variance is represented in square units.

In the question, we are asked to find the standard deviation, if the variance is 0.01545.

We know that Variance = (Standard Deviation)².

This gives us:

Standard Deviation = √Variance,

or, Standard Deviation = √0.01545,

or, Standard Deviation = 0.12429802894 ≈ 0.1243.

Thus, the standard deviation is 0.1243, given the variance to be 0.01545, making option B the right choice.

Learn more about Standard deviation and variance at

https://brainly.com/question/475676

#SPJ1

The mean, median, and mode are:

Mean = 10

Median = 8

Mode = 8

To find the mean, median, and mode of the given set of numbers: 5, 8, 18, 1, 14, 6, 8, 13, 8, 19, we can perform the following calculations:

Mean: The mean is calculated by summing up all the numbers and dividing by the total count of numbers.

Mean = (5 + 8 + 18 + 1 + 14 + 6 + 8 + 13 + 8 + 19) / 10

= 100 / 10

= 10

Therefore, the mean is 10.

Median: The median is the middle value when the numbers are arranged in ascending order. If there are an odd number of values, the median is the middle number. If there are an even number of values, the median is the average of the two middle numbers.

Arranging the numbers in ascending order: 1, 5, 6, 8, 8, 8, 13, 14, 18, 19

Since there are 10 numbers, the median is the average of the two middle numbers, which are the 5th and 6th numbers:

Median = (8 + 8) / 2

= 16 / 2

= 8

Therefore, the median is 8.

Mode: The mode is the number(s) that appear(s) most frequently in the set.

In this case, the number 8 appears three times, which is more than any other number.

Therefore, the mode is 8.

To know more about mean, median, and mode refer here:

https://brainly.com/question/30891252#

#SPJ11

==========================================================

Explanation:

List out the perfect squares

and so on. We can see that 46 is between 6^2 = 36 and 7^2 = 49.

We can say 6^2 < 46 < 7^2

Applying the square root to all three sides leads us to 6 < sqrt(46) < 7

Now multiply all three sides by -1. This will flip the inequality signs

We go from

6 < sqrt(46) < 7

to

-6 > -sqrt(46) > -7

It might help to order things from smallest to largest to get this

-7 < -sqrt(46) < -6

This means -sqrt(46) is between -7 and -6 on the number line

See the diagram below.

Answer:

Step-by-step explanation:

First notice that -√46 lies between -√49 and -√36, that is, between

                                                              -7   and  -6.  

Here all three numbers are negative because they lie to the left of zero (0) on the number line.

The domain and the range of the function in this problem are given as follows:

The function is defined for all real values except x = 3, which is the vertical asymptote, and assumes negative values, hence:

The graph of the function is given by the image presented at the end of the answer.

Learn more about domain and range at https://brainly.com/question/26098895

#SPJ1

Answer:

I dont know. sorry sorry

Answer:

Arithmetic

Step-by-step explanation:

The differential dy for y = tan(4x + 6) when x = 4 and dx = 0.2 is 3.22, the differential dy for y = 3x² + 5x + 4 when x = 5 and dx = 0.2 is 30.20, and the change in y \(∆y\) for y = \(4√x\) when x = 2 and\(∆x = 0.3 is 0.848\).

To find the differential of a function, we use the derivative, which is defined as the limit of the ratio of the change in y to the change in x as the change in x approaches zero. The differential dy is then given by the product of the derivative and the change in x, or simply dy = f'(x) dx.

For the function y = tan(4x + 6), we can find the derivative as follows: f'(x) = sec²(4x + 6) * 4 = 4 sec²(4x + 6) Substituting x = 4 and dx = 0.2, we get: dy = f'(4) * 0.2 = 4 sec²(22) * 0.2. Rounding to two decimal places, we get dy = 3.22.

For the function y = 3x² + 5x + 4, we can find the derivative as follows: f'(x) = 6x + 5 Substituting x = 5 and dx = 0.2, we get: dy = f'(5) * 0.2 = 6(5) + 5 * 0.2 Rounding to two decimal places, we get dy = 30.20.

For the function y = \(4√x\), we can find the derivative as follows: f'(x) = 2/√x Substituting x = 2 and\(∆x = 0.3\), we get: ∆y = f'(2) *\(∆x = 2/√2 * 0.3 = 0.848\) Rounding to three decimal places, we get \(∆y = 0.848\).

Learn more about differential here:

https://brainly.com/question/31383100

#SPJ4

Answer:

Let x = the cost of a movieLet y = the cost of a gameUsing these variables,

we can set up equations.3x + 5y = 42 eq19x + 7y = 72 eq2

We have here a system of equations, where we have two or more equations with two or more different variables.

We use the elimination method to solve for the variables.

Multiply eq1 by 3. Keep eq2.

9x + 15y = 126 eq1

9x + 7y = 72 eq2

Subtract eq2 from eq1 to eliminate the x terms.

8y = 54y  

= 6.75

This rental cost of one video game is $6.75

Substitute the value of y into eq1 to solve for x.

This will give you the rental cost of one movie.

Step-by-step explanation:

Answer:

The square root of 37 is approximately 6.0827. To determine which two integers it lies between, we can find the integers that are closest to the square root of 37.

The integer that is smaller than 6.0827 is 6, and the integer that is larger than 6.0827 is 7.

Therefore, the square root of 37 is between the integers 6 and 7.

In order to calculate the z-scores for the given Confidence Interval (CI) levels, we need to use the Z-table. It is also known as the standard normal distribution table. Here are the z-scores for the given Confidence Interval levels:1. 68% CI: The confidence interval corresponds to 1 standard deviation on each side of the mean.

Thus, the z-score for the 68% \(CI is ±1.00.2. 85% CI\): The confidence interval corresponds to 1.44 standard deviations on each side of the mean.

We can calculate the z-score using the following formula:\(z = invNorm((1 + 0.85)/2)z = invNorm(0.925)z ≈ ±1.44\)Note that invNorm is the inverse normal cumulative distribution function (CDF) which tells us the z-score given a certain area under the curve.3. 99% CI: The confidence interval corresponds to 2.58 standard deviations on each side of the mean. We can calculate the z-score using the following formula:\(z = invNorm((1 + 0.99)/2)z = invNorm(0.995)z ≈ ±2.58\)

Note that in general, to calculate the z-score for a CI level of (100 - α)% where α is the level of significance, we can use the following formula:\(z = invNorm((1 + α/100)/2)\) Hope this helps!

To know more about distribution visit:

https://brainly.com/question/29664127

#SPJ11

Answer:

It would take 9 years for the population to fall below 10000.

Mr. Green should use mean value. The mean temperature is 77.86 degrees Fahrenheit. The Option C.

Temperature refers to the measure of the warmth or coldness of an object or substance with reference to some standard value.

The table values which can be used to represent the temperature are:

To summarize temperatures for each day,he should use the mean (average) temperature because the mean temperature provides a measure of central tendency while taking into account all the data points in the dataset. Therefore, Option C is correct.

Full question:

Mr. Greene created a data set that represents the daily high temperatures, in degrees Fahrenheit, in his city over a week.

The values in the table describe the data set.

Minimum 73

Mean 77.86

Mean Absolute Deviation 2.73

Median 79

InterquartileRange 6

Maximum 82

Mr. Greene wants to use a single number that summarizes the temperatures for each day. Which value should he use? A. interquartile range B. mean absolute deviation C. mean D. maximum.

Read more about measure of centre

brainly.com/question/15214370

#SPJ1

The linear function that gives the boiling point at a given elevation is:

y = -0.00172x + 212.

When the boiling point for water is 190⁰F, the elevation is of 12,791 feet.

A linear function is modeled by:

y = mx + b

In which:

For this problem, we have that:

Hence the linear function that gives the boiling point at a given elevation is:

y = -0.00172x + 212.

When the boiling point for water is 190⁰F, the elevation is found as follows:

190 = -0.00172x + 212.

0.00172x = 22

x = 22/0.00172

x = 12,791 feet.

More can be learned about linear functions at https://brainly.com/question/24808124

#SPJ1

Answer:

6

Step-by-step explanation:

\(a + b + c = 20\)

\(a + b = 14(i)\)

Putting value (a + b) in the above equation

\(14 + c = 20\)

\(c = 20 - 14\)

\(c = 6\)

Answer:

(-4)^5

Step-by-step explanation:

(-4)^(8 + 3)/(-4)^(4 + 2) = (-4)^11/(-4)^(6) = (-4)^(11-6) = (-4)^5

Answer:

Step-by-step explanation:

Given the expression cos(3x-π) = -√3/2, we are to find the values of x that represent the solutions to the equation.

cos(3x-π) = -√3/2

take inverse cos of both sides

cos⁻¹[cos(3x-π)] = cos⁻¹[-√3/2]

3x-π = cos⁻¹[-√3/2]

3x-π = -30°

since 180° = π rad

Hence;

3x- 180° = -30°

3x =  -30°+ 180°

3x = 150°

x = 150°/3

x = 50°

Since cos is negative in the first second and 3rd quadrant;

3x-180° = -30°

In the second quadrant;

3x-180° = 180-30

3x - 180 = 150

3x = 150+180

3x = 330

x = 110°

In the third quadrant;

3x-180° = 270+30

3x - 180 = 300

3x = 300+180

3x = 480

x = 480/3

x = 160