A 18oz pepsi for 2.00 or a 25 oz for 2.30
Answers
Answer: 25 oz for 2.30
Step-by-step explanation:
18oz Pepsi for $2.00
Take 2 divided by 18 = $0.11
25 oz for $2.30
Take 2.3 divided by 25 = $0.09
So 25 oz for 2.30 is better!
Related Questions
PLEASE HELP I WILL GIVE BRAINLIEST my

Answers
Answer:
I think B
Step-by-step explanation:
Answer:
C
Step-by-step explanation:
If you follow rise/run
The rise over run is positive 2/3
i need help please what is x > -8 look like on a number line
Answers
Because x is greater than -8, the arrow is pointing to the left,
Because it is greater than, not greater than/equal to, the dot is empty.
Sorry if its a bit messy, I don't have amazing drawing skills on the computer. It should give a general idea though.

y=1x+2 y=3x-4 use substtiution
Answers
Answer:
3Y - 4X - 4
Step-by-step explanation:

Lennyn buys a 15-pound bag of potatoes for $3.71. To the nearest cent, how much is 1 pound of potatoes?
Answers
Answer:
3.71/15= 0.24733
1 lbs of potatoes= 0.25 cents
Using the standard normal distribution, find each probability.
P(0 < z < 2.16)
P(−1.87 < z < 0)
P(−1.63 < z < 2.17)
P(1.72 < z < 1.98)
P(−2.17 < z < 0.71)
P(z > 1.77)
P(z < −2.37)
P(z > −1.73)
P(z < 2.03)
P(z > −1.02)
Answers
The probability of each is 0.4832, 0.4686, 0.8474, 0.0808, 0.6656, 0.0384, 0.0083, 0.9582, 0.9798, and 0.8461 respectively.
The z-score represents the number of standard deviations a value is from the mean in a standard normal distribution. By referencing the z-score table, we can determine the probabilities associated with specific z-score intervals.
To find the probabilities using the standard normal distribution, we can utilize a standard normal distribution table or a statistical software.
The standard normal distribution table provides the cumulative probability up to a given value of z, denoted as Φ(z).
Using the standard normal distribution table or a statistical software, we can find the probabilities for the given intervals:
1. P(0 < z < 2.16) = 0.4832
2. P(-1.87 < z < 0) = 0.4686
3. P(-1.63 < z < 2.17) = 0.8474
4. P(1.72 < z < 1.98) = 0.0808
5. P(-2.17 < z < 0.71) = 0.6656
6. P(z > 1.77) = 0.0384
7. P(z < -2.37) = 0.0083
8. P(z > -1.73) = 0.9582
9. P(z < 2.03) = 0.9798
10. P(z > -1.02) = 0.8461
Therefore, the probabilities are as follows:
- P(0 < z < 2.16) = 0.4832
- P(-1.87 < z < 0) = 0.4686
- P(-1.63 < z < 2.17) = 0.8474
- P(1.72 < z < 1.98) = 0.0808
- P(-2.17 < z < 0.71) = 0.6656
- P(z > 1.77) = 0.0384
- P(z < -2.37) = 0.0083
- P(z > -1.73) = 0.9582
- P(z < 2.03) = 0.9798
- P(z > -1.02) = 0.8461
To know more about cumulative probability refer here:
https://brainly.com/question/30825334#
#SPJ11
Sam's Cat Hotel operates 52 weeks per year, 5 days per week, and uses a continuous review inventory system. It purchases kitty litter for $10.75 per bag. The following information is available about these bags. Refer to the standard normal table for z-values. > Demand = 100 bags/week > Order cost = $57/order > Annual holding cost = 30 percent of cost > Desired cycle-service level = 92 percent Lead time = 1 week(s) (5 working days) Standard deviation of weekly demand = 16 bags Current on-hand inventory is 310 bags, with no open orders or backorders.a. What is the EOQ? What would the average time between orders (in weeks)?
b. What should R be?
c. An inventory withdraw of 10 bags was just made. Is it time to reorder?
D. The store currently uses a lot size of 500 bags (i.e., Q=500). What is the annual holding cost of this policy? Annual ordering cost? Without calculating the EOQ, how can you conclude lot size is too large?
e. What would be the annual cost saved by shifting from the 500-bag lot size to the EOQ?
Answers
The required answer is the annual cost saved by shifting from the 500-bag lot size to the EOQ is $1,059.92.
Explanation:-
a. Economic order quantity (EOQ) is defined as the optimal quantity of inventory to be ordered each time to reduce the total annual inventory costs.
It is calculated as follows: EOQ = sqrt(2DS/H)
Where, D = Annual demand = 100 x 52 = 5200S = Order cost = $57 per order H = Annual holding cost = 0.30 x 10.75 = $3.23 per bag per year .Therefore, EOQ = sqrt(2 x 5200 x 57 / 3.23) = 234 bags. The average time between orders (TBO) can be calculated using the formula: TBO = EOQ / D = 234 / 100 = 2.34 weeks ≈ 2 weeks (rounded to nearest whole number).
Hence, the EOQ is 234 bags and the average time between orders is 2 weeks (approx).b. R is the reorder point, which is the inventory level at which an order should be placed to avoid a stockout.
It can be calculated using the formula:R = dL + zσL
Where,d = Demand per day = 100 / 5 = 20L = Lead time = 1 week (5 working days) = 5 day
z = z-value for 92% cycle-service level = 1.75 (from standard normal table)σL = Standard deviation of lead time demand = σ / sqrt(L) = 16 / sqrt(5) = 7.14 (approx)
Therefore,R = 20 x 5 + 1.75 x 7.14 = 119.2 ≈ 120 bags
Hence, the reorder point R should be 120 bags.c. An inventory withdraw of 10 bags was just made. Is it time to reorder?The current inventory level is 310 bags, which is greater than the reorder point of 120 bags. Since there are no open orders or backorders, it is not time to reorder.d. The store currently uses a lot size of 500 bags (i.e., Q = 500).What is the annual holding cost of this policy.
Annual ordering cost. Without calculating the EOQ, how can you conclude the lot size is too large?Annual ordering cost = (D / Q) x S = (5200 / 500) x 57 = $592.80 per year.
Annual holding cost = Q / 2 x H = 500 / 2 x 0.30 x 10.75 = $806.25 per year. Total annual inventory cost = Annual ordering cost + Annual holding cost= $592.80 + $806.25 = $1,399.05Without calculating the EOQ, we can conclude that the lot size is too large if the annual holding cost exceeds the annual ordering cost.
In this case, the annual holding cost of $806.25 is greater than the annual ordering cost of $592.80, indicating that the lot size of 500 bags is too large.e.
The annual cost saved by shifting from the 500-bag lot size to the EOQ can be calculated as follows:Total cost at Q = 500 bags = $1,399.05Total cost at Q = EOQ = Annual ordering cost + Annual holding cost= (D / EOQ) x S + EOQ / 2 x H= (5200 / 234) x 57 + 234 / 2 x 0.30 x 10.75= $245.45 + $93.68= $339.13
Annual cost saved = Total cost at Q = 500 bags - Total cost at Q = EOQ= $1,399.05 - $339.13= $1,059.92
Hence, the annual cost saved by shifting from the 500-bag lot size to the EOQ is $1,059.92.
To know about annual cost . To click the link.
https://brainly.com/question/14784575.
#SPJ11
what is the probability of picking three aces from a standard deck of cards when you pick three cards without replacement? there are 52 cards in a standard deck of cards; there are four aces in the deck.
Answers
The probability of picking three aces from a standard deck of cards when you pick three cards without replacement is approximately 0.0060 or 0.60%.
In a standard deck of 52 cards, there are four aces. When you pick the first card, the probability of selecting an ace is 4/52 since there are four aces out of 52 cards. After the first ace is picked, there are 51 cards left in the deck, including three aces. Therefore, the probability of selecting a second ace, without replacement, is 3/51. Finally, after two aces have been selected, there are 50 cards remaining in the deck, including two aces. The probability of selecting the third ace, without replacement, is 2/50. To calculate the overall probability of picking three aces, we multiply the probabilities of each event together: (4/52) * (3/51) * (2/50) ≈ 0.0060. Thus, there is approximately a 0.60% chance of picking three aces from a standard deck of cards when selecting three cards without replacement.
Learn more about probability here:
https://brainly.com/question/23417919
#SPJ11
7. for 100/300 bodily injury limits and $100,000 property damage limits,
stephanie ambrose's base premium is $292.50. her base premium is
$75.90 for $50-deductible comprehensive insurance and $225.79 $50-
deductible collision insurance. what is ambrose's annual base premium?
(section 9-4) *
a. $595.00
b. $594.19
c. $658.60
d. $495.91
Answers
Stephanie Ambrose's annual base premium is $594.19. b.
To calculate Stephanie Ambrose's annual base premium, we need to add her base premium for bodily injury and property damage limits to the premiums for comprehensive and collision insurance.
Given:
Base premium for bodily injury and property damage limits:
$292.50
Premium for $50-deductible comprehensive insurance: $75.90
Premium for $50-deductible collision insurance: $225.79
To calculate the annual base premium, we sum up all these values:
Annual Base Premium = Base Premium + Comprehensive Premium + Collision Premium
Annual Base Premium = $292.50 + $75.90 + $225.79
Calculating this sum gives us:
Annual Base Premium = $594.19
For similar questions on annual base premium
https://brainly.com/question/21164644
#SPJ8
5x+3=4x. solve for x
Answers
As per given by the question,
There are given given that the equation,
The equation is,
\(5x+3=4x\)Now,
For finding the value of x,
The given equation can be written as;
\(5x+3-4x=0\)Now,
\(\begin{gathered} 5x+3-4x=0 \\ x+3=0 \\ x=-3 \end{gathered}\)Hence, the value of x is -3.
The perimeter of a triangle is 44 inches. The length of one side is twice the length of the shortest side, and the length of the other side is eight inches longer than the length of the shortest side.
Choose a variable and tell what that variable represents.
Answers
Answer:
side a = Smallest = 9 inches
side b = 18 inches
side c = 17 inches
Step-by-step explanation:
The formula for the perimeter of a triangle = side a + side b + side c
side a = Smallest
The perimeter of a triangle is 44 inches.
The length of one side is twice the length of the shortest side
Hence:
b = 2a
The length of the other side is eight inches longer than the length of the shortest side.
Hence,
c = 8 + a
Hence, we substitute into the Intial formula
a + 2a + 8 + a = 44 inches
4a + 8 = 44
4a = 44 - 8
4a = 36
a = 36/4
a = 9 inches
Solving for b
b = 2a
b = 2 × 9 inches = 18 inches
Solving for c
c = a + 8
c = 9 inches + 8 = 17 inches
NEED HELP ASAP…..plz help

Answers
The answer is B) y = 4x
Explanation: If you substitute each number in the x column for the variable x, and then multiple that number by 4, you'll get the number in the y column to the right.
For example:
y = 4x --> y = 4 (2) --> y = 8
I hope this helped. :)
find the range of the function f(x)=2x+4
Answers
Answer:
(0,4)
Step-by-step explanation:
this is highest and only Y intercept. the range of a graph is all of the Y intercepts. and the domain of a graph is all of the x-intercepts

really need help pls

Answers
Answer:
∠1 = 45°
∠2 = 45°
∠3 = 45°
∠4 = 90°
BC = 12
AB = 12
DC = 12
EB = 8.5
DB = 17
EC = 8.5
x to the power of 3 plus x to the power of 2 plus x
Answers
Answer:
x(x²+x+1)
Step-by-step explanation:
im not surewhat answer u want but take note this is FACTORIZATION
I-Ready help...... AND DON"T SAY USE A CALCULATOR IT SO EZZ I Would if i flip In COULD DU>>>>>A>>>>>S>>>>S>>>>>'S SORRY TO BE mean XD

Answers
Answer:
-0.099
Step-by-step explanation:
0.9 × -0.11 = -0.099
Your pfp is giving me a seizure
You're like 12
And your cringy
""Sorry to be mean XD""
Determine whether the following sets are equal {3,5, 1) and (1, 3, 5) True False
Answers
The statement "The sets {3, 5, 1} and (1, 3, 5) are equal" is False. The sets differ in their order of elements, and therefore, they are not considered equal based on the mathematical concept of sets.
The two sets in question are {3, 5, 1} and (1, 3, 5). To determine if these sets are equal, we need to consider the elements they contain and the order in which those elements are listed.
In set notation, the order of elements does not matter, and duplicates are ignored. However, in the first set {3, 5, 1}, the order of elements is specified, and there are no duplicates present. On the other hand, the second set (1, 3, 5) is written using parentheses, indicating that the order of elements is significant.
Therefore, the sets {3, 5, 1} and (1, 3, 5) are not equal because they differ in the order of elements. The first set lists the elements in the order 3, 5, 1, while the second set lists the elements in the order 1, 3, 5.
To illustrate this, let's consider an example of set equality. If we have the sets {1, 2, 3} and {3, 2, 1}, they would be considered equal because the order of elements does not matter in set notation.
For more such questions on sets
https://brainly.com/question/13458417
#SPJ11
If (8z − 9)(8z + 9) = az2 − b, what is the value of a?
Answers
Explanation:
We use the difference of squares rule to say
(m-n)(m+n) = m^2 - n^2
So in this particular case,
(8z-9)(8z+9) = (8z)^2-(9)^2 = 64z^2 - 81
We can see that the 64 matches with the 'a' of the expression az^2-81, which must mean a = 64
Side note: This means b = 81
Answer:
64
Step-by-step explanation:
took the test
Graphs
Information given: Y=4/5x+(-3)
Slope: m= 4/5
Y-intercept= -3
What I need to know :
Write the equation of the line that will intersect at a 90 degree
Answers
Answer:
\(\displaystyle y=-\frac{5}{4}x-3\)
Step-by-step explanation:
Recall that perpendicular lines form a 90-degree angle, so the slope of the line perpendicular to the given equation will be the opposite reciprocal.
Hence, the equation of the line that will intersect at a 90-degree angle is \(\displaystyle y=-\frac{5}{4}x-3\)
A snail is moving at a rate of three inches every two minutes. How fast is the snail moving in feet per hour?
Answers
Pls mark brainliest

Step-by-step explanation:
Their are 60 minutes in a hour, and 12 inches make a foot
the snail is moving 3 inches every 2 minutes , in a hour the snail will move 20 inches
(please give brainliest
What weight would give a newborn a z-score of −0. 75? grams.
Answers
The weight would give a newborn a z-score of −0. 75 with mean 3500 g and standard deviation 500 g is 3125 grams.
What is the normally distributed data?Normally distributed data is the distribution of probability which is symmetric about the mean.
The mean of the data is the average value of the given data. The standard deviation of the data is the half of the difference of the highest value and mean of the data set.
A newborn who weighs 2,500 g or less has a low birth weight. use the information on he right to find the z score of a 2,500 g baby.
From the given parameters, the mean of the data is,
\(\mu=3500\)
The standard deviation of the data is,
\(\sigma=500\)
Thus, the z score can be given as,
\(z=\dfrac{x-\mu}{\sigma}\\-0.75=\dfrac{x-3500}{500}\\x=3125\)
Hence, the weight would give a newborn a z-score of −0.75 with mean 3500 g and standard deviation 500 g is 3125 grams.
Learn more about the normally distributed data here;
https://brainly.com/question/6587992
Learn more about the z score here;
https://brainly.com/question/13299273
what is inverse of matrix
Answers
Answer:
linear algebra, an n-by-n square matrix A is called invertible, if there exists an n-by-n square matrix B such that \mathbf {AB} =\mathbf {BA} =\mathbf {I} _{n}\ where Iₙ denotes the n-by-n identity matrix and the multiplication used is ordinary matrix multiplication.
Answer:
Brainliest pls
Step-by-step explanation:
The inverse of a square matrix A, denoted by A-1, is the matrix so that the product of A and A-1 is the Identity matrix.
in hyperbolic geometry, if three points are not collinear, there is always a circle that passes through them.
T/F
Answers
The statement, in hyperbolic geometry, if three points are not collinear, there is always a circle that passes through them is false.
What is circle?
A circle is a basic geometric shape in mathematics that is defined as a set of points in a plane that are equidistant from a fixed point called the center. The distance between any point on the circle and the center is known as the radius of the circle.
False.
In hyperbolic geometry, if three points are not collinear, there is not always a circle that passes through them. This is in contrast to Euclidean geometry, where three non-collinear points always determine a unique circle.
In hyperbolic geometry, the concept of a circle is different, and the properties of circles are different as well. In fact, in hyperbolic geometry, circles can have infinitely many distinct properties, and not every set of three non-collinear points can be part of a circle.
Therefore, the statement, in hyperbolic geometry, if three points are not collinear, there is always a circle that passes through them is false.
To learn more about circle visit:
https://brainly.com/question/24375372
#SPJ4
x 1 2 3 4
f(X) 0.2 0.5 0.2 0.1
This problem requires R: follow the instruction on the class webpage to install Rstudio. Using the data of Problem (1), use R to do the following. (a) Plot the probability mass function. Remember to label the x and y axes. (b) Verify that the values of the probability add up to 1. (c) Plot the cumulative distribution function. Remember to label the x and y axes.
Answers
The sum of probabilities is equal to 1, so the probabilities are correctly normalized.
To perform the tasks using R, first, make sure you have R and RStudio installed on your computer. Then, follow these steps:
Step 1: Enter the data into R.
# Enter the data
x <- c(1, 2, 3, 4)
f_x <- c(0.2, 0.5, 0.2, 0.1)
Step 2: Plot the probability mass function (PMF).
# Plot the probability mass function
plot(x, f_x, type = "h", lwd = 10, col = "blue", xlab = "X", ylab = "P(X)", main = "Probability Mass Function")
Step 3: Verify that the probabilities add up to 1.
# Verify that the probabilities add up to 1
sum_probabilities <- sum(f_x)
print(paste("Sum of probabilities: ", sum_probabilities))
Step 4: Calculate the cumulative distribution function (CDF) and plot it.
# Calculate the cumulative distribution function
cdf <- cumsum(f_x)
# Plot the cumulative distribution function
plot(x, cdf, type = "s", lwd = 3, col = "red", xlab = "X", ylab = "F(X)", main = "Cumulative Distribution Function")
Sum of probabilities = 0.2 + 0.5 + 0.2 + 0.1 = 1
The sum of probabilities is equal to 1, so the probabilities are correctly normalized.
Make sure to execute each step in the RStudio console or script. The plots will appear in separate windows, and the sum of probabilities will be displayed in the console. The PMF plot will show vertical lines with heights corresponding to the probabilities, and the CDF plot will show a step function.
Learn more about probability mass function here
https://brainly.com/question/30765833
#SPJ4


What's the answer to this question?

Answers
Answer:
yaaaaaaaaaaaaaaaaaaaaa
Step-by-step explanation:
sssssssssssszsssssss
Step-by-step explanation: The domain is the set of all the x terms.
In the graph shown here, we can see that the x terms are increasing
in both a positive and negative direction and there seems to be no
limit to how large or how small the x terms can get.
So the x terms can be all positive or negative numbers,
including decimals and fractions, so our domain is all x-values.
For the range however, we are dealing with the y terms.
Notice that all the y terms are greater than or equal to 0.
So the range is {y: y > or equal to -4}.
So the 1st box and the 5th box should be checked.
Find k'(x) if k(x) = \(e(-\frac{3}{5}x^{-3/5}+2x^{-3/4})\)
![Find k'(x) if k(x) = [tex]e(-\frac{3}{5}x^{-3/5}+2x^{-3/4})[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/vU9g4f5etBfoZnIG7Q5qTF1EUUvfNrSu.png)
Answers
The derivative of k(x) is:
\(k'(x) = e^{ (-3/5*x^{-3/5} + 2*x^{-3/4})}*( (9/25)*x^{-8/5} + (-3/2)*x^{-7/4}})\)
How to find the derivate?Remember the chain rule, if:
h(x) = f( g(x)), then:
h'(x) = f'( g(x))*g'(x)
Here we have the function:
\(k(x) = e^{ (-3/5*x^{-3/5} + 2*x^{-3/4})}\)
The derivate of the exponential is itself, then we will get:
\(k'(x) = e^{ (-3/5*x^{-3/5} + 2*x^{-3/4})}*( (-3/5)*(-3/5)*x^{-3/5 - 1} + 2*(-3/4)*x^{-3/4 - 1}})\\\\k'(x) = e^{ (-3/5*x^{-3/5} + 2*x^{-3/4})}*( (9/25)*x^{-8/5} + (-3/2)*x^{-7/4}})\)
That is the derivate of k(x).
Learn more about the chain rule:
https://brainly.com/question/12047216
#SPJ1
Anybody wanna help me on this?
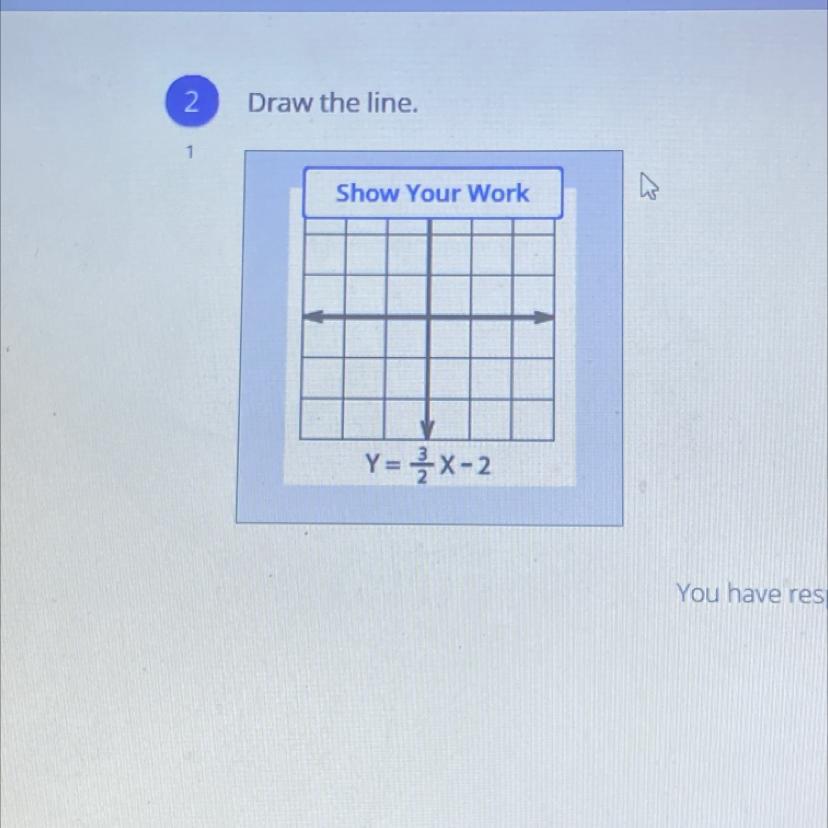
Answers
Answer:
(0,-2) , (2,1) , (4,4)
Step-by-step explanation:
those are the points, now connect then with a line
The following table shows the breakdown of opinions for both faculty and students in a recent survey about the new restructuring of the campus to include an Honors College . Find the probability that a randomly selected person is either a student opposed to the change or a faculty member who has an opinion either for or againstExpress your answer as a fraction in lowest terms or a decimal rounded to the nearest millionth

Answers
Answer:
\(0.416667\)Explanation:
Here, we want to calculate the probability that a randomly selected person is either a student opposed to the change or a faculty member who has an opinion either for or against
We need to get these values
The count of students who are opposed is 59
The count of faculty members who have an opinion either for or against is 16 + 10 = 26
This gives a total of 85
Now, we need to divide this by the total number of students which is 204
Mathematically, we have that as:
\(\frac{85}{204}\text{ = 0.416667}\)
Anita plans to cover a solid cone with construction paper for a science project. The cone has a diameter of 11 inches and a slant height of 28.5 inches. How many square inches of paper will she need to cover the entire cone? (Use 3.14 for Pi and round to the nearest hundredth. Recall the formula S A = pi r l + pi r squared.) 492.20 in.2 587.18 in.2 982.82 in.2 984..39 in.2
Answers
Answer:
587.18 in²
Step-by-step explanation:
In the above question, we are given the following values
Diameter = 11 inches
Radius = Diameter/2 = 11 inches/2 = 5.5 inches
Slant height = 28.5 inches.
We were asked to find how many square inches of paper will she need to cover the ENTIRE cone.
To solve for this, we would use formula for Total Surface Area of a Cone
Total Surface Area of a Cone = πrl + πr²
= πr(r + l)
Using 3.14 for π
Total Surface Area of a Cone
= 3.14 × 5.5( 5.5 + 28.5)
= 3.14 × 5.5 × (34)
= 587.18 in²
Therefore, Anita will need 587.18 square inches of paper to cover the entire cone.
Answer:
B
Step-by-step explanation: Just trust me bro
determine µx and σx \from the given parameters of the population and sample size.
µ = 84; σ = 18; n = 36
Answers
The mean (µx) and standard deviation (σx) of a sample can be determined using the given parameters of the population mean (µ), population standard deviation (σ), and sample size (n).
In this case, since we are given the population mean (µ = 84), the mean of the sample (µx) will be the same as the population mean.
µx = 84 (same as the population mean)
σx = 18 / √36 = 3 (the population standard deviation divided by the square root of the sample size)
To determine the standard deviation of the sample (σx), we divide the population standard deviation (σ = 18) by the square root of the sample size (n = 36). This is based on the principle that the standard deviation of the sample is expected to be smaller than the standard deviation of the population, and it decreases as the sample size increases.
Therefore, in this scenario, the mean of the sample (µx) is 84, and the standard deviation of the sample (σx) is 3. These values represent the central tendency and variability of the sample data.
Learn more about sample size here:
brainly.com/question/30100088
#SPJ11
21 and 23 can best be described as -
Answers
Answer:
odd numbers
Step-by-step explanation:
you can see that end with odd numbers 1 and three so they can best be described as odd numbers
HOPE YOU FIND IT USEFUL