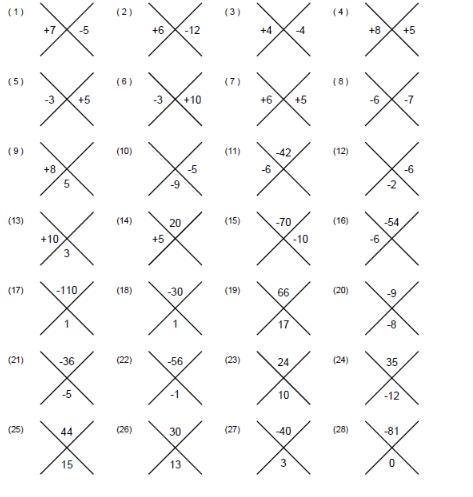
Answers
Answer:
Step-by-step explanation:
1. -35, 2
2. -72, -6
3. -16, 0
4. 40, 13
5. -15, 2
6. -30, 7
7. 30, 11
8. 42, -13
9. -3, -24
10. -4, 20
11. 7, 1
12. 4, -24
13. -7, -70
14. 4, 9
15. 7, -3
16. 9, 3
17. -10, 11
18. 6, -5
19. 11, 6
20. 1, -9
21. -9, 4
22. -8, 7
23. 6, 4
24. -7, -5
25. 11, 4
26. 10, 3
27. -8, 5
28. -9, 0
Related Questions
What does compounded hourly mean
Answers
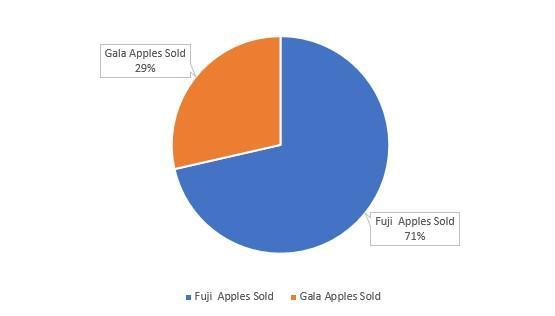
Read the story. Harold runs a farm stand that sells two varieties of apples: Fuji and Gala. Last weekend, he sold 5 pounds of Fuji apples for every 2 pounds of Gala apples he sold. Pick the diagram that models the ratio in the story. If Harold sold 51 more pounds of Fuji apples than of Gala apples, how many pounds of apples did he sell in all? pounds
Answers
Please find the diagram of the pie chart that models the ratio
The sum of the mass of the apples Harold sold in all, based on the ratio of 5 to 2 of the apples sold and the 51 pound more mass of Fuji apples sold is 119 poundsWhat is a ratio?A ratio shows the quantitative relationship between two quantities such that the number of times one quantity is larger than the other is indicated.
The mass of Fuji apples Harold sold for every 2 pound of Gala apples = 5 pounds
First part;
The diagram that models the ratio of the story is given by the a pie chart in which the section is shared in the ratio 5 to 2 as follows;
Sector of the pie chart that represent the mass of the Fuji apples Harold sold = \(\dfrac{5}{5+2} =\dfrac{5}{7}\) of the area of the pie chartThe sector that represent the mass of the Gala apples from the mass of the total apples Harold sold = \(\dfrac{2}{5+2} =\dfrac{2}{7}\) of the area of the pie chartThe pie chart can therefore be constructed using proportional area sizes of \(\dfrac{5}{7}\) and \(\dfrac{2}{7}\)
Second part;
The mass of the Fuji apples Harold sold = 51 pounds + The mass of the Gala apples he soldLet x represent the mass of the Gala apples Harold sold, we can write the following equations;
The mass of the Fuji apples he sold = x + 51
The sum of the mass of the apples Harold sold is therefore; x + x + 51 = 2·x + 51The ratio of the mass of the Fuji apples Harold sold to the total mass of apples he sold is therefore;
\(\dfrac{x + 51}{2\cdot x + 51} =\dfrac{5}{7}\)Which gives; 7·(x + 51) = 5·(2·x + 51)
7·x + 357 = 10·x + 255
10·x - 7·x = 357 - 255 = 102
3·x = 102
\(x = \dfrac{102}{3} =34\)
x = 34
The mass of the Gala apples Harold sold, x = 34 poundsThe mass of the Fuji apples Harold sold = x + 51
Which gives;
x = 34
x + 51 = 34 + 51 = 85
The mass of the Fuji apples Harold sold = 85 poundsThe sum of the mass of apples he sold = 85 pounds + 34 pounds = 119 pounds
Learn more about writing algebraic equations here:
https://brainly.com/question/2972832
#SPJ1
Find the measure of the missing angles.
PLEASEE ANSWER FAST!!!
I've already tried x = 52 and y = 90 but it won't work

Answers
Answer:
x= 52° and y= 142°
Step-by-step explanation:
x combined with angle next to it make a right angle, so you can find x by subtracting 38 from 90. y would be 90 plus 52 because the other angle is the same as x.
Answer:
x = 52° and y = 142°
Step-by-step explanation:
38 + x + the right angle are on straight line.
angles on straight line add up to 180.
so x = 180 - 90 - 38 = 52.
y is the big angle, not the 90.
again, angles on straight line:
y = 180 - 38 = 142
which was EAV-Secure Prove the opposite - i.e. if G is not a PRG, then 3.17 cannot be EAV-secure. Let G be a pseudorandom generator with expansion factor ℓ. Define a private-key encryption scheme for messages of length ℓ as follows: - Gen: on input 1n, choose uniform k∈{0,1}n and output it as the key. - Enc: on input a key k∈{0,1}n and a message m∈{0,1}ℓ(n), output the ciphertext c:=G(k)⊕m. - Dec: on input a key k∈{0,1}n and a ciphertext c∈{0,1}ℓ(n), output the message m:=G(k)⊕c. A private-key encryption scheme based on any pseudorandom generator. THEOREM 3.18 If G is a pseudorandom generator, then Construction 3.17 is a fixed-length private-key encryption scheme that has indistinguishable encryptions in the presence of an eavesdropper. PROOF Let Π denote Construction 3.17. We show that Π satisfies Definition 3.8. Namely, we show that for any probabilistic polynomial-time adversary A there is a negligible function negl such that Pr[PrivKA,Πeav(n)=1]≤21+neg∣(n)
Answers
To prove the opposite, we need to show that if G is not a pseudorandom generator (PRG), then Construction 3.17 cannot be EAV-secure.
Assume that G is not a PRG, which means it fails to expand the seed sufficiently. Let's suppose that G is computationally indistinguishable from a truly random function on its domain, but it does not meet the requirements of a PRG.
Now, consider the private-key encryption scheme Π described in Construction 3.17 using G as the pseudorandom generator. If G is not a PRG, it means that its output is not sufficiently pseudorandom and can potentially be distinguished from a random string.
Given this scenario, an adversary A could exploit the distinguishability of G's output and devise an attack to break the security of the encryption scheme Π. The adversary could potentially gain information about the plaintext by analyzing the ciphertext and the output of G.
Therefore, if G is not a PRG, it implies that Construction 3.17 cannot provide EAV-security, as it would be vulnerable to attacks by distinguishing the output of G from random strings. This contradicts Theorem 3.18, which states that if G is a PRG, then Construction 3.17 achieves indistinguishable encryptions.
Hence, by proving the opposite, we conclude that if G is not a PRG, then Construction 3.17 cannot be EAV-secure.
To know more about pseudorandom generator refer to-
https://brainly.com/question/33563626
#SPJ11
The standard deviation is the blank______ of the variance.
a) square
b) square root
c) inverse exponent
Answers
Standard deviation is the square root of variance .
So,
It is used in measuring any deviation or shift from the calculated mean.
From a data set, the mean of the data can be determined with which the standard deviation can be measure.
Therefore, Standard deviation is use to measure variation that exist in an individual data set. There are different type of data set from which variation is measured.
Learn more on Standard deviation,
brainly.com/question/475676
#SPJ4
Find the height of a cuboid if it's length is 15cm, it's breath is 12cm and it's total surface are is 900cm
Answers
Answer: \(h=8.33\ cm\)
Step-by-step explanation:
Given
The length of a cuboid is \(l=15\ cm\)
breadth is \(b=12\ cm\)
Total surface area is \(S.A.=900\ cm^2\)
Surface area is given by \(2(lb+hl+bh)\)
Insert the values
\(\Rightarrow 900=2(15\times 12+15h+12h)\\\Rightarrow 450=225+27h\\\Rightarrow 225=27h\\\Rightarrow h=8.33\ cm\)
16. A community group is planning the expansion of a square flower garden in a city park. If each side of the original garden is increased by 3 meters, the new total area of the garden will be 225 square meters. Find the length of each side of the original garden. A. 15m B. 3m C. 12m D. Square root of 12m
17. What is the value of c so that x^2-11x+c is a perfect-square trinomial? A. 121, B. 121/4, C. -11/2, D. 121/2
18. PLEASE HELP ASAP! Solve the equation by completing the square. Round to the nearest tenth. X^2+8x=10 A. 1. 1, 9. 1 B. 1. 1,-9. 1 C. -1. 1,9. 1 D. -1. 1, -9. 1
Answers
16. The length of each side of the original garden is 12 meters. The answer is (C) 12m.
17The value of c that makes x^2-11x+c a perfect-square trinomial is (B) 121/4..
18.The answer is (D) -1. 1, -9. 1.
Step by step explanation
16. Let s be the length of each side of the original garden. Then the area of the original garden is s^2. If each side is increased by 3 meters, then the new length of each side is s+3, and the area of the expanded garden is (s+3)^2. We are given that the area of the expanded garden is 225 square meters. Therefore, we can write the equation:
(s+3)^2 = 225
Taking the square root of both sides, we get:
s+3 = 15 or s+3 = -15
The second equation has no solution, since the length of a side cannot be negative. Therefore, we have:
s+3 = 15
Subtracting 3 from both sides, we get:
s = 12
17. To make x^2-11x+c a perfect-square trinomial, we need to add and subtract a constant term to make it a square of a binomial. Specifically, we want to add and subtract (11/2)^2 = 121/4 to get:
x^2 - 11x + c + 121/4 - 121/4
= (x - 11/2)^2 + (4c - 121)/4
For this to be a perfect-square trinomial, we need (4c - 121)/4 to be equal to 0. Therefore, we have:
4c - 121 = 0
Solving for c, we get:
4c = 121
c = 121/4
18. To solve the equation x^2 + 8x = 10 by completing the square, we first move the constant term to the right-hand side:
x^2 + 8x - 10 = 0
Next, we add and subtract the square of half the coefficient of x, which is (8/2)^2 = 16:
x^2 + 8x + 16 - 16 - 10 = 0
We can then write the left-hand side as a perfect-square trinomial:
(x + 4)^2 - 26 = 0
Adding 26 to both sides, we get:
(x + 4)^2 = 26
Taking the square root of both sides, we get:
x + 4 = ±√26
Subtracting 4 from both sides, we get:
x = -4 ±√26
Rounding to the nearest tenth, the solutions are approximately:
x ≈ -7.1 and x ≈ -0.9
To know more about binomial refer to
https://brainly.com/question/29163389
#SPJ11
Can square pieces of foam board, each with an area of 169 square inches, be cut and used to construct a cube with a volume of 1,728 cubic inches? explain.
Answers
No, they cannot construct a cube from the square pieces of foam board.
A square has four equal sides. When we multiply the length and width of a square to determine its area, we are essentially squaring one of its sides because they are the same.
A=s²
If we already know the area, we can work backward and take the square root to find the side:
√169=√s²
13=s
13 inches is the side length.
The length, breadth, and height of a cube are all equal. These three measurements are multiplied to determine a cube's volume; since they are equal, this essentially equals cubing the side length:
V=s³
The volume is 1728, so we have the following:
1728=s³
We take the cubed root and move backwards:
∛1728=∛s³
12=s
So, In order to construct a cube with the given volume 12 should be length of the side but the length of the square is 13 so it is not possible.
To know more about Cube, click here :
https://brainly.com/question/14516390
#SPJ4
ž + 1 = 9
Ox = 16
x = 20
Ox = 4
Ox=5

Answers
Answer:
x = 16
Step-by-step explanation:
x
-- = 9-1 ...... first shift 1 and it will be -1
2
x = 8 ....... secondly 9-1 =8
--
2
x = 16 ..... criss cross and 2×8 = 16
there fore the value of x is equals to 16.
you can check it!
Alex wrote checks on Tuesday for $35 and $40. He also made a deposit in his checking account of $170. Find the overall change in the amount in his checking account.
Answers
Answer: He retrieved 75$ from his account then he put back 170$ so +75 and -170 so in total the answer would be 245$
Answer: He would have $100 in his bank account from the information provided .
Round 91738 to the nearest ten thousand. Enter your answer in the box
below.
Answer here

Answers
Answer:
90,000
Step-by-step explanation:
Based on the graphs of the two functions, which statement is true?

Answers
Answer:f(4)=g(4)
Step-by-step explanation:We see that when x= 4, we see that f(4) intersects g(4)
The locus of point equidistant from three vertices of a triangle is……………
Answers
Answer:
circumcenter
Step-by-step explanation:
You want to know the name of the point equidistant from the vertices of a triangle.
CircumcircleThe circle that passes through the vertices of a triangle is called a "circumcircle". It circumscribes the triangle. Its center is equidistant from all points on the circle, so is equidistant from the triangle's vertices.
The point equidistant from the vertices of a triangle is the circumcenter.
__
Additional comment
The circumcenter is at the intersection of the perpendicular bisectors of the sides of the triangle.
A small business owner contributes $2,000 at the end of each quarter to a retirement account that earns 10% compounded quarterly. (a) How long will it be until the account is worth at least $150,000? (Round your answer UP to the nearest quarter.) 43 quarters (b) Suppose when the account reaches $150,000, the business owner increases the contributions to $4,000 at the end of each quarter. What will the total value of the account be after 15 more years? (Round your answer to the nearest dollar.) $
Answers
After 15 more years of contributions of $4,000 at the end of each quarter, the retirement account will be worth approximately $760,514.47.
To calculate this, we need to use the formula for the future value of a lump sum. A lump sum is a one-time payment made at the beginning or end of a specific period. In this case, we're looking at the future value of the retirement account after 15 more years of contributions.
Using the given information, we can plug in the values and solve for FV:
PV = $150,000
Pmt = $4,000
r = 10%
n = 4 (since interest is compounded quarterly)
t = 15 years
First, we need to calculate the future value of the current investment of $150,000:
FV1 = $150,000 x (1 + 0.1/4)⁴ ˣ ¹⁵ = $548,534.24
Then, we can calculate the future value of the quarterly contributions of $4,000 over 15 years:
FV2 = $4,000 x [(1 + 0.1/4)⁶⁰ - 1] / (0.1/4) = $211,980.23
Finally, we can add FV1 and FV2 to get the total future value of the retirement account after 15 more years:
Total FV = FV1 + FV2 = $548,534.24 + $211,980.23 = $760,514.47
To know more about retirement here
https://brainly.com/question/20751552
#SPJ4
0.510 (3+0.2) x -1.6
-
Answers
Answer:
-2.6112
Step-by-step explanation:
= 0.510 (3+0.2) x -1.6
= 0.510 x 3.2 x -1.6
= -2.6112
hence answer is -2.6112.
find the general solution of the given system of equations. x' = (5 1 -26 -5)x (-cost sint) x = c_1(5cost - sint -cost)
Answers
The system of equations general solution is denoted by the following notation:
\(\[x = c_1 \cdot e^{\sqrt{51}t} \cdot \begin{pmatrix} 1 \\ \sqrt{51} - 5 \end{pmatrix} + c_2 \cdot e^{-\sqrt{51}t} \cdot \begin{pmatrix} 1 \\ -\sqrt{51} - 5 \end{pmatrix}\]\)
where t stands for the independent variable (time) and c_1 and c_2 are arbitrary constants.
What is Linear algebra?
The study of vector spaces and linear transformations is the focus of the mathematical field known as linear algebra. It includes the geometric and algebraic characteristics of matrices and vectors.
Vectors are used in linear algebra to describe quantities that have both a magnitude and a direction. They can be multiplied by one another, scaled using scalars, and put through a variety of procedures. Contrarily, matrices are rectangular arrays of numbers that can be used to represent a variety of mathematical structures, including systems of equations and linear transformations.
Let's begin by reformatting the system of equations into a matrix form in order to get the general solution:
\(\[x' = \begin{pmatrix} 5 & 1 \\ -26 & -5 \end{pmatrix} x\]\)
where x is the (x, y) column vector.
We can determine the eigenvalues and eigenvectors of the coefficient matrix (5 1; -26 -5) to solve this system.
We begin by computing the eigenvalues by resolving the defining equation:
\(\[\det(A - \lambda I) = 0\]\)
where A is the matrix of coefficients and I is the matrix of identities.
The characteristic equation is \(\(\begin{pmatrix} 5 & 1 \\ -26 & -5 \end{pmatrix}\)\) using the coefficient matrix.
\(\[\begin{vmatrix} 5 - \lambda & 1 \\ -26 & -5 - \lambda \end{vmatrix} = 0\]\)
Increasing the determinant's scope:
\(\((5 - \lambda)(-5 - \lambda) - (-26)(1) = 0\)\)
Simplifying:
\(\((\lambda - 5)(\lambda + 5) - 26 = 0\)\(\lambda^2 - 25 - 26 = 0\)\(\lambda^2 - 51 = 0\)\)
We obtain two eigenvalues after solving for :
\(\(\lambda_1 = \sqrt{51}\)\(\lambda_2 = -\sqrt{51}\)\)
Then, for each eigenvalue, we identify the matching eigenvectors.
If \(\(\lambda_1 = \sqrt{51}\):\((A - \lambda_1 I)v_1 = 0\)\)
Changing the values:
\(\((5 - \sqrt{51})v_1 + v_2 = 0\)\(-26v_1 + (-5 - \sqrt{51})v_2 = 0\)\)
We can use the free variable v_1 = 1 to solve these equations:
\(\(v_2 = \sqrt{51} - 5\)\)
As a result,\(\(v_1 = \begin{pmatrix} 1 \\ \sqrt{51} - 5 \end{pmatrix}\).\) is the eigenvector corresponding to _1 = sqrt(51).
In the same way, for \(\(\lambda_2 = -\sqrt{51}\):\((A - \lambda_2 I)v_2 = 0\)\)
Changing the values:
\(\((5 + \sqrt{51})v_3 + v_4 = 0\)\(-26v_3 + (-5 + \sqrt{51})v_4 = 0\)\)
We can use the free variable\(\(v_3 = 1\)\) to solve these equations:
\(\(v_4 = -\sqrt{51} - 5\)\)
As a result, \(\(v_2 = \begin{pmatrix} 1 \\ -\sqrt{51} - 5 \end{pmatrix}\).\) is the eigenvector corresponding to\(\(\lambda_2 = -\sqrt{51}\)\)
The system of equations general solution is denoted by the following notation:
\(\[x = c_1 \cdot e^{\sqrt{51}t} \cdot \begin{pmatrix} 1 \\ \sqrt{51} - 5 \end{pmatrix} + c_2 \cdot e^{-\sqrt{51}t} \cdot \begin{pmatrix} 1 \\ -\sqrt{51} - 5 \end{pmatrix}\]\)
where t stands for the independent variable (time) and c_1 and c_2 are arbitrary constants.
To learn more about Linear algebra:
https://brainly.in/question/54116586
#SPJ4
PLEASE HELP, WILL MARK BRAINLIEST IF RIGHT!!!!
Identify the coordinates of the image. Figure C has coordinates of M(0, -3), N(-6, 0), O(-7, -10), and P(-3, -9). What are the coordinates of its image after a 270∘ clockwise rotation?
Answers
HELP QUICK PLEASE!!!!

Answers
Answer:
41.8°, 138.2° and 401.8°
Step-by-step explanation:
Given the expression;
\(3sin^2x + 4sinx - 4 = 0\)
Let P = sinx
The expression becomes;
3P²+4P - 4 = 0
Factorize
3P²+6P-2P - 4 = 0
3P(P+2)-2(P+2) = 0
3P-2 = 0 and P+2 = 0
P = 2/3 and -2
When P = 2/3
sinx = 2/3
x = arcsin 2/3
x = arcsin 0.6667
x = 41.8 degrees
Also if P = -2
sinx = -2
x = arcsin (-2)
x will not exist in this case
To get other values of x
sin is positive in the second quadrant
x = 180 - 41.8
x = 138.2°
x = 360+41.8
x = 401.8°
Hence the values of x within the interval are 41.8°, 138.2° and 401.8°
are my answers correct?

Answers
Answer:
Partially. Your answer to a is correct but you used the wrong number for b.
Step-by-step explanation:
The amount of money you earn (profit) is taken after all of your expenses. You correctly calculated that Leo made $5000 in profit. Divide that by 40 instead of $12850. (answer: $125/hour)
the mean time to expose a single panel in a circuit-board plant is 2 minutes with a standard deviation of 1.5 minutes. (a) what is the natural coefficient of variation? (b) if the times remain independent, what will be the mean and variance of a job of 60 panels? what will be the coefficient of variation of the job of 60? (c) now suppose times to failure on the expose machine are exponentially distributed with a mean of 60 hours and the repair time is also exponentially distributed with a mean of 2 hours. what are the effective mean and cv of the process time for a job of 60 panels?
Answers
Main Answer:
(a)The natural coefficient of variation is approximately 75%.
(b)The coefficient of variation of the job of 60 panels is approximately 83.33%.
(c)The effective mean of the process time for a job of 60.
Supporting Question and Answer:
How do you calculate the mean and variance of a job with multiple panels when the times remain independent?
The mean of a job with multiple panels is obtained by multiplying the mean of a single panel by the number of panels. The variance of a job with multiple panels is equal to the variance of a single panel multiplied by the number of panels, assuming independence.
Body of the Solution:
(a) The natural coefficient of variation (CV) can be calculated by dividing the standard deviation by the mean and multiplying by 100 to express it as a percentage.
Given:
Mean = 2 minutes
Standard Deviation = 1.5 minutes
CV = (Standard Deviation / Mean) * 100
CV = (1.5 / 2) * 100
CV ≈ 75%
Therefore, the natural coefficient of variation is approximately 75%.
(b) If the times remain independent, the mean of a job of 60 panels can be calculated by multiplying the mean time for a single panel by the number of panels in the job.
Mean of a job of 60 panels = Mean of a single panel * Number of panels Mean of a job of 60 panels = 2 minutes * 60 Mean of a job of 60 panels = 120 minutes
The variance of a job of 60 panels is equal to the variance of a single panel multiplied by the number of panels, assuming independence.
Variance of a job of 60 panels = Variance of a single panel * Number of panels
Variance of a job of 60 panels = (Standard Deviation of a single panel)^2 * Number of panels
Variance of a job of 60 panels = (1.5 minutes)^2 * 60
Variance of a job of 60 panels = 2.25 minutes^2 * 60
Variance of a job of 60 panels = 135 minutes^2
The coefficient of variation (CV) of a job of 60 panels can be calculated by dividing the standard deviation of the job by the mean of the job and multiplying by 100.
CV = (Standard Deviation of the job / Mean of the job) * 100 CV = (sqrt(Variance of the job) / Mean of the job) * 100 CV = (sqrt(135 minutes^2) / 120 minutes) * 100 CV ≈ 83.33%
Therefore, the coefficient of variation of the job of 60 panels is approximately 83.33%.
(c) Given that the times to failure on the expose machine are exponentially distributed with a mean of 60 hours and the repair time is also exponentially distributed with a mean of 2 hours, we need to consider the effective mean and coefficient of variation (CV) for the process time of a job of 60 panels.
For exponential distributions, the mean (μ) is equal to the reciprocal of the rate parameter (λ), and the variance (σ^2) is equal to the reciprocal of the squared rate parameter (λ^2).
Mean time for a job of 60 panels = Mean of a single panel * Number of panels Mean time for a job of 60 panels = 2 minutes * 60 Mean time for a job of 60 panels = 120minutes.
Mean time for a job of 60 panels with exponential distributions = Mean time for a job of 60 panels / 60 (to convert minutes to hours) Mean time for a job of 60 panels with exponential distributions = 120 minutes / 60 Mean time for a job of 60 panels with exponential distributions = 2 hours
To calculate the effective mean, we add the mean time for the job (process time) and the mean repair time:
Effective Mean = Mean time for a job of 60 panels with exponential distributions + Mean repair time
Effective Mean = 2 hours + 2 hours
Effective Mean = 4 hours
To calculate the effective coefficient of variation (CV) for exponential distributions, it remains the same as the natural coefficient of variation.
Therefore, the effective mean of the process time for a job of 60.
To learn more about the mean and variance of a job with multiple panels when the times remain independent from the given link
https://brainly.com/question/25639778
#SPJ4
‼️WILL LIST BRAINLIEST ‼️Explain the Error: Jayme tells her friend that ordered pairs that have an x-coordinate of O lie on the x-axis. She uses the origin as an example. Describe Jayme s error and why that statement is false,

Answers
A school has 160 students. Only 120 students went to a dance the school had. What percent of students went to the dance?
Answers
Answer:
75%
Step-by-step explanation:
percentage = v1 divided by v2
\(p = \frac{120}{160} = 75\%\)
One side of a triangle is 10 feet long, the second side is 20 feet long. What is the
range of possible values for the third side of the triangle? Why?
Answers
The range for the length of the third side is it must be greater than 10 feet and less than 30 feet.
What is the condition for the sides of triangles?The triangle inequality states that the sum of the lengths of any two sides of a triangle must be greater than or equal to the length of the third side. That sum can equal the length of the third side only in the case of a degenerate triangle, one with collinear vertices.
The length of the third side had to be greater than the difference between the two given sides and less than the sum of the two given sides.
(20 – 10) < S <(20+ 10) ; 10< S < 30
Therefore, the range for the length of the third side is it must be greater than 10 feet and less than 30 feet.
To learn more about the triangles visit:
https://brainly.com/question/2773823.
#SPJ1
8* x + y + y; use x=9, and y = 10
Answers
Answer:
If we have 8 * x + y + y:
We have to first substitute in x and y where they should be:
=> 8 * 9 + 10 + 10
According to the order of operations(PEMDAS(parenthesis, exponents, multiplication, division, addition, subtraction, multiplication and division is you go from left to right order, and same with addition and subtraction.)), we do the multiplication first(8*9):
=> 72 + 10 + 10
Now we just add them up:
=> 92
The price paid for $90 jeans after a 45% discount is applied
$
Answers
Step-by-step explanation:
Answer:
$49.50
Step-by-step explanation:
90 · 45% = 40.5
90 - 40.5 = 49.5
9x - 3x = 3x(3) is it true
Answers
Answer:
It is not true since 9x - 3x = 6x and
3x(3) = 9x.
Answer:
Not true b/c
Step-by-step explanation:
9x-3x=6x
and3x(3)=9x
6x is not equal to 9x
On November 1, 2020 Starstruck Inc. signed a $300,000,8 month, 8% note payable. At due date, the principal and interest will be paid. Calculate the amount of interest expense that Starstruck Inc. should report on its income statement for the year ended December 31,2021. (round to the nearest dollar) Answer: \$.
Answers
Starstruck Inc. should report approximately $8,767 as the amount of interest expense on its income statement for the year ended December 31, 2021.
To calculate the amount of interest expense that Starstruck Inc. should report on its income statement for the year ended December 31, 2021, we need to determine the interest accrued for the 14-month period from November 1, 2020, to December 31, 2021.
The formula to calculate interest expense is:
Interest Expense = Principal * Interest Rate * Time
Principal = $300,000
Interest Rate = 8% per year
Since the note is an 8-month note, we need to calculate the interest for the 14-month period.
We can use the following formula to calculate the time in years:
Time = Number of days / Days in a year
Number of days from November 1, 2020 to December 31, 2021 = 426 days
Days in a year = 365 days
Time = 426 / 365
Now we can calculate the interest expense:
Interest Expense = $300,000 * 8% * (426 / 365)
Interest Expense ≈ $8,767.12
To know more about income statement refer here:
https://brainly.com/question/14890247#
#SPJ11
What is the electron geometry chart
Answers
The Electron Geometry Chart is a visual representation of the arrangement of electrons in a molecule. It is used to predict the molecular shape and the bond angles of a molecule based on its electron-group geometry.
Electron geometry is a term used to describe the arrangement of electron groups around a central atom in a molecule. This arrangement is important in determining the molecular shape and the bond angles of the molecule, which can affect its physical and chemical properties.
The Electron Geometry Chart provides a simple and visual way of understanding the arrangement of electrons in a molecule. It shows the number of electron groups surrounding a central atom and the shape that they form.
The chart also shows the bond angles between the electron groups and the central atom, which can be used to predict the molecular shape of the molecule.
The value of the Electron Geometry Chart lies in its ability to help students and scientists understand the relationship between the electron arrangement in a molecule and its molecular shape and bond angles.
By using the chart, students can develop a deeper understanding of molecular geometry and its impact on the physical and chemical properties of a molecule.
to know more about the electron geometry chart refer here
https://brainly.com/question/7558603#
#SPJ11
Write the number five million four thousand three hundred in standard form.
Answers
Answer:
5,004,300
Step-by-step explanation:
The chart shows pricing and payment options for two big-ticket items. A 4-column table titled Financing Options for Household Items has 2 rows. The first column is labeled Item with entries laptop computer, 18.3 CF refrigerator. The second column is labeled rent-to-own payments with entries 150 dollars a month for 12 months, 140 dollars a month for 12 months. The third column is labeled installment plan with entries 100 dollars and 83 cents a month for 12 months, 80 dollars and 67 cents a month for 12 months. The fourth column is labeled cash price with entries 1,000 dollars, 800 dollars. Which payment option would be best for the laptop and for the refrigerator? rent-to-own; installment installment; rent-to-own rent-to-own; rent-to-own save up and pay cash
Answers
Answer:
3006
Step-by-step explanation:
this is