8r+6=9r-7 solve for r
Answers
I think its r=13 hope this helps :)
Related Questions
27% of 140 =
Blank% of 500 = 90
32% of Blank = 8
Help meeeee
Answers
What is the difference?
-3 2/3 - (-2 1/4)
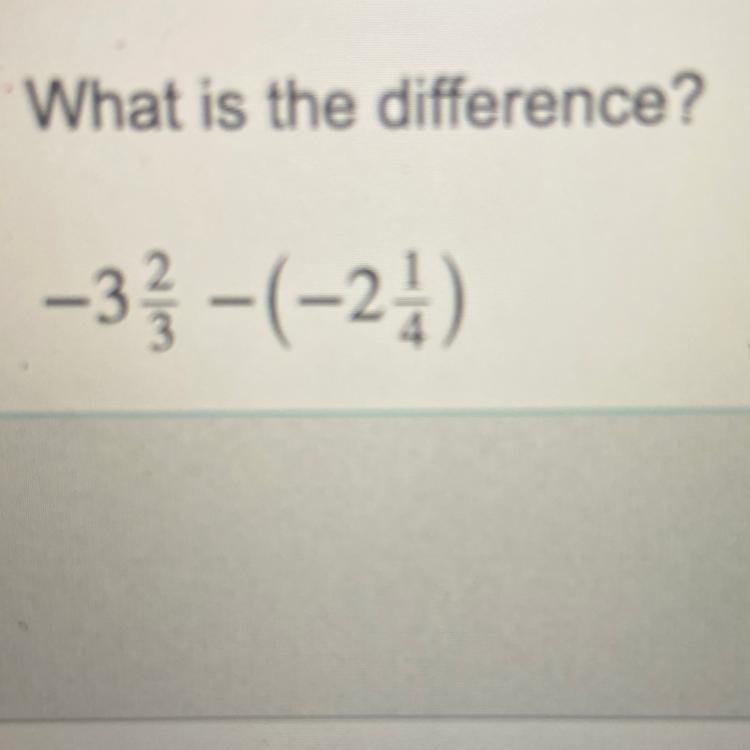
Answers
let's firstly convert the mixed fractions to improper fractions.
\(\stackrel{mixed}{3\frac{2}{3}}\implies \cfrac{3\cdot 3+2}{3}\implies \stackrel{improper}{\cfrac{11}{3}}~\hfill \stackrel{mixed}{2\frac{1}{4}} \implies \cfrac{2\cdot 4+1}{4} \implies \stackrel{improper}{\cfrac{9}{4}} \\\\[-0.35em] ~\dotfill\\\\ -\cfrac{11}{3}-\left( \cfrac{9}{4} \right)\implies -\cfrac{11}{3}+\cfrac{9}{4}\implies \cfrac{-(4)11~~ + ~~(3)9}{\underset{\textit{using this LCD}}{12}} \\\\\\ \cfrac{-44+27}{12}\implies \cfrac{-17}{12}\implies {\Large \begin{array}{llll} -1\frac{5}{12} \end{array}}\)
7. Based on an exponential model of the data, what is the predicted value of Variable 2 when
Variable 1 = 2?
Round your answer to the nearest whole number.
Variable 1:
10
20
30
40
50
60
70
80
90
100
variable 2:
100
80
52
40
35
25
17
11
10
7
Answers
Answer:
128
Step-by-step explanation:
You want a prediction for x=2 when the given data is modeled by an exponential model.
x = 10, 20, 30, 40, 50, 60, 70, 80, 90, 100y = 100, 80, 52, 40, 35, 25, 17, 11, 10, 7ModelA graphing calculator's exponential regression function models this data with the formula ...
y = 135.7 · 0.9711^x
y = 137.7 · 0.9711^2 ≈ 127.94 . . . . when x=2
This model gives a value for variable 2 of approximately 128 when variable 1 = 2.
<95141404393>

Help with trigonometry homework

Answers
By definition of tangent,
tan(A - π/4) = sin(A - π/4) / cos(A - π/4)
Expand the numerator and denominator using the angle sum identities for sin and cos:
tan(A - π/4) = (sin(A) cos(π/4) - cos(A) sin(π/4)) / (cos(A) cos(π/4) + sin(A) sin(π/4))
Divide through everything on the right by cos(A) cos(π/4):
tan(A - π/4) = (sin(A) / cos(A) - sin(π/4) / cos(π/4)) / (1 + (sin(A) sin(π/4)) / (cos(A) cos(π/4)))
Simplify the sin/cos terms to tan:
tan(A - π/4) = (tan(A) - tan(π/4)) / (1 + tan(A) tan(π/4))
tan(π/4) = 1, so we're left with
tan(A - π/4) = (tan(A) - 1) / (1 + tan(A))
Replace tan(A) with -√15:
tan(A - π/4) = (-√15 - 1) / (1 - √15)
Then the last option is the correct one.
can we say ((-16)÷4) ÷ (-2) is the same as (-16)÷ (4÷(-2)?
Answers
Answer:
no we can't
Step-by-step explanation:
(-4)÷(-2). (-16÷(-2)
2. 8
\(\longrightarrow{\blue{[( - 16)\div 4) \div ( - 2)] \:is\:not\:equal\:to\:( - 16) \div [4 \div( - 2) ] }}\)
\(\large\mathfrak{{\pmb{\underline{\orange{Step-by-step\:explanation}}{\orange{:}}}}}\)
\([( - 16 )\div 4) \div ( - 2)] = ( - 16) \div [4 \div( - 2) ]\)
Let us first solve for L. H. S.
\( = [( - 16 )\div 4) \div ( - 2)]\)
\( = [ (\frac{ - 16}{4} )\div ( - 2)]\)
\( = \frac{( - 4)}{( - 2)} \)
\( = 2\)
Now, R. H S.
\(( - 16) \div [4 \div ( - 2)]\)
\( = \frac{ - 16}{ - 2} \)
\( = 8\)
\(\sf\purple{L. H. S.\: ≠ \:R. H. S. }\)
Hence, \([( - 16) \div 4) \div( - 2)] ≠(-16)\div [4 \div( - 2) ]\)
\(\red{\large\qquad \qquad \underline{ \pmb{{ \mathbb{ \maltese \: \: Mystique35♛}}}}}\)
which is equal to (sinx+cosx)^2+(sinx-cosx)^2 using identities?
Answers
The expression (sinx + cosx)^2 + (sinx - cosx)^2 simplifies to
4 + 2sinxcosx.How to simplify the identityTo simplify the expression (sinx + cosx)^2 + (sinx - cosx)^2 using trigonometric identities, we can expand and simplify the expression.
Expanding the squared terms
(sin^2x + 2sinxcosx + cos^2x) + (sin^2x - 2sinxcosx + cos^2x)
Using the trigonometric identity sin^2x + cos^2x = 1, we can simplify further:
(1 + 2sinxcosx + 1) + (1 - 2sinxcosx + 1)
Simplifying the expression, we have:
2 + 2sinxcosx + 2
Combining like terms, we get:
4 + 2sinxcosx
Learn more about identities at
https://brainly.com/question/7331447
#SPJ1
Please help asap! For a test (25 points)
The diameter of a circle is 4 m. Find its area in terms of π.
Answers
Answer: 4\(\pi\) m^2
Step-by-step explanation:
The formula to calculate the area of a circle:
\(\pi r^{2}\)
Given that the diameter of a circle is 4, we can work out that r (the radius) is 2.
(The radius is half of the diameter)
Therefore we can plug in our values:
\(\pi 2^{2}\)
\(2^{2}\) = 4
Therefore your answer is:
\(4\pi\) \(m^{2}\)
(Remember your units!)
Answer: A=12.566
Step-by-step explanation:
A=πr^2
R=2
π*4=12.566
I don't know how you want the answer rounded so I just rounded it to the nearest thousandths
I WILL GIVE BRAINLIST FOR THE FIRST ANSWER
Albert is traveling 70 mph in his car. After 4 hours, how far will he have traveled?
A.
285 miles
B.
290 miles
C.
270 miles
D.
280 miles
Answers
Answer:
D.280 miles
Step-by-step explanation:
Albert is travelling 70mph (70 miles per hour).
So this can be worked out by:
70 x 4 hours= 280 miles
Answer:
D. 280
Step-by-step explanation:
if he is traveling 70 mph that means every hour he goes 70 miles so in 4 hours he will travel 280 miles
70 mph x 4 hours = 280 miles
A piece of wood is in the shape of a rectangular prism with a length of 10 inches, a width of 4 inches, and a height of 5 inches. You cut the wood in half to form two pieces of wood, each with a length of 5 inches. What is the percent increase in the total surface area? Round your answer to the nearest hundredth, if necessary. %
Answers
Answer: 18.18%
Step-by-step explanation:
First, let's calculate the surface area of the original piece of wood. The surface area (SA) of a rectangular prism is given by the formula:
\($$SA = 2lw + 2lh + 2wh$$\)
where \(\(l\)\) is the length, \(\(l\)\) is the width, and \(\(h\)\) is the height. For the original piece of wood, \(\(l = 10\) inches\), \(\(w = 4\) inches\), and \(\(h = 5\) inches\).
After the piece of wood is cut in half, the length becomes 5 inches, but the width and height remain the same. So, for each of the two new pieces of wood, \(\(l = 5\) inches\), \(\(w = 4\) inches\), and \(\(h = 5\) inches\). The total surface area of the two new pieces of wood is twice the surface area of one of the new pieces.
The percent increase in the total surface area is given by the formula:
\($$\text{Percent Increase} = \frac{\text{New Total SA} - \text{Original SA}}{\text{Original SA}} \times 100\%$$\)
Let's calculate these values.
The percent increase in the total surface area when the piece of wood is cut in half is approximately 18.18%.
Use synthetic division to evaluate for the indicated x value.
x³ + x²-3x +9; ƒ (-4)
f(-4)=
Answers
The first step to calculate the indicated x value using synthetic division is to assemble the synthetic division table, which will be:
Column 1 | Column 2-4 | 11 -3 91 -3 9 -63 |The first number on the top line, 1, is the coefficient of the highest degree term in the polynomial. The remaining coefficients are written in order, with 0 placeholders for any missing terms. The divisor, -4, is written to the left of the table.
How to calculate synthetic division?We must reduce the first coefficient, which is 1. Then we multiply -4 by 1 to get -4 and write that in the next coefficient, which is 1. We add the two numbers to get -3 , which we write under the next coefficient , which is -3. We multiply -4 by -3 to get 12 and write that under the last coefficient, which is 9. We add the two numbers together to get -51, which is the remainder.Therefore, we find ƒ(-4) = -51.
Find out more about synthetic division on:
https://brainly.com/question/24662212
#SPJ1
The polynomial
p(x)=24x3−46x2+29x−6
has three real roots. One of them is x=2/3 Find the others and list them in increasing sequence:
Answers
The other roots of the cubic equation p(x) = 24·x³ - 46·x³ + 29·x - 6 are;
x = 1/2
x = 3/4
What is a cubic equation in mathematics?A cubic equation is an equation that has 3 as the highest index.
The specified polynomial in the question is presented as follows;
P(x) = 24·x³ - 46·x² + 29·x - 6
The solution of the equation is; x = (2/3)
Therefore, (x - 2/3) is a factor of the equation and we get;
(24·x³ - 46·x² + 29·x - 6) ÷ (x - 2/3) has a remainder of 0
Dividing the above expression using long division, we get;
24·x² - 30·x + 9
(x - 2/3) \({}\) |(24·x³ - 46·x² + 29·x - 6)
\({}\) 24·x³ - 16·x² + 29·x - 6
\({}\) -30·x²
\({}\) -30·x² + 20·x
\({}\) 9·x - 6
\({}\) 9·x - 6
The other real roots of the specified equation can be found as follows;
The equation for the roots is; P(x) = 24·x³ - 46·x² + 29·x - 6 = 0
From the above long division, therefore;
24·x³ - 46·x² + 29·x - 6 = (24·x² - 30·x + 9) × (x - 2/3) = 0
Which indicates; (24·x² - 30·x + 9) = 0 or (x - 2/3) = 0
The other solution are;
24·x³ - 30·x + 9 = 0
3·(·8·x² - 10·x + 3) = 0
8·x² - 10·x + 3 = 0
Solutions for the above equation in the form; a·x² + b·x + c = 0 can be obtained using the quadratic formula as follows;
The quadratic formula; x = \(\dfrac{-b\pm\sqrt{b^2 - 4\cdot a\cdot c} }{2\cdot a}\)
By comparing the equation, 8·x² - 10·x + 3 = 0 to the equation, a·x² + b·x + c = 0, we get;
a = 8, b = -10, and c = 3
Therefore;
x = (10 ± √((-10)² - 4 × 8 × 3))/(2 × 8)
((-10)² - 4 × 8 ×3) = 2
Therefore;
x = (10 ± √((-10)² - 4 × 8 × 3))/(2 × 8) = (10 ± 2)/(16)
x = 3/4, and x = 1/2
Therefore, the other other roots in increasing sequence are;
x = 1/2 and x = 3/4
Learn more about cubic functions in algebra here:
https://brainly.com/question/20896994
#SPJ1
A survey found that women's heights are normally distributed with mean 63.6 in and standard deviation 2.5 in. A branch of the military requires women's heights to be between 58 in and 80 in.
a. Find the percentage of women meeting the height requirement. Are many women being denied the opportunity to join this branch of the military because they are too short or too tall?
b. If this branch of the military changes the height requirements so that all women are eligible except the shortest 1% and the tallest 2%, what are the new height requirements?
Answers
Answer:
(A)
Step-by-step explanation:
The survey follows of women's height a normal distribution.
The height of 98.51% of women that meet the height requirement are between 58 inches and 80 inches.
The new height requirements would be 57.7 to 68.6 inches
The given parameters are:
\mathbf{\mu = 63.5}μ=63.5 --- mean
\mathbf{\sigma = 2.5}σ=2.5 --- standard deviation
(a) Percentage of women between 58 and 80 inches
This means that: x = 58 and x = 80
When x = 58, the z-score is:
\mathbf{z= \frac{x - \mu}{\sigma}}z=
σ
x−μ
This gives
\mathbf{z_1= \frac{58 - 63.5}{2.5}}z
1
=
2.5
58−63.5
\mathbf{z_1= \frac{-5.5}{2.5}}z
1
=
2.5
−5.5
\mathbf{z_1= -2.2}z
1
=−2.2
When x = 80, the z-score is:
\mathbf{z_2= \frac{80 - 63.5}{2.5}}z
2
=
2.5
80−63.5
\mathbf{z_2= \frac{16.5}{2.5}}z
2
=
2.5
16.5
\mathbf{z_2= 6.6}z
2
=6.6
So, the percentage of women is:
\mathbf{p = P(z < z_2) - P(z < z_1)}p=P(z<z
2
)−P(z<z
1
)
Substitute known values
\mathbf{p = P(z < 6.6) - P(z < -2.2)}p=P(z<6.6)−P(z<−2.2)
Using the p-value table, we have:
\mathbf{p = 0.9999982 - 0.0139034}p=0.9999982−0.0139034
\mathbf{p = 0.9860948}p=0.9860948
Express as percentage
\mathbf{p = 0.9860948 \times 100\%}p=0.9860948×100%
\mathbf{p = 98.60948\%}p=98.60948%
Approximate
\mathbf{p = 98.61\%}p=98.61%
This means that:
The height of 98.51% of women that meet the height requirement are between 58 inches and 80 inches.
So, many women (outside this range) would be denied the opportunity, because they are either too short or too tall.
(b) Change of requirement
Shortest = 1%
Tallest = 2%
If the tallest is 2%, then the upper end of the shortest range is 98% (i.e. 100% - 2%).
So, we have:
Shortest = 1% to 98%
This means that:
The p values are: 1% to 98%
Using the z-score table
When p = 1%, z = -2.32635
When p = 98%, z = 2.05375
Next, we calculate the x values from \mathbf{z= \frac{x - \mu}{\sigma}}z=
σ
x−μ
Substitute \mathbf{z = -2.32635}z=−2.32635
\mathbf{-2.32635 = \frac{x - 63.5}{2.5}}−2.32635=
2.5
x−63.5
Multiply through by 2.5
\mathbf{-2.32635 \times 2.5= x - 63.5}−2.32635×2.5=x−63.5
Make x the subject
\mathbf{x = -2.32635 \times 2.5 + 63.5}x=−2.32635×2.5+63.5
\mathbf{x = 57.684125}x=57.684125
Approximate
\mathbf{x = 57.7}x=57.7
Similarly, substitute \mathbf{z = 2.05375}z=2.05375 in \mathbf{z= \frac{x - \mu}{\sigma}}z=
σ
x−μ
\mathbf{2.05375= \frac{x - 63.5}{2.5}}2.05375=
2.5
x−63.5
Multiply through by 2.5
\mathbf{2.05375\times 2.5= x - 63.5}2.05375×2.5=x−63.5
Make x the subject
\mathbf{x= 2.05375\times 2.5 + 63.5}x=2.05375×2.5+63.5
\mathbf{x= 68.634375}x=68.634375
Approximate
\mathbf{x= 68.6}x=68.6
Hence, the new height requirements would be 57.7 to 68.6 inches
I will be posting some questions if you get them right you get brainliest
*Me thinking of a question*
Which of the following numbers shows a 7 in both the hundreds and tenths places?
a. 47,270.0787
b. 32,172.7193
c. 68,207.8777
d. 49,703.7924
Also sorry that I'm only giving 10 points It's because i'm low on points
Answers
Answer:
A
Step-by-step explanation:
Answer:
A is the answer. got it.thanks babe
7.2x14.3 what is that?
Answers
Answer:
102.96
Step-by-step explanation:
Answer:
\(102.96\)
Step-by-step explanation:
7 . 2
× 14 . 3
___________
²2 . 16
²28 . 80
72 . 00
____________
¹1¹02.96
Therefor, the answer is 102.96
What is the domain of the function represented by this graph? the graph of a quadratic function y = x^2 – 4 with a minimum value at the point (0,-4) A. -2 ≤ x ≤ 2 B. x ≥ 4 C. x ≤ 0 D. all real numbers Reset
Answers
Domain of the function represented by the graph of a quadratic function y = \(x^2\) – 4 with a minimum value at the point (0,-4) is all real numbers.
The correct answer is option D.
To determine the domain of the quadratic function y = \(x^2\) - 4, we need to consider the x-values for which the function is defined. Since a quadratic function is defined for all real numbers, the domain of this function is "all real numbers."
Let's analyze the given function and its graph to understand why the domain is "all real numbers."
The function y = \(x^2\) - 4 represents a parabola that opens upward, which means it extends infinitely in both positive and negative x-directions. The vertex of the parabola is at the point (0, -4), indicating that the minimum value of the function occurs at x = 0.
Since there are no restrictions or limitations on the x-values for which the function is defined, the domain is unrestricted and encompasses all real numbers. In other words, the function can be evaluated and calculated for any real value of x, whether it is a negative number, zero, or a positive number.
For more such information on: quadratic function
https://brainly.com/question/29293854
#SPJ8
(6.2 x 10²) x (3.5 x 10³)
Answers
Answer:
\(21.7 x 10^5\)
Step-by-step explanation:
(6.2 x 10²) x (3.5 x 10³)
First, multiply the coefficients: 6.2 x 3.5 = 21.7.
Then, add the exponents: 10² x 10³ = 10^(2+3) = 10^5.
Therefore, the result is 21.7 x 10^5.
Answer:
3286000
Step-by-step explanation:

Answer the question with an algebraic expression.
The perimeter of a square is m meters. How long, in centimeters, is each side of the square?
Answers
The length of the square in centimetres in algebraic expression is 25m
How to find the side length of a square?The perimeter of a square is m meters.
The length of the each side of the square in centimetres can be represented in an algebraic expression as follows:
Therefore,
perimeter of a square = 4l
where
l = side lengthTherefore,
m = 4l
where
m = perimeter of the squarel = m / 4 meters.
Therefore, the side length of the square in centimetres is as follows:
1 meters = 100 cm
m / 4 meters = ?
cross multiply
length of the square in meters = m / 4 × 100
length of the square in meters = 100m / 4
length of the square in meters = 25m
learn more on square here: https://brainly.com/question/13379880
#SPJ1
Set up the appropriate equation to solve for the missing angle.

Answers
65^2 = 4,225
46^2 = 2,116
To find the missing angle, we must subtract 2,116 from 4,225 and then identify the difference’s square root.
4,225 - 2,116 = 2,109
√2,109 ≈ 45
Hence, x ≈ 45.
Answer:
Using the Pythagorean Theorem, we know x^2 + 46^2 is equal to 65^2. With that in mind, it is important to note:
65^2 = 4,225
46^2 = 2,116
To find the missing angle, we must subtract 2,116 from 4,225 and then identify the difference’s square root.
4,225 - 2,116 = 2,109
√2,109 ≈ 45
Hence, x ≈ 45.
Step-by-step explanation:
PLEASE HELP !! ILL GIVE BRAINLIEST !!

Answers
Answer:
<g = 129°
alternate interior angles
Step-by-step explanation:
hope this helps! :)
G is 129°
Angles g and f are vertical angles.
the image is to show why :)

how many solutions does the system of equations have?

Answers
Step-by-step explanation:
The ONE solution to this system of two lines is the point where the two lines cross at (1,4)
3x – 2 < 4
A. x < 2
B. x < -3
C. x < -2
D. x < 6
Answers
Answer: A. x < 2
Step-by-step explanation:
We will isolate the variable with inverse operations.
Given:
3x – 2 < 4
Add 2 to both sides of the equation:
3x < 6
Divide both sides of the equation by 3:
x < 2
A. x < 2
9. If the arc measure of MN = 87°, what is the measure of

Answers
The complete question:
If the arc measure of MN = 87°, what is the measure of angle ∠MON ?
Solution:
In the given circle, the required measure of the angle ∠MON is given as 87°.
What is an angle ?
An angle is a mathematical term, which we can define, when two straight lines or rays meet at a common endpoint. The common point is called the vertex of an angle. The word angle comes from a Latin word named ‘angulus,’.
Interior angles:- The inner angle made by the intersection of two polygonal sides.
Exterior angles:- The outer angle made by the intersection of two polygonal sides.
Here,
For the given circle, the measure of arc MN is given in the form of an angle of 87° which consists of an angle MNO,
So the measure of the section is equal to MON i.e. ∠MON = 87°
Thus, the required measure of the angle ∠MON is given as 87°.
To know more about angle check:
https://brainly.com/question/28451077
#SPJ1
Segment
A
B
‾
AB
has endpoints at
A
(
−
4
,
5
)
A(−4,5) and
B
(
12
,
13
)
.
B(12,13).
Determine the coordinates of point
C
C that lies on
A
B
‾
AB
such that
A
C
:
C
B
=
3
:
1
AC:CB=3:1
Answers
Answer:
12.5
Step-by-step explanation:
Lucas is selling ribbons to raise money for the Juvenile Diabetes Research Foundation. His expenses include $46 for materials, plus $0.02 per ribbon. If Lucas charges $0.25 per ribbon, how many ribbons does he need to sell to break even
Answers
Answer:
He needs to sell 200 ribbons to break even.
Step-by-step explanation:
The break even point is where the expenses are equal to the earnings, so you can write an expression that indicates that Lucas' expenses are equal to his earnings:
46+0.02x=0.25x
Now, you can solve for x to find the answer:
46=0.25x-0.02x
46=0.23x
x=46/0.23
x=200
According to this, the answer is that he needs to sell 200 ribbons to break even.
If the graph of y=-x^2 is translated horizontally 10 units to the right and translated vertically 3 units upwards, what is its new
equation?
Answers
Answer:
y=\((x-10)^{2}\)+3
Step-by-step explanation
in order to shift the equation to the right you must subtract a positive number from x (ex: -10)
to shift the equation upwards just add the positive number to the end of the equation (ex: +3)
What is 100 divided by the divine right of 10 to the power of 7
Answers
Step-by-step explanation:
100 ÷ 10⁷ = 10² ÷ 10⁷ = \(10^{-5}\) = 1/100.000
Let f(x) = 16 – x^2 , g(x) = 4 – x. Find (fg)(x) and its domain
Answers
Domain:(-oo,oo) these are infinity symbols by the way.
finding values of products and quotient functions
\(( \frac{r}{s} )(3) = \)
(3) = [/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/fo6qtw13QDITrL0XHWTkFEFXENPGcfQd.jpeg)
Answers
The product and the quotient of the functions are as follows:
(rs)(4) =8
(r / s)(3) = 2
How to solve function?A function relates input and output. It relates an independent variable with a dependent variable.
Therefore, let's solve the function as follows:
r(x) = 2√x
s(x) = √x
Therefore, let's find
(rs)(4) = r(4) × s(4) = 2√4 × √4 = 4 × 2 = 8
Let's find
(r / s)(3) = r(3) / s(3) = 2√3 / √3 = 2
Therefore,
(rs)(4) =8
(r / s)(3) = 2
learn more on function here: https://brainly.com/question/17430065
#SPJ1
-8/9 + (-2)/57
find the absolute value of the following rational number
Answers
The absolute value of the Rational number -474/513 is 474/513.
To find the sum of the rational numbers -8/9 and -2/57, you need to have a common denominator. The least common multiple (LCM) of 9 and 57 is 513. So, you can rewrite the fractions with a common denominator:
-8/9 = (-8/9) * (57/57) = -456/513
-2/57 = (-2/57) * (9/9) = -18/513
Now, you can add the fractions:
-456/513 + (-18/513) = (-456 - 18)/513 = -474/513
To find the absolute value of the rational number -474/513, you simply ignore the negative sign and take the value as positive:
| -474/513 | = 474/513
Therefore, the absolute value of the rational number -474/513 is 474/513.
For more questions on Rational .
https://brainly.com/question/30339525
#SPJ8
N/4 = 14 What is the value of n
Answers
Answer:
\( \frac{n}{4} = 14 \\ n = 4 \times 14 \\ n = 56\)