800 time 40 divided by 6 equals
Answers
Answer:
5333.33333333 is ur awnser
Step-by-step explanation:
Answer:
5333.33333
Step-by-step explanation:
800x40=32000
32000/6=5333.33333
Related Questions
if CD = 6.6 cm, DE = 3.4 cm, CE = 4.2 cm, and BC = 5.25 cm, what is the length of AC, the the nearest hundredth of a centimeter? 1. 2.70 2. 3.34 3. 5.28 4. 8.25

Answers
The value of length of AC is,
⇒ AC = 8.25
We have to given that;
CD = 6.6 cm, DE = 3.4 cm, CE = 4.2 cm, and BC = 5.25 cm
Now, We can formulate;
BC / AC = EC / CD
Substitute the values we get;
5.25 / AC = 4.2 / 6.6
Solve for AC;
5.25 x 6.6 / 4.2 = AC
AC = 8.25
Thus, The value of length of AC is,
⇒ AC = 8.25
Learn more about the divide visit:
https://brainly.com/question/28119824
#SPJ1
What is the value of tan O?
Answers
Answer:
In trigonometry, the value of tan 0 is 0. The word 'Trigonometry' is derived from the Greek word and the subject is developed to solve geometric problems involving triangles. It is used to measure the sides of a triangle.
Answer:
→ 0 (zero)
Step-by-step explanation:
The value of tan 0 is 0.
Solve the following equation for F. Be sure to take into account whether a letter is capitalized or not.

Answers
Answer:
F=M*H
Step-by-step explanation:
Steps:
Eliminate the fraction and isolate the F by multiplying both sides by H
a simple random sample of 400 individuals provides 124 yes responses. (a) what is the point estimate of the proportion of the population that would provide yes responses?
Answers
Answer:
Step-by-step explanation:
Given:
n= Total number of random sample of people taken=400
x= Number of people who provided yes responses= 124
P= The point of estimate of the sample of the population portion taken=?
Now,
P=x/n
P=124/400
P= 124/4×100
P= 32/100
P= 0.32 or 32%
#SPJ4
0.31 or 31% is the point estimate of the proportion of the population that would provide yes responses
What is meant by Estimate of Proportion?Estimate of Proportion: If we divide the random variable, the mean, and the standard deviation by n, we get a normal distribution of proportions with P′, called the estimated proportion, as the random variable. (Recall that a proportion as the number of successes divided by n.)
a simple random sample of 400 individuals provides 124 yes responses
The point estimate of individuals that would provide yes responses is the sample proportion.
n= Total number of random sample of people taken=400
x= Number of people who provided yes responses= 124
P= The point of estimate of the sample of the population portion taken
The sample proportion is calculated by dividing number of yes responses by sample size
p = x/n = 124/400= 0.31 or 31%
0.31 or 31% is the point estimate of the proportion of the population that would provide yes responses
To learn more about Estimate of Proportion visit:
brainly.com/question/17081600
#SPJ4
What is the tangent ratio of KJL? (Question and answers provided in picture.)

Answers
Answer:
Option (1)
Step-by-step explanation:
The given triangle JKL is an equilateral triangle.
Therefore, all three sides of this triangle will be equal in measure.
Side JK = JL = KL = 48 units
Perpendicular LM drawn to the base JK bisects the base in two equal parts JM and MK.
By applying tangent rule in ΔJML,
tan(∠KJL) = \(\frac{\text{Opposite side}}{\text{Adjacent side}}\)
= \(\frac{\text{LM}}{\text{JM}}\)
= \(\frac{\text{LM}}{24}\)
Since, Sin(K) = \(\frac{\text{Opposite side}}{\text{Hypotenuse}}\)
Sin(60)° = \(\frac{\text{LM}}{48}\)
\(\frac{\sqrt{3}}{2}=\frac{\text{LM}}{48}\)
LM = 24√3
Now, tan(∠KJL) = \(\frac{\text{LM}}{24}\)
= \(\frac{24\sqrt{3} }{24}\)
Therefore, Option (1) will be the answer.
Evaluate 18 -8(14 + 4) + 42.
Answers
Answer:
-84
Step-by-step explanation:
Use Descartes' Rule of Signs to determine how many positive and how many negative real zeros the polynomial can have. Then determine the possible total number of real zeros. (Enter your answers as comma-separated lists.)
P(x) = x^3 − x^2 − x − 5
number of positive zeros possible number of negative zeros possible number of real zeros possible
Answers
According to Descartes' Rule of Signs, there is 1 positive real zero and 2 or 0 negative real zeroes of the polynomial.
Descarte's Rule of Signs determines the number of real zeros in polynomial functions.
This indicates that -
The number of positive real zeros in the polynomial function f(x) is less than or equal to an even number depending on the sign change of the coefficients.
The number of negative real zeros in f(x) is an even number equal to or less than the number of sign changes of the coefficients of f(-x) terms.
Here, the polynomial function is given as -
\(P(x)=x^{3}-x^{2} -x-5\) ----- (1)
We have to find out the number of positive and negative real zeros that the given polynomial can have.
The given polynomial already has its variables in the descending powers. So, we can easily determine the number of sign changes in the coefficients of P(x).
So, the coefficients of the variables in P(x) are -
1, -1, -1, -5
From above, we see that -
There is a sign change in the first and second variable coefficients
There is no sign change in the second and third variable coefficients
There is no sign change in the third and fourth variable coefficients
According to Descartes' Rule of Signs, there can be exactly three positive real zeros or less than three but an odd number of zeros.
So, we can determine that the number of positive real zeroes of the given polynomial can be 1.
To find out the negative real zeroes of the given polynomial, we have to find out P(-x) and determine the sign changes in the variable coefficients of P(-x).
From equation (1), we can write P(-x) as -
\(P(x)=x^{3}-x^{2} -x-5\\= > P(-x)=(-x)^{3}-(-x)^{2} -(-x)-5\\= > P(-x)=-x^{3}-x^{2} +x-5\)----- (2)
So, the coefficients of the variables in P(-x) are -
-1, -1, +1, -5
From above, we see that -
There is no sign change in the first and second variable coefficients
There is a sign change in the second and third variable coefficients
There is a sign change in the third and fourth variable coefficients
According to Descartes' Rule of Signs, since there are two sign changes of the coefficient variables, there can be two negative real zeros or less than two but an even number of zeros.
So, we can determine that the number of negative real zeroes of the given polynomial can be 2 or 0.
Thus, according to Descartes' Rule of Signs, there is 1 positive real zero and 2 or 0 negative real zeroes of the polynomial.
To learn more about Descartes' Rule of Signs visit https://brainly.com/question/28747313
#SPJ4
A speed limit is 35 mph. A car is travelling 10 mph over the speed limit. I’d that a sum of 0
Answers
Answer:
The car is going 45 mph
Step-by-step explanation:
Since the speed limit is 35 mph and the car is 10 mph over the speed, we can add them to find out how fast the car is going. We can solve 35+10 which will give us 45. So it is not a sum of 0 but instead a sum of 45.
(hope this helped)
Answer:
35+10 =45
Step-by-step explanation:
add 10 to 35 then divide by 2
Convert, but do not evaluate, the following integral into cylindrical co- ordinates where E is the region in the first octant bounded by the cone z V3.x2 + 3y2, the paraboloid z = 6 – x2 - y², the xz- 2-plane and yz-plane. - - 2 2 !!! dV (.x2 + y2)1/2 E
Answers
The integral in cylindrical coordinates, but we are not required to evaluate it.
To convert the integral into cylindrical coordinates, we need to express the limits of integration and the volume element in terms of cylindrical coordinates.
In cylindrical coordinates, the region E is defined as:
0 ≤ θ ≤ π/2 (first octant)
0 ≤ r ≤ √(6cosθ + 3sin²θ) (intersection of cone and paraboloid)
0 ≤ z ≤ 6 - r²cos²θ - r²sin²θ (above xz-plane and inside cone and paraboloid)
The volume element in cylindrical coordinates is given by:
dV = r dz dr dθ
To see why, note that a small change in r, dr, results in a cylindrical shell of thickness dr, height dz, and radius r. The volume of this shell is given by 2πr dz dr, which is equal to r dz dr dθ after integrating over θ.
Substituting these expressions into the given integral, we get:
∫∫∫ E (x² + y²)^(1/2) dV
= ∫₀^(π/2) ∫₀^(√(6cosθ + 3sin²θ)) ∫₀^(6 - r²cos²θ - r²sin²θ) r (r²cos²θ + r²sin²θ)^(1/2) dz dr dθ
= ∫₀^(π/2) ∫₀^(√(6cosθ + 3sin²θ)) r (r²cos²θ + r²sin²θ)^(1/2) (6 - r²cos²θ - r²sin²θ) dr dθ
This is the integral in cylindrical coordinates, but we are not required to evaluate it.
To learn more about cylindrical visit:
https://brainly.com/question/28995951
#SPJ11
The sum of a number and the opposite of 3 equals 4
Answers
Assume that the number is x
The opposite of 3 is -3
Since the sum of the number and the opposite of 3 equals 4
Therefore:
\(x+(-3)=4\)Remember (+)(-) = (-), so
\(x-3=4\)To find x we need to move 3 to the other side by adding 3 to both sides
\(\begin{gathered} x-3+3=4+3 \\ x=7 \end{gathered}\)Since x represents the number, so
The number is 7
Let us check the answer
7 + -3 = 4
The answer is correct
Which set of ordered pairs represents y as a function of x?

Answers
Answer:
The third set of ordered pairs
Step-by-step explanation:
one x is paired with one y
Please help me I need ittttt

Answers
Answer:
B
Step-by-step explanation:

Answer:
B.
Step-by-step explanation:
You can easily read the point (2, 0).
Let's try each equation with point (2, 0).
A.
y = √x + 2
y = √2 + 2
y = 2.41
This is point (2, 2.41), not (2, 0), so this equation is not it.
B.
y = √(x - 2)
y = √(2 - 2)
y = 0
This is point (2, 0), so this equation may be it.
C.
y = √x - 2
y = √2 - 2
y = -0.586
This is point (2, -0.586), not (2, 0), so this equation is not it.
Answer: B.
PLEASE HELP!
*multiple choice*
List the sides in order from shortest to longest.
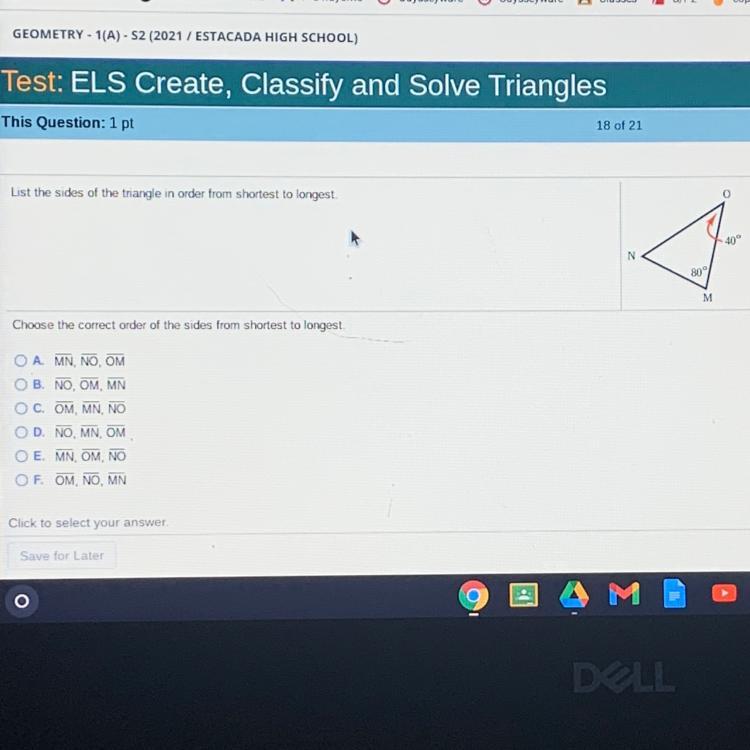
Answers
Answer:
I think it's a
I'm not that sure tho
help your girl outtt !!!

Answers
plz help I will mark brainliest :)

Answers
Answer:
6,008.3
Step-by-step explanation:
\(V=\pi r^{2} h\\V=\pi 7.5^{2} 34\)
Answer:
2nd one is the nearest tenth
Step-by-step explanation:
V=πr²h
Solving it
V=22/7×7.5×7.5×34
V=6010.714286 cm ³
Plzzzz help! i will give brainliest 100 points! Let f(x) = 8x3 + 16x2 − 15 and g(x) = 2x + 1. Find f of x over g of x. A. 4 times x squared plus 6 times x minus 3 plus 12 over the quantity 2 times x plus 1 B. 4 times x squared plus 6 times x plus 3 plus 12 over the quantity 2 times x plus 1 C. 4 times x squared plus 6 times x minus 3 minus 12 over the quantity 2 times x plus 1 D. 4 times x squared plus 6 times x plus 3 minus 12 over the quantity 2 times x plus 1
Answers
Answer:
C. 4 times x squared plus 6 times x minus 3 minus 12 over the quantity 2 times x plus 1
Step-by-step explanation:
f(x) = 8x^3 + 16x^2 − 15
g(x) = 2x + 1.
f(x) / g(x) = (8x^3 + 16x^2 − 15) / (2x + 1)
Using long division

Answer:
4 times x squared plus 6 times x minus 3 minus 12 over the quantity 2 times x plus 1
Step-by-step explanation:
i did the test
PLSS HELP!!!!!! like this is part of my grade

Answers
Answer:
387 is rounded to 400
Step-by-step explanation:
Answer:
400
Step-by-step explanation:
0-49 = round down
50-99 = round up
Since 718 is between 0-49, we would round to 700
Since 331 is between 0-49, we would round to 300
700 - 300 = 400
g(n)=1+5(n−1)
Complete the recursive formula of g(n)=g(n−1)+ ?
Answers
The recursive formula which correctly represents the given formula; g ( n ) = g ( n − 1 ) + 5.
What is the recursive formula for the given arithmetic progression?It follows from the task content that the expression which represents the recursive formula.
By observation, the common difference, d of the arithmetic progression is; 5.
On this note, the recursive formula can be written as follows;
g ( n ) = g ( n − 1 ) + 5.
Consequently, the required recursive formula for the given arithmetic progression is; g ( n ) = g ( n − 1 ) + 5.
Read more on recursive formula;
https://brainly.com/question/15403068
#SPJ1
Use the properties of equality to find the value of x in this equation.
4(6x – 9.5) = 46
x = –1.5
x = 0.3
x = 1.79
x = 3.5
Answers
Answer:
x = 3.5
Step-by-step explanation:
4(6x - 9.5) = 46 ← divide both sides by 4
6x - 9.5 = 11.5 ← add 9.5 to both sides
6x = 21 ← divide both sides by 6
x = 3.5
If f(x) is parallel to the line y= 3/4 x + 2/5 which function could be f(x)
Answers
Answer:
If f(x) is parallel to the line y=3/4x+b ,it would have to have the same slope.
In this equation:
y=mx+b
m= is the slope of the line.
A line parallel to the line y=3/4x +2/5 must have the same slope; that it is to say, the slope would be m=3/4
Examples:
y=3/4 x+ 50000
y=3/4 x -51/36
y=3/4 x -√2
These functions could be parallels to the line y=3/4 x +2/5
Answer:
see below.
Step-by-step explanation:
The key to this question is the factor 3/4. So anything that is going to make the coefficient in front of x = to 3/4 is a possible answer.
y = 3/4x + b where b is anything but 2/5 is one answer. Disguised but still likely is
4y = 3x + b Where you could divide everything by 4
y = 3/4x + b/4
Even something like
-4y = - 3x + b is possible because when you divide by -4, you get
y = -3x/-4 + b/-4
y = 3x/4 - b/4
2.7 A 3400-lb car is traveling in third gear (overall gear reduction ratio of 2.5 to 1) on a level road at its top speed of 130 mi/h. The air density is 0.00206 slugs/ft3 . The car has a frontal area of 19.8 ft2 , a drag coefficient of 0.28, a wheel radius of 12.6 inches, a drive axle slippage of 3%, and a drivetrain efficiency of 88%. At this vehicle speed, what torque is the engine producing and what is the engine speed (in revolutions per minute)?
Answers
Answer:
1) The engine torque is approximately 134.33 N·m
2) The speed of the engine is approximately 4,469.15 revolutions per minute
Step-by-step explanation:
1) The drag coefficient, \(c_d\), is given by the formula;
\(c_d = \dfrac{2 \cdot F_d}{\rho \cdot u^2 \cdot A}\)
Where;
\(c_d\) = 0.28
\(F_d\) = The drag force
ρ = The fluid density = 0.00206 slugs/ft³ = 1.06168037 kg/m³
u = The object's flow speed = 130 mi/h = 58.1152 m/s
A = The frontal area = 19.8 ft² = 1.83948 m²
\(F_d = \dfrac{c_d \cdot \rho \cdot u^2 \cdot A }{2}\)
∴ \(F_d\) = (0.28 × 1.06168037 × (58.1152)² × 1.83948)/2 ≈ 923.4 N
We have;
\(F_d = \dfrac{M_e \cdot \varepsilon _0 \cdot \eta _d }{r}\)
Where;
\(M_e\) = The engine torque
ε₀ = The overall gear reduction ratio = 2.5
\(\eta _d\) = The drivetrain efficiency = 0.88
r = The wheel radius = 12.6 inches = 0.32004 meters
\(\therefore M_e = \dfrac{F_d \cdot r }{ \varepsilon _0 \cdot \eta _d}\)
\(\therefore M_e = \dfrac{F_d \cdot r }{ \varepsilon _0 \cdot \eta _d} \approx \dfrac{923.4 \times 0.32004 }{ 2.5 \times 0.88} \approx 134.33 \ N\cdot m\)
The engine torque = \(M_e\) ≈ 134.33 N·m
The engine torque ≈ 134.33 N·m
2) The speed of the engine, \(n_e\), is obtained from the following formula;
\(v = \dfrac{2 \cdot \pi \cdot r \cdot n_e \cdot (1 - i)}{\varepsilon _0}\)
Where;
v = The vehicle's speed = 130 mi/h = 58.1152 m/s
r = The wheel radius = 12.6 inches = 0.32004 meters
i = The drive axle slippage = 3% = 3/100 = 0.03
ε₀ = The overall gear reduction ratio = 2.5
\(\therefore n_e = \dfrac{v \times \varepsilon _0 }{2 \times \pi \times r \times (1 - i)} = \dfrac{58.1152 \times2.5 }{2 \times \pi \times 0.32004 \times (1 - 0.03)} \approx 74.486 \ rev /second\)
The speed of the engine in revolution per minute = 60 seconds/minute × 74.486 rev/second ≈ 4,469.15 revolutions per minute
The speed of the engine ≈ 4,469.15 revolutions per minute.
Let the joint probability mass function of X and Y be defined by P(X=x,Y=y)= 21
x+y
,x=1,2,3,y=1,2. Find E[XY] and E[X].
Answers
The expected value of the random variable XY is E[XY] = 7/3, and the expected value of the random variable X is E[X] = 5/3.
To calculate the expected value of XY, we need to find the sum of the product of XY and their respective probabilities for all possible values of X and Y. Using the provided joint probability mass function, we have:
E[XY] = ΣΣ (XY) * P(X=x, Y=y)
To simplify the calculation, we can consider the possible values of X and Y. The given range is x = 1, 2, 3 and y = 1, 2. Evaluating each term:
E[XY] = (1*1) * P(X=1, Y=1) + (1*2) * P(X=1, Y=2) +
(2*1) * P(X=2, Y=1) + (2*2) * P(X=2, Y=2) +
(3*1) * P(X=3, Y=1) + (3*2) * P(X=3, Y=2)
Substituting the joint probability mass function P(X=x, Y=y) = 2/(x+y), we can calculate each term and simplify:
E[XY] = (1*1) * 2/2 + (1*2) * 2/3 +
(2*1) * 2/3 + (2*2) * 2/4 +
(3*1) * 2/4 + (3*2) * 2/5
E[XY] = 7/3
To find E[X], we need to calculate the expected value of X. We can sum the product of X and its respective probability for each value of X:
E[X] = Σ (X) * P(X=x)
E[X] = (1) * P(X=1) + (2) * P(X=2) + (3) * P(X=3)
Substituting the joint probability mass function P(X=x, Y=y) = 2/(x+y), we can calculate each term and simplify:
E[X] = (1) * (2/2 + 2/3 + 2/4) + (2) * (2/3 + 2/4 + 2/5) + (3) * (2/4 + 2/5)
E[X] = 5/3
Therefore, the expected value of XY is E[XY] = 7/3, and the expected value of X is E[X] = 5/3.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
If in a population of 100 individuals, the allele frequency of the dominant allele is 0.8, how many homozygous dominant individuals are there? a. 64 b. 32 c. 16 d. 80
Answers
The answer is 64. To find the number of homozygous dominant individuals in the population.
We need to use the Hardy-Weinberg equation:
p^2 + 2pq + q^2 = 1
Where:
p = frequency of dominant allele
q = frequency of recessive allele
Since the dominant allele frequency is 0.8, we can assume that the recessive allele frequency is 0.2 (since p + q = 1).
To find the frequency of homozygous dominant individuals (p^2), we simply square the frequency of the dominant allele:
p^2 = (0.8)^2 = 0.64
To find the number of homozygous dominant individuals, we multiply the frequency by the total population size:
0.64 x 100 = 64
Therefore, there are 64 homozygous dominant individuals in the population.
Learn more about dominant here:
https://brainly.com/question/30418951
#SPJ11
Solve the system.
x - 5y + 4z=27
4x-3y-z-23
3x + 3y - 6z=-9
Answers
Answer:
Step-by-step explanation:
Step by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method x-5y+4z=27,4x-3y-z=23,3x+3y-6z=-9 Tiger Algebra Solver.
how can confidence intervals help researchers attain their purpose of using a sample to understand a population?
Answers
The reason for why the confidence intervals help researchers attain their purpose of using a sample to understand a population is given below .
In the question ,
we have been asked how does the confidence interval help researchers to attain the purpose of using a sample to understand a population ,
we know that , the confidence interval is calculated from an estimate of how far away our sample mean is from actual population mean .
the confidence interval are useful because ,
(i) by calculating the confidence intervals around any data we collect, we have additional information about the likely values we are trying to estimate .
(ii) they make data analyses richer and help us to make more informed decisions about the research questions .
Therefore , the reason how confidence interval helps is mentioned above.
Learn more about Confidence Interval here
https://brainly.com/question/20309162
#SPJ4
What is the product of -2x^3+x-5 and x^3-3x-4?
(A) Show your work.
(B) Is the product equal to (x^3-3x-4)*(-2x^3+x-5)? Explain your answer.
Answers
Answer:(A) Show your work.
Step-by-step explanation:(A) Show your work.
Answer: holy math sucks but check the explanation i gotchu
Step-by-step explanation: A) -2x^6 + 3x^5 - 2x^4 - 15x^3 + 4x^2 -20x - 20
B) No, the product is not equal to (x^3-3x-4)*(-2x^3+x-5). This is because the order of the terms in the product is different than the order of the terms in the expression. The product takes the form of -2x^6 + 3x^5 - 2x^4 - 15x^3 + 4x^2 -20x - 20, whereas the expression has the form of (-2x^3+x-5)*(x^3-3x-4).
express as a trinomial (x−3)(2x−5)
Answers
The trinomial expression of (x−3)(2x−5) is 2\(x^{2}\) − 11x + 15.
To express the product of two binomials (x−3) and (2x−5) as a trinomial, we can use the FOIL method or distributive property.
FOIL stands for First, Outer, Inner, Last. We multiply the First terms in each binomial, then the Outer terms, then the Inner terms, and finally the Last terms. We then add these four products together to get our trinomial.
Using the distributive property, we can multiply each term in the first binomial by each term in the second binomial. This gives us four terms, which we can then simplify by combining like terms to obtain the trinomial.
So, using either method, we get:
(x−3)(2x−5) = x(2x) + x(-5) - 3(2x) - 3(-5)
= 2\(x^{2}\) -5x -6x + 15
= 2\(x^{2}\) − 11x + 15
To learn more about trinomial here:
https://brainly.com/question/23796911
#SPJ1
QUICK its the middle one

Answers
Answer:
25000000 should be the answer
Step-by-step explanation:
...
I have 8 questions witch means 80 points answer correctly!

Answers
\( \Large \pink{\tt \dfrac{35}{36}}\)
Solution :\( \tt \dfrac{3}{4} + \dfrac{2}{9}\)
By taking LCM = 4 × 9 = 36
\( \tt = \dfrac{3 \times 9}{4 \times 9} + \dfrac{2 \times 4}{9 \times 4}\)
\( \tt = \dfrac{27}{36} + \dfrac{8}{36}\)
\( \tt = \dfrac{27 + 8}{36}\)
\( \tt = \dfrac{35}{36}\)
\( \pink{\tt \therefore \: Answer \: is \: \dfrac{35}{36}}\)
Rich Is attending a 4-year college. As a freshman, he was approved for a 10-year, federal unsubsidized student loan in the amount of $7,900 at 4.29%. He knows he has the option of beginning repayment of the loan in 4.5 years. He also knows that during this non-payment time, interest will accrue at 4.29%.
Rich made his last monthly interest-only payment on November 1. His next payment Is due on December 1. What will be the amount of that Interest-only payment?
Answers
Rich will incur interest totaling $1,525.095 throughout the course of the 4.5-year non-payment period.
What is interest rate?The amount of interest due each period expressed as a percentage of the amount lent, deposited, or borrowed is known as an interest rate. The total interest on a loaned or borrowed sum is determined by the principal amount, the interest rate, the frequency of compounding, and the period of time the loan, deposit, or borrowing took place.
Given that he is aware that he has the option to start loan payback in 4.5 years at the current interest rate of 4.29% on a $7,900 loan, the following will apply:
4.29% of 7900 after the first year
\(4.29/100*7900\)
=338.91
So, after the tenure of 4.5 years, to find total interest, the interest will be multiplied by 4.5:
=338.91*4.5
=1525.095
To learn more about interest rate refer to:
https://brainly.com/question/20690803
#SPJ1