8. Two straight lengths of wire are placed on the ground, forming vertical angles. If the measure (3 points)
of one of the angles formed is 72°, what are the measures of the other three angles? Explain
your answer.
Answers
See attachment
72 was given, and it is a vertical angle so it’s vertical angle is congruent (same) 72.
You can find the other missing angles with supplementary angle theory, two angles will equal 180 degrees, so 180 - 72 = 108.
The 108 angle is also a vertical angle so it’s vertical angle is also 108 degrees.

Related Questions
Seven more than the product of five and a number is 45.
Answers
Answer:
7+(5n)=45
n= 7.6
Step-by-step explanation:
Which of the following statements is true for a function with equation f(x) = 5(3)x?
Answers
The graph has y-intercept (0,5) and increases with a constant ratio of 3.
What is the function?A function in mathematics is a connection between a set of inputs (sometimes referred to as the domain) and a set of outputs (also referred to as the range). Each input value is given a different output value.
The y-intercept lies at (0, 5) because the value of the function at x=0 is 530 = 5. The 'constant ratio' is 3, meaning that any increment of 1 in x causes the function value to grow by a factor of 3. (That serves as the exponential term's foundation.)
Learn more about function:https://brainly.com/question/30721594
#SPJ1
Missing parts;
Which of the following statements is true for a function with equation f(x) = 5(3)*?
The graph has y-intercept (0,5) and increases with a constant ratio of 3.
The graph has y-intercept (0, 3) and decreases with a constant ratio of 3.
The graph has y-intercept (0, 3) and increases with a constant ratio of 5.
The graph has y-intercept (0,5) and decreases with a constant ratio of 3.

a class must have 65% of its capacity order cancelled the class holds 25 students if 16 students have enrolled how many more students need to enroll for the class to be held
Answers
Answer:
Your answer is 1 more student.
Step-by-step explanation:
For the class to be held it need 16.25 students.
I got that number by multiplying 25 by .65
Because we can't have .25 of a student, and were talking about the minimum requirement. Having less than 16.25 would mean that we wouldn't have the class, so we need 17 students.
A construction engineer needs to
make sure a ceiling beam is
parallel to its corresponding
floor beam. Based on the
drawing, which pair of
measurements is sufficient
to show the beams are
parallel?
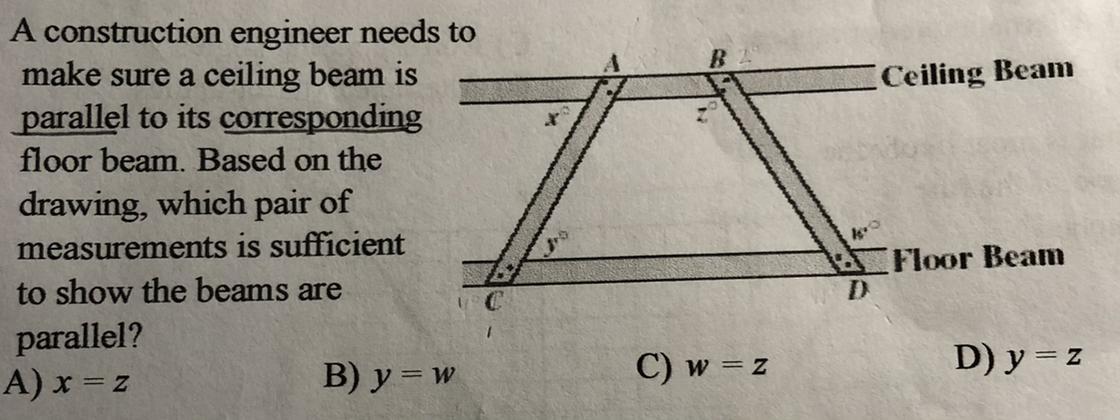
Answers
Answer:d
Step-by-step explanation:
if a wave has a wavelength of 25.4 cm and a frequency of 1.63 khz, its speed is closest to
Answers
Its speed is closest to 414m/s
given that
A waveform signal that is carried in space or down a wire has a wavelength, which is the separation between two identical places (adjacent crests) in the consecutive cycles. This length is typically defined in wireless systems in metres (m), centimetres (cm), or millimetres (mm) (mm). The wavelength is more frequently described in nanometers (nm), which are units of 10-9 m, or angstroms (), which are units of 10-10 m, for infrared (IR), visible light (UV), and gamma radiation ().
Frequency, which is defined as the quantity of wave cycles per second, and wavelength have an inverse relationship. The wavelength of the signal decreases with increasing signal frequency.
a wave has a wavelength = 25.4cm
a frequency = 1.63khz
now, we need to find speed of the wave
speed = wavelength × frequency
speed = 25.4 × 16.3
= 414m/s
speed = 414m/s
To learn more about wavelength:
https://brainly.com/question/13533093
#SPJ4
London is deciding between two truck rental companies. Company A charges an initial fee of $40 for the rental plus $2.50 per mile driven. Company B charges an initial fee of $100 for the rental plus $1 per mile driven. Let A represent the amount Company A would charge if London drives x miles, and let B represent the amount Company B would charge if London drives x miles. Write an equation for each situation, in terms of x, and determine the interval of miles driven, x, for which Company A is cheaper than Company B.
Answers
Using linear functions, we have that Company A is cheaper than Company B for distances of less than 40 miles.
What is a linear function?A linear function is modeled by:
y = mx + b
In which:
m is the slope, which is the rate of change, that is, by how much y changes when x changes by 1.b is the y-intercept, which is the value of y when x = 0, and can also be interpreted as the initial value of the function.For this problem, we consider that:
The slope is the cost per mile.The intercept is the initial fee.Hence the functions are:
A(x) = 40 + 2.50x.B(x) = 100 + x.Company A is cheaper when:
A(x) < B(x)
40 + 2.5x < 100 + x
1.5x < 60
x < 60/1.5
x < 40.
For distances of less than 40 miles, company A is cheaper.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
The table below shows some of the values of y = x2 + x − 4 for values of x from –3 to 3.
(a) Complete the table by finding the values of y for x = –1 and for x = 1.

Answers
Answer:
When x=-1, y=x^2+x-4 is -4. When x=1, y=x^2+x-4 is -2.
Step-by-step explanation:
First, insert the value of x into the equation.
y=-1^2+-1-4
Then, solve for y.
y=-1^2+-1-4
(Any negative squared is always a positive!)
y=1-1-4
y=0-4
y=-4
Repeat this to find the value of y when x=1.
y=1^2+1-4
(Remember, 1 to the power of anything is always 1.)
y=1+1-4
y=2-4
y=-2
Use cylindrical coordinates to evaluate ∭E√x2+y2dV, where E is the region that lies inside the cylinder x2+y2=16 and between the planes z=−5 and z=4.
Answers
The value of the triple integral is 72π.
To evaluate this triple integral in cylindrical coordinates, we first need to express the region E using cylindrical coordinates.
The cylinder x² + y² = 16 can be expressed in cylindrical coordinates as r² = 16, or r = 4. The planes z = -5 and z = 4 define a region of height 9.
So, the region E can be expressed in cylindrical coordinates as:
4 ≤ r ≤ 4
-5 ≤ z ≤ 4
0 ≤ θ ≤ 2π
The integrand √(x² + y²) can be expressed in cylindrical coordinates as r, so the integral becomes:
∭E√x²+y²dV = ∫0²π ∫4⁴ ∫-5⁴ r dz dr dθ
Note that the limits of integration for r are from 0 to 4, which means we are only integrating over the positive x-axis. Since the integrand is an even function of x and y, we can multiply the result by 2 to get the total volume.
The integral with respect to z is easy to evaluate:
∫₋₅⁴ r dz = r(4 - (-5))
= 9r
So the triple integral becomes:
∭E√x²+y²dV = 2 ∫0^2π ∫4⁴ 9r dr dθ
= 2(9) ∫0^²π 4 dθ
= 72π
Therefore, the value of the triple integral is 72π.
To know more about cylindrical check the below link:
https://brainly.com/question/23935577
#SPJ4
Find the volume of a right circular cone that has a height of 3.2 m and a base with a
radius of 14.1 m. Round your answer to the nearest tenth of a cubic meter.
Answers
Answer:
what's the question i need more info
(refer to figure 26, area 2.) the visibility and cloud clearance requirements to operate vfr during daylight hours over the town of cooperstown between 1,200 feet agl and 10,000 feet msl are
Answers
The visibility requirement is 3 statute miles, and cloud clearance requires maintaining 500 feet below, 1,000 feet above, and 2,000 feet horizontally from clouds during VFR daylight operations over Coopers Town.
Determine how to find the visibility and cloud clearance requirements to operate VFR?The visibility and cloud clearance requirements to operate VFR during daylight hours over the town of Coopers Town between 1,200 feet AGL and 10,000 feet MSL are as follows:
1. Visibility: The minimum visibility required is 3 statute miles.
2. Cloud clearance: Maintain a distance of at least 500 feet below, 1,000 feet above, and 2,000 feet horizontally from clouds.
According to VFR regulations, pilots flying during daylight hours must adhere to certain visibility and cloud clearance requirements for safety. The visibility requirement of 3 statute miles means that the pilot must have a clear horizontal view of at least 3 miles ahead.
This ensures sufficient visual reference to navigate and avoid other aircraft or obstacles.
Regarding cloud clearance, pilots must maintain a safe distance from clouds to ensure visibility and separation from potential hazards. The requirement is to remain at least 500 feet below clouds to avoid inadvertently entering them.
Additionally, pilots must maintain a minimum of 1,000 feet above clouds to prevent the risk of collision or reduced visibility due to cloud turbulence. Lastly, a horizontal separation of 2,000 feet from clouds helps ensure adequate maneuvering space and visual reference in relation to cloud formations.
These visibility and cloud clearance requirements help maintain safety and situational awareness for VFR operations during daylight hours over Coopers Town.
To know more about Cloud clearance, refer here:
https://brainly.com/question/31665470#
#SPJ4
Help me solve this please

Answers
Answer:
180 - 90 - 41 = 49
Step-by-step explanation:
Have a great day :)
Answer: 49
Step-by-step explanation:
90 + 41 + G = 180
131 + G = 180
G = 49
Find the area under the standard normal curve to the right of z=0. 69. Round your answer to four decimal places, if necessary. Answer1 Point- Tables- Keypad- Keyboard ShortcutsIf you would like to look up the value in a table, select the table you want to view, then either click the cell at the intersection of the row and column or use the arrow keys to find the appropriate cell in the table and select it using the Space key.
Answer Normal Table −[infinity] to −z
Answers
The area under the standard normal curve to the right of z = 0.69 is approximately 0.2451.
How to calculate the valueUsing a standard normal table:
Locate the row for 0.6 in the left-hand column of the table and the column for 0.09 along the top row of the table.
The intersection of the row and column gives the area to the left of z = 0.69, which is 0.7549.
Subtract this area from 1 to find the area to the right of z = 0.69:
area to the right of z = 0.69 = 1 - 0.7549 = 0.2451
Learn more about normal distribution on
https://brainly.com/question/4079902
#SPJ4
Help me please please

Answers
Answer:
No
Step-by-step explanation:
According to the attached table, his taxes would be around 22%
Then
$68300 * (1 - 0.22) = $53.274
coordinates (5,-7). What are its coordinates after it is rotated 180 about the origin?
Answers
The point (5,-7) after it is rotated 180 degrees about the origin becomes (-5,7).
What are coordinates?A coordinate is a group of numbers used to specify where a point or other geometric object is located in space. It is employed to find locations in space or a plane. Numerous branches of mathematics, physics, engineering, and other sciences use the coordinate system.
When a point is rotated 180 degrees about the origin, it means that the point is flipped directly across the origin to the opposite side.
In order to find the new coordinates of a point after it is rotated 180 degrees about the origin, we simply need to take the opposite of the original x and y coordinates.
So, for the point (5, -7), the new x-coordinate would be -5, which is the opposite of 5, and the new y-coordinate would be 7, which is the opposite of -7. Therefore, the point (5,-7) after it is rotated 180 degrees about the origin becomes (-5,7).
Learn more about coordinates on:
https://brainly.com/question/27996657
#SPJ4
38. let n be a positive integer whose decomposition into prime factors has no repeated prime. let b = {x | x is a divisor of n}. for example, if n = 21 = 3•7, then b = {1, 3, 7, 21}. let the following operations be defined on b: x + y = lcm(x, y) x • y = gcd(x, y) x′ = n/x then + and • are binary operations on b and ′ is a unary operation on b. 38a. for n=21,find {15 pts total; answer parts i. - v.} (i) 3 • 7 (ii) 7 • 21 (iii) 1 + 3 (iv) 3 + 21 (v) 3′
Answers
For all positive integer, (i) The result of 3 • 7 is 1. (ii) The result of 7 • 21 is 7. (iii) The result of 1 + 3 is 3. (iv) The result of 3 + 21 is 21. (v) The result of 3′ is 7.
(i) 3 • 71
To find the result of 3 • 7, we need to calculate the greatest common divisor (gcd) of 3 and 7.
The gcd(3, 7) = 1, which means that the only positive integer that divides both 3 and 7 without leaving a remainder is 1.
The result of 3 • 7 is 1.
(ii) 7 • 21
7
To find the result of 7 • 21, we need to calculate the gcd of 7 and 21.
The gcd(7, 21) = 7, which means that the only positive integer that divides both 7 and 21 without leaving a remainder is 7.
The result of 7 • 21 is 7.
(iii) 1 + 3
3
To find the result of 1 + 3, we need to calculate the least common multiple (lcm) of 1 and 3.
The lcm(1, 3) = 3, which means that the smallest positive integer that is divisible by both 1 and 3 is 3.
The result of 1 + 3 is 3.
(iv) 3 + 21
21
To find the result of 3 + 21, we need to calculate the lcm of 3 and 21.
The lcm(3, 21) = 21, which means that the smallest positive integer that is divisible by both 3 and 21 is 21.
The result of 3 + 21 is 21.
(v) 3′
7\
To find the result of 3′, we need to divide n (which is 21) by 3.
21 divided by 3 equals 7.
The result of 3′ is 7.
To know more about Positive Integer, visit
https://brainly.com/question/29544326
#SPJ11
Benjamín made 3 times more than Alberto and Carlota 2 times more than Benjamín, so how much is it, help me
Answers
Step-by-step explanation:
you are "hiding" some more information (like how much they made together).
without that we cannot calculate the actual values.
all I can do is set up the equations expressing the given relations between the parts of the total :
a = amount Alberto made
b = amount Benjamin made
c = amount Carlota made
b = 3×a
c = 2×b = 2× 3×a = 6×a
that's it.
your see ? now we need something that "ties" all 3 together, an equation of all 3 variables, where we can use the first 2 equations (by substitution) and then solve for the remaining third variable.
and that is missing.
if it is something like "together they made x", then we would have
a + b + c = x
a + 3a + 6a = x
10a = x
a = x/10
b and c we get then from the first 2 equations by simply using the calculated value of a :
b = 3×(x/10) = 3x/10
c = 6×(x/10) = 6x/10 = 3x/5
زFind all the second order partial derivatives of the given function. f(x, y) = e X/y Oht exly 21 ar2 v2 ex/x². + 2xy ) At ava RE acar exlyly 02 13 13 ex/ y21 x2 + 2xy II exy! 11 21 ayak 21 acar v2 02
Answers
The second order partial derivatives of the given function is ∂²f/∂x∂y = ∂/∂y (∂f/∂x) = [(2y - x^2 - 2xy)(-x + 2xy - y^2) + (x^2 + 2xy - y^2)(4xy + y^4 - 2x^2y)]/(x^2 + 2xy + y^2)^4 * e^(x/y)
To find the second-order partial derivatives of the function f(x,y), we first need to find the first-order partial derivatives:
∂f/∂x = (2y - x^2 - 2xy)/(x^2 + 2xy + y^2)^2 * e^(x/y)
∂f/∂y = (-x + 2xy - y^2)/(x^2 + 2xy + y^2)^2 * e^(x/y)
Now, we can find the second-order partial derivatives by taking the partial derivatives of the first-order partial derivatives:
∂²f/∂x² = ∂/∂x (∂f/∂x) = [(2y - x^2 - 2xy)(4xy + y^4 - 2x^2y) - 2(2x + 2y)(x^2 + 2xy + y^2)^2]/(x^2 + 2xy + y^2)^4 * e^(x/y)
∂²f/∂y² = ∂/∂y (∂f/∂y) = [(-x + 2xy - y^2)(-4xy - x^4 + 2xy^2) - 2(-x - 2y)(x^2 + 2xy + y^2)^2]/(x^2 + 2xy + y^2)^4 * e^(x/y)
∂²f/∂x∂y = ∂/∂y (∂f/∂x) = [(2y - x^2 - 2xy)(-x + 2xy - y^2) + (x^2 + 2xy - y^2)(4xy + y^4 - 2x^2y)]/(x^2 + 2xy + y^2)^4 * e^(x/y)
Note that the second-order partial derivatives are very long and complicated expressions involving exponential and polynomial functions of x and y.
To learn more about partial derivatives visit: https://brainly.com/question/30365299
#SPJ11
1. Sally is cleaning houses. She can clean 2/5
of a house in 1/3 of an hour. How much of a
house can she clean in 1 hour?
Answers
Answer:
Step-by-step explanation:
Sally will clean in one hour
2/5*3=6/5=1 1/5 houses in one hour
PLZ ANSWER (6 x 10 ^-7) + ( 6 x 10 ^ -5) in standard form
Answers
give the possible lengths of the legs of a right triangle with a hypotenuse of the square root of 265
Answers
To find the possible lengths of the legs of a right triangle with a hypotenuse of √265, solve the equation a^2 + b^2 = 265 for positive integer pairs (a, b).
To determine the possible lengths of the legs (a, b) of a right triangle with a hypotenuse of √265, we apply the Pythagorean theorem, which states that a^2 + b^2 = c^2, where c represents the hypotenuse. In this case, we have a^2 + b^2 = 265.
To find valid solutions, we search for positive integer pairs (a, b) that satisfy this equation. By trying different values of a and solving for b using the equation, we can identify potential combinations of leg lengths.
It is important to note that there may be multiple valid solutions, as there are various pairs of positive integers that fulfill the Pythagorean theorem for this specific hypotenuse length.
Learn more about Pythagorean theorem click here :brainly.com/question/14930619
#SPJ11
simplify(1-√3)(1/3+√3) leaving your answer in the form p +q √3
Answers
Answer:
-8/3 + 2/3 (√3)
Where, p = -8/3
q = 2/3
Step-by-step explanation:
Simplify(1-√3)(1/3+√3)
= (1-√3)(1/3+√3)
Expand the bracket
= 1(1/3+√3) -√3(1/3+√3)
= 1/3 + √3 - √3/3 - 3
Collect like terms
= 1/3 - 3 + √3 - √3/3
= (1/3 - 3) + (√3 - √3/3)
= -8/3 + [(3√3 - √3)/3]
= -8/3 + 2√3/3
= -8/3 + 1/3( 2√3)
= -8/3 + 2/3 (√3)
Where, p = -8/3
q = 2/3
If z=4-2i, find |z| , |2z| and |3z|. Then investigate if |2z|= 2|z|
Answers
|z|= 2 √(5), |2z|=4 √(5) and |3z|=6 √(5). |2z|= 2|z| this relationship holds true.
Describe Modulus?In mathematics, the modulus, also known as the absolute value or magnitude, is a function that returns the positive value of a number regardless of its sign. The modulus function is denoted by the vertical bars surrounding the number or expression, for example, |x| or |a-b|.
The modulus of a number is defined as the distance of that number from zero on the number line. For example, the modulus of 5 is 5, while the modulus of -5 is also 5. This is because both 5 and -5 are located at a distance of 5 units from zero on the number line.
The modulus function can also be used to express the distance between two numbers. For example, the modulus of the difference between two numbers a and b is written as |a-b|. This gives the distance between the two numbers on the number line, regardless of their signs.
We are given that z = 4 - 2i.
The magnitude (absolute value) of a complex number a + bi is given by |a + bi| = √(a² + b²).
Therefore, we have:
|z| = |4 - 2i| = √(4² + (-2)²) = √20) = 2 √(5)
To find |2z| and |3z|, we multiply z by 2 and 3, respectively, and then take the magnitude:
|2z| = |2(4 - 2i)| = |8 - 4i| = √(8² + (-4)²) = √(80) = 4 √(5)
|3z| = |3(4 - 2i)| = |12 - 6i| = √(12² + (-6)²) = √(180) = 6 √(5)
Finally, we can investigate if |2z| = 2|z|:
|2z| = 4 √(5)
2|z| = 2(2 √(5)) = 4 √(5)
Since |2z| = 2|z|, this relationship holds true.
To know more about function visit:
https://brainly.com/question/23712366
#SPJ1
SIMPLIFYING ALGEBRAIC EXPRESSIONS
-8(9x+7r) use r = -5 and x = 8
Answers
Answer:
-296
Step-by-step explanation:
Answer:
-296
Step-by-step explanation:
-8(9×8+7×-5)
-8 (72 + -35)
-8(37)
-296
if sin(x) = 1 3 and sec(y) = 5 4 , where x and y lie between 0 and 2 , evaluate the expression. cos(2y)
Answers
if sin(x) = 1 3 and sec(y) = 5 4 , where x and y lie between 0 and 2 , then cos(2y) is 17/25.
To evaluate the expression cos(2y), we need to find the value of y and then substitute it into the expression. Given that sec(y) = 5/4, we can use the identity sec^2(y) = 1 + tan^2(y) to find tan(y).
sec^2(y) = 1 + tan^2(y)
(5/4)^2 = 1 + tan^2(y)
25/16 = 1 + tan^2(y)
tan^2(y) = 25/16 - 1
tan^2(y) = 9/16
Taking the square root of both sides, we get:
tan(y) = ±√(9/16)
tan(y) = ±3/4
Since y lies between 0 and 2, we can determine the value of y based on the quadrant in which sec(y) = 5/4 is positive. In the first quadrant, both sine and cosine are positive, so we take the positive value of tan(y):
tan(y) = 3/4
Using the Pythagorean identity tan^2(y) = sin^2(y) / cos^2(y), we can solve for cos(y):
(3/4)^2 = sin^2(y) / cos^2(y)
9/16 = sin^2(y) / cos^2(y)
9cos^2(y) = 16sin^2(y)
9cos^2(y) = 16(1 - cos^2(y))
9cos^2(y) = 16 - 16cos^2(y)
25cos^2(y) = 16
cos^2(y) = 16/25
cos(y) = ±4/5
Since x lies between 0 and 2, we can determine the value of x based on the quadrant in which sin(x) = 1/3 is positive. In the first quadrant, both sine and cosine are positive, so we take the positive value of cos(x):
cos(x) = 4/5
Now, to evaluate cos(2y), we substitute the value of cos(y) into the double-angle formula:
cos(2y) = cos^2(y) - sin^2(y)
cos(2y) = (4/5)^2 - (1/3)^2
cos(2y) = 16/25 - 1/9
cos(2y) = (144 - 25)/225
cos(2y) = 119/225
cos(2y) = 17/25
Therefore, the value of cos(2y) is 17/25.
You can learn more about quadrant at
https://brainly.com/question/28587485
#SPJ11
Find the slope of the line that passes through the following points E (4, 1 2/3) and F (-2,2/3)
Answers
Answer:
1/6
Step-by-step explanation:
To find the slope, we use the slope formula
m = ( y2-y1)/(x2-x1)
m = ( 2/3 - 1 2/3)/(-2 -4)
= -1/-6
= 1/6
rob spent the day at the mall. First, he brought five rabbits for $10 each. Later, he returned two rabbits . After that, he found two twenty dollars bills.Also,he brought two desks two desks for $30 each. write the total change to Rob's funds as an integer
Answers
The requried total change to Rob's funds as an integer is -$50, indicating that he spent more than he received and his funds decreased by $50.
Let's break down the different transactions and calculate the total change to Rob's funds:
Bought 5 rabbits for $10 each: 5 x $10 = $50 spent
Returned 2 rabbits: 2 x $10 = $20 received
Found 2 twenty dollars bills: 2 x $20 = $40 received
Bought 2 desks for $30 each: 2 x $30 = $60 spent
To calculate the total change to Rob's funds, we can add up the amounts received and subtract the amounts spent:
$20 + $40 - $50 - $60 = $-50
Therefore, the total change to Rob's funds as an integer is -$50, indicating that he spent more than he received and his funds decreased by $50.
Learn more about integers here:
https://brainly.com/question/15276410
#SPJ1
3k^2+12k-7kn-28n square meters and a length of 3k-7n meters.
What expression represents the width of the rectangle?
Answers
Step-by-step explanation:
here ! I used the formula area = length × width
and just some algrbric expressions solving

help asap please
question is below

Answers
Step-by-step explanation:
only the second one fulfills the rule that every value of x must have exactly 1 assigned result value (y).
the first option has two different result values (3 and 5) for x = 1.
the third has 2 different result values (3 and 4) for x = 2.
the fourth has 2 different result values (2 and 4) for x = 2, and also 2 different result values (0 and 2) for x = 0.
A countertop is 13 feet long and 2 feet wide.
What is the area of the countertop in square meters? Use the conversion 1 foot = 0.305 meter. Round your final answer to 2 decimal places.
Answers
Answer:
A = 2.42 sq. meters
Step-by-step explanation:
13 feet = 13 × 0.305 = 3.965 meter
2 feet = 2 × 0.305 = 0.61 meter
A = lw
A = (3.965) × (0.61)
A = 2.41865 sq. meters
A = 2.42 sq. meters
Sameera height is 110cm and is gaining 4cm pounds each month sara height is 140cm and is gaining 2cm each month how many months h will it take for sameera to weigh the same as sara
Answers
It would take some time due to their initial height difference and the rates at which they gain weight. Sameera starts at a height of 110cm and gains 4cm per month, while Sara begins at 140cm and gains 2cm per month.
Initially, Sameera is 30cm shorter than Sara. In terms of height gain, Sameera is closing the gap by 2cm each month (4cm - 2cm = 2cm). To reach the same height as Sara, Sameera needs to close the 30cm difference, which will take her 30cm / 2cm = 15 months.
Now, let's consider their weight gain. We don't have specific information about their current weights or weight gain rates, so we can't provide an exact answer in terms of weight. However, if we assume their weight gain rates are proportional to their height gain rates, then it would take Sameera the same 15 months to weigh the same as Sara.
In conclusion, assuming the weight gain rates are proportional to the height gain rates, Sameera would need approximately 15 months to catch up with Sara's weight. It's important to note that this calculation is based on the information provided, and if there are additional factors or variations in their weight gain, the actual time required may differ.
Learn more about Height:
brainly.com/question/29131380
#SPJ11