8 months is – percent of 2 years
Answers
Answer:
33.33%
Step-by-step explanation:
since there are 12 months in a year, that means there are 24 months in 2 years
8/24 = 1/3
Just multiply a fraction by 100% to convert it to percentage form.
100*1/3
33.33%
to check if correct
33.33% × 24 = 7.9992 or 8
7.9992 rounded to the nearest whole number is 8
Related Questions
Part a
determine the area, in square feet, of one triangular face of the square pyramid. show your work or explain your answer.
part b:
determine the total surface area, in square feet, of the square pyramid. show your work or explain your answer.
Answers
A. The Area of one triangular face would be 320 ft². B. The total surface area, in square feet, of the square pyramid is 2,304 ft².
What is the area of the triangle?The Area of one triangular face can be calculated as;
A = area of triangle = ½ x b x h
Where,
b = 32 ft
h = 20 ft
A = ½ x 32 x 20 = 16 x 20
A = 320 ft²
Area of 1 triangular face = 320 ft²
B.
Total surface area = area of the 4 triangular faces + area of the base of the square pyramid
T.S.A = 4(320) + (s²)
Where,
s = 32 ft
T.S.A = 4(320) + (32²)
T.S.A = 1,280 + 1,024
= 2,304 ft²
A. The Area of one triangular face would be 320 ft². B. The total surface area, in square feet, of the square pyramid is 2,304 ft².
Learn more about pyramids here:
https://brainly.com/question/22213308
#SPJ1

Walmart has cashews that sell for $2 a pound and peanuts that sell for $1.50 a pound. Meijer sells cashews for
$2.50 a pound and peanuts for $1 a pound. Mike paid $26 at Walmart and Jim paid $29 at Meijer for the same
amount of nuts. How many pounds of cashews and peanuts did they buy?
Answers
Let "c" represent the amount of cashews they each bought.
Let "p" represent the amount of peanuts they each bought.
Mike: 2c + 1.5p = 26
Jim: 2.5c + 1 p = 29
That's the system you need to solve. We can do this with substitution.
Start with Jim:
2.5c + p = 29
p = 29 - 2.5c
Substitute that into Mike and solve for c:
2c + 1.5p = 26
2c + 1.5(29 - 2.5c) = 26
2c + 43.5 - 3.75c = 26
-1.75c + 43.5 = 26
-1.75c = - 17.5
c = 10
Now substitute that back into Jim's last equation:
p = 29 - 2.5c
p = 29 - 2.5(10)
p = 29 - 25
p = 4
So they each bought 10 pounds of cashews and 4 pounds of peanuts.
can someone please help me quickly??

Answers
Answer:
i think your answer would be 35
Step-by-step explanation:
oh sorry it's answer is 42.
calculate by adding all the individuals less than 40
Sally Sue has money she wants to give away. She has $6400 at month 3 and $5600 at month 7. How much money will she have at month 16?

Answers
HELP HELP HELP HELP HELP

Answers
II. Find the solution set of the following quadratic equations by
factoring:
x^2 - 8x - 9 = 0
100x^2 - 20x = 0
2x^2 - 7x - 15 = 0
x^2 +9x +13 = - 5x-20
3x^2 - 12x + 5 = 9 - 4x^2
Answers
Answer:
see explanation
Step-by-step explanation:
x² - 8x - 9 = 0 ← in standard form
(x - 9)(x + 1) = 0 ← in factored form
Equate each factor to zero and solve for x
x - 9 = 0 ⇒ x = 9
x + 1 = 0 ⇒ x = - 1
-------------------------------------------------
100x² - 20x = 0 ( divide through by 20 )
5x² - x = 0 ( factor out x from each term )
x(5x - 1) = 0
x = 0
5x - 1 = 0 ⇒ 5x = 1 ⇒ x = \(\frac{1}{5}\)
------------------------------------------------
2x² - 7x - 15 = 0 ← in standard form
(2x + 3)(x - 5) = 0 ← in factored form
Equate each factor to zero and solve for x
2x + 3 = 0 ⇒ 2x = - 3 ⇒ x = - \(\frac{3}{2}\)
x - 5 = 0 ⇒ x = 5
---------------------------------------------------------
x² + 9x + 13 = - 5x - 20 (add 5x + 20 to both sides )
x² + 14x + 33 = 0 ← in standard form
(x + 11)(x + 3) = 0 ← in factored form
Equate each factor to zero and solve for x
x + 11 = 0 ⇒ x = - 11
x + 3 = 0 ⇒ x = - 3
-----------------------------------------------------------
3x² - 12x + 5 = 9 - 4x² ( subtract 9 - 4x² from both sides )
7x² - 12x - 4 = 0 ← in standard form
(7x + 2)(x - 2) = 0 ← in factored form
Equate each factor to zero and solve for x
7x + 2 = 0 ⇒ 7x = - 2 ⇒ x = - \(\frac{2}{7}\)
x - 2 = 0 ⇒ x = 2
Solution set of the given quadratic equations are
1. x = 9 or x = -1
2. x=0 or x = 1 / 5
3. x= 5 or x = -3/2
4. x= -11 or x= -3
5. x= 2 or x= -2/7
What is quadratic equation?
" Quadratic equation is an algebraic expression in which highest degree of the given variable is 2."
Formula used
x² +ax + b = (x + c)(x + d)
Where 'a' is the sum 'c' and 'd'
and 'b' is the product of 'c' and 'd'
According to the question,
Factorize all the given quadratic equations we get,
1. x² - 8x - 9 =0
Split middle term of quadratic equation using formula we get,
x² - 9x + x -9 =0
⇒ x(x-9) +1(x - 9) =0
⇒(x -9)(x +1) =0
⇒ x- 9 =0 or x + 1 =0
⇒ x= 9 or x =-1
2. 100x² -20x =0
⇒20x( 5x -1) =0
⇒ 20 ≠ 0, x=0 or 5x - 1=0
⇒ x =0 or x = 1/5
3. 2x² -7x -15 =0
Split middle term of quadratic equation using formula we get,
2x² -10x + 3x -15 =0
⇒ 2x(x-5) +3(x-5)=0
⇒(2x+3)(x-5)=0
⇒2x+3 =0 or x-5 =0
⇒ x= -3/2 or x=5
4. x² +9x +13 = -5x -20
⇒x² +9x + 5x+13 + 20 = 0
⇒x² +14x +33 =0
Split middle term of quadratic equation using formula we get,
x² +11x +3x+33 =0
⇒x(x+11) +3(x+11) =0
⇒(x+3)(x+11) =0
⇒ x= -3 or x=-11
5. 3x² -12x +5 = 9- 4x²
⇒3x²+4x² -12x +5 -9 =0
⇒7x² -12x -4=0
Split middle term of quadratic equation using formula we get,
⇒7x² -14x +2x -4 =0
⇒7x(x-2) +2(x-2)=0
⇒(7x+2)(x-2)=0
⇒7x+2 =0 or x-2 =0
⇒x = -2/7 or x=2
Hence, the solution set of the given quadratic equations are
1. x = 9 or x = -1
2. x=0 or x = 1 / 5
3. x= 5 or x = -3/2
4. x= -11 or x= -3
5. x= 2 or x= -2/7
Learn more about quadratic equation here
https://brainly.com/question/2263981
#SPJ2
Suppose that we are interested in dissolved metals in two Montana streams. In Jack Creek the distribution of dissolved metals is believed to be normal with a mean of 1000 and a standard deviation of 40. For the Cataract Creek the distribution is normal with a mean of 970 and a standard deviation of 20. Random samples of sizes 30 and 15 are taken from Jack and Cataract Creeks respectively. A) Find the mean and variance of the difference in sample means. B) What is the probability that average amount of dissolved metals at Jack Creek is at least 50 more than the average amount of dissolved metals at Cataract Creek?
Answers
The mean of the difference in sample means is 30 and the variance of the difference in sample means is 533.33. The probability that the average amount of dissolved metals at Jack Creek is at least 50 more than the average amount of dissolved metals at Cataract Creek is approximately 8.5%.
A) To find the mean and variance of the difference in sample means, we can use the following formula:
Mean of the difference in sample means = mean of Jack Creek sample - mean of Cataract Creek sample
= 1000 - 970
= 30
The variance of the difference in sample means = (variance of Jack Creek sample/sample size of Jack Creek) + (variance of Cataract Creek sample/sample size of Cataract Creek)
\(\frac{40^2}{30} + \frac{20^2}{15}\)
= 533.33
Therefore, the mean of the difference in sample means is 30 and the variance of the difference in sample means is 533.33.
B) To find the probability that the average amount of dissolved metals at Jack Creek is at least 50 more than the average amount of dissolved metals at Cataract Creek, we need to find the probability that the difference in sample means is at least 50.
We can standardize the difference in sample means using the formula:
\(Z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\)
Where X is the sample mean, μ is the population mean, σ is the population standard deviation, and n is the sample size.
Using the given values, we can calculate the standard error of the difference in sample means:
\(SE = \sqrt{\frac{40^2}{30} + \frac{20^2}{15}}\)
= 14.55
Then, we can calculate the Z-score:
Z = (50 - 30) / 14.55
= 1.38
Using a standard normal table, we find that the probability of a Z-score being greater than 1.38 is 0.0847. Therefore, the probability that the average amount of dissolved metals at Jack Creek is at least 50 more than the average amount of dissolved metals at Cataract Creek is 0.0847, or approximately 8.5%.
To learn more about probability
https://brainly.com/question/30034780
#SPJ4
Please help I need some guidance.
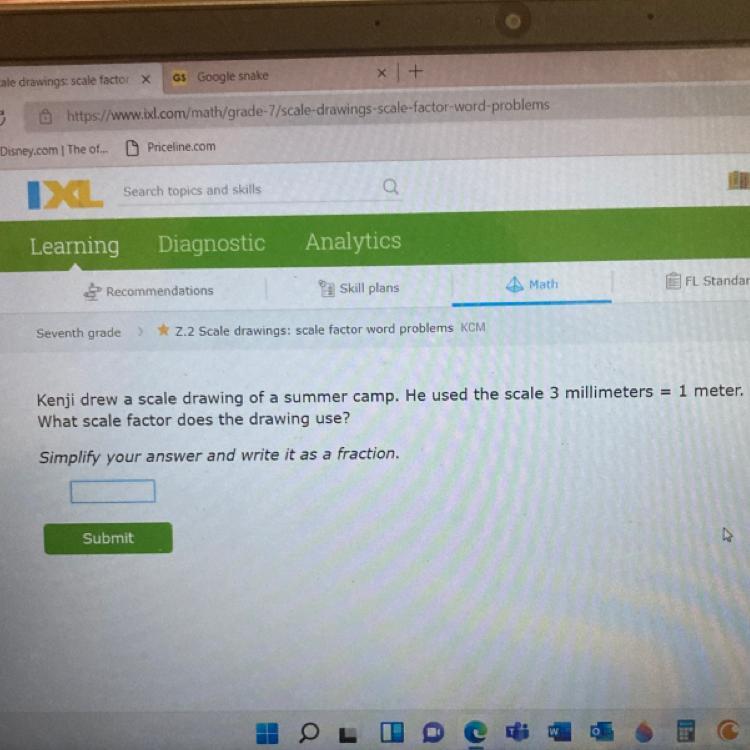
Answers
Answer:
1/333 is answer........
Answer:
3/1000
Step-by-step explanation:
3 millimeters = 0.003 meters
So to get to 1 meter from 3 millimeters, you will have to divide by 0.003 or 3/1000 therefore the scale factor is 3/1000
Form a third-degree polynomial function with real coefficients such that 6 plus i and 7 are zeros
Answers
the third-degree polynomial function with real coefficients, having the zeros 6 + i, 6 - i, and 7, is:
f(x) = (x² - 12x + 37)(x - 7)
To form a third-degree polynomial function with real coefficients such that the complex number 6 + i and the real number 7 are zeros, we can use the fact that complex zeros come in conjugate pairs.
Given that 6 + i is a zero, its conjugate 6 - i will also be a zero. Thus, the zeros of the polynomial are 6 + i, 6 - i, and 7.
To find the polynomial function, we start by forming the factors corresponding to each zero:
(x - (6 + i)) --> This corresponds to the zero 6 + i
(x - (6 - i)) --> This corresponds to the zero 6 - i
(x - 7) --> This corresponds to the zero 7
To simplify the factors, we multiply them out:
(x - (6 + i))(x - (6 - i))(x - 7)
= ((x - 6) - i)((x - 6) + i)(x - 7)
= ((x - 6)² - i²)(x - 7)
= ((x - 6)² + 1)(x - 7)
Expanding the squared term:
= (x² - 12x + 36 + 1)(x - 7)
= (x² - 12x + 37)(x - 7)
Therefore, the third-degree polynomial function with real coefficients, having the zeros 6 + i, 6 - i, and 7, is:
f(x) = (x² - 12x + 37)(x - 7)
Learn more about polynomial function here
https://brainly.com/question/1550346
#SPJ4
The table shows the balance (in dollars) of a bank account each month for three months. What is the average balance of the account?
Month
1$1375.27
2$953.86
3 $1047.79
Answers
The average balance in the bank account is $1,125.64.
What is average?In plain English, an average is a single number chosen to represent a group of numbers; it is typically the sum of the numbers divided by the number of numbers in the group. The average of the numbers 2, 3, 4, 7, and 9 is, for instance, 5. Average The arithmetic mean is calculated by adding a set of numbers, dividing by their count, and then taking the result. For instance, the result of 30 divided by 6 is 5, which is the average of 2, 3, 3, 5, 7, and 10.So, the average balance of the account will be:
Average formula: A = sum of terms/Number of termsFill in the values and solve as follows:
A = sum of terms/Number of termsA = 1375.27 + 953.86 + 1047.79/3A = 1375.27 + 953.86 + 1047.79/3A = 3,376.92/3A = $1,125.64Therefore, the average balance in the bank account is $1,125.64.
Know more about average here:
https://brainly.com/question/20118982
#SPJ13
Can someone help me with this please?

Answers
Answer:
Tall = 32.9 in
Step-by-step explanation:
Pythagorean theorem:
diagonal² = width² + tall²
59² = 49² + tall²
3481 = 2401 + tall²
3481 - 2401 = tall²
1080 = tall²
√1080 = √tall²
tall = 32.863 in
The nearest thent is:
32.9 in
Simplify each rational expression. State any restrictions on the variable. x²+10 x+25 / x²+9 x+20
Answers
The rational expression (x² + 10x + 25) / (x² + 9x + 20) simplifies to (x + 5) / (x + 4), with the restriction that x cannot be equal to -4.
To simplify the rational expression (x² + 10x + 25) / (x² + 9x + 20), we can factorize the numerator and denominator and then cancel out any common factors.
Factorizing the numerator:
x² + 10x + 25 = (x + 5)(x + 5) = (x + 5)²
Factorizing the denominator:
x² + 9x + 20 = (x + 4)(x + 5)
Now, we can simplify the expression:
(x² + 10x + 25) / (x² + 9x + 20) = (x + 5)² / (x + 4)(x + 5)
After canceling out the common factor (x + 5) from the numerator and denominator, we are left with:
= (x + 5) / (x + 4)
Therefore, the simplified rational expression is (x + 5) / (x + 4). However, we need to note the restriction on the variable. In this case, x cannot be equal to -4 since it would result in division by zero, which is undefined. So, the restriction is x ≠ -4.
To learn more about expression Click Here: brainly.com/question/28170201
#SPJ11
You inherit RM300,000 from your parents and want to use the money to supplement your retirement. You receive the money on your 65 th birthday, the day you retire. You want to withdraw equal amounts at the end of each of the next 20 years. What constant amount can you withdraw each year and have nothing remaining at the end of 20 years if you are earning 7% interest per year?
A. RM15,000
B. RM28,318
C. RM33,574
D. RM39,113
Answers
To determine the constant amount that can be withdrawn each year for 20 years, we need to calculate the annuity payment using the present value of an annuity formula.
Inherited amount: RM300,000
Interest rate: 7% per year
Number of years: 20
Using the present value of an annuity formula:
PV = P * [(1 - (1 + r)^(-n)) / r]
Where:
PV = Present value (inherited amount)
P = Annuity payment (constant amount to be withdrawn each year)
r = Interest rate per period (7% or 0.07)
n = Number of periods (20 years)
Plugging in the values:
300,000 = P * [(1 - (1 + 0.07)^(-20)) / 0.07]
Solving this equation, we find that the constant amount that can be withdrawn each year is approximately RM15,000.
Therefore, the correct answer is A. RM15,000.
To know more about interest click here: brainly.com/question/30393144
#SPJ11
3 The The curve y=ax² +bac + 5 where a and b are constants has a turning point p (1,3). find the values of a and b and determine whether P is a maximum or a minimum point,
Answers
Answer:
a = 2, b = -2
P is at a minimum
Step-by-step explanation:
For any polynomial function, the turning point is either a maximum or a minimum
It can be determined by taking the first derivative of the function and setting it equal to 0 and solving for x and y
In this case we are given the turning point as x=1, y = 3 and we have to calculate a and b in the equation y = ax² + (ab)x + 5
The first derivative of y, y' = 2ax + ab
If we set this equal to 0 we get 2ax + ab = 0 ==> 2ax = -ab ==> b = -2
So the equation is of the form y = ax² -2ax + 5 (subbing for b)
Since we know that at x = 1, y =3 substitute y and x values in the above equation and solve for a
y = 3 = a(1²) - 2a(1) + 5
a - 2a + 5 = 3
-a + 5 = 3
a = 2
So the equation is of the form y = 2x² -4x + 5
If we plot this we will find that P is a minimum point
However, we can always determine mathematically if P is a max or min by taking the second derivative of the original function and noting the sign. If it is positive, the point is a minimum, and if it is negative, the point is a maximum.
Taking derivatives,
y' = 4x - 4
y'' = (4x-4)' = 4
The sign is positive so P is a minimum
Graph attached for reference

A retailer marks up the price of a coffee mug from $6.25 to $8.77. By what percent did the price increase? Round to two decimal places. a. 28.73% b. 39.68% c. 40.32% d. 45.97%
Answers
Answer:
c. 40.32%
Step-by-step explanation:
8.77-6.25 = 2.52
2.52/6.25 x 100 = 40.32%
Hope this helps!
Answer:
c. 40.32%
Step-by-step explanation:
Read the poem "Jerusalem" by William Blake, and then answer the questions that follow. Jerusalem And did those feet in ancient time Walk upon England’s mountain green? And was the holy Lamb of God On England’s pleasant pastures seen? And did the Countenance Divine Shine forth upon our clouded hills? And was Jerusalem builded here Among these dark Satanic mills? Bring me my bow of burning gold! Bring me my arrows of desire! Bring me my spear! O clouds, unfold! Bring me my chariot fire. I will not cease from mental fight, Nor shall my sword sleep in my hand ‘Til we have built Jerusalem In England’s green and pleasant land. In the fourth stanza, what course of action does he propose?
Answers
In the fourth stanza, William Blake proposes the course of action of not ceasing from the mental fight and not letting his sword sleep in his hand until they have built Jerusalem in England’s green and pleasant land.
The stanza from the poem "Jerusalem" by William Blake is given below:"Bring me my bow of burning gold!Bring me my arrows of desire!Bring me my spear!O clouds, unfold!Bring me my chariot fire.I will not cease from mental fight,Nor shall my sword sleep in my hand‘Til we have built Jerusalem In England’s green and pleasant land."Explanation:The poem "Jerusalem" is a poem by William Blake that was published in his book Milton: a Poem in 1804. It is the preface poem of the work, which is a long poem consisting of 12 books. The poem is inspired by the legend of the young Jesus Christ who is said to have visited England during his early life. It is a hymn of English nationalism and uses the image of Jerusalem as a metaphor for a new and better society.Blake's Jerusalem is not just a physical place but a metaphorical one as well. The poem urges people to strive for a better, more just society. He uses his imagery of building Jerusalem to convey his message. Blake's use of the phrase "mental fight" suggests that this is not a physical battle but a battle of the mind. Blake believes that people must not give up the fight and must continue to fight for a better society. Therefore, in the fourth stanza of the poem "Jerusalem," Blake proposes the course of action of not ceasing from the mental fight and not letting his sword sleep in his hand until they have built Jerusalem in England’s green and pleasant land.
To know more about William Blake visit:
https://brainly.com/question/30553667
#SPJ11
What is the equation of a line passing through the point (-4, 8) that is parallel to the line y = 2x + 6

Answers
Answer:
y = 2x + 16
Step-by-step explanation:
slope is parallel and equal to y = 2x + 6
y intercept = 16
Answer:
b - y=2x+16
Step-by-step explanation:
y=y1+m(x+x1)
(-4,8)
y=8+2(x-4)
y=8+2x-8
add 8 on both sides
y=2x+16
Consider the figure below. Which statement is most correct about the triangles?
a). ΔTRP~ΔTSG by SAS~
b). ΔTRP~ΔTSG by SSS~
c). ΔTRP~ΔTSG by AA~
d.) Similarity cannot be concluded with the information given

Answers
ΔTRP~ΔTSG by AA~
============================================
Further Explanation:
Triangles TRP and TSG share an overlapping angle at point T. This is one pair of congruent angles.
Due to the parallel lines (PR and GS), we can get two more pairs of congruent angles:
angle TSG = angle TRPangle TGS = angle TPRThese congruences are valid because of the corresponding angle theorem.
You could use all three, but at minimum, you only need 2 pairs of congruent angles. Once we have two pairs of congruent angles, we can use the AA (angle angle) similarity theorem. Your teacher has abbreviated this as AA~
We cannot use SAS and SSS because we don't have any information about the sides.
Four golfers will be randomly split into 2 groups of 2 for a tournament: If Jill and Ramona are among the 4. what is the probability that they will be paired together? F # G. H: 8 J: 4 K 3
Answers
The probability that Jill and Ramona will be paired together is given as follows:
1/4.
How to calculate a probability?The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is then calculated as the division of the number of desired outcomes by the number of total outcomes.
The total number of pairs for this problem is given as follows:
2² = 4.
Jill and Ramona form one pair, hence the probability is given as follows:
p = 1/4.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1
Find the value of x that makes the following equation true
- 4x + 26 = -2
Answers
Answer:
first collect the like terms so that you have -4x is equals to -2 - 26 then negative 4x is equals to -28 divided by -4x is equals to 7
im on a donating mission! Today im going to donate 100 food items to the local food bank
Answers
Brian Chris and Damien took a math test that had 20 questions. The number of questions Brian got right is 14 more than the number of
questions Chris got right. Damien correctly answered 2 less than 4 the number of questions Chris answered correctly.
It Brian and Darmente
the same score, which statement is true?
OA Brian and Damien both answered 2 fewer questions correctly than Chris did.
OB Brian and Damien both answered 4 more questions correctly than chris did.
OcBrian and Damien both answered 2 more questions correctly than Chris did.
OD. Brian and Damien both answered 4 fewer questions correctly than Chris did.
Reset
Next
Answers
Answer:
C.) they both got two more questions correctly than Chris did.
Step-by-step explanation:
brian got 14 more right than chris
Chris got 2 less than damien
brian and damien both got 18/20 correct, chris got 16 right
PLEASE HELP I WILL MAR YOU BRAINLIEST

Answers
Answer:
C
Step-by-step explanation:
Its a reflection then its dilation, however its not congruent because congruent means that its the same size and shape in this case its only the same shape not size.
First of all the quadrilateral ABCD is reflected, which means sides are changed and then it is dilated. A dilated image is always similar but never congruent. The meaning of congruency is that both size and shape is equal but here only shape is equal not the size so it is not congruent to the original...
Help again for like the 2nd time

Answers
Answer:
d) 94°
Step-by-step explanation:
supplementary means 'adds up to 180°
86 + m∡3 = 180
m∡3 = 180 - 86
(1 point) find the angle θ between the vectors a=9i−j−5k and b=2i j−8k.
Answers
The required answer is the angle between vectors a and b is 44.8 degrees.
To find the angle θ between two vectors a and b, we use the dot product formula:
a · b = |a| |b| cos θ
where |a| and |b| are the magnitudes of vectors a and b, respectively.
First, let's calculate the dot product of a and b:
a · b = (9)(2) + (-1)(0) + (-5)(-8) = 18 + 40 = 58
Variable were explicit numbers solve a range of problems in a single computation. The quadratic formula solves any quadratic equation by substituting the numeric values of the coefficients of that equation for the variables that represent them in the quadratic formula. A variable is either a symbol representing an unspecified term of the theory , or a basic object of the theory that is manipulated ,without referring to its possible intuitive interpretation.
Next, let's calculate the magnitudes of vectors a and b:
|a| = sqrt(9^2 + (-1)^2 + (-5)^2) = sqrt(107)
|b| = sqrt(2^2 + 1^2 + (-8)^2) = sqrt(69)
the angle θ by taking the inverse cosine of the cosine value: θ = (57 / (√107 * √69)
Now we can substitute these values into the dot product formula to solve for θ:
58 = sqrt(107) sqrt(69) cos θ
cos θ = 58 / (sqrt(107) sqrt(69))
θ = cos^-1(58 / (sqrt(107) sqrt(69)))
Now you have the angle θ between the two vectors a and b.
Using a calculator, we find that θ is approximately 44.8 degrees.
Therefore, the angle between vectors a and b is 44.8 degrees.
To know more about the variable. Click on the link.
https://brainly.com/question/15078630
#SPJ11
Maggie has 7 bills, all tens and twenties, that
total $100 in value. Find the number of tens, x, and
the number of twenties, y, that Maggie has.
Answers
Answer:
4 tens, 3 twenties
Step-by-step explanation:
4 tens ($40) and 3 ($60) twenties work. I’m sorry I don’t have a formula for it though.
x2 + 45x = -200 Using the quadratic formual and the discirimnat
Answers
Answer:
Positive discriminant = 2 real solution
x= -5,-40
Step-by-step explanation:
The discriminant is used to see how many solutions an equation has. If it is negative, the equation has no real solutions, if =0 the equation has 1, and if it is positive, the equation has two real solutions.
The discriminant is the part of the quadratic formula inside the square root:
\(b^{2}-4ac\)
Every quadratic formula has the structure:
\(ax^{2} +bx+c=0\)
So first, in order to meet this structure we need to add 200 to both sides so the equation is equal to 0. This gives us:
\(x^{2} +45x+200=0\)
Our a=1, b=45 and c=200
Now we can substitute these values into the discriminant:
\((45)^{2} -4(1)(200)\)
Solve:
\(2025-800=1225\)
The discriminant is a positive number which means this equation will have 2 real solution. Now we just need to plug in our values into the quadratic formula to solve this equation. Quadratic formula:
\(x=\frac{-+/-\sqrt{b^{2}-4ac} }{2a} \\x=\frac{-45+/-\sqrt{1225} }{2}\)
(Same discriminant value)
\(x=\frac{-45+/-35}{2}\)
Now to find the two solutions, we use both signs in the equation. Solution 1:
\(x=\frac{-45+35}{2}\)
\(x=\frac{-10}{2}=-5\)
Our first solution is -5, now for the second:
\(x=\frac{-45-35}{2}\\\\ x=\frac{-80}{2}=-40\)
The two solution to this equation are -5 and -40.
Hope this helped!
limit as x approaches infinity is the square root of (x^2+1)
Answers
The value of the given function `limit as x approaches infinity is the square root of (x^2+1)` is √(x^2 + 1).
We have to find the value of the limit as x approaches infinity for the given function f(x) = sqrt(x^2 + 1).
Let's use the method of substitution.
Replace x with a very large value of positive integer 'n'.
Now, let's solve for f(n) and f(n+1) to check the behavior of the function.f(n) = sqrt(n^2 + 1)f(n+1) = sqrt((n+1)^2 + 1)f(n+1) - f(n) = sqrt((n+1)^2 + 1) - sqrt(n^2 + 1)
Let's multiply the numerator and denominator by the conjugate and simplify:
f(n+1) - f(n) = ((n+1)^2 + 1) - (n^2 + 1))/ [sqrt((n+1)^2 + 1) + sqrt(n^2 + 1)]f(n+1) - f(n) = (n^2 + 2n + 2 - n^2 - 1)/ [sqrt((n+1)^2 + 1) + sqrt(n^2 + 1)]f(n+1) - f(n) = (2n+1)/ [sqrt((n+1)^2 + 1) + sqrt(n^2 + 1)]
Thus, we can see that as n increases, f(n+1) - f(n) approaches to 0. Therefore, the limit of f(x) as x approaches infinity is √(x^2 + 1).
Therefore, the value of the given function `limit as x approaches infinity is the square root of (x^2+1)` is √(x^2 + 1).
Know more about square root here:
https://brainly.com/question/3617398
#SPJ11
Determine whether the series is convergent or divergent. 1 + 1/16 + 1/81 + 1/256 + 1/625 + ...
the series is _____ p-series with p = _____.
Answers
The given series is convergent. It is a p-series with p = 2 because each term is in the form of 1/n².
The p-series with p > 1 always converge, so this series converges. This means that the sum of the terms in the series approaches a finite value as the number of terms approaches infinity.
In other words, the series does not diverge to infinity or oscillate between positive and negative values. The convergence of this series can be proven using the integral test or by comparing it to another convergent series.
To know more about convergent series click on below link:
https://brainly.com/question/9520631#
#SPJ11
Jorge is looking for a new job after finishing his college degree. He is currently working part time to pay the bills, but is also applying for jobs that match his career plans. Jorge is:
Answers
Jorge is a recent college graduate who is eagerly seeking new job opportunities after completing his degree.
Currently, he is working part-time to cover his expenses, but his true ambition lies in finding a job that aligns with his long-term career plans. In order to achieve this, Jorge has been actively applying to various positions that match his professional aspirations and utilize the knowledge and skills he acquired during his college education.
Jorge's qualifications can be measured by various factors such as his college degree, GPA, relevant coursework, internships, and any additional certifications he may have obtained. These factors contribute to his overall level of qualification, denoted as x.
Mathematically, we can express this as:
C(x) ≥ D(x)
This inequality indicates that Jorge's qualifications need to meet or surpass the demands of the job market for him to be considered a strong candidate for the career opportunities he desires.
In summary, Jorge's current situation involves a pursuit of a fulfilling career that matches his aspirations.
To know more about career here
https://brainly.com/question/8825832
#SPJ4