8 1/3 % of 64
mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm
Answers
Answer:
I think it is 7.86.
Step-by-step explanation:
You should change 8 1/3% to a decimal that equals 8.33333333333. I then had took 64/8.33333333333 which equaled 7.86.
If this helped please feel free to click the thanks button below. Thank you! :-D
Related Questions
The shaded area below is 79 m².
Work out the area of the smaller rectangle.
If your answer is a decimal, give it to 2 d.p.
x+4 m
x + 3 m
x+2m
2x+5 m
Not drawn accurately

Answers
Answer:
\((x + 4)(2x + 5) - (x + 3)(x + 2) = 79 \\ 2x {}^{2} + 5x + 8x + 20 - {x}^{2} - 2x - 3x - 6 = 79 \\ {x}^{2} + 8x + 14 = 79 \\ {x}^{2} + 8x - 65 = 0 \\ {x}^{2} + 13x - 5x - 65 = 0 \\ x(x + 13) - 5( x + 13) = 0 \\ (x - 5)(x + 13) = 0\)
x-5=0
x=5
the length of smaller rectangle= 8 m
and breadth of s. rectangle= 7 m
l x b = 8 x 7
\(56 {m}^{2} \)
hopefully this will u
the population in a small us city has been increasing linearly. in 2014, the population of this town was 29,333. by the year 2019, it grew to 35,203. the function/model/equations is:
Answers
If the population grew to 35203 by the year 2019 , then the equation to model this situation is y = 1174x + 29333 .
We use the given data points to create a linear equation to model the population growth over the years.
Let , x₁ = 0 represents the year 2014
⇒ y₁ = 29333 represents the population in the year 2014
⇒ x₂ = 5 represents the year 2019
⇒ y₂ = 35203 represents the population in the year 2019
Using these variables, we can find the slope of the line that represents the population growth:
So , slope = (y₂ - y₁)/(x₂ - x₁)
⇒ slope = (35203 - 29333)/(5 - 0) ;
⇒ slope = 5870/5 = 1174 ;
Now , by using the point-slope form of a linear equation
we get ;
⇒ y - y₁ = m(x - x₁) ;
⇒ y - 29333 = 1174(x - 0) ;
Simplifying this equation ;
we get ;
⇒ y = 1174x + 29333 ;
Therefore, the equation for the model is y = 1174x + 29333, where y represents the population and x represents the number of years since 2014.
Learn more about Equation here
https://brainly.com/question/9630347
#SPJ4
The given question is incomplete , the complete question is
The population in a small us city has been increasing linearly. in 2014, the population of this town was 29333. and by the year 2019, it grew to 35,203. Find the equation for this model ?
Please help! Homework!!

Answers
1. The expression that represents the area of the shaded region is π (R² - r²). 2. Yes, the expression is a polynomial with degree 2. 3. The difference is given by the (R - r). It is a polynomial with degree 1.
What is a polynomial?When variables and coefficients are joined using addition, subtraction, and multiplication operations, the result is a polynomial. The coefficients of a polynomial can be any real number, and the variables can only have non-negative integer exponents. Polynomials can have one or more terms, and they can be categorised according to the degree of the variable in the expression with the largest power. For instance, the aforementioned polynomial is of fourth degree since the maximum power of the variable x is 4.
The area of the circle is given as:
A = πr²
For the outer circle the area is:
A1 = πR²
The area of inner circle is:
A2 = πr²
Now, the area of the shaded portion is:
A = A1 - A2
A = πR² - πr²
A = π (R² - r²)
Hence, the expression that represents the area of the shaded region is π (R² - r²).
2. Yes, the expression is a polynomial with degree 2.
3. The difference between the two radii is given by the expression R - r. It is a polynomial with degree 1.
Learn more about polynomial here:
https://brainly.com/question/11536910
#SPJ1
Can you solve for a,b and c
2a - 3b = -5
4a + 3b = 17
50 - 2a = 1
Answers
Answer:
\(a = \frac{49}{2}\)
\(b = 18\)
Step-by-step explanation:
Lets focus on the third equation to find a:
50 - 2a = 1
Add 2a to both sides of the equation:
50 - 2a + 2a = 1 + 2a
50 = 1 + 2a
Subtract 1 from both sides of the equation:
50 - 1 = 1 + 2a - 1
49 = 2a
Divide both sides by 2:
\(\frac{2a}{2} = \frac{49}{2}\)
\(a = \frac{49}{2}\)
Now substitute in the know a variable into the first equation:
\(2a - 3b = -5\)
\(49 - 3b = -5\)
Add 3b to both sides:
\(49 - 3b + 3b = -5 + 3b\\49 = -5 + 3b\)
Add 5 to both sides:
\(49 + 5 = -5 + 3b + 5\)
54 = 3b
Divide both sides by 3:
\(\frac{53}{3} = \frac{3b}{3}\)
\(b = 18\)
c cannot be solved as there is no c variable.
Hope this helps!
let x ~ geometric(1/3), i.e., p(x = k) = (1/3)(1-1/3)^k for k = 0, 1, 2, 3, .... what is the probability that x is odd?
Answers
The probability that x is odd is 3/5 for p(x = k) = (1/3)(1-1/3)^k for k = 0, 1, 2, 3,
In a geometric distribution, the probability of the kth trial being a success is given by p(k) = p(1-p)^(k-1), where p is the probability of success in a single trial. In this case, x is a geometric distribution with p = 1/3.
To find the probability that x is odd, we can sum the probabilities of all odd values of x. That is,
P(x is odd) = P(x=1) + P(x=3) + P(x=5) + ...
Substituting the formula for the geometric distribution, we get
P(x is odd) = (1/3)(1-1/3)^0 + (1/3)(1-1/3)^2 + (1/3)(1-1/3)^4 + ...
Notice that this is an infinite geometric series with first term a = (1/3) and common ratio r = (2/3)^2. The sum of an infinite geometric series is given by a/(1-r), so we have
P(x is odd) = (1/3) / (1 - (2/3)^2) = (1/3) / (5/9) = 3/5.
To learn more about probability click on,
https://brainly.com/question/15081092
#SPJ4
please help its due today


Answers
The measure of the angles are: K, L, C, N, O G = -3/4, 65, 8 40.4, 89 and 44 respectively
How to find the measure of the angles?To determine K
9x + 2 = 23 + 5x -1
9x -5x = -1 +2
4x = -3Making x the subject we have
x= -3/4
To find the value of L
Let angle L be x
x + 65 = 130
x=130-65
That is x = 65
To find the m<C
4x + 7 = 3x + 15
Collecting like terms
4x - 3x = 15-7
Making x the subject of the relation we have
x=8
To find the m<N
7x + 6x - 1 = 90
13x = 89
x=89/13
x= 6.9
Substitute x = 6.9 in 6x -1
6(6.9) -1
m<L = 40.4
To find the m<O
5x - 11 = 4x +9
5x-4x = 9 +11
x=20
By substitution in 4x +9 we have
4(20) +9
80+9
m<S = 89
To find the value of the angle G
6x - 4 = 5x +4
6x - 5x = 4+4
x = 8
Therefore the m<G is
5x +4
5(8) +4
40+4 = 44 digress
Learn more about measure of angles in https://brainly.com/question/28451077
#SPJ1
Conducting numerous, separate statistical analyses increases the chance that one or more of the results appear to be statistically significant, but are actually attributable to random variation or measurement error. The problem is referred to as:
Answers
A family-wise inflation of error rate is the increase in the probability that one or more results of a numerous, independently (separately) conducted statistical analyses to become statistically significant, but these results can actually be attributed to random variation or measurement error.
In Statistics, a family-wise inflation of error rate is also referred to as family-wise error rate (FWER) and it can be defined as the probability of making at least one false conclusion or type I errors in numerous, separate statistical analyses or hypothesis tests.
Hence, a family-wise inflation of error rate increases the probability that one or more of the results among groups within an independent data set to be statistically significant, especially due to random variation or measurement error.
Read more: https://brainly.com/question/22851088
Find the perimeter of the window to the nearest hundredth perimeter: about ft
Answers
Answer:
I would answer but I have no numbers to give the answer
55 points
2. Sammy throws a drawing pin 200 times and records how it lands
Pin up 160
Pin down 40
a. What is the probability the pin will land i) pin up? ii) pin down
b. How many pin ups would you expect if the pin was thrown i) 80 times ii)320 times iii) 400 times iv)1000 times
Answers
Answer:
160:40 or 160 to 40, 80:320 or 80 to 320, 400:1000 or 400 to 1000
Step-by-step explanation:
Free Pls help
Question: Solove for X

Answers
I'm sorry, I thought I could have helped. I hope you have a nice day!
Line AB and line BC form a right angle at point B. If A = (2, 5) and B = (4, 4), what is the equation of line BC?
Answers
Answer:
y = 2x - 4
Step-by-step explanation:
To solve this problem, we must first calculate the slope of the line AB using the formula:
\(\boxed{m = \frac{y_2 - y_1}{x_2 - x_1}}\)
where:
m ⇒ slope of the line
(x₁, y₁), (x₂, y₂) ⇒ coordinates of two points on the line
Therefore, for line AB with points A = (2, 5) and B = (4, 4) :
\(m_{AB} = \frac{5 - 4}{2 - 4}\)
⇒ \(m_{AB} = \frac{1}{-2}\)
⇒ \(m_{AB} = -\frac{1}{2}\)
Next, we have to calculate the slope of the line BC.
We know that the product of the slopes of two perpendicular lines is -1.
Therefore:
\(m_{BC} \times m_{AB} = -1\) [Since BC and AB are at right angles to each other]
⇒ \(m_{BC} \times -\frac{1}{2} = -1\)
⇒ \(m_{BC} = -1 \div -\frac{1}{2}\) [Dividing both sides of the equation by -1/2]
⇒ \(m_{BC} = \bf 2\)
Next, we have to use the following formula to find the equation of line BC:
\(\boxed{y - y_1 = m(x - x_1)}\)
where (x₁, y₁) are the coordinates of a point on the line.
Point B = (4, 4) is on line BC, and its slope is 2. Therefore:
\(y - 4 =2 (x - 4)\)
⇒ \(y - 4 = 2x - 8\) [Distributing 2 into the brackets]
⇒ \(y = 2x-4\)
Therefore, the equation of line BC is y = 2x - 4.
18. If f(x) = arccos(x^2), then f'(x) =
Answers
The derivative of f(x) = arccos(x^2) is: f'(x) = -2x / √(1-x^4)
The derivative of f(x) = arccos(x^2), we'll use the chain rule. The chain rule states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function. In this case, the outer function is arccos(u) and the inner function is u = x^2.
First, let's find the derivative of the outer function, arccos(u). The derivative of arccos(u) is -1/√(1-u^2). Next, we'll find the derivative of the inner function, x^2. The derivative of x^2 is 2x.
Now we'll apply the chain rule. We have:
f'(x) = (derivative of outer function) * (derivative of inner function)
f'(x) = (-1/√(1-u^2)) * (2x)
Since u = x^2, we'll substitute that back into our equation:
f'(x) = (-1/√(1-x^4)) * (2x)
So, the derivative of f(x) = arccos(x^2) is:
f'(x) = -2x / √(1-x^4)
To learn more about Derivative :
https://brainly.com/question/23819325
#SPJ11
If a person consumes a 2500 kcal daily diet, of which 35% is from proteins, the individual would consume approximately grams of protein. (round to the nearest gram)
Answers
Approximately 109 grams of protein would be consumed on a 2500 kcal daily diet, with 35% of the calories coming from proteins.
Protein intake is an important aspect of a healthy diet, as it plays a vital role in various bodily functions. To calculate the grams of protein consumed, we start by determining the total calorie intake and then find the proportion of calories that come from proteins. In this case, the daily diet consists of 2500 kcal. To find the protein calories, we multiply this by the percentage of calories from proteins, which is 35%. This gives us 0.35 * 2500 = 875 kcal from proteins.
Next, we need to convert these calories into grams of protein. Each gram of protein provides approximately 4 calories. Therefore, we divide the protein calories (875 kcal) by 4 to get the grams of protein consumed, which is 875 / 4 ≈ 218.75 grams. Rounding this to the nearest gram, the individual would consume approximately 219 grams of protein on a 2500 kcal daily diet with 35% of the calories coming from proteins.
Learn more about Protein
brainly.com/question/31017225
#SPJ11
The following table provides information about the median income in four states in
2016. Virginia had an index of 127.2 that year. What was the median income in Virginia?
NEED HELP ASAP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
PLEASE SHOW STEP BY STEP EXPLANATION!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
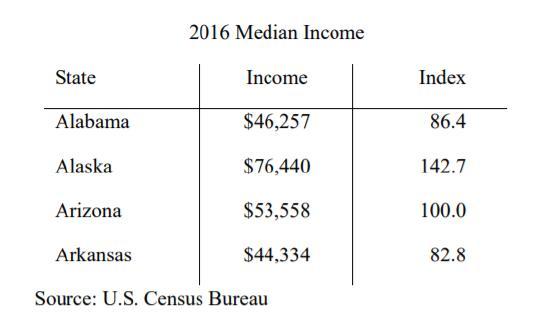
Answers
Answer:
$68,213
Step-by-step explanation:
The median is the middle value number.
So you need median for Virginia.
First lets see how index and income are connected.
To do this divide the income by the index to see if you have a constant value you can use.
535.434783 = Arkansas
535.381944 = Alabama
535.58 = Arizona
535.669236 = Alaska
535 is constant in all of these.
Let's multiply the index by 535.
127.2*535 =68212.5
For median income, you need a whole number so lets round up.
68213
So Virginia would have a median income rate of $68,213
If you have anymore questions, don't be afraid to reach out and I hope that helps!
a cylindrical tank for refrigerant has an inside diameter of 14 inches and is 16 inches high. what is the volume of the tank in cubic inches?
Answers
The volume of the cylindrical tank for refrigerant with an inside diameter of 14 inches and a height of 16 inches is 10,736 cubic inches.
The volume of a cylinder can be calculated using the formula:
\(\[ V = \pi r^2 h \]\)
where V represents the volume, \(\(\pi\)\) is a mathematical constant approximately equal to 3.14159, r is the radius of the cylinder (which is half the diameter), and h is the height of the cylinder.
In this case, the inside diameter of the tank is given as 14 inches, so the radius can be calculated as \(\(r = \frac{14}{2} = 7\)\) inches. The height of the tank is given as 16 inches. Substituting these values into the formula, we get:
\(\[ V = 3.14159 \times 7^2 \times 16 \approx 10,736 \text{ cubic inches} \]\)
Therefore, the volume of the cylindrical tank for refrigerant is approximately 10,736 cubic inches.
To learn more about volume refer:
https://brainly.com/question/28058531
#SPJ11
I hope you can see this well I just need help on this problem.

Answers
Given:
a.) The width of the rectangle is 0.7 meters less than the length.
b.) The perimeter of a rectangle is 44.6 meters.
First, let's draw the rectangle to better understand the problem.
Recall: The formula in getting the perimeter of the rectangle.
\(\text{ Perimeter = 2Length + 2Width}\)But it stated that the width of the rectangle is 0.7 meters less than the length.
Thus,
Width = Length - 0.7
Let's now find its Length,
\(\begin{gathered} \text{ Perimeter = 2Length + 2Width} \\ \text{ 44.6 = 2Length + 2(Length - 0.7)} \\ \text{ 44.6 = 2Length + 2Length - 1.4} \\ \text{ 44.6 + 1.4 = 4Length} \\ \text{ 46 = 4Length} \\ \text{ 4Length = 46} \\ \text{ }\frac{\text{4Length}}{\text{ 4}}\text{ = }\frac{\text{ 46}}{\text{ 4}} \\ \text{ Length = }11.5\text{ meters} \end{gathered}\)Therefore, the length of the rectangle is 11.5 meters.
Let's now determine the width,
Width = Length - 0.7
= 11.5 - 0.7
Width = 10.8 meters
Therefore, the width of the rectangle is 10.8 meters.

a washing machine can hold 3/4 kg of laundry in each load. if randy has . 6 kilograms of laundry, how many loads does he need to do? 5 6 7 d8
Answers
Randy needs 8 loads.
To find the answer on the question we have to follow the method of multiplication and division .
A washing machine can hold \(\frac{3}{4}\) kg of laundry in each load.
\(\frac{3}{4}\) kg of laundry is equal to 1 load.
\(\frac{3}{4}\) kg of laundry = 1 load
1 kg of laundry = \(\frac{1 * 4}{3}\) load ( following the method of division )
1 kg of laundry = \(\frac{4}{3}\) load
Randy has 6kg of laundry.
So, 1kg of laundry i.e \(\frac{4}{3}\) load is to be multiplied by 6.
6kg of laundry = \(\frac{4 * 6}{3}\) load ( following the method of multiplication)
= 8 loads
Hence, Randy needs 8 loads.
Read more about multiplication :
https://brainly.com/question/26669440
#SPJ4
Reflect the function f(x) = x4 about the x-axis and translate it 3 units to the left to produce g(x). Which equation represents the function g(x)?.
Answers
When f(x) = x⁴ is reflected about the x-axis and translated 3 units to left we get y = -(x - 3)⁴.
Therefore, g(x) = -(x - 3)⁴.
When a function, f(x) is reflected about the x-axis, we get y = -f(x). Therefore here when f(x) = x⁴ is reflected about the x-axis we get y = -x⁴.
When a function, f(x) is translated by a units to the left we get y = f(x-a).
Thus here we obtain y = -(x - 3)⁴
To know more on translation of graph
https://brainly.com/question/12951849
#SPJ4
143 inches = ________ a) 14 feet 3 inches b) 13 feet 9 inches c) 12 feet 2 inches d) 11 feet 11 inches
Answers
Answer:
D. 11 feet 11 inches
1 foot= 12 inches
143/ 12 = 11 11/12
Answer:
D) 11 feet and 11 inches
Step-by-step explanation:
First we know that there is 12 inches in a foot. So let's start with a.
14 inches x 12 inches (one foot) is 168 inches (so it's not this one:)
13 inches x 12 inches is 156 inches (It's not this one either)
12 inches x 12 inches is 144 inches (not this one)
11 inches x 12 inches is 132 inches (so it could be this one, let's add the remaining inches).
132 + 11 inches = 143 inches.
(Notice I didn't add the remaining inches on A, B, or C because the number of inches was already too much. I did on D because the number of inches was below the given number of 143.
Hope this helps!!
Have a wonderful day!!
let f be a function with derivative given by f'(x)=x^3-8x^2 3/
Answers
The derivative of the function f is f'(x) = x^3 - 8x^2, and the original function f can be obtained by integrating the derivative.
The given derivative, f'(x) = x^3 - 8x^2, represents the rate of change of the function f with respect to x. To find the original function f, we need to integrate the derivative.
Integrating the derivative f'(x), we obtain:
f(x) = ∫(x^3 - 8x^2) dx
To integrate x^3, we add 1 to the exponent and divide by the new exponent:
∫x^3 dx = (1/4)x^4 + C1, where C1 is the constant of integration.
To integrate -8x^2, we use the same process:
∫-8x^2 dx = (-8/3)x^3 + C2, where C2 is another constant of integration.
Combining the two results, we have:
f(x) = (1/4)x^4 - (8/3)x^3 + C, where C = C1 + C2 is the overall constant of integration.
Thus, the original function f, corresponding to the given derivative, is f(x) = (1/4)x^4 - (8/3)x^3 + C.
Learn more about Derivative click here :brainly.com/question/18722002
#SPJ11
Augment is 5 1/3 feet tall how many inches tall is she
Answers
Answer:
64 inches tall
Step-by-step explanation:
We know in 1 foot, there are 12 inches.
We can convert 5 1/3 feet to 16/3 feet.
To do this you convert 5 feet to 15/3 feet and add it to 1/3 feet.
So we now have 16/3 feet and we will multiply by 12 to find the number of inches she is.
16/3 * 12 = 64 inches tall
Which expression is equivalent to X4 - 18X2 +81?
(x-g)(x² +9)
2.
of +9)(x2 +9)
3.
(9-x)(9+x2)
(x² - 9)(x² – 9)
4
Math
Answers
Let y=x^2
Then the equation becomes:
y^2 - 18y + 81
Factorise that to give you:
(y-9)(y-9) Or (y-9)^2
But remember, y=x^2. So the equation becomes:
(X^2-9)(X^2-9)
Hope this helped :)
Please help me ASAP!!! Answer both questions for example: 1= C and 2= A
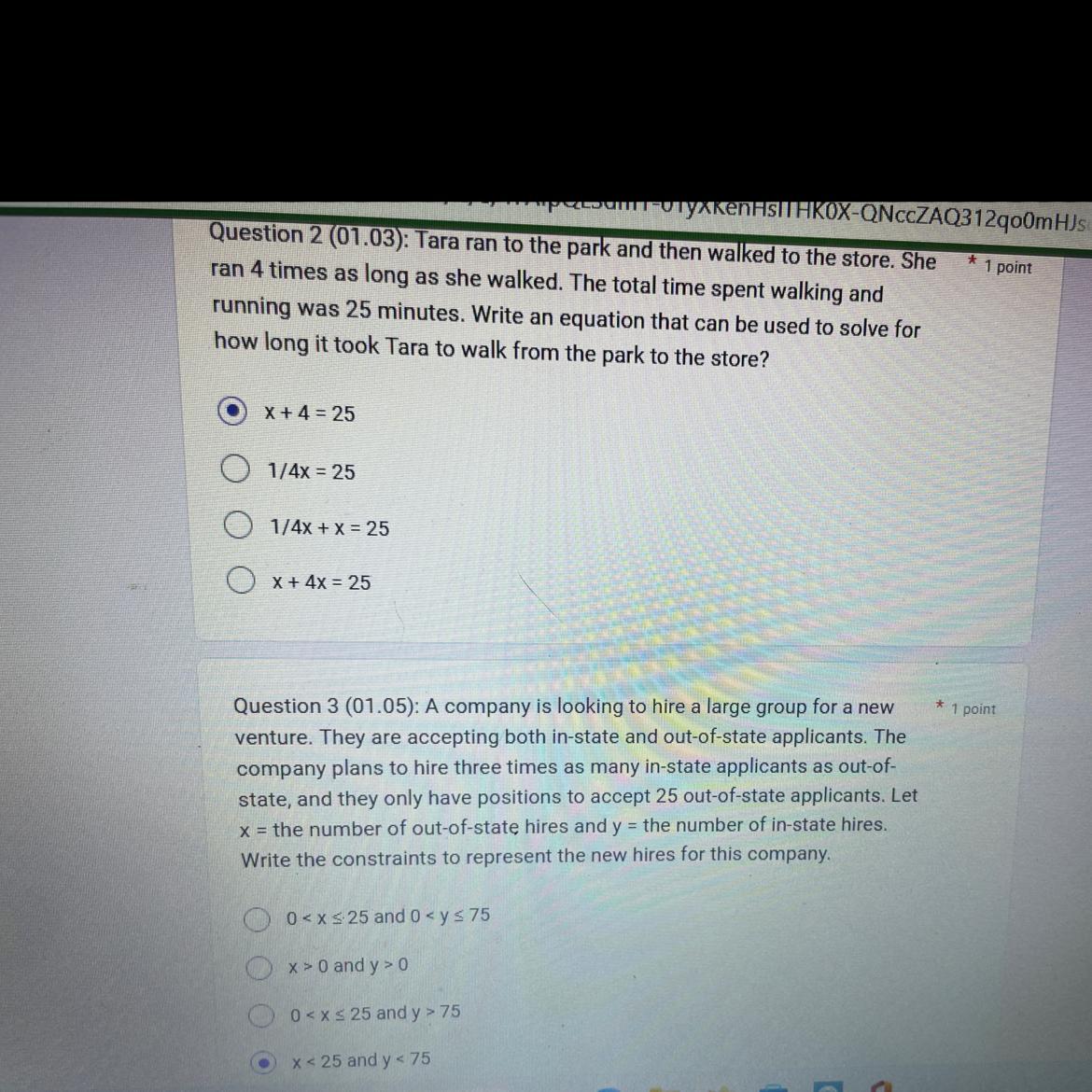
Answers
2. The equation is given as follows: x + 4x = 25.
3. The constrains are given as follows: 0 ≤ x ≤ 25, 0 ≤ y ≤ 75.
What is the equation in item 2?The time spent running is given by:
Running = 4x.
The time spent walking is one-fourth of the time spent walking, hence it is given by:
Walking = 4x/4 = x.
The total time is the sum of the times spent running and walking, hence the expression is presented as follows:
x + 4x = 25.
What are the constraints in item 3?The variables are given as follows:
x: number of out-of-state hires.y: number of in-state hires.You can accept at most 25 out-of-state hires, hence:
0 ≤ x ≤ 25
(as the number cannot be negative).
The company plans to have three times as many in-state hires, hence:
0 ≤ y ≤ 75.
As:
3 x 0 = 0.3 x 25 = 75.More can be learned about equations and constraints at https://brainly.com/question/18435162
#SPJ1
This class uses weighting, which you will need to account for in the calculation. test are worth 80% of the grade, and the class project is worth 20% of the grade. To calculate the final grade percentage you will need to add up the test scores; then divide by the total number of test points and then multiply by the weighted percentage. In a similar manner, calculate the percentage for the project. Then add the two totals together to get the final grade. Remember, students cannot earn more than 100%!
What is Student 3's numeric grade percentage? Use one decimal place and include the percent sign in your answer.
Answers
The student 3's numeric grade percentage is 95.6%.
The final grade for the students is calculated based on the test scores and the class project score.
The test is worth 80% and the project is worth 20% of the grade. To calculate the final grade percentage, the individual percentages of test and project are computed, then added together.
The result cannot exceed 100%.Let us calculate the weighted test score for student 3.
There were three tests each worth 100 points. The scores of student 3 are 91, 78, and 83.
We have to add up the test scores; then divide by the total number of test points and then multiply by the weighted percentage.
The weighted test score is:(91+78+83)/300 * 80% = 76.6%
We can now calculate the percentage for the project. Student 3 received a grade of 95%.
Therefore, the percentage for the project is: 95% * 20% = 19%.
Now, we add the weighted test score to the weighted project score to find the final grade for student 3. 76.6% + 19% = 95.6%.
Therefore, The final grade of student 3 is 95.6%
learn more about percentage from given link
https://brainly.com/question/24877689
#SPJ11
PLSSS HELP ME WILL MARK YOU BRAINLIEST

Answers
36+2L=60
2L= 60-36
2L= 24
L= 24/2
L= 12
12x18= 216
So the answer is A
If f(x) = the integral from 0 to x of dt/((t3+2)^1/2), which of the following is FALSE?
A) f(0) = 0 B) f is continuous at x for all x isgreater than or equal to 0 C) f(1) is greater than 0 D)f '(1) = 1/ (sqrt3) E) f(-1) is greater than or equalto 0
Answers
If f(x) is integral from 0 to x of (1/√(t³+2))dt, then the FALSE, statement is (e) f(-1) is greater than or equal to 0.
Option (a) is True, because the integral from 0 to 0 is zero, So, f(0) = 0.
Option (b) is True. The integrand is continuous for all x greater than or equal to 0, So, f(x) is differentiable and continuous for all x greater than or equal to 0.
Option (c) is True. The integrand is positive for all x, so the integral is positive for all x, including x = 1.
Option (d) is True. By using the Fundamental Theorem of Calculus and the Chain-Rule,
We have f'(x) = 1/√(x³+2).
So, f'(1) = 1/√3.
Option (e) is False, We see that integrand is undefined for negative values of t,
So, the integral from 0 to "x" is possible for non-negative values of x.
Therefore, f(x) is defined only for x greater than or equal to 0. In particular, f(-1) is undefined,
Therefore, option (e) is false.
Learn more about Integral here
https://brainly.com/question/32151209
#SPJ4
The given question is incomplete, the complete question is
If f(x) = the integral from 0 to x of (1/√(t³+2))dt, which of the following is FALSE?
(a) f(0) = 0,
(b) f is continuous at x for all x greater than or equal to 0,
(c) f(1) is greater than 0,
(d) f '(1) = 1/√3,
(e) f(-1) is greater than or equal to 0.
of the 60 questions, I got 80% right...How many questions did I get right?
Answers
Therefore you got 48 questions right.
pls answer i need help

Answers
Answer:
Step-by-step explanation:
its c
YALLL HELPP ME PLEASEE!!!!!!!!



Answers
Step-by-step explanation:
1. -5 not suree
2.50
my anwser could be wrong sooo...
How many factors of 2020 have more than 3 factors?
Answers
Answer:
Factors of 2020 are 1, 2, 4, 5, 10, 20, 101, 202, 404, 505, 1010. There are 11 integers that are factors of 2020. The biggest factor of 2020 is 1010.
There are 10, 20, 202, 404, 505, and 1010 factors of 2020 have more than 3 factors.
What is factorization?Factorization is expressing a mathematical quantity in terms of multiples of smaller units of similar quantities.
For an integer, factorization is decomposition of that integer in terms of smaller integers which when multiplied with each other give back that considered number. Those composing integers are called factors of that considered integers.
Also Prime factorization is when all those factors are prime numbers.
Thus, this factorization expresses an integer in terms of multiples of prime numbers.
Factors of 2020 are;
1, 2, 4, 5, 10, 20, 101, 202, 404, 505, 1010.
There are 11 integers that are factors of 2020.
We can see that the biggest factor of 2020 is 1010.
Learn more about factorization here:
https://brainly.com/question/10454590
#SPJ2