Answers
Answer:
H) 320 square units for the surface area
Step-by-step explanation:
20(5.2+5.25+4.5) + 2(1/2(4*5.25)) = 320
Related Questions
what percent is 272 out of 355?
Answers
Answer:
76.62 you might need to round though
Step-by-step explanation:
Assume that police estimate that 23% of drivers do not wear their seatbelts. They set up a safety roadblock, stopping cars to check for seatbelt use. They stop 20 cars during the first hour a. Find the mean, variance, and standard deviation of the number of drivers expected not to be wearing seatbelts. Use the fact that the mean of a geometric distribution is pi = 1/p and the variance is ohm^2 = p/q^2? b. How many cars do they expect to stop before finding a driver whose seatbelt is not buckled?
Answers
The mean of the number of drivers expected not to be wearing seatbelts is approximately 4.35, the variance is approximately 15.62, and the standard deviation is approximately 3.95 and they expect to stop approximately 4.35 cars before finding a driver whose seatbelt is not buckled.
a. To find the mean, variance, and standard deviation of the number of drivers expected not to be wearing seatbelts, we can model the situation using a geometric distribution.
Let's define a random variable X that represents the number of cars stopped until the first driver without a seatbelt is found. The probability of a driver not wearing a seatbelt is given as p = 0.23.
The mean (μ) of a geometric distribution is given by μ = 1/p.
μ = 1/0.23 ≈ 4.35
The variance (σ^2) of a geometric distribution is given by σ^2 = q/p^2, where q = 1 - p.
σ^2 = (0.77)/(0.23^2) ≈ 15.62
The standard deviation (σ) is the square root of the variance.
σ = √(15.62) ≈ 3.95
b. The expected number of cars they expect to stop before finding a driver whose seatbelt is not buckled is equal to the reciprocal of the probability of success (finding a driver without a seatbelt) in one trial. In this case, the probability of success is p = 0.23.
Expected number of cars = 1/p = 1/0.23 ≈ 4.35
To learn more about mean, variance and standard deviation go to:
https://brainly.com/question/30558769
#SPJ11
Please helppp. What’s the area and circumference??!

Answers
The value of EF is 26
What is segment of a circle?A segment of a circle can be defined as a region bounded by a chord and a corresponding arc lying between the chord's endpoints.There is minor segment and major segment.
Since the two arcs are equal, i.e arc EF = arc CD, therefore,
chord EF = chord CD
9x-1 = 41 - 5x
collecting like terms
9x +5x = 41+1
14x = 42
divide both sides by 14
x = 42/14
x = 3
Therefore EF = 41-5x
= 41-5×3
= 41-15
= 26
therefore the value of EF is 26
learn more about segment of circle from
https://brainly.com/question/30959436
#SPJ1
Please help solve the The answer to the question selected above is square centimeters. The answer to the other three questions is cubic centimeters part. Thanks!

Answers
a) It takes 350 cubic centimetres to fill the rectangular prism.
b) The capacity of the rectangular prism is 350 cm³.
c) It takes 340 square centimetres to cover the rectangular prism.
d) The rectangular prism contains 350 cm³.
a) We need to find the volume of the rectangular prism to determine how much it takes to fill it. The following formula provides the volume:
V = l × w × h
where the prism's length, breadth, and height are indicated by l, w, and h, respectively.
Substituting the given values, we get:
V = 5 cm × 7 cm × 10 cm
V = 350 cm³
Therefore, it takes 350 cubic centimetres to fill the rectangular prism.
b) The capacity of the rectangular prism is the same as its volume, which we calculated in part (a) to be 350 cm³.
c) To cover the rectangular prism, we need to find its surface area. The following formula determines a rectangular prism's surface area:
SA = 2lw + 2lh + 2wh
where the prism's length, breadth, and height are indicated by l, w, and h, respectively.
Substituting the given values, we get:
SA = 2(5 cm × 7 cm) + 2(5 cm × 10 cm) + 2(7 cm × 10 cm)
SA = 340 cm²
Therefore, it takes 340 square centimetres to cover the rectangular prism.
d) The rectangular prism contains the same amount of volume as its capacity, which we calculated in part (b) to be 350 cm³.
To learn more about rectangular prism, refer:-
https://brainly.com/question/21308574
#SPJ1
Which expression is equivalent to 4(x+2)?
6x
4(x)+4(2)
4(x)+4
8x
Answers
Answer:
B
Step-by-step explanation:
4(x+2)
4(x)+4(2)
4x+8
-hope it helps
(3) How many license plates can be made using either two uppercase English letters followed by four digits or two digits followed by four uppercase English letters? (4) How many strings of eight Engli
Answers
(3) To find the total number of license plates that can be made, we need to consider the two given cases separately:
Case 1: Two uppercase English letters followed by four digits In this case, we have 26 choices for each of the two letters (A-Z), and 10 choices for each of the four digits (0-9). Therefore, the total number of license plates that can be made in this case is: 26 * 26 * 10 * 10 * 10 * 10 = 6,760,000
Case 2: Two digits followed by four uppercase English letters In this case, we have 10 choices for each of the two digits (0-9), and 26 choices for each of the four letters (A-Z). Therefore, the total number of license plates that can be made in this case is: 10 * 10 * 26 * 26 * 26 * 26 = 45,697,600 To find the overall number of license plates, we add the results from both cases together: 6,760,000 + 45,697,600 = 52,457,600 Therefore, the total number of license plates that can be made using either two uppercase English letters followed by four digits or two digits followed by four uppercase English letters is 52,457,600.
Learn more about the License plates:
https://brainly.com/question/30809443
#SPJ11
help me with this ques. (need solution and answer both) thanks so much <3

Answers
Answer:
1.) 27a^11 + 18a^9 -72a^7
2.) 6p^4q^3 - 10p^3q + 4p^2q3
Step-by-step explanation:
1.) Distribute and do the math
-9a^5 x (-3a^6) - 9a^5 X (-2a^4) - 9a^5 x 8a^2
27a^11 + 18a^9 -72a^7
2.) Distribute and do the math
2pq^2q x 3p^2q^2 - sp^2q x 5p + 2p^2q x 2q^2
6p^4q^3 - 10p^3q + 4p^2q3
a Find a, and r for a geometric sequence {an} from the given information. az = 10 and ag = 80 Part 1 of 2 a = Part 2 of 2
Answers
The values for 'a' and 'r' in the geometric sequence {an} can be determined based on the given information. The first term 'a' is found to be 2, while the common ratio 'r' is calculated as 2.5.
In a geometric sequence, each term is obtained by multiplying the previous term by a constant value called the common ratio 'r'. Here, the given information states that az = 10 and ag = 80. Let's denote the subscript 'z' as the term number corresponding to the value 10, and the subscript 'g' as the term number corresponding to the value 80.
To find the first term 'a', we can use the fact that az = 10. Since a is the first term, it corresponds to the term with subscript 'z'. Therefore, we have a * r^(z-1) = az = 10.
Similarly, we can use the information ag = 80 to determine the value of 'r'. Since a is the first term, it corresponds to the term with subscript 'g'. Therefore, we have a * r^(g-1) = ag = 80.
By substituting the known values, we get two equations: a * r^(z-1) = 10 and a * r^(g-1) = 80.
Dividing these two equations, we can eliminate 'a' and solve for 'r'. (a * r^(g-1))/(a * r^(z-1)) = 80/10. Simplifying, we get r^(g-z) = 8.
Now, we can write the value 8 as a power of 'r'. Since 2^3 = 8, we have r^(g-z) = (2^3).
Comparing the exponents, we get g - z = 3.
Given that z and g are the subscripts for az and ag respectively, we can conclude that g - z = 3.
Now, we can solve the system of equations: a * r^(z-1) = 10 and g - z = 3.
From the second equation, we have g = z + 3. Substituting this into the first equation, we get a * r^(z-1) = 10.
Since we have g = z + 3, we can substitute this into the second equation again: a * r^(g-1) = 80.
From the first equation, we can express 'a' in terms of 'z': a = 10/r^(z-1).
Substituting this into the second equation, we get (10/r^(z-1)) * r^(g-1) = 80.
Simplifying, we have 10 * r^(g-z) = 80.
Using the value of g - z = 3, we get 10 * r^3 = 80.
Dividing both sides by 10, we obtain r^3 = 8.
Taking the cube root of both sides, we get r = 2.
Now that we have the value of 'r', we can substitute it back into the first equation: a * r^(z-1) = 10.
Substituting r = 2, we have a * 2^(z-1) = 10.
Since 2^(z-1) = 2^1 = 2, we can solve for 'a' by dividing both sides by 2: a = 10/2 = 5.
Therefore, the first term 'a' is 5 and the common ratio 'r' is 2.
Learn more about geometric sequence here : brainly.com/question/27852674
#SPJ11
14. (10.0 points) Given f(x)=sin(2πx), when x = 0.3, f(x) = 0.951057. Approximate the value of f(0.2) using the first two terms in the Taylor series and Vx=0.1. (Write your answer to 6 decimal points).
Answers
Given the function f(x)=sin(2πx), with x = 0.3, f(x) = 0.951057. The objective is to approximate the value of f(0.2) using the first two terms in the Taylor series and Vx=0.1.
We know that the Taylor series for a function f(x) can be written as:f(x)=f(a)+f′(a)(x−a)+f′′(a)2(x−a)2+…+f(n)(a)n!(x−a)n+…The first two terms of the Taylor series are given by:f(x)=f(a)+f′(a)(x−a)The first derivative of f(x) is given by:f′(x)=2πcos(2πx)On substituting x = a = 0.1, we get:f′(0.1) = 2πcos(2π * 0.1) = 5.03118603447The value of f(x) at a=0.1 is given by:f(0.1) = sin(2π * 0.1) = 0.587785252292With a=0.1, the first two terms of the Taylor series become:f(x)=0.587785252292+5.03118603447(x−0.1) = 0.587785252292+0.503118603447x−0.503118603447×0.1Using x=0.2 and substituting the values of a and f(a) in the equation above, we get:f(0.2)=0.587785252292+0.503118603447*0.2−0.503118603447×0.1=0.712261After approximating the value of f(0.2) using the first two terms in the Taylor series,
we can conclude that the value of f(0.2) = 0.712261 with a = 0.1, with an error of approximately 0.012796.
To know more about Taylor series visit
https://brainly.com/question/32235538
#SPJ11
pls help!!! i will give brainliest!!

Answers
Answer:
About 84 liters
Step-by-step explanation:
Length*width*fill
24*19*0.75
111.51 liters*0.7=83.62=83.6 or 84 (estimated)
All in liters
Hope this helped :)
Answer:
It is about 84 litres to be exact 83.62
Step-by-step explanation:
Hope this helped have an amazing day!
NEED HELP! Find the area of the quadrilateral. (Geometry)
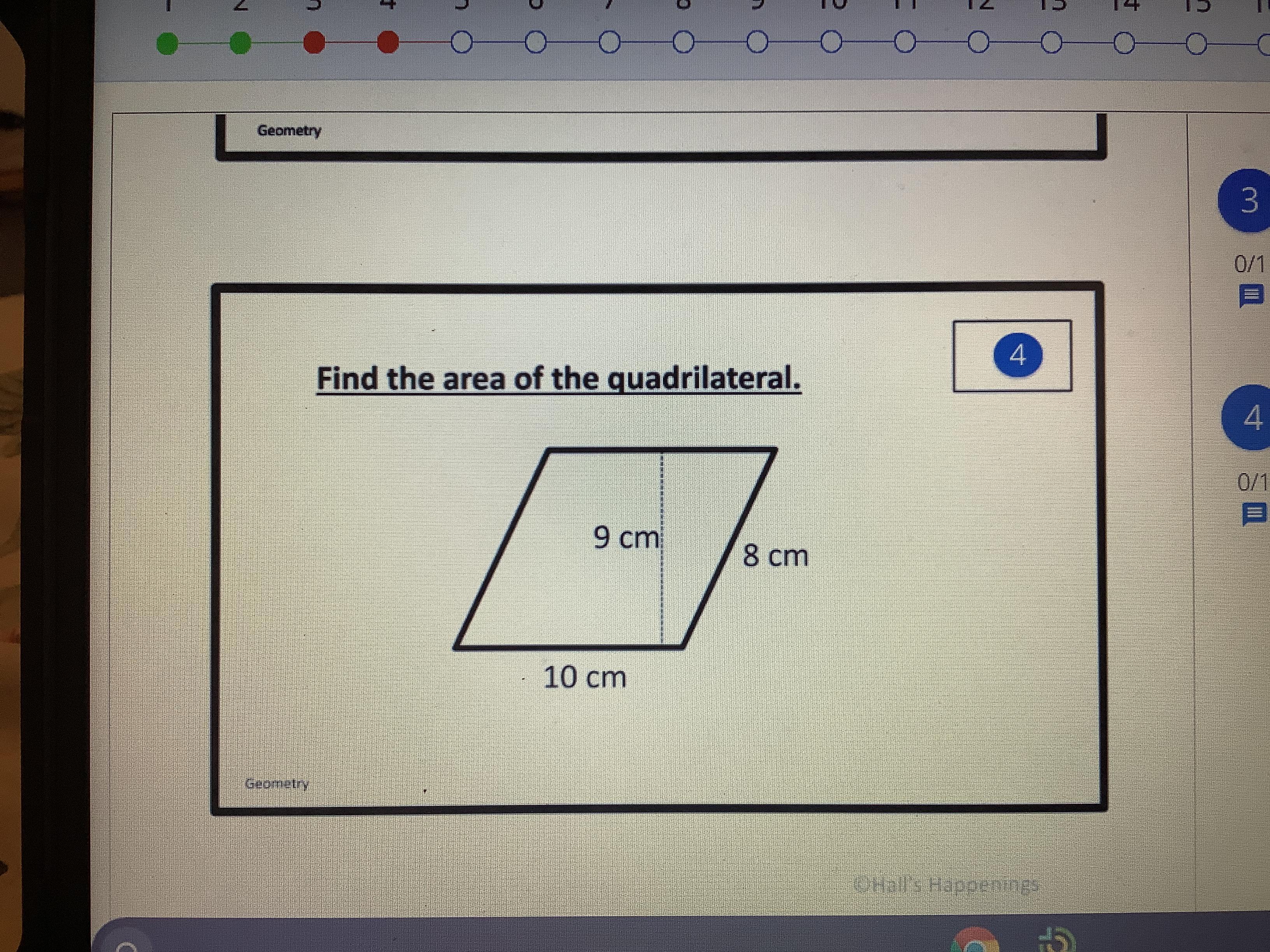
Answers
Answer:
90 \(cm^{2}\)
Step-by-step explanation:
It's a parallelogram
So area of a parallelogram = base x height
A = 9 x 10
A = 90
Hope that helps!
Answer:
90
Step-by-step explanation:
Since this is a parallelogram, it's just A = BH, which they already give you both, the base and the height.
Base : 10
Height : 9
10x9=90
compute the derivative of your cost function in problem 9. the derivative function will contain one or more of the letters x, n, p, b, c
Answers
The derivative of the cost function with respect to the production quantity is given by the expression dC/dx = np + c/x^2, where x, n, p, b, and c are constants is the answer.
The derivative of the cost function in problem 9 is a function that expresses the rate of change of the cost function with respect to a unit change in the production quantity.
Suppose that the cost function for producing x units of a product is given by the formula: C(x) = npx + b + c/x
Where n is the number of items produced in a batch, p is the cost per item, b is the fixed cost, and c is the variable cost.
Using the power rule of differentiation, we can differentiate the cost function term by term as follows: dC/dx = d/dx(npx) + d/dx(b) + d/dx(c/x)= np(d/dx(x)) + 0 - c(d/dx(1/x^1))= np + c/x^2
Therefore, the derivative of the cost function with respect to the production quantity is given by the expression dC/dx = np + c/x^2, where x, n, p, b, and c are constants.
The derivative function contains the letters x, n, p, b, and c.
know more about derivative
https://brainly.com/question/29144258
#SPJ11
Sarah invests $2,050 paying 6.75% compunded
continuously. How long will it taks Sarah's
investment to double?
Answers
Answer:
If the interest per quarter is 4% (but interest is only compounded annually), then it will take (72 / 4) = 18 quarters or 4.5 years to double the principal.
Step-by-step explanation:
7 times what equals 12
Answers
Answer:
12/7Step-by-step explanation:
Let the required number be 'n'.
Then, we need to find what the value of n is.
According to the question,
7 x n = 12Multiply both sides by 1/7.
7 x n x 1/7 = 12 x 1/77/7 x n = 12/7n = 12/7How do you find eigenvalues and eigenvectors of a matrix?
Answers
Identifying Eigenvalues and Eigenvectors, A should be a n x n matrix. By resolving the det(λI−A)=0 problem, first determine the eigenvalues of A. Find the fundamental solutions to (λI−A)X=0 to determine the fundamental eigenvectors X≠0 for each.
In linear algebra, a nonzero vector is said to have an eigenvector, or characteristic vector, when a linear transformation is applied to it; this characteristic vector only changes by a scalar amount. The scaling factor for the eigenvector is known as the associated eigenvalue, frequently represented by the symbol. Linear transformations are made intelligible by the usage of eigenvectors. Eigenvectors can be thought of as a non-directional stretching or compressing of an X-Y line chart. In mathematics, eigenvalues are regarded as the factor by which a transformation is stretched, whereas eigenvectors are the real non-zero eigenvalues that point in the direction stretched by the transformation. The direction of the transformation is negative if the eigenvalue is negative.
To know more about Eigenvectors here
https://brainly.com/question/15423383
#SPJ4
Please help, I just started trig. Thanks!

Answers
Answer:
About 3.052 units
Step-by-step explanation:
I presume you won't need this explanation now, but just in case;
If we draw triangle MNK, as MN = NK we know is isosceles. Now let's draw an altitude to MK so that it splits MK into two congruent parts (5/2 = 2.5). Given M<N = 110 degrees the altitude would split the angle into two congruent angles as well (Coincidence Theorem)---- 110/2 = 55 degrees.
Now let's study the smaller triangles, and take one as an example. Remember sin(theta) = opp/hyp. Applying this we have theta as 55 degrees, the opposite side as 2.5, and the hypotenuse is yet to be found (MN);
sin(55°)= 2.5/MN,
x = 2.5/sin(55°) ≈3.052
Pls help. Will mark brainliest

Answers
Answer:
see below (I hope this helps!)
Step-by-step explanation:
p² = 4x² * (q(1 + r² / y²) / S)
p²S = 4x² * q(1 + r² / y²)
p²S / 4x²q = 1 + (r² / y²)
p²S / 4x²q - 1 = r² / y²
y² = r² / (p²S / 4x²q - 1)
y = √( r² / (p²S / 4x²q - 1) = √(r²4x²q / (p²S - 4x²q))
which classification describes the following system of equations x=5 y=6 -x-y+z=0
?
A. inconsistent and dependent
B. consistent and dependent
C. consistent and independent
D. inconsistent and independent
Answers
The system of equations has one solution, so it is consistent and independent, the correct option is C.
What is the classification of the system of equations?
Here we have the system of equations:
x = 5
y = 6
-x - y + z = 0
By replacing the first and second equations into the third one, we get:
-5 - 6 + z = 0
-11 + z = 0
z = 11
So the solution is (5, 6, 11)
So it is consistent, and it is independent as clearly, the equations are linearly independent (system of 3 equations with 3 variables having only one solution).
Then the correct option is C.
Learn more about systems of equations:
https://brainly.com/question/13729904
#SPJ1
\(\bold{Heya~!}\)
\(\sf{What~is~9x~12~x~7~+~2x~?\)
✏ \(\underline{\large \huge{\mathfrak{Note:~Explanation~your~answers,~With~your~own~words.}}}\)
Thanks~
Answers
The tree diagram represents an
experiment consisting of two trials.
Enter the probability to the hundredths place.
Do not round.
P(D) = [?]
PLEASE HELP FAST!!

Answers
The value of the probability {(D) is 0.74
How to determine the values of the probabilitiesFrom the question, we have the following parameters that can be used in our computation:
The tree diagram
Using the above as a guide, we have the following:
P(D and A) = 0.6 * 0.7 = 0.42
P(D and B) = 0.4 * 0.8 = 0.32
Add the probability values
so, we have the following representation
P(D) = 0.42 + 0.32
Evaluate
P(D) = 0.74
Hence, the probability is 0.74
Read more about probability
https://brainly.com/question/251701
#SPJ1
a researcher recorded reaction time to respond to a sound. if the data of the research subjects are presented in a frequency distribution graph, what type of graph should be used?
Answers
If the data of the research subjects are presented in a frequency distribution graph, a histogram-type graph should be used.
If the data are presented in a frequency distribution graph, then the type of graph that should be used is a histogram. A histogram is a type of bar graph that displays the distribution of a continuous variable by dividing the range of values into intervals, and bins, and counting the number of observations that fall within each bin.
If the academic majors were nominal a bar graph could also be used to display the frequency of each major. In a bar graph, each category would be plotted on the horizontal axis, and the frequency of students in each category would be plotted on the vertical axis.
To learn more about the histogram
https://brainly.com/question/30701461
#SPJ4
Use the proportion d/180° = r radians /πradians * . Find the equivalent degree measure or radian measure. 10°
Answers
The equivalent radian measure for 10 degrees is approximately 0.1745 radians.
To find the equivalent radian measure for 10 degrees using the given proportion, we can set up the equation:
d/180° = r/π radians
Plugging in 10 degrees for d, the equation becomes:
10°/180° = r/π radians
Simplifying the left side of the equation:
1/18 = r/π radians
To find the value of r, we can cross-multiply:
r = (1/18) π radians
Calculating the right side of the equation:
r ≈ 0.1745 radians (rounded to four decimal places)
Therefore, the equivalent radian measure for 10 degrees is approximately 0.1745 radians.
Learn more about Radian here:
https://brainly.com/question/28990400
#SPJ11
Which is the approximate measure of angle ACB?
31.0°
36.9°
53.1°
59.0°

Answers
Answer:
53.1
Step-by-step explanation:
i just took the test
Answer:
53.10
Step-by-step explanation:
What will be the coordinates of N after a 90° counterclockwise rotation around the origin?
A. (-7,-3)
B. (-7,0)
C. (3,7)
D. (-3,-7)

Answers
Answer:
A. (-7,-3)
D.(-3,-7) If clockwise
which eq has no real solutions? \(2 = \sqrt{x + 3 + 5} \)\(4 = \sqrt{x - 1 - 2} \)\(1 = \sqrt[3]{x + 1 + 2} \)\(6 = \sqrt[3]{x - 2 - 1} \)
![which eq has no real solutions? [tex]2 = \sqrt{x + 3 + 5} [/tex][tex]4 = \sqrt{x - 1 - 2} [/tex][tex]1](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/SOoE16U6u2bKLAg6znd71q7xGvHC48Cr.png)
Answers
Let's solve each equation.
\(2=\sqrt[]{x+3}+5\)First, we subtract 5 on each side.
\(\begin{gathered} 2-5=\sqrt[]{x+3}+5-5 \\ -3=\sqrt[]{x+3} \end{gathered}\)You can observe that we've got x = 6 as a solution, however, this is not completely true because at the beginning we got a square root equal to a negative number and that doesn't have a solution in the real numbers. Square roots can't give a negative result, that's why.
The second equation is
\(4=\sqrt[]{x-1}-2\)First, we add 2 on each side.
\(\begin{gathered} 4+2=\sqrt[]{x-1}-2+2 \\ 6=\sqrt[]{x-1} \end{gathered}\)Then, we elevate the equation to the square power.
\(\begin{gathered} 6^2=(\sqrt[]{x-1})^2 \\ 36=x-1 \\ x=36+1=37 \end{gathered}\)The second equation has a real solution.
The third equation is
\(\begin{gathered} 1=\sqrt[3]{x+1}+2 \\ 1-2=\sqrt[3]{x+1} \\ -1=\sqrt[3]{x+1} \\ (-1)^3=(\sqrt[3]{x+1})^3 \\ -1=x+1 \\ x=-1-1=-2 \end{gathered}\)The third equation has a real solution.
The fourth equation is
\(\begin{gathered} 6=\sqrt[3]{x-2}-1 \\ 6+1=\sqrt[3]{x-2} \\ 7=\sqrt[3]{x-2} \\ 7^3=(\sqrt[3]{x-2})^3 \\ 343=x-2 \\ x=343+2=345 \end{gathered}\)The fourth equation has a real solution.
Why do we need to construct table in getting POPULATION VARIANCE?
Answers
Answer:
it's helps it by standing
-0.5f - 4.52 = -25.52 + f HELP PLEASE
Answers
Answer:
-0.5f - 4.52 = -25.52 + 1f
-1.5f = 21
f = 14
Answer:
14
Step-by-step explanation:
-4.52 + 25.52 = f + 0.5f
21 = 1.5f
f = 14
How do you write 400 in scientific notation?
Answers
Answer: 4x10^2
Step-by-step explanation:
Instructions: Using the image, find the slope of the line. Reduce all fractions and enter using a forward slash (i.e."/"). If the slope is undefined, enter "undefined."

Answers
Answer:
Step-by-step explanation:
(-5, 4) (4, -5)
(-5 - 4)/(4 + 5)= -9/9= -1
Answer:
(-5, 4) (4, -5)
(-5 - 4)/(4 + 5)= -9/9= -1
find the cube root
\(3 \sqrt{729} \)
Answers
Answer:
The cube root would be 9. Cubed is just like squared, but a number multiplied 3 times to get the number 729.
Step-by-step explanation:
A way to solve it is:
729 / 3 = 243
243 / 3 = 81
81 / 3 = 27
27 / 3 = 9
9^3 = 729
9 • 9 = 81
81 • 9 = 729
Answer:
9
Step-by-step explanation:
