73 is what percent of 800
Answers
Answer:
0.09125%
Step-by-step explanation:
Divide 73 by 800 and you will get 0.09125
Answer:
It should be %9.75
Related Questions
A truck can be rented from company a for $110 a day plus $0.70 per mile, company b charges $80 a day plus $0.80 per mile to rent the same truck. find the number of miles in a day at which the rental costs for company a and company b are the same.
Answers
The number of miles for same rental costs are 300 miles.
Let the number of miles be x.
Firstly calculating the cost of Company a -
Total cost = One day cost + Number of miles × Cost per mile
Total cost = 110 + 0.70x
Calculating the cost of Company b -
Total cost = One day cost + Number of miles × Cost per mile
Total cost = 80 + 0.80x
Now, for the same rental cost, we will equate the two expressions. This will calculate the value of x.
110 + 0.70x = 80 + 0.80x
Rearranging the expression -
110 - 80 = 0.80x - 0.70x
Performing subtraction
30 = 0.10x
Shifting the values on other side of equation
x = 30/0.10
Performing division
x = 300
Hence, the rental cost for both companies will be same for 300 miles.
Learn more about relating the equation -
https://brainly.com/question/27893282
#SPJ4
Can someone help on this? Thank youu;)

Answers
Answer:
2^(3/7)
Step-by-step explanation:
For these types of questions, what is inside the root is the numerator, and what is on top is the denominator.
3 is in the root, so it is the numerator
7 is outside the root, so it is the denominator
Therefore, The answer is 2^(3/7)
I need help! 50 points!

Answers
The equation of this sinusoidal function is either
f(x) = a sin(bx) + c
or
f(x) = a cos(bx) + c
Either way, the plot of f9x) has amplitude a, period 2π/b, and midline y = c.
If the period is π/2, then
2π/b = π/2 ⇒ b = 4
If the maximum value is 10 and the minimum value is -4, then
-4 ≤ a sin(4x) + c ≤ 10
-4 - c ≤ a sin(4x) ≤ 10 - c
-(4 + c)/a ≤ sin(4x) ≤ (10 - c)/a
Recall that sin(x) is bounded between -1 and 1. So we must have
-(4 + c)/a = -1 ⇒ a = c + 4
(10 - c)/a = 1 ⇒ a = -c + 10
Combining these equations and eliminating either variable gives
a + a = (c + 4) + (-c + 10) ⇒ 2a = 14 ⇒ a = 7
a - a = (c + 4) - (-c + 10) ⇒ 0 = 2c - 6 ⇒ c = 3
Finally, we have either
f(x) = a sin(bx) + c ⇒ f(0) = c = 3
or
f(x) = a cos(bx) + c ⇒ f(0) = a + c = 3
but the cosine case is impossible since a = 7.
So, the given function has equation
f(x) = 7 sin(4x) + 3
Tina´s family is taking a road trip. If they travel for 3.5 hours on the first day, 2 hours on the second day 4.5 hours on the third day, and 4 hours on the fourth day, how long did they drive overall
Answers
Answer:
14.
Step-by-step explanation:
this a addition problem since it says "overall".
you simply add them.
Half of the smaller of two consecutive even integers is equal to two more than the larger integer
Answers
By solving a linear equation we can see that:
The smaller number is -8The larger number is -6How to find the two numbers?
Here we have two consecutive even integers, we can write these as x and x + 2
We know that half of the smaller of the two is equal to 2 more than the larger one, this can be writen as:
x/2 = (x + 2) + 2
Now we can solve that linear equation for x:
x/2 = x + 2 + 2
x/2 = x + 4
-4 = x - x/2
-4 = x/2
-4*2 = x = -8
The smaller number is -8
The larger number is -8 + 2 = -6
If you want to learn more about linear equations:
https://brainly.com/question/1884491
#SPJ1
My son needs help on finding percents. example. what is 53% of 80?
Answers
According to the information given in the exercise, you know that the 100% is 80.
Let be "x" the number that is the 53% of 80.
By definition, you can write 53% as a Decimal number by dividing it by 100. Then, this is:
\(\frac{53}{100}=0.53\)You can write 100% as a Decimal number:
\(\frac{100}{100}=1\)Knowing the above, you can set up the following proportion:
\(\frac{80}{1}=\frac{x}{0.53}\)Now you must solve for "x":
\(\begin{gathered} (0.53)(80)=x \\ x=42.4 \end{gathered}\)The answer is:
\(42.4\)You and your friend both get a candy cane from scrooge enterprises, you may assume that they are independent of each other. assuming that the weights of all the candy canes are approximately normally distributed, what is the probability that one of the candy canes is more than 1 gram heavier than the other?
Answers
The total probability that one of the candy canes is more than 1 gram heavier than the other is:
P(Z > 1 or Z < -1) = P(Z > 1) + P(Z < -1) = 1 - Φ((1 - μ_Z)/σ_Z) + Φ((-1 - μ_Z)/σ_Z)
Let's assume the mean weight of a candy cane is μ and its standard deviation is σ. Then, the weights of both of your candy canes are approximately normally distributed with mean μ and standard deviation σ.
Let X and Y be the weights of your candy cane and your friend's candy cane, respectively. The difference between their weights, Z = X - Y, is also approximately normally distributed with mean μ_Z = μ_X - μ_Y = 0 and standard deviation σ_Z = √(σ_X^2 + σ_Y^2) = √(2)σ.
The probability that one of the candy canes is more than 1 gram heavier than the other is equal to the probability that Z > 1 or Z < -1. This can be calculated using the cumulative distribution function of the standard normal distribution:
P(Z > 1) = 1 - P(Z < 1) = 1 - Φ((1 - μ_Z)/σ_Z)
P(Z < -1) = Φ((-1 - μ_Z)/σ_Z)
Where Φ is the cumulative distribution function of the standard normal distribution.
So, the total probability that one of the candy canes is more than 1 gram heavier than the other is:
P(Z > 1 or Z < -1) = P(Z > 1) + P(Z < -1) = 1 - Φ((1 - μ_Z)/σ_Z) + Φ((-1 - μ_Z)/σ_Z)
Note that this assumes that the weights of all the candy canes are approximately normally distributed.
Learn more about probability here: brainly.com/question/30034780
#SPJ4
I need help please thanks

Answers
what do you need help on ?????......???????..............
A television station serves residents of three cities located at J(5,2), K(-7, 2),
and L(-5, -8). The station wants to build a new broadcast facility that is
equidistant from the three cities. What are the coordinates of the location
where the facility should be built?
Answers
The coordinates of the location where the facility should be built are (7, 0).
We are given the coordinates of three cities J(5, 2), K(-7, 2) and L(-5, -8).
A television station wants to build a new broadcast facility that is equidistant from the three cities.
We need to find out the coordinates of the location where the facility should be built.
We can use the distance formula to find the distance between two points (x1, y1) and (x2, y2):d
= √[(x₂ - x₁)² + (y₂ - y₁)²]
Let (x, y) be the coordinates of the broadcast facility.
We know that the distance from the facility to city J is equal to the distance from the facility to city K, and also equal to the distance from the facility to city L.
Using the distance formula, we can write these three equations:√[(x - 5)² + (y - 2)²]
= √[(x + 7)² + (y - 2)²] [Distance from facility to city J = distance from facility to city K]
√[(x - 5)² + (y - 2)²]
= √[(x + 5)² + (y + 8)²]
[Distance from facility to city J = distance from facility to city L]√[(x + 7)² + (y - 2)²]
= √[(x + 5)² + (y + 8)²]
[Distance from facility to city K = distance from facility to city L]
Squaring both sides of these equations, we get: (x - 5)² + (y - 2)² = (x + 7)² + (y - 2)² ...
(1)Simplifying this equation, we get: x = -1
Similarly, (x - 5)² + (y - 2)² = (x + 5)² + (y + 8)² ...
(2)Simplifying this equation, we get: x² + y² - 10x - 4y + 90 = 0
Similarly, (x + 7)² + (y - 2)² = (x + 5)² + (y + 8)² ..
.(3)Simplifying this equation, we get: x² + y² - 4x - 10y - 6 = 0
Now, we need to solve equations (2) and (3) for y and x respectively.x² + y² - 10x - 4y + 90 = 0
[Equation (2)]x² + y² - 4x - 10y - 6 = 0 [Equation (3)]
Multiplying equation (2) by 10, and equation (3) by 4,
we get:10x² + 10y² - 100x - 40y + 900 = 0 ...(4)
4x² + 4y² - 16x - 40y - 24 = 0 ...
(5)Subtracting equation (5) from equation (4),
we get:6x² + 6y² - 84x + 924 = 0
Simplifying this equation by dividing both sides by 6,
we get:x² + y² - 14x + 154 = 0
Completing the square, we get:(x - 7)² + y² = 95
This is the equation of a circle with center at (7, 0) and radius √95 units.
Therefore, the coordinates of the broadcast facility are (7, 0).
To know more about coordinates visit:
https://brainly.com/question/29204164
#SPJ11
Michael has a bag of marbles. The frequency of selecting each color is recorded in the table below.
Outcome Frequency
Green 4
Black 6
Orange 5
Based on the given frequency, determine the experimental probability of selecting an orange marble.
0.27
0.33
0.40
0.67
Answers
The probability of selecting an orange marble is 0.33.
Option B is the correct answer.
What is probability?It is the chance of an event to occur from a total number of outcomes.
The formula for probability is given as:
Probability = Number of required events / Total number of outcomes.
We have,
The number of times each marble is selected.
Green = 4
Black = 6
Orange = 5
Total number of times all marbles are selected.
= 4 + 6 + 5
= 15
Now,
The probability of selecting an orange marble.
= 5/15
= 1/3
= 0.33
Thus,
The probability of selecting an orange marble is 0.33.
Learn more about probability here:
https://brainly.com/question/14099682
#SPJ1
What is the probability of pulling jack, queen, or king from a deck of cards?
Answers
Answer:
Step-by-step explanation:I don't say u must have to mark my ans as brainliest but if it has really helped u plz don't forget to thnk me....

Someone please please help

Answers
Answer:
k=60
step-by step explanation:
a triangles angles should all add up to 180.
so:
78+42=120
180-120=60
this would be the angel k.
The angle h would be 42 and angle g would be 78
Please help.
Algebra.

Answers
A point i reflected in the x-axi followed by the y-axi. The reflected point i (-3, "-4). " What i the original point?
Answers
When the original point is mirrored in the x-axis, it becomes (-3,4).
What is coordinate?The horizontal and vertical distances from the two reference axes are used to define the location of a point on a coordinate plane. The x-value and y-value are often denoted as (x,y). To find the coordinates of a point in a coordinate system, do the inverse. Start at the point and trace a vertical line up or down to the x-axis. There you have your x-coordinate. Then repeat the process, but this time follow a horizontal line to determine the y-coordinate.
Here,
The reflected point= (-3,-4)
A point reflected in the x-axis followed by the y-axis,
=(-3,4)
The original point is (-3,4) when point reflected in the x-axis followed by the y-axis.
To know more about coordinates,
https://brainly.com/question/28806463
#SPJ4
Identify the simplest form of each ratio
24 : 32
56:49
9:12
36:48
18:27
16:14
20:30
48:42
24:36

Answers
Answer:
38:48=3:4
48:42= 8:7
20:30= 2:3
16:14=8:7
9:12=3:4
56:49=8:7
24:32=3:4
24:36=2:3
18:27=2:3
Step-by-step explanation:
The simplest form of ratio 18:27 , 20:30 , and 24:36 is 2;3.
The simplest form of ratio 24:32, 9;12, and 36:48. is 3;4.
The simplest form of ratio 56:49 , 16:14 , and 48;42 is 8;7.
We have to determine, the simplest form of each ratio.
The given ratios are; 24:32, 56:49 , 9:12 , 36:48 , 18:27 , 16:14 , 20:30 , 48:42 , 24:36.
The simplest form of the ratio 24;32 is,
\(\dfrac{24}{32} = \dfrac{12}{16} = \dfrac{6}{8} = \dfrac{3}{4}\)
The simplest form of the ratio 56;49 is,
\(\dfrac{56}{49} = \dfrac{8}{7}\)
The simplest form of the ratio 9;12 is,
\(\dfrac{9}{12} = \dfrac{3}{4}\)
The simplest form of the ratio 36;48 is,
\(\dfrac{36}{48} = \dfrac{18}{24} = \dfrac{9}{12} = \dfrac{3}{4}\)
The simplest form of the ratio 18;27 is,
\(\dfrac{18}{27} = \dfrac{6}{9} = \dfrac{2}{3}\)
The simplest form of the ratio 16;14 is,
\(\dfrac{16}{14} = \dfrac{8}{7}\)
The simplest form of the ratio 20;30 is,
\(\dfrac{20}{30} = \dfrac{2}{3}\)
The simplest form of the ratio 48;42 is,
\(\dfrac{48}{42} = \dfrac{24}{21} = \dfrac{8}{7}\)
The simplest form of the ratio 24;36 is,
\(\dfrac{24}{36} = \dfrac{12}{18} = \dfrac{6}{9} = \dfrac{2}{3}\)
To know more about Ratio and proportion click the link given below.
https://brainly.com/question/25561616
What is the value of x?
x + 5
X
X-2
x + 1

Answers
The most appropriate choice for Basic Proportionality Theorem will be given by -
x = 5 is the correct answer
What is Basic Proportionality Theorem?
If a line is drawn parallel to third side of a triangle, intersecting the other two sides of the triangle, the other two sides are divided in the same ratio.
Here,
In the figure, two parallel lines are given
By Basic Proportionality Theorem,
\(\frac{x}{x+5} = \frac{x-2}{x+1}\\\)
\(x(x +1) = (x - 2)(x + 5)\\x^2 +x = x^2 + 5x - 2x -10\\x = 3x -10\\3x - x = 10 \\ 2x = 10\\x = \frac{10}{2}\\x = 5\)
x = 5 is the correct answer
To learn more about Basic Proportionality Theorem, refer to the link-
https://brainly.com/question/14417137
#SPJ13
Alex can run 26 miles in 6 hours, Bethany can run 26 miles in 5 hours and Carol can run 26 miles in 4 hours. If they start together and each run at their constant speeds, how many hours does it take for them to finish a total of 26 miles among the three of them
Answers
It takes approximately 86.67 hours for Alex, Bethany, and Carol to collectively finish a total of 26 miles. This is determined by calculating the harmonic mean of their individual running speeds.
To determine how many hours it takes for Alex, Bethany, and Carol to collectively run a total of 26 miles, we need to consider their individual running speeds. Alex runs at a rate of 26 miles in 6 hours, Bethany runs at a rate of 26 miles in 5 hours, and Carol runs at a rate of 26 miles in 4 hours.
To find the total time it takes for them to finish 26 miles together, we can calculate the harmonic mean of their individual running speeds. The harmonic mean is used because it accounts for the different rates at which they run.
The formula for the harmonic mean is given by:
Harmonic Mean = Total Distance / (1 / Speed1 + 1 / Speed2 + 1 / Speed3)
Substituting the values, we have:
Harmonic Mean = 26 / (1 / 6 + 1 / 5 + 1 / 4)
To simplify the equation, we find the common denominator:
Harmonic Mean = 26 / ((5 + 6 + 7) / 60)
Harmonic Mean = 26 / (18 / 60)
Harmonic Mean = 26 / (3 / 10)
Harmonic Mean = 26 * (10 / 3)
Harmonic Mean ≈ 86.67
Therefore, it takes approximately 86.67 hours for Alex, Bethany, and Carol to collectively finish a total of 26 miles.
To know more about the harmonic mean, refer here:
https://brainly.com/question/26491057#
#SPJ11
At a town meeting, the ratio of dark-haired people to blond-haired people to red-haired people is 42 : 37 : 3. If there are 1,312 people at the meeting, how many have each color hair?
Answers
Answer:
672 had dark hair, 592 had blond hair, and 48 had red hair
Step-by-step explanation:
To solve this problem, we need to first find the total number of people for each hair color based on the given ratio.
Let's start by finding the common factor that we can use to scale the ratio up to the total number of people, which is 1,312:
42 + 37 + 3 = 82
We can then divide 1,312 by 82 to get the scaling factor:
1,312 ÷ 82 = 16
This means that for every 16 people, there are 42 with dark hair, 37 with blond hair, and 3 with red hair.
To find the actual number of people with each hair color in the town meeting, we can multiply the scaling factor by the number of people for each hair color in the ratio:
Dark-haired people: 42 × 16 = 672
Blond-haired people: 37 × 16 = 592
Red-haired people: 3 × 16 = 48
Therefore, there are 672 people with dark hair, 592 people with blond hair, and 48 people with red hair at the town meeting.
Given the following prices, explain why brand b is the better buy. (hint: 16 ounces = 1 pound and 1 pound = 453. 59 grams) brand a: 54 ounces for $4. 89 brand b: pounds for $3. 91 brand c: 910 grams for $3. 10.
Answers
Brand B is the better buy because it offers the most ounces for the lowest price.
To compare the prices of the three brands, we need to convert them to a common unit of measurement. Brand A is priced at $4.89 for 54 ounces, Brand B is priced at $3.91 for 16 ounces, and Brand C is priced at $3.10 for 910 grams. Since 16 ounces is equivalent to 1 pound and 1 pound is equivalent to 453.59 grams, we can convert the weight of Brand B and C to ounces. 910 grams is equivalent to 2.01 pounds, which is equivalent to 32.16 ounces.
A.
54oz, convert to lb
54/16=3.375lb
find per lb
4.89/3.375=$1.4488888 per lb
B.
2 and 3/4=2.75, 3.91/2.75=$1.42181 per lb
C. 910/453.59=2.00621lb
3.10/2.00621=$1.545 per lb
compare
A: $1.4488888 per lb
B: $1.42181 per lb
C: $1.545 per lb
It is observed from the above calculation that Brand B have lowest price per unit on ounce.
To learn more about the unit of measurement click below:
https://brainly.com/question/15402847#
#SPJ4
Show that if \( |z| \leq 1 \), then \[ |z-1|+|z+1| \leq 2 \sqrt{2} \]
Answers
To prove the inequality \(\(|z-1| + |z+1| \leq 2\sqrt{2}\)\) when \(\(|z| \leq 1\)\), we can use the triangle inequality. Let's consider the point\(\(|z| \leq 1\)\) in the complex plane. The inequality states that the sum of the distances from \(\(z\)\) to the points \(\(1\)\) and \(\(-1\)\) should be less than or equal to \(\(2\sqrt{2}\)\).
Let's consider two cases:
Case 1: \(\(|z| < 1\)\)
In this case, the point \(\(z\)\) lies strictly within the unit circle. We can consider the line segment connecting \(\(z\)\) and \(1\) as the hypotenuse of a right triangle, with legs of length \(\(|z|\) and \(|1-1| = 0\)\). By the Pythagorean theorem, we have \(\(|z-1|^2 = |z|^2 + |1-0|^2 = |z|^2\)\). Similarly, for the line segment connecting \(z\) and \(-1\), we have \(\(|z+1|^2 = |z|^2\)\). Therefore, we can rewrite the inequality as\(\(|z-1| + |z+1| = \sqrt{|z-1|^2} + \sqrt{|z+1|^2} = \sqrt{|z|^2} + \sqrt{|z|^2} = 2|z|\)\). Since \(\(|z| < 1\)\), it follows tha\(t \(2|z| < 2\)\), and therefore \(\(|z-1| + |z+1| < 2 \leq 2\sqrt{2}\)\).
Case 2: \(\(|z| = 1\)\)
In this case, the point \(\(z\)\) lies on the boundary of the unit circle. The line segments connecting \(\(z\)\) to \(\(1\)\) and are both radii of the circle and have length \(1\). Therefore, \(\(|z-1| + |z+1| = 1 + 1 = 2 \leq 2\sqrt{2}\)\).
In both cases, we have shown that \(\(|z-1| + |z+1| \leq 2\sqrt{2}\)\) when\(\(|z| \leq 1\).\)
Learn more about complex plane here:
https://brainly.com/question/33093682
#SPJ11
6th grade advanced / 7th grade khan acadamy

Answers
Answer:
Step-by-step explanation:
both A and B are equivalent
If you spun the spinner 1 time, what is the probability
it would land on a gray piece?

Answers
Answer:
3/8
Step-by-step explanation:
There are 4 black sections, 3 gray sections, and 1 white section.
This means that there are 8 in total.
3/8 of the squares are gray so that would be the answer.
Berto has $12 to put gas in his car. If gas costs $3.75 per gallon, which ordered pair relating number of gallons of gas, x, to the total cost of the gas, y, includes the greatest amount of gas Berto can buy?
(__,__ )
Answers
Answer:
If gas costs $3.75 per gallon and Berto has $12, then he can purchase 12/3.75 gallons. This is approximately 3.2 gallons. So the coordinate on this line would be (3.2, 12).
Actually... It's from web
A circle inscribed in a square and circumscribed about another square as shown. What is the ratio of the circle's shaded area to the area between the two squares
Answers
Answer: The ratio of the circle's shaded area to the area between the two squares is 0.1425 or 14.25%.The ratio of the circle's shaded area to the area between the two squares is given below. Inscribed circle in a square and circumscribed about another square:
The circle's diameter is equal to the length of the smaller square's side and is also equal to the longer square's diagonal. Let's suppose the length of the side of the smaller square is a units, then the diagonal will be a√2 units.
Now, the radius of the circle = diameter/2= a/2 units.
And the area of the circle=
c
The area of the smaller square = a² sq. units.
The area of the larger square = diagonal² =
\((a√2)² = 2a² sq. units\).
Area between the squares = (area of larger square) – (area of smaller square) =\(2a² – a² = a² sq.\) units.
Area of the shaded region = Area of the larger square – Area of the circle= \(2a² – πa²/4\)
Now, Ratio of the circle's shaded area to the area between the two squares is given by the formula:
Ratio = Area of the circle/Area between the squares=
\(πa²/4/2a² - a²/4= π/8 - 1/4= (3.14/8) - (1/4)= (0.3925 - 0.25)\)
Ratio = 0.1425 or 14.25%
To know more about circumscribed visit:-
https://brainly.com/question/11323000
#SPJ11
Solve this inequality
2x2 – 15x < 27
Answers
Find the greatest common factor for each problem.use the t-chart to slow?
16 and 40
Gcf:
Answers
The required GCF is 8.
The greatest common factor is that greatest number from the factors which divides the number completely.
For example take numbers 12 and 16.
The factors of 12 are 2×2×3.
And the factors of 16 are 2×2×2×2.
We can clearly see that the common factors are 2×2 which gives 4. So, 4 is the greatest common factor which divides both 12 and 16.
Here it is given to find the greatest common factor of 16 and 40.
Factors of 16 = 2×2×2×2
Factors of 40 = 2×2×2×5
We can see clearly the common factors are 2×2×2 which gives 8.
So, 8 is the greatest common factor.
To learn more about the factors visit the link :
https://brainly.com/question/24182713
#SPJ9
How many solutions are there for this equation? Why?
2(m+2)=12−6m
Answers
Answer:
Only one solution which is 1
Step-by-step explanation:
2m+4=12-6m (Distribute the 2 to m and 2)
8m+4=12 (Move the 6m to the other side)
8m=8 (move the 4 to the other side)
m=1 (There is only one answer which is 1)
Hope this helps
Diff of squares help me out
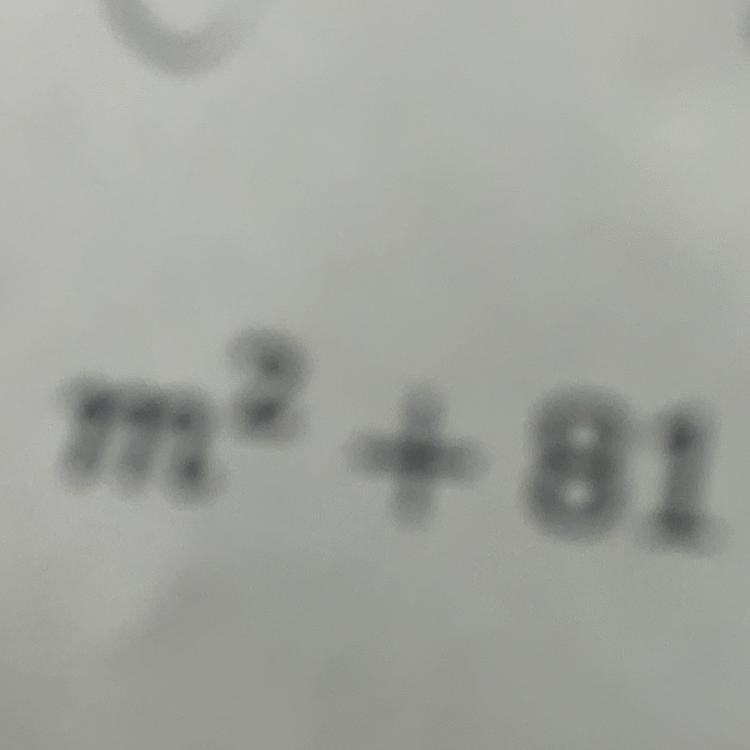
Answers
Answer:
9
Step-by-step explanation:
9 is the correct answer
I WILL MARK BRAINLIEST!
I had 3 times as many rose bushes as holly bushes in my garden. Then i moved seven of my rose bushes to my grandfather’s garden, and i planted 11 new holly bushes in my garden. Now there are 6 fewer rose bushes than holly bushes in my garden. How many rose bushes did I have initially?
Answers
Initially the number of rose bushes are 18 and number of holly bushes are 6.
What is linear equation?It is defined as the relation between two variables, if we plot the graph of the linear equation we will get a straight line.
If in the linear equation, one variable is present, then the equation is known as the linear equation in one variable.
Let's suppose initially the number of rose bushes is x and number of holly bushes is y
x = 3y …(1)
Then I moved seven of my rose bushes to my grandfather’s garden:
= (x - 7)
Planted 11 new holly bushes in my garden:
= (y + 11)
x - 7 = y + 11 - 6
x - y = 12 ...(2)
After solving equation (1) and (2):
x = 18
y = 6
Thus, initially the number of rose bushes are 18 and number of holly bushes are 6.
Learn more about the linear equation here:
brainly.com/question/11897796
#SPJ1
Using a unit circle, what are the degree measures of all angles with the given cosine?
-√3/2
Answers
Using the unit circle the degree measure giving cosθ = -√3/2, are θ = 150° and θ = 210°
What is a unit circle?A unit circle is a circle of radius one unit
In a unit circle, we have that
cosθ = xsinθ = yNow, using a unit circle, we desire to find what are the degree measures of all angles with the given cosine = -√3/2. We proceeed as follows.
Since cosθ = -√3/2, we know that cosine is negative in the second and theird quadrant.
So, we have that
cos(180° - θ) = √3/2 and cos(180° + θ) = √3/2
Taking inverse cosine of both sides, we have that
cos(180° - θ) = √3/2 and cos(180° + θ) = √3/2
180° - θ = cos(√3/2) and 180° + θ) = cos(√3/2)
180° - θ = 30° and 180° + θ = 30°
θ = 180° - 30° and θ = -180° + 30°
θ = 150° and θ = -150°
θ = 150° and θ = -150° + 360°
θ = 150° and θ = 210°
So, the degree measure are θ = 150° and θ = 210°
Learn more about unit circle here:
https://brainly.com/question/30372059
#SPJ1
Answer:
150° and 210°
Step-by-step explanation:
The unit circle is a circle with a radius of 1 unit, centered at the origin (0,0) in a coordinate plane. In the unit circle, the cosine of an angle is represented by the x-coordinate of the point on the circle corresponding to that angle.
To determine the degree measures of angles with a cosine of -√3/2, we can refer to the unit circle and identify the angles where the x-coordinate (cosine) is equal to -√3/2.
In the unit circle, there are two such points where the x-coordinate is equal to -√3/2:
\(\left(-\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right)\;\; \textsf{and}\;\;\left(-\dfrac{\sqrt{3}}{2},-\dfrac{1}{2}\right)\)
These points correspond to angles 150° and 210°.
