72 pointsWhat postulate or theorem can you use to prove the pair of triangles are congruent? Name the missing congruence statement.DCA ABC A type your answer...by type your answer...

Answers
The two triangles ABC and ACD have two sides with same length: AD and BC, and both have the side AC. They also have one equivalent angle.
Therefore, they are congruent by SAS property.
Answer:
\(\Delta ABC\cong\Delta CDA\text{ by }SAS\)Related Questions
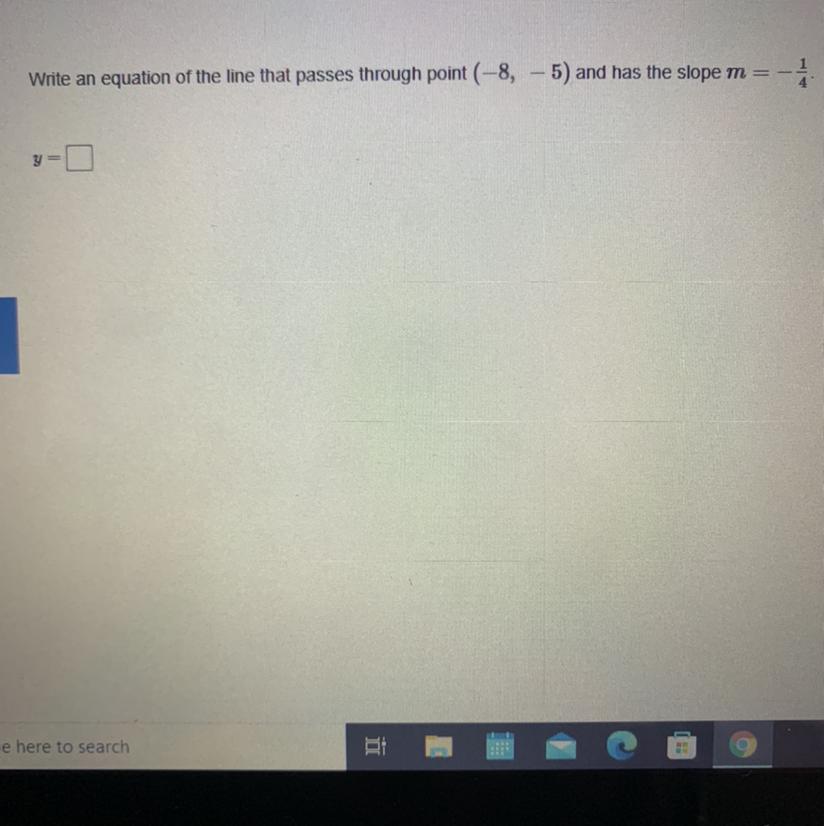
Write an equation of the line that passes through point (-8, – 5) and has the slope m= - 1/4
y=
Answers
Answer:
y= -1/4x + 3
Step-by-step explanation:
y-y1 = m(x-x1)
(-8 {x1}, -5 {y1}, -1/4 [m] )
We'll then replace the letters with the available figures.
y-[-5] = -1/4 (x-[-8])
We are made to know that minus + minus= plus
Minus + plus= Minus
Minus x minus = plus
minus x plus = minus
Therefore, the mathematical setting of this question becomes,
y+5 = -1/4 (x+8)
Multiply everything in the bracket with the outside value
-1/4 x X = -1/4x
-1/4 x 8 = -2
The mathematical setting then becomes,
y+5 = -1/4x + -2 (Note: plus + minus = minus)
so, it becomes
y+5 = -1/4x - 2
The equation is supposed to look like this, y= mx + b
Therefore we add +5 to both sides to cancel out
y+5 = -1/4x - 2
+5 +5
+5 cancels out +5 which makes the setting,
y= -1/4x - 2 +5 (-2+5 goes around to become 5-2= 3)
The expression now looks like this
y= -1/4x +3 which is the final answer!
\(y= -1/4x + 3\)
Nonstop trains leave Toronto and Montreal at the same time each day going to the other city along the main line. One train travels at 120 km/h and the other at 90 km/h. Assuming the track is straight, how far apart are they one hour before they meet?
pls help ( ˘︹˘ )
Answers
Assuming the track is straight, the distance at which they are apart one hour before they meet is; 30 km
How to find the distance from speed and time?We are told that a Nonstop trains leave Toronto and Montreal at the same time each day going to the other city along the main line.
Speed of Train 1 = 120 km/h
Speed of Train 2 = 90 km/h
Time spent by train 1 = 1 hour
Time spent train 2 = 1 hour
Formula for distance is;
Distance = Speed * time
If they leave the same time each day, it means that;
Distance of train 1 = 120 * 1 = 120 km
Distance of train 2 = 90 * 1 = 90 km
Thus, distance at which they will be apart before meeting each other is;
Distance apart = 120 - 90
Distance apart = 30 km
Read more about Distance, speed and time at; https://brainly.com/question/4931057
#SPJ1
13) through: (0, -1) and (-5,-1)
A) x + 3y = 3
B) x - 3y = 1
C) 5r - 3y = -3
D) y=-1
Answers
Answer:
y=-1
Step-by-step explanation:
m=(y2-y1)/(x2-x1)
m=(-1-(-1))/(-5-0)
m=(-1+1)/-5
m=0/-5
m=0
y-y1=m(x-x1)
y-(-1)=0(x-0)
y+1=0
y=0-1
y=-1
At a farmers market to vendors sell fresh milk. One vendor sells 2 L for $3.80, and another vendor sells 1.5 L for $2.70. Which leader is a better deal. SOME ONE PLEASE HELPPP
Answers
Answer:
The second dealer is better.
Step-by-step explanation:
3.8/2= 2.7/1.5=
3.8/2=1.9 (first vendor) 2.7/1.5=1.8 (second vendor) 1.8 is less than 1.9.
15
Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar.
What value of p makes the equation true?
–3p +1/8 = -1/4
p=
Reset
Next
Answers
Answer:
\(p=\frac{1}{8}\)
Step-by-step explanation:
\(-3p+\frac{1}{8}=-\frac{1}{4}\)
Subtract \(\frac{1}{8}\) from both sides:
\(-3p=-\frac{1}{4}-\frac{1}{8}\)
Multiply \(\frac{1}{4}\) by \(\frac{2}{2}\) and simplify:
\(-3p=-\frac{3}{8}\)
Divide both sides by -3:
\(p=\frac{3}{24}\)
Simplify:
\(p=\frac{1}{8}\)
Find the standard form for the TANGENT PLANE to the surface: : = f (x, y) = x cos (xy) at the point (1, , 0). (???) (x – 1) + (???) (y – . + (: – 0) = 0
Answers
The standard form of the tangent plane to the surface represented by the function f(x, y) = xcos(xy) at the point (1, α, 0) is (x - 1) + α(y - β) + (f(1, α) - 0) = 0.
To find the standard form of the tangent plane, we first need to calculate the partial derivatives of the function f(x, y) = xcos(xy) with respect to x and y.
∂f/∂x = cos(xy) - yxsin(xy)
∂f/∂y = -x^2sin(xy)
Next, we evaluate these partial derivatives at the given point (1, α, 0) to obtain their values.
∂f/∂x evaluated at (1, α, 0) = cos(0) - α(1)sin(0) = 1
∂f/∂y evaluated at (1, α, 0) = -(1)^2sin(0) = 0
Using the values of the partial derivatives and the given point, we can write the equation of the tangent plane in point-normal form:
(x - 1) + α(y - β) + (f(1, α) - 0) = 0
Here, α represents the y-coordinate of the given point (1, α, 0), β can be any constant, and f(1, α) is the value of the function at the point (1, α, 0).
Note that the values of ∂f/∂x and ∂f/∂y at the given point determine the coefficients of x and y in the equation of the tangent plane, respectively.
For more questions like Derivative click the link below:
https://brainly.com/question/25324584
#SPJ11
Type the correct answer in the box. Use numerals instead of words. If necessary, use/ for the fraction bar.
Given the figure, find the total area of the shaded region.
D
8-
6-
4-
2-
O
-2-
o
S
The area of the shaded region is
B
R
8
с
square units
Answers
The value of the total area of the shaded region are,
⇒ 42 units²
We have to given that;
Sides of rectangle are,
AB = 9
BC = 6
Hence, The area of rectangle is,
⇒ 9 x 6
⇒ 54 units²
And, Area of triangle is,
A = 1/2 × 4 × 6
A = 12 units²
Thus, The value of the total area of the shaded region are,
⇒ 54 - 12
⇒ 42 units²
So, The value of the total area of the shaded region are,
⇒ 42 units²
Learn more about the rectangle visit:
https://brainly.com/question/2607596
#SPJ1

Express the product of ( 1/4x−6 ) and ( 4/3x-5/4 ) as a trinomial in simplest form.
Answers
\(( \frac{1}{4} x - 6)( \frac{4}{3} x - \frac{5}{4} )\)
\( \frac{1}{4} x( \frac{4}{3} x - \frac{5}{4} ) - 6( \frac{4}{3} x - \frac{5}{4} )\)
\( \frac{4}{12} {x}^{2} - \frac{5}{16} - \frac{24}{3} x - \frac{30}{4} \)
\(\frac{1}{3} {x}^{2} - \frac{5}{16} - 8x - \frac{30}{4} \)
\( \frac{1}{3x {}^{2} } - 8x - ( \frac{5}{16} + \frac{120}{16} )\)
\( \frac{1}{3x {}^{2} } - 8x - \frac{125}{16} \)
6x 2 y
6d - 2d +3e
5 x h
Answers
Answer:
install mo po yan na app,

wanda summers teaches 10th grade english. if she is paid a weekly salary of $750.00 what is her annual salary
Answers
Answer: 39,000 dollars
Step-by-step explanation: weekly salary multiplied by how many weeks are in a year(52)
i roll a die n times, n∈ℕ. find the probability that numbers 1 and 6 are both observed at least once.
Answers
The probability of both 1 and 6 being observed at least once when rolling a die n times is given by P(A ∪ B), which is equal to 1 - (11/6)^n + (2/3)^n.
To find the probability that numbers 1 and 6 are both observed at least once when rolling a die n times, we can use the principle of inclusion-exclusion.
Let A be the event that 1 is not observed in n rolls, and B be the event that 6 is not observed in n rolls.
Then, the probability of A and B not occurring is (5/6)^n and the probability of their union, denoted by A ∪ B, is 1 - (5/6)^n.
However, this includes cases where neither 1 nor 6 are observed at least once. To exclude these cases, we can use the same principle to count the number of ways in which neither 1 nor 6 are observed and subtract it from the total number of possible outcomes, which is \(6^n\).
Let C be the event that neither 1 nor 6 are observed in n rolls. Then, the probability of C occurring is (4/6)^n = (2/3)^n. By inclusion-exclusion, the probability of both 1 and 6 being observed at least once in n rolls is:
P(A ∪ B) = 1 - (5/6)^n - (5/6)^n + (2/3)^n
Simplifying this expression gives:
P(A ∪ B) = 1 - (11/6)^n + (2/3)^n
Therefore, there are 1 - (11/6)^n + (2/3)^n probability that numbers 1 and 6 are both observed at least once.
To know more about principle of inclusion-exclusion refer here:
https://brainly.com/question/32097111#
#SPJ11
Write an equation in point-slope form of the line that passes through the point (-8,-2) and has a slope of m=5.
Answers
Answer:
y+2=5(x+8)
Step-by-step explanation:
y-y1=m(x-x1)
plug the coordinate and slope in...
y+2=5(x+8)
DONE
Answer:
try y=5x-42
Step-by-step explanation:
Help please...........

Answers
Answer:
18
Step-by-step explanation:
3 x 6=18
what is the null hypothesis of the dickey-fuller test 1? the series is stationary around a 0 mean the series is stationary around a non 0 mean the series is non-stationary and has 0 mean the series is non-stationary and has a non 0 mean
Answers
If you have a trend then the process is non-stationary, but if you account for the time trend, it's still stationary around the line.
What is Null hypothesis?
The null hypothesis in inferential statistics is that two possibilities are equal. The underlying assumption is that the observed difference is just the result of chance. It is feasible to determine the probability that the null hypothesis is correct using statistical testing.
Consider the given process:
\(x_{t} = c+\alpha x_{t-1}+\beta _{t} \\E[\beta _{t}]=0\\\)
Obtain mean,
\(E[x _{t}]=\frac{c}{1-\alpha }\)
This works only when |α|<1. If α=1 this doesn't work, it blows up, because , \(E[x _{t}]\neq E[x _{t-1}]\) i.e. the process is not stationary.
The constant refers to the term c.
The trend is easy too:
\(x_{t} +c+\alpha t+\alpha x_{t-1} +\beta_{t}\)
In this case,
\(E[x _{t}]=\frac{c+\alpha t}{1-\alpha }\)
So, if you have a trend then the process is non-stationary, but if you account for the time trend, it's still stationary around the line.
To know more about Null hypothesis visit,
https://brainly.com/question/25263462
#SPJ4
PLEASE HELP!!!
The population of a town increases by 3% each year. If its population today is 25,000, what will its population be in 5 years?
A 25,000 (1.03)
B 25,000-(1.03)5
25,000-(0.03)
25,000 (1.03) - (5)
Answers
The population of the town in 5 years will be approximately 28,982.
What is exponential growth?A data pattern known as exponential growth exhibits faster expansion over time. Compounding generates exponential profits in finance. Exponential growth is possible in savings accounts with a compounding interest rate. Compound returns in finance lead to exponential development. One of the most potent forces in finance is the power of compounding. With the help of this idea, investors may generate sizable sums with little start-up money. Compound interest savings accounts are typical instances of exponential development.
Given that, population of a town increases by 3% each year.
The population after 5 years is calculated by:
Population in 5 years = Initial population x (1 + rate) raised to time.
That is,
Population in 5 years = 25,000 x (1 + 0.03)⁵
Population in 5 years = 25,000 x 1.159274
Population in 5 years = 28,981.85
Hence, the population of the town in 5 years will be approximately 28,982.
Learn more about exponential growth here:
https://brainly.com/question/11487261
#SPJ1
Pythagorean Theorem can be done on any three sided triangle?
Answers
Answer: No, the pythagorean Theorem can only be done on right triangles.
Step-by-step explanation:
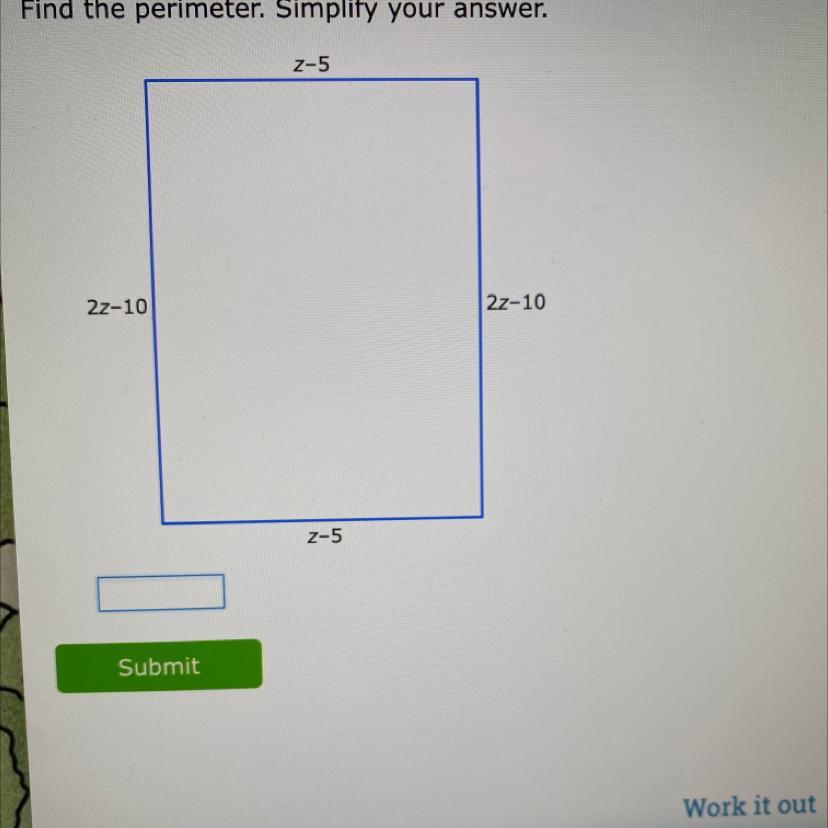
Find the perimeter. Simplify your answer.
Answers
Answer:
6z-30 :D
Step-by-step explanation:
Step-by-step explanation:
The perimeter of a square is just all the sides added up together. To do this we can make an equation.
2(z-5) + 2(2z - 10)
This represents two sides with different lengths two times. To solve, you first use the distributive property to multiply z-5 by 2.
2z - 10 + 2(2z - 10)
We then use the distributive property by multiplying 2z - 10 by 2.
2z − 10 + 4z − 20
We then combine 2z and 4z to get 6z.
6z − 10 − 20
Subtract 20 from 10 to get -30.
6z-30.
pls help whats 4/5 of 30?
I'll give brainliest:)
Answers
Answer:
24
Step-by-step explanation:
yur welcome
An object located 1.03 cm in front of a spherical mirror forms an image located 11.6 cm behind the mirror. (a) What is the mirror's radius of curvature (in cm)? cm (b) What is the magnification of the image?
Answers
The radius of curvature (r) is -100 cm and Magnification (m) is 11.26. The mirror is a concave mirror.
Given Data: Object distance, u = -1.03 cm; Image distance, v = 11.6 cm
To find: The radius of curvature (r) and Magnification (m).
Formula used:
1/f = 1/v - 1/u;
Magnification, m = -v/u
Calculation:
Using the formula,
1/f = 1/v - 1/u
1/f = 1/11.6 - 1/-1.03 = -0.02
f = -50 cm
The radius of curvature,
r = 2f
r = 2 × (-50) = -100 cm
Since the radius of curvature is negative, the mirror is a concave mirror.
Magnification, m = -v/u= -11.6/-1.03= 11.26
Hence, the radius of curvature (r) is -100 cm and Magnification (m) is 11.26.
Learn more about magnification visit:
brainly.com/question/21370207
#SPJ11
In 2004 there were 7,000000 people living alone in great Britain this is four time as many as in 1961, Calculate how many people lived alone in 1961. Express your answer in standard form
Answers
Answer:
1.75 × 10⁶
Step-by-step explanation:
7,000,000 ÷ 4 = 1750000
Which is 1.75 × 10⁶ in standard form
5
A trapezium has an area of 36 cm². The two parallel sides are 3 cm and 6 cm.
Find the distance between the two parallel sides.
Answers
The distance between the two parallel sides of the trapezium is 8 cm.
What is the height of the trapezium?A trapezium is a convex quadrilateral with exactly one pair of opposite sides parallel to each other.
The area of a trapezium is expressed as:
Area = 1/2 × ( a + b ) × h
Where a and b are base a and base b, h is height.
Given that:
Area of the trapezium = 36 cm²
Base a = 3 cm
Base b = 6 cm
Height h =?
Plug the given values into the above formula and solve for height:
Area = 1/2 × ( a + b ) × h
36 = 1/2 × ( 3 + 6 ) × h
36 = 1/2 × ( 9 ) × h
36 = 4.5 × h
h = 36 / 4.5
h = 8 cm
Therefore, the height of the trapezium is 8 cm.
Learn more about trapeziums here: https://brainly.com/question/22607187
#SPJ1
what is the GCF of 9a4b4-27a3b3?
Answers
Answer:
9a³b³
Step-by-step explanation:
9a³b³(ab - 3) = 9a^4b^4 - 27a^3b^3
Answer:
9a^3 b^3
Step-by-step explanation:
GCF=Greatest common factor
Huda evaluated the expression below.
Negative 3 (8 minus 5) squared minus (negative 7) = negative 3 (3) squared minus (negative 7) = -3 (9) minus (-7) = 27 - (-7) = 34.
What was Huda’s error?
A. Huda evaluated (3) squared incorrectly.
B. Huda found the product of –3 and 9 as positive.
C. Huda subtracted –7 from 27 incorrectly.
D. Huda did not follow the order of operations.
Answers
Answer:
b Huda found the product of –3 and 9 as positive.
yeah-
will give brainliest to the correct answer (no links or account will be reported) :)

Answers
Answer:
122
Step-by-step explanation:
64 + 58 = (l)
(l) = 122
an atomic absorption method for determination of copper in fuel samples yielded a pooled standard deviation of (). how many replicate measurements are necessary to decrease the 95 and 99% confidence limits to ?
Answers
Replicate measurements of 14 and 33 are necessary to decrease the 95 and 99% confidence limits to +0.19ug Cu/mL respectively.
a) For a 95% confidence limit, N is about 14
b) For a 99% confidence limit, N is about 33
To determine the number of replicate measurements necessary to achieve a desired confidence limit, we can use the formula:
\(N = (z * Spooled / d)^2\)
where z is the Z-score associated with the desired confidence level (from the table provided), Spooled is the pooled standard deviation, and d is the desired decrease in the confidence limit.
For a 95% confidence level, z = 1.96. Substituting the given values into the formula, we get:\(N = (1.96 * 0.27 / 0.19)^2 = 14.22 = 14\) (rounded to the nearest integer)
For a 99% confidence level, z = 2.58. Substituting the given values into the formula, we get:\(N = (2.58 * 0.27 / 0.19)^2 = 33.06 = 33\) (rounded to the nearest integer)
Learn more about Atomic absorption method here:
https://brainly.com/question/28697356
#SPJ4
Complete Question:
An atomic absorption method for the determination of copper in fuel samples yielded a pooled standard deviation of Spooled = 0.27ug Cu/mL (s-->Sigma). How many replicate measurements are necessary to decrease the 95 and 99% confidence limits to +0.19ug Cu/mL?
Confidence Level%/z 95%/1.96 99%/2.58
a) For a 95% confidence limit, N is about __?
b) For a 99% confidence limit, N is about __?
A store pays $10 for a blanket. The markup is 35%. What do they sell it for?
Answers
Explanation:
35% = 0.35
$10 = 100%
135% * 10 = 1.35 * 10 = 13.5
35% markup of $10 equals $13.50
PLEASE HELP ASAP! 100 PTS *TRIGONOMETRY*
1. Find the measure of the side indicated (x). Round to the nearest tenth. Show your work to support your answer. (First Picture)
2. Find the measure of the angle indicated (x). Round to the nearest tenth. Show your work to support your answer. (Second Picture)


Answers
1:
cos (37)= 11/x
x(cos(37))= 11
x= 11/cos(37)
x= 14.4
2:
tan (0)= 4/13
0= tan^-1/ 4/13
0= 0.3
x= 0.3
have a nice day :)Step-by-step explanation:
solution:
A.
relation between hypotenuse and base is given by cos angle
so
\( \cos(ø) \)=base/hypotenuse=11/x
cos37°=11/x
x=11/(cos37°)=13.77units
side indicated =x=13.77units
solution:
B.
relation between perpendicular and base is given by tan angle
so
\( \tan(ø) \)=perpendicular/base=4/13
ø=tan-¹ (4/13)=17.10°
angle indicated =ø=17.10°
is 7.69 x 24^8 in scientific notation
Answers
Reason:
The 24 needs to be changed to a 10 for it to be in scientific notation.
The template for scientific notation is \(a * 10^b\) where \(0 \le |a| < 10\)
So for example, \(1.23 \times 10^4\) is in scientific notation.
what is the shift
y = log(x+4) -3
Answers
The shift of the function y = log(x+4) -3 is 4 units left and 3 units down
How to determine the shiftFrom the question, we have the following parameters that can be used in our computation:
y = log(x + 4)
The above equation is a logarithmic equation
So, the parent function is
y = log(x)
When the parent function is compared to the given function, we have
3 units down and 4 units left
Read more about transformation at
https://brainly.com/question/1548871
#SPJ1
PLEASE HELP IF POSSIBLE :)

Answers
Answer: 2cm
Step-by-step explanation: