7) Paul is designing a flower garden. If he makes
the garden 21 feet long and 2.5 foot wide, what
will the area of the garden bo?
Answers
Answer:
52.5 feet
Step-by-step explanation:
The area of a square is length * width
Since both length and width are given to us in the equation, we can just plug them into our equation
21 * 2.5 = 52.5
Best of luck
Related Questions
What are the solutions to logs (x²+8)= 1+logg(x)?
x=-2 and x=-4
x-1 and x=8
x= 1 and x = -8
O x=2 and x=4
Answers
Step-by-step explanation:
Log(x²+8)=log 10+ log x
Log(x²+8)=log(10×x)
x²+8=10x
x² - 10x + 8=0
x is approximately to - 1 and - 8✅
The solutions to the given equation are x = -1 and x = 8.
Option A is the correct answer.
What is a solution?Solutions are the values of an equation where the values are substituted in the variables of the equation and make the equality in the equation true.
We also find the solution in a system of equations using the substitution or elimination method.
Example:
2x + 4 = 8
The solution is x = 2.
We have,
Using logarithmic properties, we can simplify the given equation:
logs(x² + 8) = 1 + log g(x)
logs(x² + 8) - log g(x) = 1
log[(x² + 8)/g(x)] = 1
(x² + 8)/g(x) = 10
x² + 8 = 10g(x)
Now we can solve for x by substituting the given answer options and solving for g(x):
For x = -2 and x = -4:
x = -2:
(-2)² + 8 = 12, which is not equal to 10 g(x) for any value of g(x).
So x = -2 is not a solution.
x = -4:
(-4)² + 8 = 24, which is also not equal to 10g(x) for any value of g(x).
So x = -4 is not a solution.
For x = -1 and x = 8:
x = -1:
(-1)² + 8 = 9, which is equal to 10g(x) when g(x) = 0.9.
So x = -1 is a solution.
x = 8:
(8)² + 8 = 72, which is equal to 10g(x) when g(x) = 7.2.
So x = 8 is a solution.
For x = 1 and x = -8:
x = 1:
(1)² + 8 = 9, which is equal to 10g(x) when g(x) = 0.9.
So x = 1 is a solution.
x = -8:
(-8)² + 8 = 56, which is not equal to 10g(x) for any value of g(x).
So x = -8 is not a solution.
Therefore,
The solutions to the given equation are x = -1 and x = 8.
Learn more about solutions of equations here:
https://brainly.com/question/545403
#SPJ5
5h-6-8+7h what’s the answer ?
Answers
You have 2. 5 m of rope and cut 11. 5 inch pieces. How many centimeters of rope will be left over?.
Answers
Answer: 16.3 cm
Step-by-step explanation:
2.5 meters = 98.4252 inches.
(Round to 98.4)
98.4 - 11.5 = 86.9
(keep subtracting till you can't subtract 11.5 anymore w/o getting a negative number)
6.4 in = 16.3 cm (multiply the length value by 2.54)
16.3 cm left over.
solve that please
show all work

Answers
Answer:
There is not enough information to find a solution. The work to find it if more variable are filled is below. You can also solve the problem by inputting these equations as solutions.
Step-by-step explanation:
(x^(2)+a)(x^(2)-b)=0
You can find x by taking the square root of both sides
√(-a), -√(-a), √b, -√b
You can find a by -x^(2)
You can find b by x^(2)
Mystery Number:
I round to 375,400 when
rounded to the nearest hundred
have an odd hundreds digit,
tens digit, and ones digit
My tens and ones digits are
the same and both less than 7
What number am I?

Answers
Answer:
Step-by-step explanation:
375355
The three steps below were used to find the value of the expression [(-10 + 2) - 1] + (2 + 3). Step 1: ? Step 2: -9 + 2 + 3 Step 3: -7 + 3 Which expression is missing from Step 1? Question 3 options: [-10 + -1 + 2] + (2 + 3) [-8 - 1] + (2 + 3) [-10 + 1] + (2 + 3) [8 + 1] + (2 + 3)
Answers
Therefore, the missing expression in Step 1 is [-8 - 1] + (2 + 3).
In order to find the missing expression in Step 1, let's analyze the given steps and the final expression.
Step 1: ?
Step 2: -9 + 2 + 3
Step 3: -7 + 3
To find the missing expression in Step 1, we need to work backwards from Step 3 to Step 1.
In Step 3, the expression "-7 + 3" gives us a result of -4.
In Step 2, the expression "-9 + 2 + 3" gives us a result of -4.
So, the missing expression in Step 1 should also evaluate to -4 when performed correctly.
Let's check the available options:
[-10 + -1 + 2] + (2 + 3) = -11 + 2 + 5 = -4
[-8 - 1] + (2 + 3) = -9 + 5 = -4
[-10 + 1] + (2 + 3) = -9 + 5 = -4
[8 + 1] + (2 + 3) = 9 + 5 = 14
Out of the given options, only option 2, [-8 - 1] + (2 + 3), correctly evaluates to -4. Therefore, the missing expression in Step 1 is [-8 - 1] + (2 + 3).
For more questions on missing expression
https://brainly.com/question/14581389
#SPJ8
Which equations are correct?
Select each correct answer.

Answers
Solve for \(y\) as a function of \(x\):
\(\frac{dy}{dx}=2xy^3\sin\left(x^2\right)\) and \(y(0)=-1\)
Answers
The solution to the differential equation dy / dx = 2 · x · y³ · sin x² is equal to - [1 / (2 · y²)] = - cos x² - 3 / 2.
How to solve a separable variable differential equation
In this problem we find a differential equation with separable variables, that is, an ordinary differential equation whose variables can be separated on each side of the equivalence and solved by integrals. First, write the complete expression:
dy / dx = 2 · x · y³ · sin x²
Second, separate the variables:
dy / y³ = 2 · x · sin x² dx
Third, integrate the equation:
∫ dy / y³ = ∫ sin x² · (2 · x) dx
- [1 / (2 · y²)] = - cos x² + C
Fourth, find the value of the constant of integration:
- 1 / 2 = 1 + C
C = - 3 / 2
Fifth, write the solution to the differential equation:
- [1 / (2 · y²)] = - cos x² - 3 / 2
To learn more on differential equations: https://brainly.com/question/2273154
#SPJ1
Two find the point in the solution set for both these functions equation the two functions (f(x)=g(x)) and solve for x. See full process below.
Explanation:
Two find the point in the solution set for both these functions equation the two functions (f(x)=g(x)) and solve for x.
Therefore:
2x−1=−43x+9
We can now solve for x:
2x−1+43x+1=−43x+9+43x+1
2x+43x−1+1=−43x+43x+9+1
2x+43x−0=0+9+1
2x+43x=10
(33×2)x+43x=10
63x+43x=10
103x=10
310×103x=310×10
3
10×103x=310×10
x=3 is the point which lies in the solution set for both functions.
Please answer this correctly without making mistakes

Answers
Answer:
I say first one 7-pint jug of water for 3.22
Step-by-step explanation:
because 8 pints are in 1 gallon but there is 7 pints for 3.22 if do math correctly 8 pints would be 3.68 and that is one gallon right there so 2 gallons would only be 7.36 which is way cheaper than the second one being 2-gallon jug of water for 13.44.
hope this helps.
The Point (0,0) is a solution to which of these inequalities?

Answers
Answer:
(0, 0) s the solution of y-4 < 3x-1 as it satisfies the inequality.
Hence, option C is true.
Step-by-step explanation:
Given the point (0, 0)
a)
Putting the point (0, 0) the inequality
y+4 < 3x-1
0+4 < 3(0)-1
4 < -1
This is false as -1 can not be greater than 4
b)
y-1 < 3x-4
Putting the point (0, 0) the inequality
0-1 < 3(0)-4
-1 < -4
This is false as -1 can not be lesser than -4
c)
y-4 < 3x-1
Putting the point (0, 0) the inequality
0-4 < 3(0)-1
-4 < -1
This is true as -4 is lesser than -1
d)
y+4 < 3x+1
Putting the point (0, 0) the inequality
0+4 < 3(0)+1
4 < 1
This is false as 4 can not be lesser than 1
Therefore, (0, 0) s the solution of y-4 < 3x-1 as it satisfies the inequality.
Hence, option C is true.
Please answer this correctly

Answers
The curve above is the graph of a sinusoidal function. It goes through the points
and
. Find a sinusoidal function that matches the given graph. If needed, you can enter
=3.1416... as 'pi' in your answer, otherwise use at least 3 decimal digits.

Answers
The sinusoidal function that matches the specified graph, expressed using π ≈ 3.1416 is; y ≈ 4·sin(0.628·(x + 3))
What is a sinusoidal function?A sinusoidal function is a periodic function that is based on either the sine or the cosine function.
The general form of a sinusoidal function is; y = A·cos(B·(x - C)) + D
The peak and the trough of the graph of the function indicates that the amplitude, A = (4 - (-4))/2 = 4
The vertical shift, D = (4 + (-4))/2 = 0
The period, P = 2·π/B
A cycle is completed in -0.5 - (-10.5) = 10 units of the x-value interval
P = 10 = 2·π/B
Therefore; B = π/5
When x = -8, y = 0, therefore;
0 = 4·sin((π/5)·((-8) - C)) + 0
4·sin((π/5)·((-8) - C)) = 0
sin((π/5)·((-8) - C)) = 0
(π/5)·((-8) - C) = 0
((-8) - C) = 0
C = -8
When x = 2, y = 0, therefore;
0 = 4·sin((π/5)·(2 - C)) + 0
4·sin((π/5)·(2 - C)) = 0
sin((π/5)·(2 - C)) = 0
(π/5)·(2 - C) = 0
(2 - C) = 0
C = 2
Similarly; When x = -3, y = 0, therefore; C = -3
y = 4·sin((π/5)·(x + 3))
The value C = -3, corresponds to the horizontal shift of the graph of the sine function, which is shifted 3 units to the left
The sinusoidal function, where π ≈ 3.1416 is therefore;
y ≈ 4·sin((0.628)·(x + 3))
Learn more on sinusoidal functions here: https://brainly.com/question/29529184
#SPJ1
plez halppp mehh ;-;

Answers
2) True
3) True.
You can see for number one the angles are not the same, therefore they are not equal to eachother.
For two, because the line EC is running flat it is equal to 180. Because their is a little box on the other side of 1 & 2, we know that is equivalent to 90 degrees. Therefore the other side (1 &2) HAS to be 90, because the line in which they are on is 180, 90+ 90 = 180.
3, The same type of math for #2
Answer:
False
True
True
Step-by-step explanation:
Angle 1 cannot be equal to angle 4. Even by just viewing one can see that they can't be equal.
Angle 1 and 2 when combined give a 90 degree angle going from a to c.
Angle 3 and 4 form a 180 degree angle.
HOPE THIS HELPED
$500 is invested in an account earning 7% interest compounded quarterly. Find the value
after 8 years.
Answers
The amount of the investment after 8 years will be, $4,357.64
Given, $500 is invested in an account earning 7% interest compounded quarterly.
We have to find the value of the invested amount after 8 years,
as, Amount = P(1 + r/100)^t
where, P is the amount of money invested, r is the rate of interest and t is the amount of time
Amount = 500(1 + 7/100)^(8×4)
Amount = 500(1.07)^32
Amount = 500×8.715
Amount = 4,357.635
So, the amount of the investment after 8 years will be, $4,357.64
Hence, the amount of the investment after 8 years will be, $4,357.64
Learn more about Compound Interest here https://brainly.com/question/24274034
#SPJ9
QUESTION 6 1 POINT
Using the table, what is the average daily balance of the credit card for the August 1 through August 31 billing period?
Round your answer to the nearest dollar.
Provide your answer below:
Day
1
8
16
24
Activity
Payment
Purchase
Purchase
Adjustment Closing Balance
-550
4
+200
+150
850
300
500
650
Answers
Rounded to the nearest dollar, the average daily balance of the credit card for the August 1 through August 31 billing period is $74.
To find the average daily balance of the credit card for the August 1 through August 31 billing period, we need to calculate the sum of the daily balances and divide it by the number of days in the billing period.
Let's calculate the daily balances for each day:
Day 1: Closing Balance = $850
Day 8: Closing Balance = $300
Day 16: Closing Balance = $500
Day 24: Closing Balance = $650
To calculate the daily balances, we need to consider the activities that occurred on each day.
On Day 1, there was no activity recorded, so the closing balance remains at $850.
On Day 8, a payment of $550 was made. Therefore, the closing balance is $850 - $550 = $300.
On Day 16, a purchase of $200 was made. Therefore, the closing balance is $300 + $200 = $500.
On Day 24, a purchase of $150 was made and an adjustment of $4 was applied. Therefore, the closing balance is $500 + $150 - $4 = $650.
Now, let's calculate the average daily balance:
Sum of daily balances = $850 + $300 + $500 + $650 = $2300
Number of days in the billing period = 31
Average daily balance = Sum of daily balances / Number of days = $2300 / 31 ≈ $74.19
For more such questions on balance
https://brainly.com/question/11070711
#SPJ8
M is the centroid of the triangle.
CM=7, PM=10, & BQ=18
RM=[?]
![M is the centroid of the triangle.CM=7, PM=10, & BQ=18RM=[?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/xZOATToGyX8TFczt2vK9eAUMQHkw8QIE.png)
Answers
Answer:
14
Step-by-step explanation:
As you can see the median containing RM is RC. Which means that RM=CM x 2
CM = 7
RM = 2*7 = 14
The length of RM from the given triangle PQR is 14 units.
What is centroid of a triangle?The point in which the three medians of the triangle intersect is known as the centroid of a triangle. It is also defined as the point of intersection of all the three medians.
Given that, M is the centroid of the triangle.
CM=7, PM=10 and BQ=18.
The centroid divides each median into two parts, which are always in the ratio 2:1.
So, RM:CM
RM:7
= 14:7
Therefore, the length of RM is 14 units.
Learn more about the centroid here:
brainly.com/question/10708357.
#SPJ2
A boy starts the week with 3kg of rice, every day he cooks 0.6kg. How much rice will he have left after 4 days?
Answers
Answer:
0.6kg
Step-by-step explanation:
working out how much rice has been used in 4 days:
0.6kg × 4 = 2.4kg
rice left over after 4 days:
3kg - 2.4kg = 0.6kg
Question 4 of 10
Solve the system of equations below by graphing both equations with a pencil
and paper. What is the solution?
y = x+ 5
y=-2x-1
A. (-2, -1)
B. (0,5)
C. (0, -1)
D. (-2,3)
SUBMIT
Answers
\(\\ \rm\Rrightarrow x+5=-2x-1\)
\(\\ \rm\Rrightarrow 3x=-6\)
\(\\ \rm\Rrightarrow x=-2\)
Put in 1st equation\(\\ \rm\Rrightarrow y=-2+5=-3\)
Option D is correct
Question Progress
Homework Progress
97
The ratio 60:48 in its simplest form is
Answers
It is with great pleasure that I am here to celebrate another year of my life , happy birthday to me#jackenleyjackenley

Answers
Step-by-step explanation:
Many many happy returns of the day.
May god give U a long life and success in your life.❤️❤️❤️❤️❤️❤️❤️❤️❤️
the school lisa goes to is selling tickets to the annual talent show. on the first day of ticket sales the school sold 4 senior citizen tickets and 5 student tickets for a total of $102. the school took in $126 on the second day by selling 7 senior citizen tickets and 5 student tickets. what is the price of on senior citizen ticket and one student ticket?
Answers
Answer: one senior ticket is $8 and one student ticket is $14
Hope this helps a little
Please help with this one I need it

Answers
Answer:
∠ BCA = 25°
Step-by-step explanation:
the inscribed angle BCA is half the measure of the central angle BOA , so
∠ BCA = \(\frac{1}{2}\) × 50° = 25°
2. Aimee lives 4/5 of a mile from
the park. She has walked 2/3 of
the way to the park. How far has
Aimee walked?
Answers
Answer:
\(\frac{8}{15}\) of a mile
Step-by-step explanation:
To find a segment of a fraction, you must first find the LCM of each value's denominator:
LCM - Lowest Common Multiple
The lowest common multiple is the number that shows up first in each number's multiple set.
Example: LCM of 4 and 6
Multiples of 4: 4, 8, 12, 16, 20
Multiples of 6: 6, 12, 18, 24, 30
Because 12 is the first number to show up in each multiple set, 12 is the LCM.
So, to be able to solve this problem easy, do the same with 5 and 3:
5, 10, 15, 20, 25
3, 6, 9, 12, 15
Since 15 is the first number in both sets, 15 is the LCM.
The next step is to multiply \(\frac{4}{5}\) by \(\frac{x}{x}\), x being the value that can be multiplied with the denominator to equal 15:
\(\frac{4}{5}\) × \(\frac{3}{3}\) = \(\frac{12}{15}\)
To find how much \(\frac{2}{3}\) of \(\frac{12}{15}\) is, multiply the fractions together:
\(\frac{12}{15}\) × \(\frac{2}{3}\) = \(\frac{24}{45}\)
Simplify the fraction by dividing the numerator and denominator by 3.
\(\frac{24}{45}\) ÷ \(\frac{3}{3}\) = \(\frac{8}{15}\)
Because the fraction can't be simplified any further, Aimee has walked a total of \(\frac{8}{15}\) of a mile.
can someone help me with this?

Answers
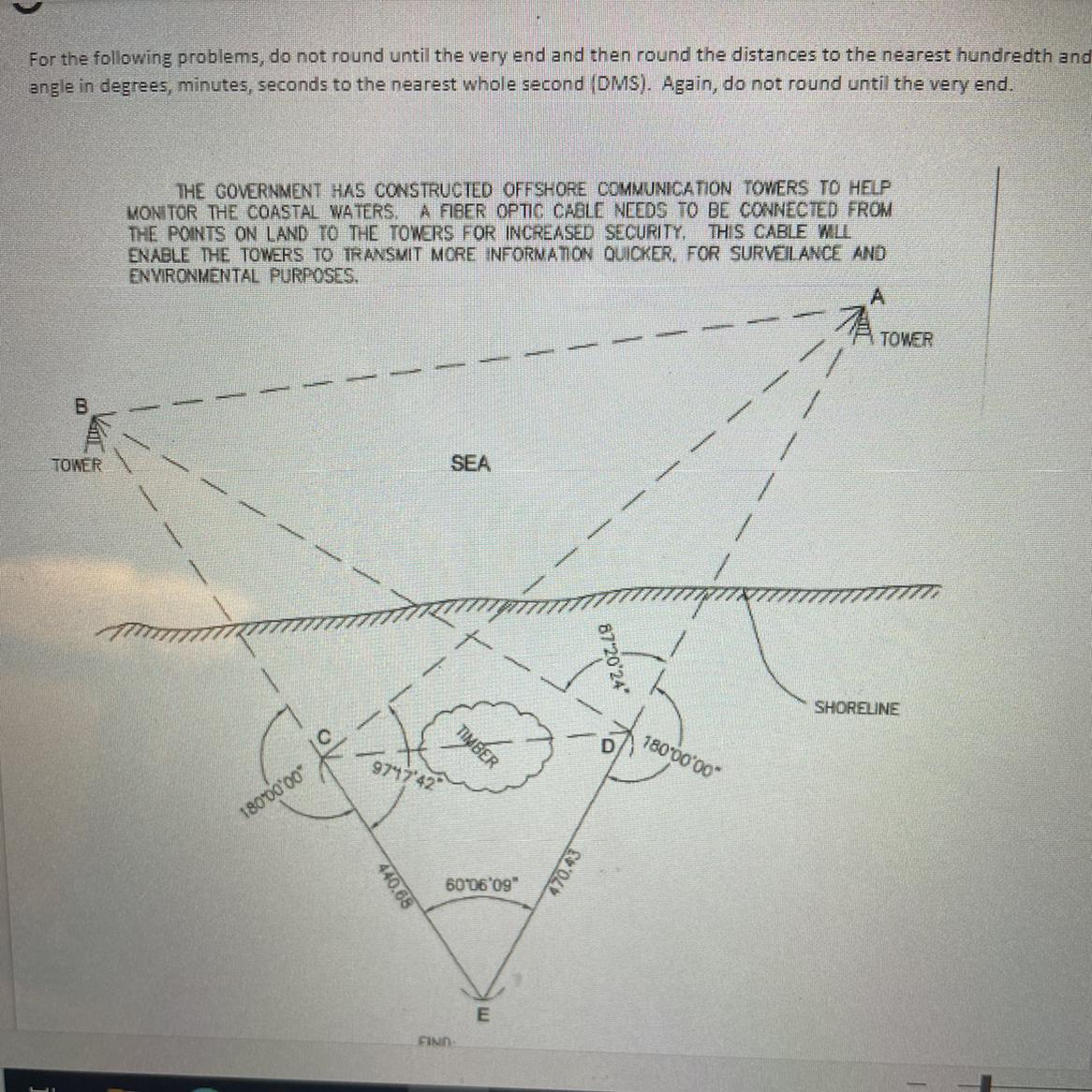
Hi I need help solving for each of the sides in this equation.CDABSolve to the nearest hundredth
Answers
Length of CD
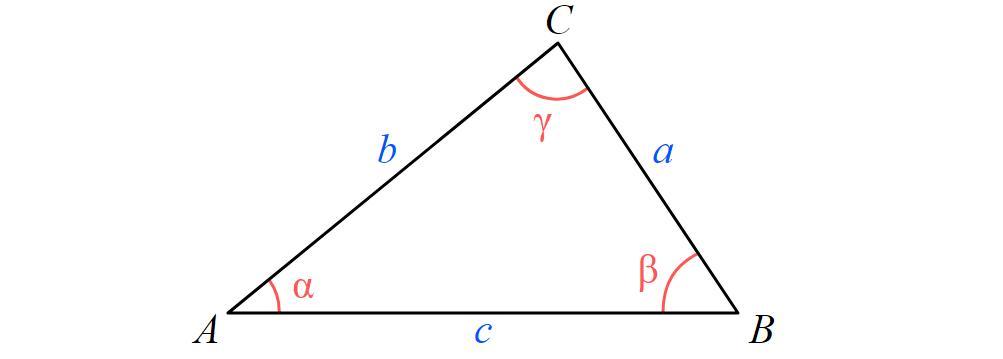
From the picture, we know two sides and an angle of the triangle CDE. We define the sides and angle:
• a = EC = 440.68,
,• b = ED = 470.43,
,• c = CD = ?,
,• γ = 60° 06' 09''.
From trigonometry, we know that the Law of Cosines states that:
\(\begin{gathered} c^2=a^2+b^2-2ab\cdot\cos\gamma, \\ c=\sqrt{a^2+b^2-2ab\cdot\cos\gamma}. \end{gathered}\)Where the angle γ and the sides a, b and c are defined by:
Replacing the values from above in the equation for side c, we get:
\(c=\sqrt{(440.68)^2+(470.43)^2-2\cdot440.68\cdot470.43\cdot\cos(60\degree06^{\prime}09^{\prime}^{\prime})}\cong457.10.\)Length of AB
To compute the length of AB, first, we must compute the length of sides AE and EB.
Side EB
From the picture, we see a triangle ECA. Using the data of the picture, we have:
• EC = 440.68,
,• ∠E = 60° 06' 09'',
,• EA = ?,
,• ∠A = ?.
,• ∠C = 97° 17' 42''.
Angles ∠A, ∠E and ∠C are the inner angles of triangle ECA, so they must sum up 180°, so we have:
\(\begin{gathered} ∠A+∠E+∠C=180\degree, \\ ∠A=180\degree-∠E-∠C, \\ ∠A=180\degree-60\degree06^{\prime}09^{\prime\prime}-97\degree17^{\prime}42^{\prime\prime}=22°36^{\prime}9^{\prime\prime}. \end{gathered}\)Now, we define the following sides and angles:
• c' = EC = 440.68,
,• γ' = ∠A = 22° 36' 9''
,• a' = EA = ?,
,• α = ∠C = 97° 17' 42''.
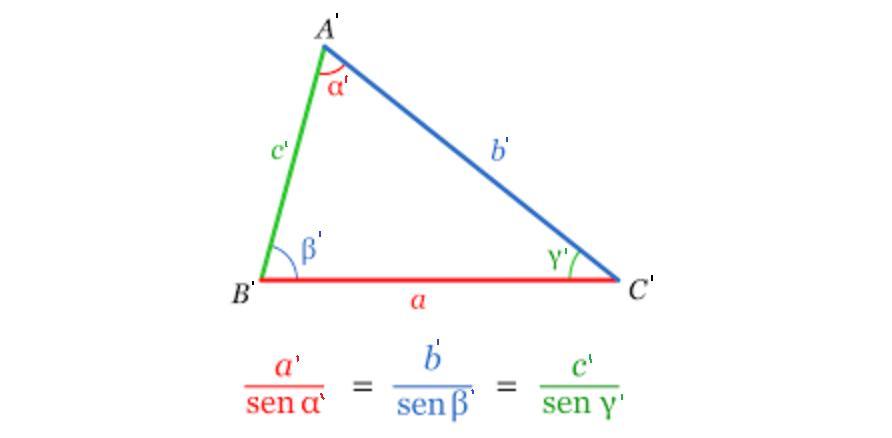
Now, from trigonometry, we know that the Law of Sine states that:
Using the equation that relates a' and c', we have:
\(\begin{gathered} \frac{a^{\prime}}{\sin\alpha^{\prime}}=\frac{c^{\prime}}{\sin\gamma^{\prime}}, \\ a^{\prime}=c^{\prime}*\frac{\sin\alpha^{\prime}}{\sin\gamma^{\prime}}. \end{gathered}\)Replacing the values from above, we get:
\(EA=a^{\prime}=440.68*\frac{\sin(97°17^{\prime}42^{\prime\prime}^)}{\sin(22°36^{\prime}9^{\prime\prime})}\)Side AE
From the picture, we see a triangle EDB. Using the data of the picture, we have:
• b' = ED = 470.43,
,• ∠E = 60° 06' 09'',
,• a' = EB = ?,
,• α' = ∠D = 180° - 87° 20' 24'' = 92° 39' 36'',
,• β' = ∠B = 180° - ∠D - ∠E = 180° - 92° 39' 36'' - 60° 06' 09'' = 27° 14' 15''.
Applying the law of sines, we have that:
\(\begin{gathered} \frac{a^{\prime}}{\sin(\alpha^{\prime})}=\frac{b^{\prime}}{\sin(\beta^{\prime})}, \\ EB=a^{\prime}=b^{\prime}*\frac{\sin(\alpha^{\prime})}{\sin(\beta^{\prime})}. \end{gathered}\)Replacing the values from above, we get:
\(undefined\)s
Answer
s
I'm having an issue with the middle part of the logarithmic equation

Answers
The obtained function is :
\(A=5500e^{0.07t}\)The question for the 3rd part is, how long will it be to have $14500 in the account.
Substitute A = 14500 and solve for the value of t :
\(\begin{gathered} 14500=5500e^{0.07t} \\ \Rightarrow\frac{14500}{5500}=e^{0.07t} \\ \Rightarrow\ln \frac{14500}{5500}=0.07t \\ \Rightarrow t=\frac{\ln \frac{14500}{5500}}{0.07} \\ \Rightarrow t=13.849 \end{gathered}\)Rounded to 2 decimal places, the value of t will be :
\(t=13.85\text{years}\)For the next question, the value of t when the amount is doubled :
\(\begin{gathered} 2(5500)=5500e^{0.07t} \\ 2=e^{0.07t} \\ \ln 2=0.07t \\ t=\frac{\ln 2}{0.07} \\ t=9.902 \end{gathered}\)The answer is 9.90 years
Select the correct answer from each drop-down menu.
Points A, B, and C form a triangle. Complete the statements to prove that the sum of the interior angles of ΔABC is 180°.
Statement Reason
Points A, B, and C form a triangle. given
Let be a line passing through B and parallel to . definition of parallel lines
∠3 ≅ ∠5 and ∠1 ≅ ∠4
m∠1 = m∠4 and m∠3 = m∠5
m∠4 + m∠2 + m∠5 = 180° angle addition and definition of a straight line
m∠1 + m∠2 + m∠3 = 180° substitution
Answers
Answer:
i hope this help
Step-by-step explanation:
Statement Reason
Points A, B, and C form a triangle. Given
Let be a line passing through B and parallel to . Definition of parallel lines
∠3 ≅ ∠5 and ∠1 ≅ ∠4 Definition of corresponding angles in parallel lines
m∠1 = m∠4 and m∠3 = m∠5 Substitution of corresponding angles
m∠4 + m∠2 + m∠5 = 180° Angle addition and definition of a straight line
m∠1 + m∠2 + m∠3 = 180° Substitution.
PLEASE HELP WITH THIS ONE QUESTION

Answers
Rachel has a bag containing 3 red marbles, 5 purple marbles, and 10 blue marbles.
What is the probability that she will pull a purple marble out of the bag? What is the
complement?
Answers
Answer:
5/18, 13/18
Step-by-step explanation:
The basic probability of anything is Specific Outcome / Total Outcomes
The specific outcome here is pulling a purple marble. We see there are 5 purple marbles therefore there are 5 ways to get them. The total outcomes are the total number of marbles which is 18. Therefore, the answer is 5/18
The complement of a probability is 1 minus the original probability, so, it would be 1 - 5/18 here getting us 13/18 as the answer.
-
1. Find all critical numbers for the function: f(x) = (9 - x2)3/5
A. {0}
B. {-3,3}
C. {3}
D. {-3,0,3}
Answers
Answer:
its easy
Step-by-step explanation: