6a-1÷7=4. . . . . . . . . . .. . .
Answers
Answer:
a=29/42
Step-by-step explanation:
6a-1÷7=4
first write the division as a fraction
6a-1/7=4
add 1/7 to each side
6a=4+1/7
which is equal to
6a=29/7
divide both sides by 6
a=29/42
Related Questions
Translate each equation. Do not solve.
The quotient of a number increased by 4 and -3 is 15
Answers
Answer:
a /4+-3=15?
Step-by-step explanation:
a. Find the derivative function f' for the function f.
b. Determine an equation of the line tangent to the graph of f at (a,f(a)) for the given value of a.
f(x) = 6/5x+3 a=-1
Answers
a.. F'(x) = 6/5 is the derivative function for the expression f(x) = (6/5)x + 3. b. y - (9/5) = (6/5)(x + 1) is the equation of the tangent line to the graph of f at (-1, f(-1)).
a. The power rule for derivatives can be used to determine the derivative function f'(x) for the function f(x) = (6/5)x + 3. The power rule states that the derivative of a function \(f(x) = ax^n\) is given by \(f'(x) = nax^{(n-1)\).
Applying the power rule to f(x), we have:
\(f'(x) = (6/5)(1)x^{(1-1) }= (6/5)x^0 = 6/5\)
Therefore, the derivative function f'(x) for f(x) = (6/5)x + 3 is f'(x) = 6/5.
b.We must ascertain the slope of the tangent line at that location in order to ascertain the equation of the line tangent to the graph of f at (a, f(a)) for a = -1.
We are aware that the derivative of the function at that location determines the slope of the tangent line. The slope of the tangent line is also 6/5 because we discovered in part (a) that f'(x) = 6/5.
The equation of the tangent line can be expressed using the point-slope form of a linear equation as follows:
y - f(a) = m(x - a)
Plugging in the values a = -1, f(a) = f(-1), and m = 6/5, we have:
y - f(-1) = (6/5)(x - (-1))
To find f(-1), substitute x = -1 into the original function f(x):
f(-1) = (6/5)(-1) + 3 = -6/5 + 3 = 9/5
Now we can rewrite the equation of the tangent line:
y - 9/5 = (6/5)(x + 1)
This equation is in point-slope form and represents the line tangent to the graph of f(x) = (6/5)x + 3 at the point (-1, 9/5).
Learn more about derivative here: https://brainly.com/question/32963989
#SPJ11
if f(x)= -x^2-3x+5, find f(-3)
Answers
Answer:
5
Step-by-step explanation:
-9-(-9)+5=5
Write the equation of a parabola whose directrix is x=4 and has a focus at (-6,-5).
Write the equation of a parabola whose directrix is y=2 and has a focus at (3,10).
Find the equation for the parabola that has its focus at (-3,2) and has directrix y=6.
Find the equation for the parabola that has its vertex at the origin and has directrix at x=-1/43.
Find an equation for the parabola that has its vertex at the origin and has its focus at the point (0,-6.4).
Answers
The equations of the parabolas are: (a) (x + 5)^2 = 8(y + 6) (b) (y - 6)^2 = 4(x - 0)
(c) (y - 0)^2 = 16(x + 1/43) (d) (y + 6.4)^2 = 4y
(a) To find the equation of a parabola with directrix x = 4 and focus at (-6, -5), we can use the formula: (x - h)^2 = 4p(y - k), where (h, k) is the vertex and p is the distance between the vertex and the focus. In this case, the vertex is (-6, -5), and p is the distance from (-6, -5) to the directrix x = 4, which is 10 units. Plugging in the values, we get (x + 6)^2 = 8(y + 5).
(b) For a parabola with directrix y = 2 and focus at (3, 10), we use the formula: (y - k)^2 = 4p(x - h). The vertex is (3, 10), and the distance between the vertex and the directrix y = 2 is 8 units. Plugging in the values, we get (y - 10)^2 = 32(x - 3).
(c) To find the equation for a parabola with focus at (-3, 2) and directrix y = 6, we can use the formula (y - k)^2 = 4p(x - h). The vertex is the midpoint between the focus and the directrix, which is (-3, 4). The distance between the vertex and the focus (or directrix) is the value of p, which is 2 units. Plugging in the values, we get (y - 4)^2 = 16(x + 1/43).
(d) For a parabola with vertex at the origin and focus at (0, -6.4), we can use the formula (x - h)^2 = 4p(y - k). The vertex is (0, 0), and the distance between the vertex and the focus (or directrix) is the value of p, which is 6.4 units. Plugging in the values, we get (y - 0)^2 = 4(6.4)y, which simplifies to y^2 = 4(6.4)y.
Learn more about Parabola here: brainly.com/question/11911877
#SPJ11
(A lot of points to whoever can help me out!!) I need help with this!!

Answers
The completed statements with regards to the compound interest of the amount in the account are;
If the account has a 5% interest rate and is compounded monthly, you have $101.655 million money after 2 years
If the account has a 5% interest rate compounded continuously, you would have $106.096 million money after 2 years
What is the compound interest on an amount?Compound interest is the interest calculated based on the initial amount and the accumulated interests accrued from the periods before the present.
The compound interest formula indicates that we get;
\(A = P\cdot (1 + \frac{r}{n}) ^{n\cdot t}\)
Where;
P = The principal amount invested = $92 million
r = The interest rate = 5% monthly
n = The number of times the interest is compounded per annum = 12
t = The number of years = 2 years
Therefore; \(A = 92\cdot (1 + \frac{0.05}{12}) ^{12\times 2}\approx 101.655\)
The amount in the account after 2 years is therefore about $101.655 million
The formula for the amount in the account if the principal is compounded continuously, we get;
A = \(P\cdot e^{(r\cdot t)}\)
Therefore, we get;
\(A = 96 \times e^{0.05 \times 2} \approx 106.096\)
The amount in the account after 2 years, compounded continuously therefore, is about $106.096 million
Learn more on compound interest here: https://brainly.com/question/21487182
#SPJ1
if the scale in the drawing is 1/4inch=3miles, what is the distance, in miles between Hawthorne an Doylestown?(help)

Answers
We will investigate how to use ratios to determine the actual distance between cities as per defined scale.
We are given a scale conversion ( ratio ) at which distances are scaled down:
\(\begin{gathered} \text{Scale : Actual} \\ \frac{3}{4}\text{ in : }3\text{ miles} \end{gathered}\)We will use the given scale ratio to determine the actual distance between two citites. The scale distance between Hawthorne and Doyelstown can be read.
\(\text{Scale distance = 1.75 in}\)Now utilize the scale conversion ratio to determine the actual distance:
\(\begin{gathered} \text{Scale : Actual } \\ \frac{3}{4}in\text{ : 3 miles} \\ \\ 1.75\text{ in: x} \\ ======= \\ \\ \frac{3}{4}\cdot x\text{ = 3}\cdot1.75 \\ \\ x\text{ = }\frac{3\cdot1.75\cdot4}{3} \\ \\ x\text{ = 7 miles} \end{gathered}\)Therefore, the distance between Hawthorne and Doylestown is:
\(7\text{ miles}\)
Below is the graph of y=4^x. Translate it to become the graph of y=4^x+3 -1.
Answers
The translation from y = \(4^x\) to y = \(4^x\) + 3 - 1 are:
- Translating vertically 3 units up.
- Translating vertically 1 unit down.
What is translation?It is the movement of the shape in the left, right, up, and down directions.
The translated shape will have the same shape and shape.
There is a positive value when translated to the right and up.
There is a negative value when translated to the left and down.
We have,
y = \(4^x\) and y = \(4^x\) + 3 - 1
Now,
y = \(4^x\)
Translating vertically 3 units up we get,
y = \(4^x\) + 3
Again,
Translating vertically 1 unit down we get,
y = \(4^x\) + 3 - 1
Thus,
The translation from y = \(4^x\) to y = \(4^x\) + 3 - 1 are:
- Translating vertically 3 units up.
- Translating vertically 1 unit down.
Learn more about translation here:
https://brainly.com/question/12463306
#SPJ1
in triangle ABC, AB = 6 cm, BC = 13cm and angle ACB = 23 degrees. Calculate angle BÁC, which is obtuse.

Answers
Answer:
\(\angle BAC=180^{\circ}-\frac{13\sin 23^{\circ}}{6}\)
Step-by-step explanation:
\(\frac{\sin(\angle BAC)}{13}=\frac{\sin 23^{\circ}}{6} \\ \\ \sin \angle BAC=\frac{13\sin 23^{\circ}}{6} \\ \\ \angle BAC=180^{\circ}-\frac{13\sin 23^{\circ}}{6}\)
A typical person begins to lose consciousness if subjected to accelerations greater than about 5 g(49.0 m/s^2) for more than a few seconds. Suppose a 3.00×10^4−kg manned spaceship's engine has an exhaust speed of 2.50×10^3 m/s. What maximum burn rate ∣ΔM/Δt∣ could the engine reach before the ship's acceleration exceeded 5 g and its human occupants began to lose consciousness?
Answers
The maximum burn rate ∣ΔM/Δt∣ that the engine could reach before the ship's acceleration exceeded 5 g and its human occupants began to lose consciousness is approximately 51.0 kg/s.
Acceleration is directly proportional to the force acting on an object. In simple terms, if the force on an object is greater, then it will undergo more acceleration. However, there are limitations to the acceleration that can be tolerated by the human body. At about 5 g (49.0 m/s2) for more than a few seconds, an average person starts to lose consciousness. Let's use this information to answer the given question.
Let the maximum burn rate |ΔM/Δt| that the engine could reach before the ship's acceleration exceeded 5 g be x.
Let the mass of the spaceship be m and the exhaust speed of the engine be v.
Using the formula for the thrust of a rocket,
T = (mv)e
After substituting the given values into the formula for thrust, we get:
T = (3.00 × 104)(2.50 × 103) = 7.50 × 107 N
Therefore, the acceleration produced by the engine, a is given by the formula below:
F = ma
Therefore,
a = F/m= 7.50 × 107/3.00 × 104= 2.50 × 103 m/s²
The maximum burn rate that the engine could reach before the ship's acceleration exceeded 5 g is equal to the acceleration that would be produced by a maximum burn rate. Therefore,
x = a/5g= 2.50 × 103/(5 × 9.8)≈ 51.0 kg/s
Therefore, the maximum burn rate ∣ΔM/Δt∣ that the engine could reach before the ship's acceleration exceeded 5 g and its human occupants began to lose consciousness is approximately 51.0 kg/s.
Learn more about maximum burn rate
https://brainly.com/question/29328145
#SPJ11
Which of the following differential equation(s) is/are linear? (Choose all that apply.) 1 2xy" - 5xy' + y = sin(3x) (v)² + xy =In(x) □y' + sin(y)=e3x (x²+1)y"-3y - 2x³y=-x-9 (+1)y'+xy=y"
Answers
To determine which differential equation(s) are linear, we need to examine the form of each equation. A linear differential equation is one that can be written in the form a(x)y" + b(x)y' + c(x)y = g(x), where a(x), b(x), c(x), and g(x) are functions of x.
The differential equation 2xy" - 5xy' + y = sin(3x) is linear. It can be written in the form a(x)y" + b(x)y' + c(x)y = g(x), where a(x) = 2x, b(x) = -5x, c(x) = 1, and g(x) = sin(3x).
The differential equation (v)² + xy = In(x) is not linear. It does not follow the form a(x)y" + b(x)y' + c(x)y = g(x) because it contains a term with (v)², where v represents the derivative of y with respect to x. This term does not have a linear coefficient.
The differential equation y' + sin(y) = e^(3x) is linear. It can be written in the form a(x)y' + b(x)y = g(x), where a(x) = 1, b(x) = sin(y), and g(x) = e^(3x).
The differential equation (x²+1)y" - 3y - 2x³y = -x - 9 is not linear. It does not follow the form a(x)y" + b(x)y' + c(x)y = g(x) because it contains a term with (x²+1)y", where the coefficient is a function of x.
The differential equation y' + xy = y" is linear. It can be written in the form a(x)y' + b(x)y = g(x), where a(x) = 1, b(x) = x, and g(x) = y".
Learn more about differential equation here
https://brainly.com/question/32524608
#SPJ11
What volume of water can the aquarium hold?
A. 111 cm3
B.1433 cm3
C. 23,100 cm3
D. 46,200 cm3

Answers
Answer:
46,200 cm³
Step-by-step explanation:
The volume of a rectangular prism: length * width * height
Multiply:
length * width * height50 * 28 * 3346,200The units are cm * cm * cm or cm³
\(\boxed{\text{The volume is 46,200 cm}^3}\)
-Chetan K
The volume that can be held by the aquarium is 46,200 cm³
What is volume?Volume can be regarded as scalar quantity expressing the amount of three-dimensional space enclosed by a closed surface.
Using the formula
Volume= (length * width * height)
=(50 * 28 * 33)
=46,200 cm³
Learn more about Volume at:
https://brainly.com/question/23963432
Mr. Bill leaves O'Fallon traveling at an average speed of 50 mph. Fifteen minutes later his wife leaves O'Fallon
traveling at 52 mph. How far did Mr. and Mrs. Bill travel when they met up with each other?
Answers
Mr. and Mrs. Bill traveled 12.5 miles when they met up with each other.
Let's start by converting the 15 minutes delay of Mr. Bill's departure into hours:
15 minutes = 15/60 = 0.25 hours
Next, we can use the formula:
distance = speed x time
to calculate the distance traveled by each person before they meet up.
For Mr. Bill, the distance he traveled before meeting his wife is:
distance = speed x time
distance = 50 mph x 0.25 hours
distance = 12.5 miles
For Mrs. Bill, we need to account for the 15 minutes head start Mr. Bill had. So, her time traveled will be slightly longer than Mr. Bill's:
time = distance / speed
time = (12.5 miles) / (52 mph)
time = 0.24 hours
Her distance traveled will be:
distance = speed x time
distance = 52 mph x 0.24 hours
distance = 12.48 miles
To find the total distance traveled when they met up, we add the distances traveled by each person:
total distance = distance traveled by Mr. Bill + distance traveled by Mrs. Bill
total distance = 12.5 miles + 12.48 miles
total distance = 24.98 miles
Rounding to the nearest tenth of a mile, we get that Mr. and Mrs. Bill traveled 12.5 miles when they met up with each other.
For more questions like Distance click the link below:
https://brainly.com/question/15172156
#SPJ11
(2x^2)^3(-x^4)
can somebody please help me on this
Answers
Answer:
\(({2x}^{2} )^{3} \times ( - {x}^{4} )\)
\( {2x}^{6} \times ( - {x}^{4} )\)
\( - {2x}^{6 + 4} \)
\( - {2x}^{10} \)
hope it helps you :)
Could you please help me with number 6 thank you sm !!

Answers
Answer:
A) a = 4, b = 3Step-by-step explanation:
#6Given equation:
4/(x - 3) + 2/(x - 2) = 2Multiply all terms by (x - 3)(x - 2):
4(x - 2) + 2(x - 3) = 2(x - 3)(x - 2)2(x - 2) + (x - 3) = (x - 3)(x - 2)2x - 4 + x - 3 = x² - 5x + 6x² - 5x - 3x + 6 + 7 = 0x² - 8x + 13 = 0x = (8 ± √(8² - 4*13))/2 = (8 ± √12)/2 = (8 ± 2√3)/2 = 4 ± √3Compare this to the given form to get:
a = 4, b = 3Correct choice is A
On solving
x=4±√3
So
a=4 and b=3
Please help me ASAP!!! Answer both questions for example: 1= C and 2= A
Answers
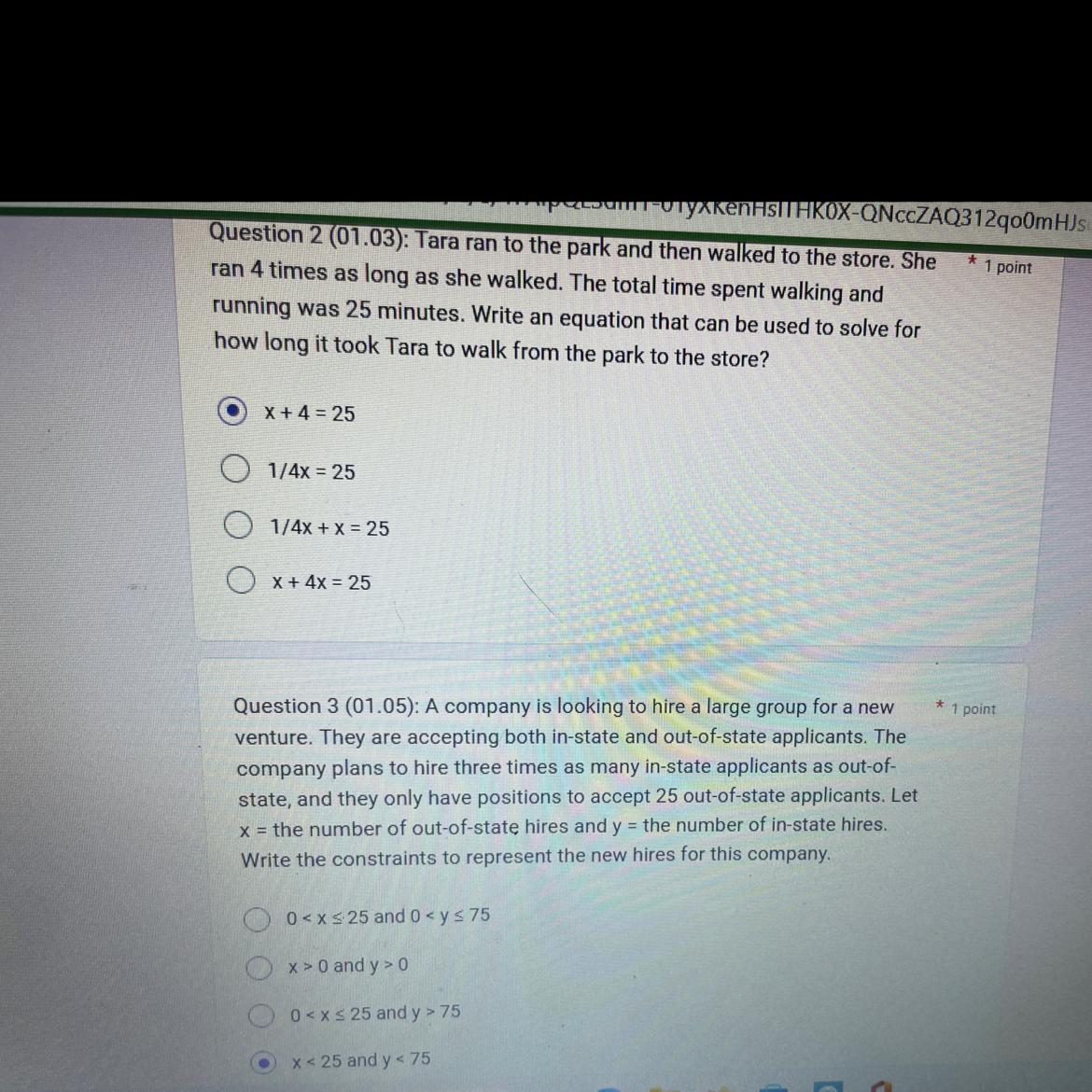
2. The equation is given as follows: x + 4x = 25.
3. The constrains are given as follows: 0 ≤ x ≤ 25, 0 ≤ y ≤ 75.
What is the equation in item 2?The time spent running is given by:
Running = 4x.
The time spent walking is one-fourth of the time spent walking, hence it is given by:
Walking = 4x/4 = x.
The total time is the sum of the times spent running and walking, hence the expression is presented as follows:
x + 4x = 25.
What are the constraints in item 3?The variables are given as follows:
x: number of out-of-state hires.y: number of in-state hires.You can accept at most 25 out-of-state hires, hence:
0 ≤ x ≤ 25
(as the number cannot be negative).
The company plans to have three times as many in-state hires, hence:
0 ≤ y ≤ 75.
As:
3 x 0 = 0.3 x 25 = 75.More can be learned about equations and constraints at https://brainly.com/question/18435162
#SPJ1
Do the ratios 10:12 and 1:21 form a proportion?
Answers
No, the ratios 10:12 and 1:21 are not form a proportion.
What is Proportional?A relationship that is always in the same ratio and quantity which vary directly with each other is called the proportional.
Given that;
The ratios are,
⇒ 10 : 12 and 1 : 21
We know that;
Two ratio are form a proportional when both are in same quantity or in a a same ratio.
Here, The ratios are,
⇒ 10 : 12 and 1 : 21
Clearly, We get;
10 / 12 = 5 / 6
1 / 21 = 1 21
Thus,
1 / 21 ≠ 5 /6
1 : 21 ≠ 10 : 12
Therefore, The ratios 10:12 and 1:21 are not form a proportion.
Learn more about the proportion visit:
https://brainly.com/question/870035
#SPJ9
State the additional congruency statement needed to prove ABC FGH for the given theorem

Answers
ANSWERS
A. AB ≅ FG
B. ∡C≅ ∡H
EXPLANATION
A. To use SAS theorem, we have to know if one more side is congruent to the corresponding side of the other triangle. SAS is side-angle-side. The angle must be included between the two sides. Therefore the missing side is AB congruent to FG:
B. To use ASA Theorem we have to know one more angle. Since ASA is angle-side-angle, the side must be between two angles. Therefore, the missing angle is angle C congruent to angle H:


Your favorite cookies use 2 1/2 cups flour per batches. You used 7 cups. How many batches did you make?
here are the anwser choices:
a. 3 1/4
b. 3 4/5
c. 2 4/5
d. 2 1/4
please help me
Answers
Answer:
3 and a fourth amount of bathces
Mary said, "Four times my age reduced by thirty is six. How old am I?
Answers
Answer:
9
Step-by-step explanation:
I said so
Mr. Beber feeds his dog 1/5 of a cup of dog food each day. How long will 9 cups of dog food last?
Answers
Answer:
45 days
Step-by-step explanation:
Step 1: Determine how long it will last
(9 cups) * (5 days / cup)
45 days
Answer: 45 days
Brady has $20,000 in student loans with 3.3% interest that he plans to pay off in 5 years. Find the total cost of repayment.
Answers
The total cost of repayment over 5 years is $23,300.
What is the total cost of repayment?A loan repayment refers to the act of paying back money previously borrowed from a lender.
To get total cost of repayment, we must principal amount, the interest rate and the duration of the loan.
The formula to get total cost of repayment is given by \(Total Cost of Repayment = Principal + Interest\)
Interest = Principal * Interest Rate * Time
Given:
Principal amount is $20,000
Interest rate is 3.3%
Duration is 5 years.
Interest = $20,000 * 0.033 * 5
Interest = $3,300
Total Cost of Repayment = Principal + Interest
= $20,000 + $3,300
= $23,300.
Read more about repayment
brainly.com/question/25696681
#SPJ1
Find the rate of change in the graph

Answers
Answer:
4/3
hope this helped :)
Solve the given differential equation by undetermined coefficients
1/4 y'' + y' + y = x2 − 3x
Answers
y ( x) = \(C_{1} e^{-2x} + C_{2} e^{-2x} + x^{2} - 5 x + \frac{9}{2}\) is the result of solving the subsequent differential equation with unknown coefficients.
What do you mean by differential equation ?One or more functions and [some of] their derivatives are connected by a differential equation. The [first] derivative of the function with respect to the variable is illustrated in the following example. Differentials are a term used to describe the and elements.
given
1/4 y'' + y' + y = x2 − 3x
The auxilary equation is
1/4 \(m^{2}\) + m + 1 = 0
\(m^{2}\) + m + 1 = 0
\(( m- 2)^{2}\) = 0
m = -2 , -2
= A =1 , 2A+ B = -3 , 1/2A + B = 0
A = 1 , B = - 5 , C = 9/ 2
Then the general solution is
y = yc + yp
y ( x) = \(C_{1} e^{-2x} + C_{2} e^{-2x} + x^{2} - 5 x + \frac{9}{2}\) is the result of solving the subsequent differential equation with unknown coefficients.
To know more about differential equation visit :-
https://brainly.com/question/14620493
#SPJ4
What are the 6 trigonometric identities?
Answers
The six trigonometric identities are:
cosecant(x) = 1/sin(x) secant(x) = 1/cos(x) csc(x) = 1/sin(x) sec(x) = 1/cos(x) tan(x) = sin(x)/cos(x) cot(x) = cos(x)/sin(x)Trigonometry is the branch of mathematics that deals with the relationships between the angles and sides of triangles. In trigonometry, there are six basic functions, sine, cosine, tangent, cosecant, secant, and cotangent, each of which is represented by a specific letter. These functions are related to each other through a set of identities known as the trigonometric identities.
The six trigonometric identities listed above, are the most commonly used identities, and provide the relationships between the six trigonometric functions and each other. They are useful for solving trigonometric equations, simplifying trigonometric expressions, and solving problems in geometry, physics, engineering and other sciences.
The Pythagorean identity states that the sum of the squares of the sine and cosine of an angle is equal to 1, which is a fundamental relationship between the two functions. The reciprocal identities state that the reciprocal of the sine and cosine of an angle is equal to the cosecant and secant of that angle respectively.
The quotient identities state that the tangent of an angle is equal to the sine of that angle divided by the cosine of that angle, and the cotangent of an angle is equal to the cosine of that angle divided by the sine of that angle.
It's important to note that these identities are valid for all values of the angle, and are true in any angle measurement system (degrees or radians).
To know more about trigonometric identities on the link below:
https://brainly.com/question/24377281#
#SPJ11
Find an equation for the hyperbola with foci (0,±5) and with asymptotes y=± 3/4 x.
Answers
The equation for the hyperbola with foci (0,±5) and asymptotes y=± 3/4 x is:
y^2 / 25 - x^2 / a^2 = 1
where a is the distance from the center to a vertex and is related to the slope of the asymptotes by a = 5 / (3/4) = 20/3.
Thus, the equation for the hyperbola is:
y^2 / 25 - x^2 / (400/9) = 1
or
9y^2 - 400x^2 = 900
The center of the hyperbola is at the origin, since the foci have y-coordinates of ±5 and the asymptotes have y-intercepts of 0.
To graph the hyperbola, we can plot the foci at (0,±5) and draw the asymptotes y=± 3/4 x. Then, we can sketch the branches of the hyperbola by drawing a rectangle with sides of length 2a and centered at the origin. The vertices of the hyperbola will lie on the corners of this rectangle. Finally, we can sketch the hyperbola by drawing the two branches that pass through the vertices and are tangent to the asymptotes.
Know more about equation for the hyperbola here:
https://brainly.com/question/30995659
#SPJ11
6x + 5y = 5
9x - 4y = 19
Solve this concurrent equation.
Answers
6x=55y
9x=188y
sure it is concurent equation
Answer:
\(x = \frac{5}{3} , \ \ y = -1\)
Step-by-step explanation:
6x + 5y = 5 -----(1)
9x - 4y = 19 -----(2)
Multiply (1) by 9 : 54x + 45y = 45 ------(3)
Multiply (2) by 6 : 54x - 24y = 114 -------(4)
(3) - (4) ==> 69y = -69
y = -1
Substitute y = -1 in (1)
6x + 5(-1) = 5
6x - 5 = 5
6x = 5 + 5
6x = 10
\(x =\frac{10}{6} = \frac{5}{3}\)
5a) Determine the measure of each unknown angle

Answers
Answer:
Step-by-step explanation:
25, i think
Seven times a number is 12 less than thirteen times the same number. Find the number.
Answers
Answer:
number is 2
Step-by-step explanation:
let the number be n then 7 times the number is 7n and 12 less than 13 times the number is 13n - 12
equating the 2 expressions
7n = 13n - 12 ( subtract 13n from both sides )
- 6n = - 12 ( divide both sides by - 6 )
n = 2
that is the number n is 2
The answer is:
the number is 2
Work/explanation:
I am going to start by letting b be the number.
Seven times b is 7b.
13 times the same number means 13 times b: 13b
12 less than 13b: 13b - 12
Thus, the equation is 7b = 13b - 12
Now to solve!
Add 12 on each side
7b + 12 = 13b
Subtract 7b on each side
12 = 13b - 7b
12 = 6b
Divide each side by 12
2 = b
Hence, 2 is the number.Pls help I give brainliest

Answers
Answer:
B
Step-by-step explanation:
it's (m+n-1) √p
hope this helps
5elect the correct answer
Celeste can spend no more than $30 to buy quinoa and rice. She wll pay $5 per pound for quirnoa and $2 per pound for rice. Which graph best
represents the nunber of pounds of quinoa and the rurmber of pounds of rice Celeste can buy

Answers
Answer:
A
Step-by-step explanation: