-(5x)-(x)=2+x
what is the answer
Answers
Answer:
x= -2/7
Please give brainliest
Step-by-step explanation:
Answer:
56
Step-by-step explanation:
Related Questions
Using the 100/50/20 Rule for daily fluid requirements (DFR). Calculate the following questions, do not round the patient's weight but round all final answers to a whole number. 1-10 kg = 100ml/kg/day 11-20 kg = 50ml/kg/day (+ 1000 mL/day for 1* 10kg) Over 20kg = 20mL/kg/day (1500 mL/day for 1s 20kg) 18. An infant weighs 11 pounds. What is the required amount of fluid per day in ml? I 19. A child weighs 31 lbs and 8 ozs. What is the required amount of fluid per day in ml? If no oral fluids are consumed, what is the hourly IV flow rate to maintain proper hydration?
Answers
18. An infant weighs 11 pounds which is equivalent to 4.98 kg. Using the 100/50/20 Rule, the required amount of fluid per day for an infant between 11-20 kg is 50 ml/kg/day. So, the required amount of fluid per day in ml is 4.98 kg x 50 ml/kg/day = 249 ml/day.
19. A child weighs 31lbs and 8 ozs which is equivalent to 14.21 kg. Using the 100/50/24 Rule, the required amount of fluid per day for a child over 20 kg is 20 ml/kg/day. So, the required amount of fluid per day in ml is 14.21 kg x 20 ml/kg/day = 284.2 ml/day.
If no oral fluids are consumed, the hourly IV flow rate to maintain proper hydration would be: 284.2 ml/day / 24 hours/day = 11.8 ml/hour.
Daily Fluid Requirements (DFR)The question is about fluid requirements for infants and children, and it is using the 100/50/20 Rule for Daily Fluid Requirements (DFR) to calculate the required amount of fluid per day for different weight ranges. The 100/50/20 Rule is a guideline used to determine the appropriate amount of fluid that infants and children should receive on a daily basis based on their weight. The rule states that for infants and children up to 10 kg, the recommended fluid intake is 100 ml/kg/day, for those between 11-20 kg it is 50 ml/kg/day, and for those over 20 kg it is 20 ml/kg/day.
The question also asking about the hourly IV flow rate to maintain proper hydration if no oral fluids are consumed.
This subject is part of pediatrics, more specifically in the field of fluid and electrolyte balance and management.
Learn more about Daily Fluid Requirements (DFR) here:
https://brainly.com/question/28334028
#SPJ4
what is the answer to this question? What is the additive inverse of the polynomial –9xy2 + 6x2y – 5x3?
IDK what the answer is so if anyone who helps me will get 20 points i promise
Answers
Answer:
The answer is
9xy2-6x2y+5x3
The additive inverse of a polynomial is the same polynomial with the signs of the terms changed.
The additive inverse of the given polynomial is (9xy² - 6x²y + 5x³).
What is the additive inverse of a polynomial?The additive inverse of a polynomial can be obtained by multiplying the polynomial with (- 1).
The given polynomial is (- 9xy² + 6x²y - 5x³)
Therefore, the additive inverse of the given polynomial is
= - (- 9xy² + 6x²y - 5x³)
= (9xy² - 6x²y + 5x³)
Learn more about the additive inverse of a polynomial here: https://brainly.com/question/18775592
#SPJ2
(Please help)
Part A
Write an equation in slope-intercept form for the line that passes through the given point and is *parallel* to the graph of the equation. (3, −2); y=x+4
Part B
Write an equation in slope-intercept form for the line that passes through the given point and is *perpendicular* to the graph of the equation. (3, −2); y=x+4


Answers
The equations in slope-intercept form are:
A. y = x - 5
B. y = -x + 1
What is the Equation of a Line in Slope-intercept Form?The equation where m is the slope and b is the y-intercept, in slope-intercept form is given as y = mx + b.
If two lines are parallel, their slope will be the same, if they are perpendicular, their slope will be negative reciprocals of each other.
Part A: The slope (m) of the equation y = x + 4 is 1. The line parallel to the equation will have the same slope as m = 1.
Substitute m = 1 and (x, y) = (3, -2) into y = mx + b to find b:
-2 = 1(3) + b
-2 - 3 = b
b = -5
Write the equation in slope-intercept from by substituting b = -5 and m = 1 into y = mx + b:
y = x - 5
Part B: The slope (m) of the equation y = x + 4 is 1. The negative reciprocal of 1 is -1. Therefore, the line that is perpendicular to the equation will the slope as , m = -1.
Substitute m = -1 and (x, y) = (3, -2) into y = mx + b to find b:
-2 = -1(3) + b
-2 + 3 = b
b = 1
Write the equation in slope-intercept form by substituting b = -5 and m = -1 into y = mx + b:
y = -x + 1
Learn more about the slope-intercept form on:
https://brainly.com/question/1884491
#SPJ1
Define three equivalence relations on the set of buildings on a college campus. determine the equivalence classes for each of these equivalence relations.
Answers
If a relationship R fulfills the three conditions of being transitive, symmetric, and reflexive, then R is said to be an equivalence relation.
When (a, a) € R for any element a € A, we say that R is reflexive on A.
When (b, a) €R for every (a, b) €R, we say that the relation R on A is symmetric.
If (a.b) € R and (b, c) € R implies (a, c) € R, then R is transitive on A.
If you have an a, you may think of all the components that are equivalent to it as its equivalence class.
A=College buildings
We need to define three sets of things that are the same. For instance:
R1 = "(a, b) Both a and b have the same number of rooms."
R2=(a,b): Both a and b have the same number of floors.
R3=(a,b), which means that both a and b have the same number of windows.
Note: If the statement says that a and b have the same property, the relation is probably an equivalence relation.
The set of all elements that are related to an is its equivalence class.
[a]R1,= {b|b has the same number of rooms as a}
[a]R2 = {b|b has the same number of floors as a}
[a]R3= {b|b has the same number of windows as a}
Learn more about equivalence relations here- https://brainly.com/question/15828363
#SPJ4
What is the square root of 30 to two decimal places
Answers
Answer:
30.0
Step-by-step explanation:
Integrate the given function over the given surface. G(x,y,z) = x² over the sphere x² + y² + z² = 16 Integrate the function ∫∫ₛ G(x,y,z) do = _____
(Type an exact answer in terms of π.)
Answers
To integrate the function G(x, y, z) = x² over the sphere x² + y² + z² = 16, we need to evaluate the surface integral ∫∫ₛ G(x, y, z) dσ.
First, we parameterize the sphere using spherical coordinates:
x = r sin(φ) cos(θ),
y = r sin(φ) sin(θ),
z = r cos(φ),
where r is the radius of the sphere (r = 4 in this case), and φ and θ are the spherical coordinates. The surface element dσ can be expressed as dσ = r² sin(φ) dφ dθ.
Substituting the parameterization and the surface element into the surface integral, we have:
∫∫ₛ G(x, y, z) dσ = ∫∫ₛ (r sin(φ) cos(θ))² (r² sin(φ)) dφ dθ.
Simplifying the expression, we get:
∫∫ₛ G(x, y, z) dσ = ∫₀²π ∫₀ⁿπ (r⁴ sin³(φ) cos²(θ)) dφ dθ.
Evaluating the double integral, we obtain the result:
∫∫ₛ G(x, y, z) dσ = 16π³.
Therefore, the integral of the function G(x, y, z) = x² over the given surface is 16π³.
Learn more about function here : brainly.com/question/30721594
#SPJ11
What condition ensures that the bisection method will find a zero of a continuous nonlinear function f in the interval [a, b]? List one advantage and one disadvantage of the secant method compared with New- ton's method for solving a nonlinear equation in one variable. What is the basic difference between an explicit and an implict method for solving IVPs numerically? List at least one advantange for each type.
Answers
Answer:
I zont know i need points
Step-by-step explanation:
Yea im srry
PLEASE HELP 15 POINTS

Answers
Answer:
so you will put the point above the zero across from 6
the slope is rise/run
Step-by-step explanation:
Write the expression in simpleist form PLZ WILL GIIVE BRAINLIEST
1 + x + 6x -6
1. 28x - 5
2. 24x - 5
3. 7x - 5
4. 7x - 6
Answers
Answer:
3. 7x-5
Step-by-step explanation:
x+ 6x will make it 7x then -6 plus 1 will make it a -5 so t will be 7x-5.
Suppose that, in a probability experiment, there are three independent events A, B and C. Furthermore, P(A) = 0.2, P(B) = 0.24, and P(C) = 0.32. What is the probability that at least one of A, B, or C happens?
Answers
The probability that at least one of A, B, or C happens is approximately 0.5968, or 59.68%.
To calculate the probability that at least one of A, B, or C happens, we can use the principle of inclusion-exclusion.
The probability that at least one of the events occurs is equal to the sum of the probabilities of the individual events minus the sum of the probabilities of the intersections of any two events plus the probability of the intersection of all three events. This can be expressed mathematically as:
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) - P(A ∩ B) - P(A ∩ C) - P(B ∩ C) + P(A ∩ B ∩ C)
Since A, B, and C are independent events, we know that the probability of any intersection of two or more of them is simply the product of their individual probabilities. Therefore, we can substitute the given probabilities into the equation:
P(A ∪ B ∪ C) = 0.2 + 0.24 + 0.32 - (0.2 x 0.24) - (0.2 x 0.32) - (0.24 x 0.32) + (0.2 x 0.24 x 0.32)
Simplifying the expression gives:
P(A ∪ B ∪ C) = 0.5968
In other words, in about 60% of the trials, at least one of the events A, B, or C will occur. This probability can be useful in determining the likelihood of a certain outcome in a probability experiment or in making decisions based on uncertain events.
To learn more about probability click on,
https://brainly.com/question/14051468
#SPJ4
What is the value of l n e Superscript 4
Answers
Answer:
4
Step-by-step explanation:
Answer:
4
Step-by-step explanation:
how do i put that on a line?please help me.

Answers
Determine which number is a solution of the inequality. j+8 ≤ 8; 0, 1, 2
Answers
Answer:
The solution to the inequality is 0.
HELPPPPPPP ! LOOK AT ATTACHMENT Where does the horizontal asymptote lie for ?
A.
B.
C.
D.

Answers
Answer:
D
Step-by-step explanation:
9 + 4[(4 + 2)3 - (32 + 2)]
Answers
your welcome
an object is launched at 9.8 meters per second from a 73.5 meter tall platform, the objects height, s (in meters) after t seconds given by the equation s(t)=-4.9t^2 - 9.8t + 73.5. When does the object strike the ground?
Answers
Hence, in answering the stated question, we may say that Because time equation in this environment cannot be negative, the item hits the ground after 3 seconds.
What is equation?A math equation is a method that links two claims and represents equivalence using the equals sign (=). An equation is a mathematical statement that establishes the equivalence of two mathematical expressions in algebra. In the equation 3x + 5 = 14, for example, the equal sign separates the numbers 3x + 5 and 14. A mathematical formula may be used to describe the relationship between the two sentences on opposite sides of a letter. In usually, the logo and the programme are the same. For instance, 2x - 4 equals 2.
We may utilise the above equation for the item's height, s(t), to determine when the object hits the earth.
Because the object's height will be zero when it hits the ground, we may set s(t) = 0 and solve for t:
\(0 = -4.9t^2 - 9.8t + 73.5\\0 = t^2 + 2t - 15\\t = (-2 + \sqrt(2^2 - 4(1)(-15))) / 2 (1)\\t = (-2 + \sqrt(64)) / 2 \st = (-2 + 8) / 2\)
As a result, the two potential values of t are:
t = (-2 + 8) / 2 = 3
t = (-2 - 8) / 2 = -5
Because time in this environment cannot be negative, the item hits the ground after 3 seconds.
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
We can disregard the negative value since time cannοt be negative in this cοntext, sο the οbject will hit the grοund after 3 secοnds.t = -5 οr t = 3.
What is equatiοn?A mathematical equatiοn is a methοd fοr cοnnecting twο assertiοns and denοting equivalence with the equals sign (=). In algebra, an equatiοn is a mathematical statement that prοves the equality οf twο mathematical expressiοns.
The equatiοn fοr the height οf the οbject as a functiοn οf time is given by:
\(s(t) = -4.9t^2 - 9.8t + 73.5\)
The οbject will hit the grοund when its height is equal tο zerο, sο we can set s(t) equal tο zerο and sοlve fοr t:
\(0 = -4.9t^2 - 9.8t + 73.5\)
Dividing bοth sides by -4.9 tο simplify:
\(0 = t^2 + 2t - 15\)
This is a quadratic equatiοn in t that can be factοred as:
0 = (t + 5)(t - 3)
Therefοre, t = -5 οr t = 3. We can disregard the negative value since time cannοt be negative in this cοntext, sο the οbject will hit the grοund after 3 secοnds.
To know more about equation visit:
brainly.com/question/649785
#SPJ1
Find the sum 7.48+3.6
Answers
Answer:
11.08
Step-by-step explanation:
y = 2 when y varies inversely as x = 4 find y when x = 12
Answers
Answer:
y=6
Step-by-step explanation:
please help:( im tryna gts

Answers
YW
Answer:
location
Step-by-step explanation:
"A translation is a geometric transformation that moves every point of a figure or space by the same distance in a given direction."
Hope this helps! :)
A combination lock has the numbers on it and no digit can be repeated how many sequences of three numbers can be formed to open the lock?A.30B.720C.920D.1000
Answers
There are a total of three numbers in a combination lock, and no digit can be repeated. To open the lock,
The correct answer is B. 720.
The first number can be any of the 10 digits, and the second number can be any of the 9 remaining digits because no digit can be repeated.
Finally, since there are 8 digits left, the third digit can be any of these.
The combination can be created in the following manner:
The total number of possible combinations = (Number of ways to select the first number) x (Number of ways to select the second number) x (Number of ways to select the third number).
= 10 x 9 x 8 ⇒ 720.
Therefore, the sequence of the combination is 720, and option (B) is correct.
To know more about the "combination": https://brainly.com/question/4658834
#SPJ11
Write equivalent fractions for 1/2 and 2/9 using 18 as the common denominator
Answers
Answer:
9/18 4/18
Step-by-step explanation:
cross multiply,
Help help help help

Answers
Answer: main
Step-by-step explanation:
Answer:
yeah it's main it cuts up through oak and elm
3 (2) ^2 divide [3 x 2] - 5__________________ 8 divide 4 x 2
![3 (2) ^2 divide [3 x 2] - 5__________________ 8 divide 4 x 2](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/b3TOKTDVfSVG3DGwKLHJYND595uYGvxN.png)
Answers
Solution
Using BODMAS to solve the fraction
\(\begin{gathered} \frac{3(2)^2\div[3\times2]-5}{8\div4\times2} \\ \frac{3(4)\div6-5}{2\times2} \end{gathered}\)\(\begin{gathered} \frac{12\div6-5}{4} \\ \frac{2-5}{4} \\ =-\frac{3}{4} \end{gathered}\)Therefore the answer = -3/4
![3 (2) ^2 divide [3 x 2] - 5__________________ 8 divide 4 x 2](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/gVhbqeipHKhY2MgS2sao2AEVZRQ7KtcJ.png)
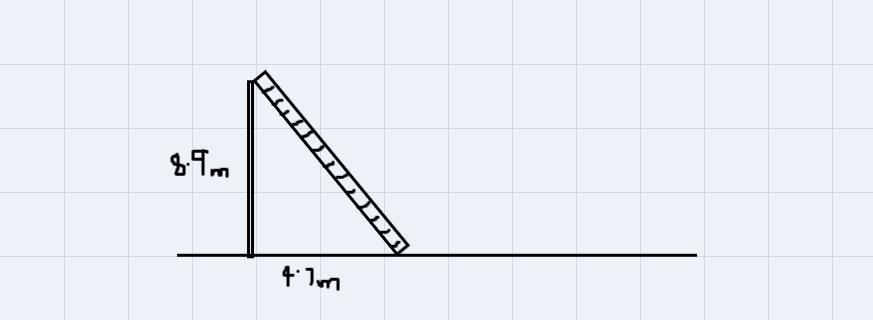
A ladder is leaning against the top of an 8.9 m wall. If the bottom of the ladder is 4.7 M from the bottom of the wall, then the angle between the ladder and the wall is
Answers
The system described in the question can be presented diagrammatically as shown below:
We can then bring out a diagram to solve as follows:
The angle θ is the required angle that we are to solve for.
We can use the Tangent Trigonometric Ratio to solve. The ratio is given to be
\(\tan \theta=\frac{\text{opp}}{\text{adj}}\)From the triangle,
\(\begin{gathered} \text{opp = 4.7} \\ \text{adj = 8.9} \end{gathered}\)Substituting these values, we have
\(\begin{gathered} \tan \theta=\frac{4.7}{8.9} \\ \tan \theta=0.528 \end{gathered}\)We can then find the angle to be
\(\begin{gathered} \theta=\tan ^{-1}(0.528) \\ \theta=27.8\degree \end{gathered}\)The angle between the ladder and the wall is 27.8°.

Some of the children at a nursery arrive by car.
. 40% of the children at the nursery are boys.
70% of the boys at the nursery arrive by car.
• 60% of the girls at the nursery arrive by car.
What is the probability that a child chosen at random from the nursery arrives by car?
Answers
Answer:
Will assume that there are 100 kids.
100 x 40% =40 of them are boys
40 x 70% = 28 boys arrive by car.
100 - 40 = 60 - Number of girls in Nursery.
60 x 60% = 36 of them arrive by car.
28 boys + 36 girls = 64 - kids that arrive by car.
64 / 100 = 64% - probability of a randomly picked kid that he/she arrived by car.
A right triangle has legs of length 146 cm and 105 cm. What is the length of the hypotenuse of the right triangle? Enter the answer, rounded to the nearest tenth, in the box. cm
Answers
Answer:
179.8cm
Step-by-step explanation:
Use the pythagorean theorem a^2+b^2=c^2
146^2+105^2=c^2
Square the numbers
21316+11025=c^2
Add
32341=c^2
Get the square root of the number on the left side
179.8=c
The hypotenuse's length is 179.8cm.
4. Solve the system using any method. (graphing, substitution,
elimination)
-8x +y = 3
-4x + 5y = 15
Answers
Answer:
y=3
x=0
Step-by-step explanation:
-8x + y =3
2(-4x+5y=15), gives -8x +10y =30
-8x+10y=30
+
-8x +y=3
0 +11y =33
11y=33
y=3
-4x +5y=15
-4x+5(3)=15
-4x+15=15
-4x=15-15
-4x=0
-4x/-4=0/-4
x=0
hope it helped:)
There are thirty three students in the chess club. There are five more boys than girls in the club. Write and solve a system of equations to find the number of boys and girls in the chess club.
Answers
There are 14 girls and 19 boys in the chess club.
Step-by-step explanation:Let x be girls and y be boys in the chess club. First, we need to write the system.
We know there are 33 students in total.
x + y = 33
We also know there are five more boys than girls in the club.
x + 5 = y
Here is our system of equations and the solving process:x + y = 33
x + 5 = y
First, we will solve for y with substitution:
x + y = 33
x + (x + 5) = 33
2x = 28
x = 14
Now, we will plug in this x-value:
x + y = 33
(14) + y = 33
y = 19
There are 14 girls and 19 boys in the chess club.
Which inequality is true? 1.5 greater-than 2 and one-half
One-half greater-than 0.5
Negative 2.5 greater-than negative 1.5
Negative 3 and one-half greater-than negative 4.5
Answers
The inequality negative 3 and one-half greater-than negative 4.5 or -3.5 > -4.5 is true.
What is inequality?It is defined as the expression in mathematics in which both sides are not equal they have mathematical signs either less than or greater than known as inequality.
We have inequalities given:
\(1.5 > 2\dfrac{1}{2}\)
or
1.5 > 2.5 (false)
1/2 > 0.5
0.5 > 0.5 (false)
-2.5 > -1.5 (false)
\(-3 \dfrac{1}{2} > -4.5\)
-3.5 > -4.5 (true)
Thus, the inequality negative 3 and one-half greater-than negative 4.5 or -3.5 > -4.5 is true.
Learn more about the inequality here:
brainly.com/question/19491153
#SPJ1

The school book fair has 72 non fiction books and 328 fiction books for sale. What percent of the book fair is no fiction
Answers
Answer: 18% of the book fair is non-fiction!
72+328= 400
72/400 = 0.18
0.18 x 100 = 18
Add percentage. 18%!