5.2.PS-14
Find 3 ratios that are equivalent to the given ratio.
10:16
Answers
Step-by-step explanation:
three ratios equivalent to 10:16
5:8, 20:32, 100:160
Related Questions
two point charges are placed on the x-axis as follows: charge q1 = 3.99 nc is located at x= 0.205 m , and charge q2 = 5.01 nc is at x= -0.302 m .
Answers
Two point charges, q1 = 3.99 nC located at x = 0.205 m and q2 = 5.01 nC at x = -0.302 m, are placed on the x-axis. The electric field and direction at a given point can be calculated using the principle of superposition.
The electric field at a point due to a point charge is given by Coulomb's law, E = kq/r^2, where E is the electric field, k is Coulomb's constant (8.99 x 10^9 Nm^2/C^2), q is the charge, and r is the distance between the point charge and the point where the electric field is being measured. To calculate the net electric field at a point due to multiple charges, we use the principle of superposition, which states that the total electric field at a point is the vector sum of the electric fields due to each individual charge.
In this case, we have two charges, q1 = 3.99 nC and q2 = 5.01 nC. The electric field at a point P on the x-axis, due to q1, can be calculated as E1 = kq1/r1^2, where r1 is the distance between q1 and point P. Similarly, the electric field at point P due to q2 can be calculated as E2 = kq2/r2^2, where r2 is the distance between q2 and point P. To find the net electric field at point P, we add the electric fields vectorially, E_net = E1 + E2.
To learn more about superposition click here: brainly.com/question/12493909
#SPJ11
4x -16 2x+16 linear pairs of angles

Answers
Answer:
\(\huge\boxed{\sf x = 30}\)
Step-by-step explanation:
Statement:Angles on a straight line add up to 180 degrees.
Solution:According to the statement,
4x - 16 + 2x + 16 = 180
Combine like terms4x + 2x - 16 + 16 = 180
6x = 180
Divide both sides by 6x = 180/6
x = 30\(\rule[225]{225}{2}\)
HELP ME ASAPPPPP!!!!

Answers
Thus, the explicit formula for the simple interest sequence A(n) = P + (n-1)(i.P) is: A(n) = P * (1 + i * (n-1)).
What is simple interest?Simple interest is a method of calculating interest on a loan or investment where interest is charged only on the initial principal amount. In simple interest, the interest rate is applied to the original principal amount, and the interest earned remains the same throughout the entire term of the loan or investment.
by the question.
The formula for a simple interest sequence A(n) = P + (n-1) (i.P) represents the value of an investment that earns simple interest over n periods, where:
A(n) is the value of the investment after n periods.
P is the principal or initial investment
i is the interest rate per period as a decimal fraction (e.g. 0.05 for 5%)
n is the number of periods
To derive the explicit formula for A(n), we can use the formula for simple interest:
I = P * i * n
where I am the total interest earned over n periods. We can then express A(n) as:
A(n) = P + I
Substituting the expression for I, we get:
A(n) = P + P * i * (n-1)
Simplifying, we can factor out P to get:
A(n) = P * (1 + i * (n-1))
To learn more about amount:
https://brainly.com/question/13024617
#SPJ1
Use Laplace transform to solve the following partial differential equation with prescribed boundary and initial data: Uz(x, t) + 2xut(x, t) = 2x, u(x,0) = 1, u(0,t) = 1, where x ER and t > 0. Show the details of your work.
Answers
The given partial differential equation is given by; Uz(x, t) + 2xut(x, t) = 2x
The Laplace transform of Uz(x, t) + 2xut(x, t) is given as follows; L[Uz(x,t)] + 2x L[ut(x,t)] = L[2x]sU(x,s) - u(x,0) + 2x[sU(x,s)-u(x,0)] = 2x/sU(x,s) + 2x/s^2 - 1(2x/s)U(x,s) = 2x/s^2 - 1 + sU(x, s)U(x, s) = [2x/s^2 - 1]/[2x/s - s]U(x, s) = s(2x/s^2 - 1)/(2x - s^2) = s/(2x - s^2) - 1/(2(s^2 - 2x))
By using the inverse Laplace transform, we have; u(x, t) = [1/s] * e^(s^2t/2x) - (1/2)sinh(t sqrt(2x)) / sqrt(2x)
Thus, the solution to the given partial differential equation is given as follows; u(x, t) = [1/s] * e^(s^2t/2x) - (1/2)sinh(t sqrt(2x)) / sqrt(2x)Where, u(x,0) = 1 and u(0,t) = 1.
The integral transform known as the Laplace transform is particularly useful for solving ordinary differential equations that are linear. It finds extremely wide applications in var-ious areas of physical science, electrical designing, control engi-neering, optics, math and sign handling.
The mathematician and astronomer Pierre-Simon, marquis de Laplace, gave the Laplace transform its name because he used a similar transform in his work on probability theory.
Know more about Laplace transform:
https://brainly.com/question/30759963
#SPJ11
can someone please help

Answers
Answer:
I think its Your Values, but try and a get a second opinion
What’s the answer to 9 - x = 15 and -252 = 21k
Answers
Answer:
1)\(9 - x = 1\)
\(9-x-9=1-9\)
\(-x=-8\)
\(\cfrac{-x}{-1}=\cfrac{-8}{-1}\)
\(\boxed{x=8}\)
2)\(-252 = 21k\)
\(21k=-252\)
\(\cfrac{21k}{21}=\cfrac{-252}{21}\)
\(\boxed{k=-12}\)
Answer:
x= -6 k=-12
Step-by-step explanation:
15-9 is 6. 9+6=15 9-(-6)=15 because when two negatives are together they make a positive. (--)=+ K=-21 because -252/21 is -12.
Harvested apples from a farm in Eastern Washington are packed into boxes for shipping out to retailers. The apple shipping boxes are set to pack 45 pounds of apples. The actual weights of apples loaded into each box vary with mean µ = 45 lbs and standard deviation o 3 lbs. A) Is a sample of size 30 or more required in this problem to obtain a normally distributed sampling distribution of mean loading weights? O Yes Ο No B) What is the probability that 35 boxes chosen at random will have mean weight less than 44.55 lbs of apples? (Round 0 to two decimal places and your answer to four decimal places.) **Notes: DO NOT round any z-score.
Answers
A) No, a sample size of 30 or more is not required to obtain a normally distributed sampling distribution of mean loading weights in this problem. According to the Central Limit Theorem, when the sample size is sufficiently large (typically around 30 or more), the sampling distribution of the mean tends to be approximately normally distributed, regardless of the shape of the population distribution. In this case, since the population standard deviation is known (σ = 3 lbs), the sampling distribution of the mean will be normally distributed even with smaller sample sizes.
B) To calculate the probability that 35 boxes chosen at random will have a mean weight less than 44.55 lbs of apples, we need to standardize the mean weight using the Z-score and then find the corresponding probability from the standard normal distribution.
The Z-score is calculated using the formula:
Z = (X - µ) / (σ / √n)
X = 44.55 lbs (mean weight)
µ = 45 lbs (population mean)
σ = 3 lbs (population standard deviation)
n = 35 (sample size)
Substituting the values into the formula:
Z = (44.55 - 45) / (3 / √35)
Calculating Z, we can then find the corresponding probability using a standard normal distribution table or a calculator.
A) The Central Limit Theorem states that with a sufficiently large sample size, the sampling distribution of the mean tends to be normally distributed, regardless of the population distribution. However, in this case, since the population standard deviation is known, the sampling distribution of the mean will be normally distributed even with smaller sample sizes.
B) To calculate the probability, we standardize the mean weight using the Z-score formula and then find the corresponding probability from the standard normal distribution. This allows us to determine the probability of observing a mean weight less than 44.55 lbs of apples.
To know more about the Central Limit Theorem, refer here:
https://brainly.com/question/898534#
#SPJ11
What’s the sum for 1/6+square root 6
Answers
Answer:
1/6 +√6 = 2.6162
Step-by-step explanation:
Answer:
B:2.6161564...
Step-by-step explanation:
edge2020
If the mean of 25, 28, a, 30 and 32 is 27, then find the value of a.
Answers
Answer:
a = 20
Step-by-step explanation:
The mean is calculated as
mean = \(\frac{sum}{count}\)
= \(\frac{25+28+a+30+32}{5}\) = \(\frac{115+a}{5}\)
Then
\(\frac{115+a}{5}\) = 27 ( multiply both sides by 5 to clear the fraction )
115 + a = 135 ( subtract 115 from both sides )
a = 20
This proof shows the first five steps for verifying Use the drop-down boxes to complete the steps of the proof.
Answers
the drop-down boxes to complete the steps of the proof =
1. Tangent Half-angle identity
2. 1 + cos x
3. 1 - cos x
In mathematics, trigonometric functions are real functions that relate the angles of a right triangle to the ratio of the lengths of its two sides. They are widely used in all geometry-related sciences such as navigation, solid mechanics, celestial mechanics, and geodesy.
Trigonometric periodic functions repeat at predictable intervals, but are not a direct result of trigonometric functions. It can be used to accurately predict values outside the original range. Common non-trigonometric functions include: Four corners. triangle.
Learn more about trigonometric function here: https://brainly.com/question/6904750
#SPJ4
The question is incomplete. Please read below to find the missing content.
This proof shows the first five steps for verifying cot^2 (x/2)= cos x+1/cos c-1 use the drop-down boxes to complete the steps of the proof

The weights of tennis balls are normally distributed, with the mean being 5.15 ounces and the standard deviation being 0.10. what percentage of the balls weigh within one standard deviation of the mean?
Answers
The correct option is B.
Thus, 68% percentage of the balls weigh within one standard deviation of the mean.
What is the empirical formula rule?The Empirical Rule indicates that 99.7% of data that are observed to have a normal distribution fall within 3 standard deviations of the mean. According to this formula, 68 percent of the data are within one standard deviation, 95 percent are within two standard deviations, and 99.7 percent are within three standard deviations of the mean.
According to the empirical formula rule:Because approximately 68% of the data falls within a standard deviation of the mean, according to the empirical rule, 68% of the balls' weights fall within that range.
To know more about empirical formula rule visit:
https://brainly.com/question/1985421
#SPJ4
I understand that the question you are looking for is:
The weights of tennis balls are normally distributed, with the mean being 5.15 ounces and the standard deviation being 0.10. what percentage of the balls weigh within one standard deviation of the mean
A. 50%
B. 68%
C. 95%
D. 99.7%
Is (x + 6) a possible length of a rectangle if the area is x^2 + x − 30? Use an area model to prove your answer.
Can you use an area model to find the length and width of:
Answers
The answer is yes, (x + 6) is a possible length of a rectangle with area x² + x − 30.
To determine whether (x + 6) is a possible length of a rectangle with area x^² + x − 30, we can use an area model to visualize the situation.
First, we need to find the width of the rectangle.
The area of a rectangle is given by the formula A = lw,
where A is the area, l is the length, and w is the width.
We are given that the area is x² + x − 30, so we can set this equal to lw and solve for w:
x² + x − 30 = (x + 6)w
w = (x² + x − 30)/(x + 6)
The length of a rectangle must be greater than or equal to its width, so we need to check whether (x + 6) is greater than or equal to (x² + x − 30)/(x + 6). This simplifies to:
(x + 6) ≥ x² + x − 30
Expanding the left side and simplifying, we get:
x² + 12x + 36 ≥ x² + x − 30
11x ≥ -66
x ≥ -6
Since x must be a positive number (since we are dealing with lengths), we can conclude that (x + 6) is the possible length of the rectangle. Therefore, the answer is yes, (x + 6) is a possible length of a rectangle with an area x² + x − 30.
Learn more about Area here:
https://brainly.com/question/27683633
#SPJ1
Solve the following equation |2x+3|+|x-2|=6x
Answers
Recall the definition of absolute value:
• |x| = x if x ≥ 0
• |x| = -x if x < 0
So you need to consider 4 different cases (2 absolute value expressions with 2 possible cases each).
(i) Suppose 2x + 3 < 0 and x - 2 < 0. The first inequality says x < -3/2 and the second says x < 2, so ultimately x < -3/2. Then
|2x + 3| + |x - 2| = 6x
-(2x + 3) - (x - 2) = 6x
-2x - 3 - x + 2 = 6x
-3x - 1 = 6x
9x = -1
x = -1/9
But -1/9 is not smaller than -3/2, so this case provides no valid solution.
(ii) Suppose 2x + 3 ≥ 0 and x - 2 < 0. Then x ≥ -3/2 and x < 2, or -3/2 ≤ x < 2. Under this condition,
|2x + 3| + |x - 2| = 6x
(2x + 3) - (x - 2) = 6x
2x + 3 - x + 2 = 6x
x + 5 = 6x
5x = 5
x = 1
This solution is valid because it does fall in the interval -3/2 ≤ x < 2.
(iii) Suppose 2x + 3 < 0 and x - 2 ≥ 0. Then x < -3/2 or x ≥ 2. So
|2x + 3| + |x - 2| = 6x
-(2x + 3) + (x - 2) = 6x
-2x - 3 + x - 2 = 6x
-x - 5 = 6x
7x = -5
x = -5/7
This isn't a valid solution, because neither -5/7 < -3/2 nor -5/7 ≥ 2 are true.
(iv) Suppose 2x + 3 ≥ 0 and x - 2 ≥ 0. Then x ≥ -3/2 and x ≥ 2, or simply x ≥ 2.
|2x + 3| + |x - 2| = 6x
(2x + 3) + (x - 2) = 6x
2x + 3 + x - 2 = 6x
3x + 1 = 6x
3x = 1
x = 1/3
This is yet another invalid solution since 1/3 is smaller than 2.
So there is one solution at x = 1.
Geometric mean returns are: a simple averages of holding period returns. b expressed as compound rates of interest.c more applicable when no specific time interval is considered to be any more important than another. d widely used in statistical studies spanning very long periods of time.
Answers
The correct option is b expressed as compound rates of interest. Geometric mean returns are calculated by taking the nth root of the product of (1 + holding period return) for each period, where n is the number of periods.
The result is expressed as a compound rate of return, which reflects the compounding effect over time. Unlike arithmetic mean returns, which are simple averages of holding period returns, geometric mean returns give more weight to the returns in earlier periods and less weight to the returns in later periods. This makes geometric mean returns more applicable when no specific time interval is considered to be any more important than another.
Learn more about rates of interest.
https://brainly.com/question/28236069
#SPJ4
a. find the 30th percentile for the standard normal distribution b. find the 30th percentile for a normal distribution with mean 10 and std. dev. 1.5
Answers
a. To find the 30th percentile for the standard normal distribution, we first need to locate the z-score that corresponds to this percentile. We can use a standard normal distribution table or a calculator to find this value. From the table, we can see that the z-score that corresponds to the 30th percentile is approximately -0.524. Therefore, the 30th percentile for the standard normal distribution is z = -0.524.
b. To find the 30th percentile for a normal distribution with mean 10 and standard deviation 1.5, we can use the formula for transforming a standard normal distribution to a normal distribution with a given mean and standard deviation. This formula is:
z = (x - μ) / σ
where z is the standard normal score, x is the raw score, μ is the mean, and σ is the standard deviation.
To find the 30th percentile for this distribution, we first need to find the corresponding z-score using the formula above:
-0.524 = (x - 10) / 1.5
Multiplying both sides by 1.5, we get:
-0.786 = x - 10
Adding 10 to both sides, we get:
x = 9.214
Therefore, the 30th percentile for a normal distribution with mean 10 and standard deviation 1.5 is x = 9.214. This means that 30% of the observations in this distribution are below 9.214.
Learn more about z-score here
https://brainly.com/question/28000192
#SPJ11
The maximum area that is available for a rectangular garden is 80 square feet.
a. Write an inequality that represents the possible dimensions for the garden.
b. Find three different sets of allowable dimensions for the garden. Find
the area of each garden.
Answers
An inequality that represents the possible dimensions for the garden is ab < 80. And the three different sets of allowable dimensions for the garden are {5, 10}, {10, 5} and {6, 6} and the area 50 square feet, 50 square feet, 36 square feet respectively.
What is an inequality?In mathematics, "inequality" refers to a relationship between two expressions or values that are not equal to each other. To solve the inequality, you may multiply or divide each side by the same positive number, add the same amount to each side, take the same amount away from each side, and more. You must flip the inequality sign if you multiply or divide either side by a negative number.
Given:
The maximum area that is available for a rectangular garden is 80 square feet.
Let a and b are the length and width of the rectangular garden.
And A be the area.
(a).
So, A < 80
That means, ab < 80.
(b).
To find the dimension of the rectangle:
We find the numbers whose product is less than 80.
Let the three number sets are,
{5, 10}, {10, 5} and {6, 6}.
(c).
So, the area of the rectangles are:
5 x 10 = 50 square feet,
10 x 5 = 50 square feet,
And 6 x 6 = 36 square feet.
Therefore, the inequality is ab < 80, three number sets are {5, 10}, {10, 5} and {6, 6} and the area 50 square feet, 50 square feet, 36 square feet respectively.
To learn more about the inequality;
brainly.com/question/28823603
#SPJ1
Eva is working out the area of a triangle . The base is 7.8 and the length of one side is 6.3 cm. I multiply and then divide by two. What mistake has eva made?
Answers
Answer:
Eva used a side dimension instead of the height.
Step-by-step explanation:
The base needs to be multiplied by the height, then the result needs to be divided by 2. Eva's mistake is using a side dimension instead of the height. Her approach only works for a right triangle.
Eva multiplied the base by the side height, not the actual height.
Step-by-step explanation:
The area of a triangle is b×h×½, or b×h÷2. Eva multiplied the length times one side, as it says in the problem. The actual height of the triangle we don't know, but we know that Eva multiplied the base, 7.8 cm, by the wrong height.
Hope this helps! (Plz give me brainliest, it will help me achieve my next rank.)
Help needed ASAP will give brainliest and 5 star RATE

Answers
2 dogs, 4 horses 1 giraffe and a duck are lying on the bed. 3 chickens are flying over a chair. How many legs are on the ground?.
Answers
Four individuals have responded to a request by a blood bank for blood donations. None of them has donated
before, so their blood types are unknown. Suppose only type O is desired and only one of the four actually
has this type. If the potential donors are selected in random order for typing,
a) what is the probability that at least three individuals must be typed to obtain the desired type? (Hint:
it is the same as the event that the first and second are not of type O). B) What is the probability that the third is of type O? (Hint: that is, first isnot, second isnot, and the third
is. Use the generalized product rule)
Answers
The probability that at least three individuals must be typed to obtain the desired type is 1/2 and the probability that the third is of type O is 3/4
Probability is the event of occurances. Many of the events will not be predicted with the total certainty. Four individuals have responded to a request by a blood bank for blood donations. None of them has donated before, so their blood types are unknown.
Suppose only type O is desired and only one of the four actually has this type, and if the potential donors are selected in random order for typing,
The probability that the same as the event that the first and second are not of type O is 2/4 = 1/2
So, the probability that at least three individuals must be typed to obtain the desired type is 1/2
The probability that is, first is not, second is not, and the third is 3/4
So, the probability that the third is of type O is 3/4
Therefore, the probability that at least three individuals must be typed to obtain the desired type is 1/2 and the probability that the third is of type O is 3/4
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ4
Solve.
3 3/5 x (-8 1/3) = ?
Answers
Step-by-step explanation:
1. 3 3/5 × (-8 1/3)
2. 18/5 × -25/3
3. 18/5 × -25/3 = -90/3
Ans. -30
Find the slope of the line using rise over run

Answers
Answer: 1
Step-by-step explanation:
For every three its going down, its going three to the left.
So it's going -3/-3
OR
-1/-1 = 1/1 = 1
In a Cartesian coordinate system for a three-dimensional space.
Sphere (S) is represented by equation: \((x-1)^2+(y+2)^2+(z-3)^2=25\).
Plane (P) is represented by equation: \(x+2y-2z+1=0\).
Line (d) is parallel to (P), passes through the origin and passes through (S) at two separate points A & B. Find the maximum length of AB.
Answers
In a Cartesian coordinate system for a three-dimensional space, let the sphere S be represented by the equation:
(x - a)^2 + (y - b)^2 + (z - c)^2 = r^2
where (a, b, c) are the coordinates of the center of the sphere, and r is the radius.
Let the plane P be represented by the equation:
Ax + By + Cz + D = 0
where (A, B, C) is the normal vector to the plane.
Since the line d is parallel to P and passes through the origin, it can be represented by the equation:
lx + my + nz = 0
where (l, m, n) is a vector parallel to the plane P.
To find the intersection points of the sphere S and the line d, we can substitute the equation of the line into the equation of the sphere, which gives us a quadratic equation in t:
(lt - a)^2 + (mt - b)^2 + (nt - c)^2 = r^2
Expanding this equation and collecting terms, we get:
(l^2 + m^2 + n^2) t^2 - 2(al + bm + cn) t + (a^2 + b^2 + c^2 - r^2) = 0
Since the line d passes through the origin, we have:
l(0 - a) + m(0 - b) + n(0 - c) = 0
which simplifies to:
al + bm + cn = 0
Therefore, the quadratic equation reduces to:
(l^2 + m^2 + n^2) t^2 + (a^2 + b^2 + c^2 - r^2) = 0
This equation has two solutions for t, which correspond to the two intersection points of the line d and the sphere S:
t1 = -(a^2 + b^2 + c^2 - r^2) / (l^2 + m^2 + n^2)
t2 = -t1
The coordinates of the intersection points can be obtained by substituting these values of t into the equation of the line d:
A = lt1, B = mt1, C = nt1
and
D = lt2, E = mt2, F = nt2
To find the distance between A and B, we can use the distance formula:
AB = sqrt((A - D)^2 + (B - E)^2 + (C - F)^2)
To maximize this distance, we can differentiate the distance formula with respect to t1 and set the derivative equal to zero:
d/dt1 (AB)^2 = 2(A - D)l + 2(B - E)m + 2(C - F)n = 0
This equation represents the condition that the direction vector (A - D, B - E, C - F) is orthogonal to the line d. Therefore, the vector (A - D, B - E, C - F) is parallel to the normal vector (l, m, n) of the plane P.
Using this condition, we can find the values of t1 and t2 that correspond to the maximum distance AB. Then we can substitute these values into the distance formula to find the maximum length of AB.
the parallelogram in quadrant ii is the image of the parallelogram in quadrant i after a counterclockwise rotation about the origin.what is the angle of rotation?
Answers
the angle of rotation is 180°. The parallelogram in quadrant I is the image of the parallelogram in quadrant II after a counterclockwise rotation about the origin.
The angle of rotation is 180°.
The parallelogram in quadrant I is the image of the parallelogram in quadrant II after a counterclockwise rotation about the origin. This means that the parallelogram in quadrant I has been rotated 180° (a full circle) relative to the parallelogram in quadrant II. Thus, the angle of rotation is 180°.
Learn more about angle here
https://brainly.com/question/28451077
#SPJ4
If f(x) = 2x³ + x - -4, then what is the remainder when f(x) is divided by x - 3?
Answers
Answer:
61
Step-by-step explanation:

HELP PLEASEEE OVERDUE (show work) will give BRAINLIEST ! :)
Answers
Answer:
2/7 I Don't know the other one
here you go, hope that helps some
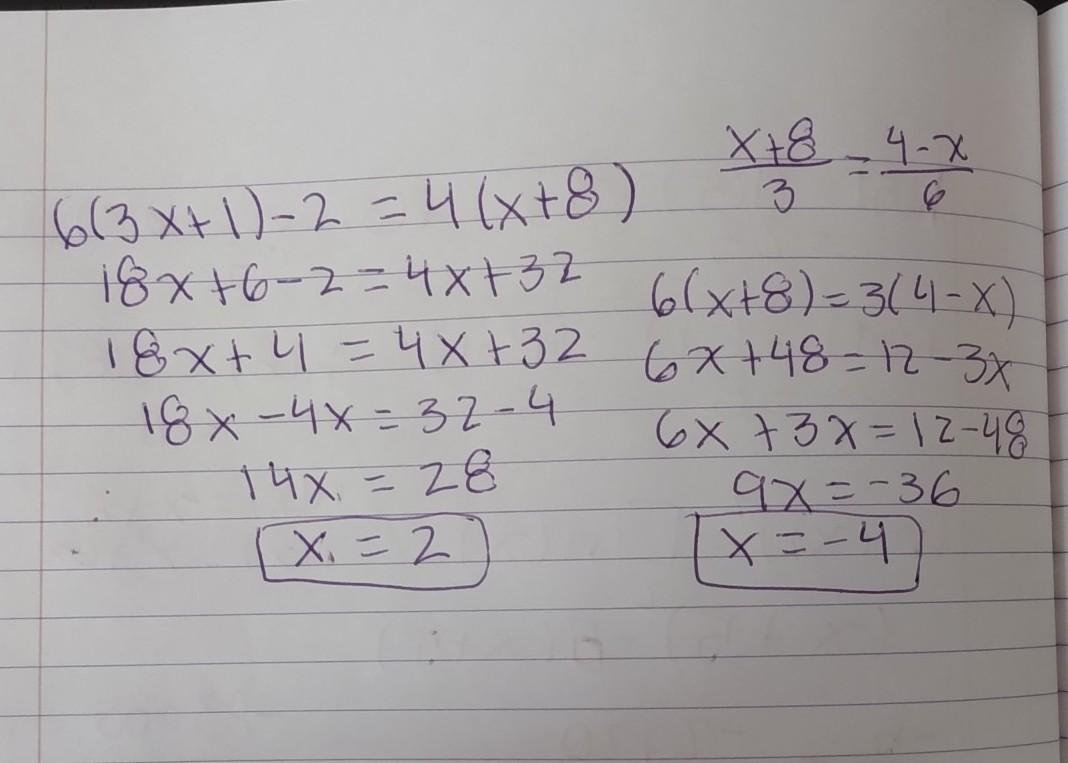
PLEASE help me with this question! No nonsense answers and answer with full solutions please!


Answers
Answer: b) {-3, 0.5}
Step-by-step explanation:
The new equation is the original equation plus 6. Move the original graph UP 6 units. The solutions are where it crosses the x-axis.
\(\text{Original equation:}\quad f(x)=\dfrac{15}{x}-\dfrac{9}{x^2}\\\\\\\text{New equation:}\quad\dfrac{15}{x}+6=\dfrac{9}{x^2}\\\\\\.\qquad \qquad f(x)= \dfrac{15}{x}-\dfrac{9}{x^2}+6\)
+6 means it is a transformation UP 6 units.
Solutions are where it crosses the x-axis.
The curve now crosses the x-axis at x = -3 and x = 0.5.

La densidad del etanol es 0.79 gr/ml. Calcula la masa del etanol 25.7 ml del etanol.
Answers
Answer:
If you didn't know what the question was, here is the translation:
The ethanol density is 0.79 gr / ml. Calculate the mass of ethanol 25.7 ml of ethanol.
a characteristic, usually a numerical value, which describes a sample is called a _______. a. parameter b. statistic C. constant d. variable
Answers
Answer: B. statistic
Step-by-step explanation: A characteristic, usually a numerical value, which describes a sample, is called a statistic.
1) a. Write an equation that expresses the first law of thermodynamics in terms of heat and work.
b. Under what conditions will the quantities q and w be negative numbers?
Answers
The first law of thermodynamics is a fundamental principle in physics that states energy cannot be created or destroyed, only converted from one form to another. It can be expressed in terms of heat and work through the equation:
ΔU = q - w
where ΔU represents the change in internal energy of a system, q represents the heat added to the system, and w represents the work done on or by the system.
Now, let's address when the quantities q and w would be negative numbers.
1) When q is negative: This occurs when heat is removed from the system, indicating an energy loss. For example, when a substance is cooled, heat is extracted from it, resulting in a negative value for q.
2) When w is negative: This occurs when work is done on the system, decreasing its energy. For instance, when compressing a gas, work is done on it, leading to a negative value for w.
In both cases, the negative sign indicates a reduction in energy or the transfer of energy from the system to its surroundings.
In summary, the first law of thermodynamics can be expressed as ΔU = q - w, and q and w can be negative numbers when energy is lost from the system through the removal of heat or when work is done on the system.
know more about first law of thermodynamics states.
https://brainly.com/question/31275352
#SPJ11