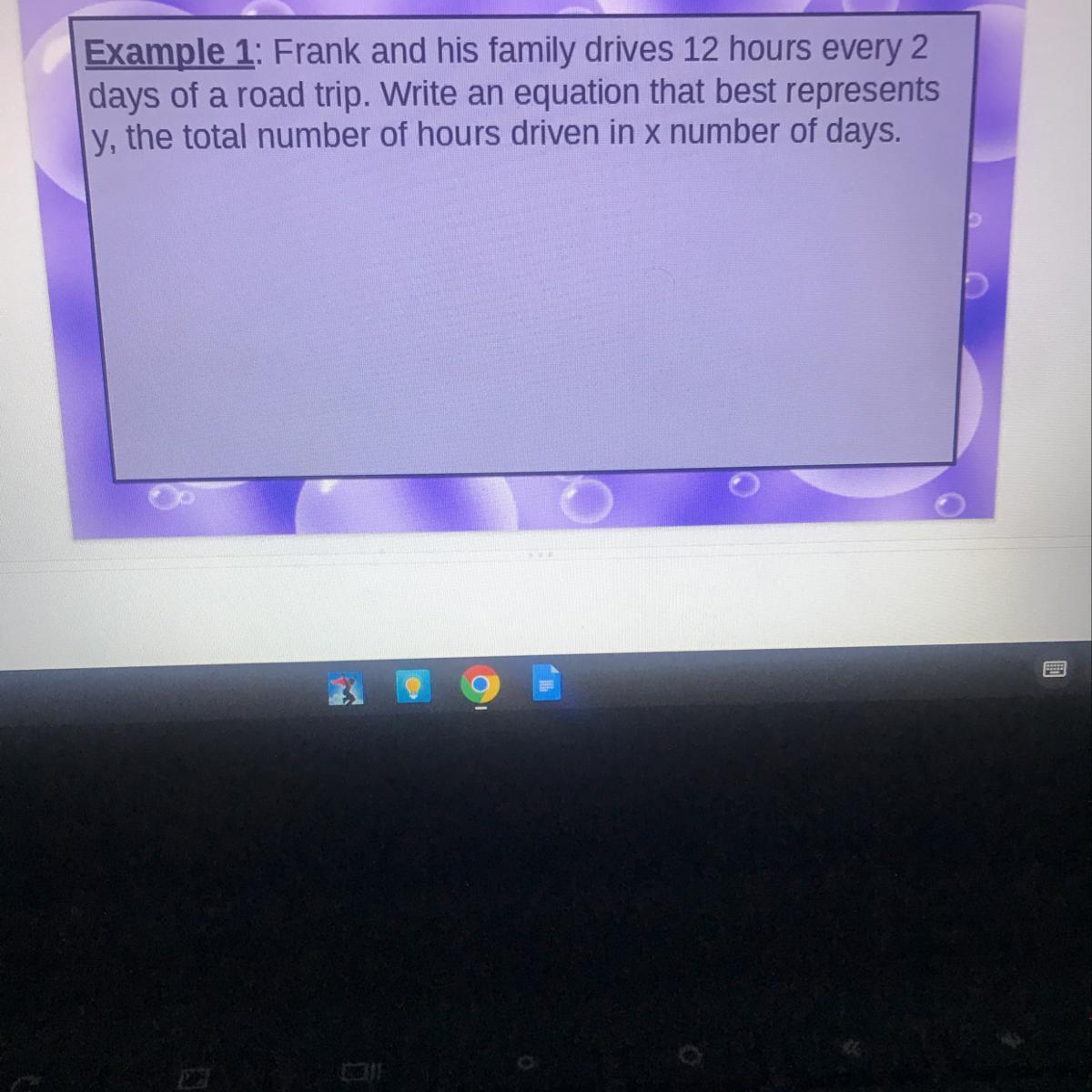
5.) Joey is saving money for a car that will cost at least $2500. His grandpa gave him. $460 and he is currently saving $15 each week. Write and solve an inequality to represent the number of weeks it will take Joey to save up for his car. ​

This occurs when the number of $5 price increases is approximately 10.82 or 15.32.

The function given is P(x) = −6x2 + 156x + 1,000, where x is the number of $5 price increases for each solar panel. We are to identify the approximate value of the x-intercept and explain what the x-intercept means in terms of the problem scenario.

The x-intercept is a point where the graph of the function crosses the x-axis. At this point, the value of the function is zero.

We can find the x-intercept by setting P(x) = 0 and solving for x.0 = −6x2 + 156x + 1,0006x2 - 156x - 1000 = 0Dividing by 6, we get:x2 - 26x - 166.67 = 0Solving using the quadratic formula,

we get:x ≈ 10.82 or x ≈ 15.32So, the x-intercepts are approximately 10.82 and 15.32. In terms of the problem scenario, the x-intercept represents the point at which the company breaks even, i.e., the point at which the daily profit is zero.

To learn more about : price

https://brainly.com/question/1153322

#SPJ8

The interval of the graph at which Susan is running fastest is from point A ( 0 , 0 ) to B ( 10 , 3 )

Given data ,

Susan is running a 5k race. The graph of distance vs. time is shown

So , the slope of the first line is m₁

And , the slope of the second line is m₂

where the points are A ( 0 , 0 ) , B ( 10 , 3 ) , C ( 20 , 4 )

Now , slope of AB is

m₁ = ( 3/10 ) = 0.3

And , m₁ = 0.3 kilometers per minute

And , slope of BC is

m₂ = ( 4 - 3 ) / ( 20 - 10 )

m₂ = 1/10

m₂ = 0.1 kilometers per minute

Therefore , the interval is fastest at second line from B ( 10 , 3 ) , C ( 20 , 4 )

Hence , Susan is running fastest is from point A ( 0 , 0 ) to B ( 10 , 3 )

To learn more about equation of line click :

https://brainly.com/question/14200719

#SPJ1

Answer:

I think it's D

Step-by-step explanation:

The number never goes over 0 so there is no need to put anything above 0

Answer:

the answer is D. The second arrow he drew should have started at -15 instead of 0.

Step-by-step explanation:

was on a test I took and got 100

Answer:

True

Step-by-step explanation:

The easiest way to understand this problem is to first breakdown the notation. In words, the problem is stating 9 is NOT an element of the set containing the elements 4, 1, 8, and 7. Since 4\(\neq\)9, 1\(\neq\)9, 8\(\neq\)9, and 7\(\neq\)9 then 9 is not an element of this set and the statement is true.

The value of function f (4) is,

⇒ f (4) = 19

We have to given that;

The function is,

⇒ f (x) = x² + 3

Now, WE can find the value of f (4) by substitute x = 4 in above function as,

⇒ f (x) = x² + 3

Plug x = 4;

⇒ f (4) = 4² + 3

⇒ f (4) = 16 + 3

⇒ f (4) = 19

Thus, The value of function f (4) is,

⇒ f (4) = 19

Learn more about the function visit:

https://brainly.com/question/11624077

#SPJ1

The number of apples(x) and bananas (y) that Alonso bought at the grocery store is x = 6 and y = 5.  

To find an unknown quantity we use Linear equations. Here we use variables like a, b, c... x, y, z, etc. to represent the unknown number.

By using different variables we need to make equations according to the condition given problem and solve the equation for the value of variables.  

Here we have

Alonso bought $ 14 worth of apples and bananas

The cost of each Apple = $ 1.75

The cost of each banana = $ 0.70  

Let's assume that Alonso bought 'x' apples and 'y' bananas  

Given that the total of Apples and Bananas = 11  

=> x + y = 11 ----- (1)

The cost f x apples = 1.75 × x = 1.75x

The cost of y bananas = 0.70 × y = 0.70y  

Given the total worth,  1.75x + 0.70y = 14 ---- (2)  

=>   x + 0.4y = 8 ------ (2)

Now solve (1) and (2) for x and y values

Do (1) - (2)

=>  x + y - x - 0.4y = 11 - 8

=>  0.6y = 3

Multiply with 10 on both sides

=> 6y = 30

Divide by 6 into both sides

=> y = 5  

Now substitute y = 5 in (1)

=> x + 5 = 11

=> x = 6

Therefore,

The number of apples(x) and bananas (y) that Alonso bought at the grocery store is x = 6 and y = 5.

Learn more about Linear Equations at

https://brainly.com/question/11897796

#SPJ1

The number she'd have is:

Explanation:

First, let's see which number is in the tens place and which number is in the ones place (the units place).

In the number 548, the place value of 5 is hundreds, the place value of 4 is tens, and the place value of 8 is ones (or units).

So if Sera adds two to the units, she'll have 10. But, since we can't write the number as 5410 (that would be a totally different number), we just write 0 in the units place, and shift 1 to the tens place, which gives us :

550

That's not all, since we also add 1 to the tens:

560

The Propositions are resulting

(a) ∀x∃y(x = y²) is False

(b) ∀x∃y(x² = y) is True.

(c) ∃x∀y(xy = 0) is True.

(d) ∀x∃y(x + y = 1) is True.

(a) ∀x∃y(x = y²)

This proposition states that for every x, there exists a y such that x is equal to y². To determine the truth value, we need to check if this statement holds true for every value of x.

If we take any positive value for x, we can find a corresponding value of y that satisfies the equation.

For example, if x = 4, then y = 2 satisfies the equation since 4 = 2². Similarly, if x = 9, then y = 3 satisfies the equation since 9 = 3².

Therefore, the proposition (a) is false.

(b) ∀x∃y(x² = y)

For any given positive or negative value of x, we can find a corresponding value of y that satisfies the equation.

For example, if x = 4, then y = 2 satisfies the equation since 4² = 2. Similarly, if x = -4, then y = -2 satisfies the equation since (-4)² = -2.

Therefore, the proposition (b) is true.

(c) ∃x∀y(xy = 0)

The equation xy = 0 can only be satisfied if x = 0, regardless of the value of y. Therefore, there exists an x (x = 0) that makes the equation true for every y.

Therefore, the proposition (c) is true.

(d) ∀x∃y(x + y = 1)

To determine the truth value, we need to check if this statement holds true for every value of x.

If we take any value of x, we can find a corresponding value of y that satisfies the equation.

For example, if x = 2, then y = -1 satisfies the equation since 2 + (-1) = 1. Similarly, if x = 0, then y = 1 satisfies the equation since 0 + 1 = 1.

Therefore, the proposition (d) is true.

Learn more about Proposition here:

https://brainly.com/question/30695879

#SPJ1

Answer:

simple even tho im in 6th grade it would be over $100

Answer:d

Step-by-step explanation:

Answer:

a1 = 3, a2 = 6, a3 = 11, and a10 = 102

Step-by-step explanation:

n² + 2

a1 = (1)² + 2

= 1 + 2

= 3

a2 = (2)² + 2

= 4 + 2

= 6

a3 = (3)² + 2

= 9 + 2

= 11

a10 = (10)² + 2

= 100 + 2

= 102

PLEASE MARK ME AS BRAINLIEST AND HAVE A NICE DAY :)

You have to write the equation for a line that crosses the point (-4, -7) and is perpendicular to the line

When you have to determine a line that is perpendicular to a known line, you have to keep in mind that the slope of the perpendicular line will be the negative inverse of the first one.

If for exampla you have two lines, the first one being:

And the second one, that is perpedicular to the one above:

The slope of the second one is the negative inverse of the first one:

The slope of the given line y=-7/4+4 is m=-7/4

So the slope of the perpendicular line has to ve the inverse negative of -7/4

Considering it has to pass through the point (-4,-7) and that we already determined its slope, you can unse the point slope formula to determine the equation of the perpendicular line:

replace with the coordinates of the point and the slope and calculate:

Subtract 7 to both sides of the equation to write it in slope-intercept form:

Now you can graph both lines

Time would be taken by them  if they worked together is  1 .875 hours .

Work is the effort applied to produce a deliverable or accomplish a task. A certain amount of time (T) is taken to complete a certain work (W).

Work Done = Time Taken × Rate of Work.

Rate of Work = 1 / Time Taken.

Time Taken = 1 / Rate of Work.

According to the question

Fred takes 3 hours to dig a garden.

Rate of Work of Fred to dig a garden = 1 / Time Taken.

                                                                = 1/ 3

Jason 5 hours to dig a garden.

Rate of Work of Jason to dig a garden = 1 / Time Taken.

                                                                 = 1/5

Now, Time taken by them if they work together  

Work Done = Time Taken × Rate of Work.

Let time taken be t

\(\frac{t}{3} + \frac{t}{5} = 1\)

\(\frac{8t}{15} = 1\)

t = \(\frac{15}{8}\)

t = 1 .875 hours

Hence,  Time would be taken by them  if they worked together is  1 .875 hours .

To know more about  work and time relationship here:

https://brainly.com/question/3854047

#SPJ2

Answer:

\( - 38 {p}^{2} - 78p \\ p = - 1 \\ - 38 \times { (- 1)}^{2} - 78 \times - 1 \\ - 38 + 78 \\ = 40 \\ thank \: you\)

Adding p = -1

\( - 38( - 1) {}^{2} - 78( - 1) \\ - 38 \times 1 - ( - 78) \\ ( - 38) - ( - 78) \\ - 38 + 78 \\ = 40\)

Answer:

Part A:

To find the percentage of survey respondents who liked neither hamburgers nor burritos, we need to calculate the frequency in the "Does not like hamburgers" and "Does not like burritos" categories.

Frequency of "Does not like hamburgers" = Total in "Does not like hamburgers" category = 135

Frequency of "Does not like burritos" = Total in "Does not like burritos" category = 54

Total respondents who liked neither hamburgers nor burritos = Frequency of "Does not like hamburgers" + Frequency of "Does not like burritos" = 135 + 54 = 189

Percentage of survey respondents who liked neither hamburgers nor burritos = (Total respondents who liked neither hamburgers nor burritos / Total respondents) x 100

Percentage = (189 / 205) x 100 = 92.2%

Therefore, 92.2% of the survey respondents liked neither hamburgers nor burritos.

Part B:

To find the marginal relative frequency of all customers who like hamburgers, we need to divide the frequency of "Likes hamburgers" by the total number of respondents.

Frequency of "Likes hamburgers" = 110 (given)

Total respondents = 205 (given)

Marginal relative frequency = Frequency of "Likes hamburgers" / Total respondents

Marginal relative frequency = 110 / 205 ≈ 0.5366 or 53.66%

Therefore, the marginal relative frequency of all customers who like hamburgers is approximately 53.66%.

Part C:

To determine if there is an association between liking burritos and liking hamburgers, we can compare the joint and marginal frequencies.

Joint frequency of "Likes hamburgers" and "Likes burritos" = 29 (given)

Marginal frequency of "Likes hamburgers" = 110 (given)

Marginal frequency of "Likes burritos" = 70 (calculated by adding the frequency of "Likes burritos" in the table)

To assess the association, we compare the ratio of the joint frequency to the product of the marginal frequencies:

Ratio = Joint frequency / (Marginal frequency of "Likes hamburgers" x Marginal frequency of "Likes burritos")

Ratio = 29 / (110 x 70)

Ratio ≈ 0.037 (rounded to three decimal places)

Answer:

12y x 2x

Step-by-step explanation:

To answer this question, we have that:

Then, we have that:

And we cannot simplify this expression anymore. Therefore,

Answer: 26129.6

Step-by-step explanation:

6721 x 381 = 2560701

14 + 84 = 98

2560701  / 98 = 26129.6

Answer:

work is shown and pictured

Step-by-step explanation:

Note that t = d/r where t is time, d is distance, and r is rate/speed.

We can come up with two equations with the information given and the equation:

t_1 hr = (10 km)/(x km/hr)

t_2 hr = (12 km)/(x - 1 km/hr)

where t_1 is the time taken to run the 10km the first day and t_2 is the time taken to run the 12km the second day.

We know that 30 minutes is 1/2 of an hour and that t_1 is 30 minutes less than t_2 (as stated in the question). Therefore, we can write:

t_1 = t_2 - 1/2

Substituting the values we derived:

(10 km)/(x km/hr) = (12 km)/(x - 1 km/hr) -1/2

Then we can evaluate by multiplying by 2x(x-1) on both sides:

20(x-1) = 24x - (x)(x-1)

20x - 20 = 24x - x^2 + x

x^2 -5x -20 = 0

And we are done.

I hope this helps! :)

An equation is formed when two equal expressions. The equation for the time can be written as (12/x-1)-(10/x)=0.5. The value of x is 7.623.

An equation is formed when two equal expressions are equated together with the help of an equal sign '='.

A.) Given Alfonso runs 10 km at an average speed of x km/h. Therefore, the time taken by Alfonso to rum 10km is 10/x hour.

Also, The next day he runs 12 km at an average speed of (x - 1) km/h. Therefore, the time taken by Alsonso to run 12km is 12/(x-1) hour.

Now, the time taken for the 10km run in 30minutes(0.5 hours) is less than the time taken for the 12 km run. Therefore, we can write,

\(\dfrac{12}{(x-1)}-\dfrac{10}{x} =0.5\)

The equation for the time can be written as (12/x-1)-(10/x)=0.5.

B.) The value of x can be written as,

\(\dfrac{12}{(x-1)}-\dfrac{10}{x} =0.5\\\\12x-10(x-1)=0.5 \times x \times (x-1)\\\\12x - 10x +10 = 0.5x^2-0.5x\\\\2x+10 = 0.5x^2-0.5x\\\\0=0.5x^2 - 2.5x -10\\\\x = -2.623, 7.623\)

Since the time can not be negative. Hence, the value of x is 7.623.

Learn more about Equation:

https://brainly.com/question/2263981

#SPJ2

Answer:

Step-by-step explanation:

We can use the method of undetermined coefficients to solve this differential equation. First, we will need to find the solution to the homogeneous equation and the particular solution to the non-homogeneous equation.

For the homogeneous equation, we will use the form y"+ky=0, where k is a constant. We can find the solutions to this equation by letting y=e^mx,

y"=m^2e^mx -> (m^2)e^mx+k*e^mx=0, therefore (m^2+k)e^mx=0

(m^2+k) should equal 0 for the equation to have a non-trivial solution. Therefore, m=±i√(k), and the general solution to the homogenous equation is y=A*e^i√(k)x+Be^-i√(k)*x.

Now, we need to find the particular solution to the non-homogeneous equation. We can use the method of undetermined coefficients to find the particular solution. We will let yp=a0+a1x+a2x^2+.... As the derivative of a sum of functions is the sum of the derivatives, we get

yp″=a1+2a2x....yp‴=2a2+3a3x+....

Substituting the general solution into the non-homogeneous equation, we get

a0+a1x+a2x^2+...+2a2x+3a3x^2+...=Y(4)

So, the coefficient of each term in the expansion of the left hand side should equal the coefficient of each term in the expansion of the right hand side. Since there is only one term on the right hand side, we get the recurrence relation:

a(n+1)=Y(n-2)/n^2

From this relation, we can find all the coefficients in the expansion for the particular solution. Using this particular solution, we can find the total solution to the differential equation as the sum of the homogeneous solution and the particular solution.

Answer:

134,000-X=Y

Step-by-step explanation:

you'll first have to solve how many categories there are, but since we don't know we'll use X, we already know that there is 134,000 books, but we don't know how many books are reference or other, so we use Y to represent that.

so it's

134,000-X=Y

I hope this helps

\(f(x)=2(3)^{x+1} \\\\[-0.35em] ~\dotfill\\\\ f(2)=2(3)^{(2)+1}\implies f(2)=2(3)^3\implies f(2)=2(3^3) \\\\\\ f(2)=2(27)\implies f(2)=54\)

Answer:

Exact form:4/15

decimal form: 0.26(6 is repeating)

Step-by-step explanation:

Isolate the variable by dividing each side by factors that don't contain the variable.

If the sum of the length and width of rectangle is 60 and rectangle is having maximum area then the dimensions are 30 units each.

Given that the sum of length and breadth of rectangle is 60.

We are required to find the dimensions of the rectangle that will have the maximum area. Area is basically how much part of surface is being covered by that particular shape or substance.

Let the length of rectangle be x.

According to question the breadth will be (60-x).----2

Area of rectangle=Length *Breadth

A=x(60-x)

A=60x-\(x^{2}\)

Differentiate A with respect to x.

dA/dx=60-2x

Again differentiate with respect to x.

\(d^{2} A/dA^{2}\)=-2x

-2x<0

So the area is maximum because x cannot be less than or equal to 0.

Put dA/dx=0

60-2x=0

60=2x

x=30

Put the value of x in 2 to get the breadth.

Breadth=60-x

=60-30

=30

Hence if the sum of the length and width of rectangle is 60 and rectangle is having maximum area then the dimensions are 30 units each.

Learn more about differentiation at https://brainly.com/question/954654

#SPJ1

The 99.7% confidence interval for the true proportion of teachers who provide extra credit is 0.21 to 0.33.

Number is a mathematical concept used to quantify a particular quantity or amount, or to name a specific object or entity. It is used in a variety of ways such as counting, measuring, comparing, estimating, and expressing mathematical relationships. Numbers are used for counting, measuring, and many other operations. Numbers can be expressed in numeric form, such as 1, 2, 3; in algebraic form, such as x^2-3x+2; or in symbolic form, such as √2. Numbers can also be used to represent functions or variables.

A 99.7% confidence interval for the true proportion of teachers who provide extra credit can be calculated as:

p′ ± 3σp′ = 0.27 ± (3 × 0.03) = 0.21 to 0.33

This confidence interval indicates that the true proportion of teachers who provide extra credit is between 0.21 and 0.33 with a 99.7% confidence level. That is, there is a 99.7% probability that the true proportion of teachers who provide extra credit is between 0.21 and 0.33.

The confidence interval for the true proportion of teachers who provide extra credit is determined by calculating the sample proportion (p′), sampling standard deviation (σp′), and the critical value of the normal distribution (Zc), which is the number of standard deviations from the mean that the sample proportion is likely to be. In this case, the critical value of the normal distribution is 3, because a 99.7% confidence level corresponds to a Z-score of 3. The confidence interval is calculated by adding and subtracting the critical value multiplied by the standard deviation from the sample proportion.

This confidence interval is an estimate of the true proportion of teachers who provide extra credit, and it can be used to make decisions or predictions about the population proportion. For example, a school administrator may use the confidence interval to determine the likely proportion of teachers who provide extra credit and make decisions about how to allocate resources.

In conclusion, the 99.7% confidence interval for the true proportion of teachers who provide extra credit is 0.21 to 0.33. This confidence interval is an estimate of the true proportion of teachers who provide extra credit, and it can be used to make decisions or predictions about the population proportion.

To know more about number click-
http://brainly.com/question/24644930
#SPJ1

The 99.7% confidence interval for the true proportion of teachers who provide extra credit is 0.21 to 0.33.

What is number?

Number is a mathematical concept used to quantify a particular quantity or amount, or to name a specific object or entity. It is used in a variety of ways such as counting, measuring. comparing, estimating, and expressing mathematical relationships. Numbers are used for counting, measuring, and many other operations. Numbers can be expressed in numeric form, such as 1, 2, 3; in algebraic form, such as x^2-3x+2; or in symbolic form, such as √2. Numbers can also be used to represent functions or variables.

A 99.7% confidence interval for the true proportion of teachers who provide extra credit can be calculated as:

p' ± 3op' = 0.27 ±(3 x 0.03) 0.21 to 0.33

This confidence interval indicates that the true proportion of teachers who provide extra credit is between 0.21 and 0.33 with a 99.7% confidence level. That is, there is a 99.7% probability that the true proportion of teachers who provide extra credit is between 0.21 and 0.33.

The confidence interval for the true proportion of teachers who provide extra credit is determined by calculating the sample proportion (p'), sampling standard deviation (op'), and the critical value of the normal distribution (Zc), which is the number of standard deviations from the mean that the sample proportion is likely to be. In this case, the critical value of the normal distribution is 3, because a 99.7% confidence level corresponds to a Z-score of 3. The confidence interval is calculated by adding and subtracting the critical value multiplied by the standard deviation from. the sample proportion.

This confidence interval is an estimate of the true proportion of teachers who provide extra credit, and it can be used to make decisions or predictions about the population proportion. For example, a school administrator may use the confidence interval to determine the likely proportion of teachers who provide extra credit and make decisions about how to allocate resources.

In conclusion, the 99.7% confidence interval for the true proportion of teachers who provide extra credit is 0.21 to 0.33. This confidence interval is an estimate of the true proportion of teachers who provide extra credit, and it can be used to make decisions or predictions about the population proportion.

Learn more about confidence interval here,

https://brainly.com/question/20309162

#SPJ1