45 points150 falls between what two integers?-25 and -75-2.3 and -3-13 and -12-12 and -11
Answers
First of all, is is necessary to calculate the square root of 150:
√150 = √(6*25) = 5√6
√6 ≈ 2.44
then, you have:
-√150 = -5√6 = -5(2.44) = -12.2
Then, -√150 is in between -13 and -12
Related Questions
When a number is decreased by 20% of itself, the result is 96. What is the number?
The number is
Answers
Answer:
480
Step-by-step explanation:
Take 96 and divide it by 2 to get what ten percent would be: 48
Then just multiply 48 by ten for 100% (The number): 480.
To check, take a calculator and do 480-20% and it equals 96.
We took away 20% of the original number, so we are left with 80% of the original number.
So we can say 80% = 96
Divide both sides by 80 to get 1%
And we get 1% = 1.2
And then multiply both sides by 100 to get 100% (aka, original number)
100% = 120 :)
Work out the volume of the prism height of 12 4 and five
Answers
The calculated volume of the prism is 702 cubic cm
Finding the volume of the prismFrom the question, we have the following parameters that can be used in our computation
The trapezoidal prism (see attachment)
The formula of the volume of a trapezoidal prism is
Volume = Base area * Height
Where we have
Base area = 1/2 * (8 + 10) * 6
Evaluate the sum of 8 and 10
Base area = 1/2 * 18 * 6
Evaluate the products of 1/2, 18 and 6
Base area = 54
Also, we have
Height = 13
So, the volume is calculated as
volume = 13 * 54
Evaluate
volume = 702
Hence, the volume of the prism is 702 cubic cm
Read more about volume at
brainly.com/question/463363
#SPJ1

Which expression is equivalent to StartRoot 8 x Superscript 7 Baseline y Superscript 8 Baseline EndRoot? Assume x greater-than-or-equal-to 0.
x y squared StartRoot 8 x cubed EndRoot
2 x cubed y cubed StartRoot x y squared EndRoot
2 x cubed y Superscript 4 Baseline StartRoot 2 x EndRoot
4 x cubed y Superscript 4 Baseline StartRoot x EndRoot
Answers
The expression that is equivalent to StartRoot \(8 x^7 y^8\) EndRoot is (\(2 x^3 y^4\) StartRoot 2 x EndRoot)^2.
To understand why this is the case, let's break down each expression and simplify them step by step:
StartRoot \(8 x^7 y^8\) EndRoot:
We can rewrite 8 as \(2^3\), and since the square root can be split over multiplication, we have StartRoot \((2^3) x^7 y^8\) EndRoot. Applying the exponent rule for square roots, we get StartRoot \(2^3\) EndRoot StartRoot \(x^7\) EndRoot StartRoot \(y^8\) EndRoot.
Simplifying further, we have 2 StartRoot \(2 x^3 y^4\) EndRoot StartRoot \(2^2\) EndRoot StartRoot \(x^2\) EndRoot StartRoot \(y^4\) EndRoot. Finally, we obtain 2 \(x^3 y^4\) StartRoot 2 x EndRoot, which is the expression in question.
(\(2 x y^2\) StartRoot 8 x^3 EndRoot)^2:
Expanding the expression inside the parentheses, we have \(2 x y^2\)StartRoot \((2^3) x^3\) EndRoot. Applying the exponent rule for square roots, we get \(2 x y^2\) StartRoot \(2^3\) EndRoot StartRoot \(x^3\) EndRoot.
Simplifying further, we have \(2 x y^2\) StartRoot 2 x EndRoot. Squaring the entire expression, we obtain (\(2 x y^2\) StartRoot 2 x EndRoot)^2.
Therefore, the expression (\(2 x^3 y^4\) StartRoot 2 x EndRoot)^2 is equivalent to StartRoot \(8 x^7 y^8\) EndRoot.
For more such questions on expression
https://brainly.com/question/1859113
#SPJ8
A quadrilateral is shown.
H
6.5
5.51
What is the area of the quadrilateral? Enter the answer in the box.
Answers
The calculated area of the quadrilateral is 35.82 square units.
What is the area of the quadrilateral?Given that
BAse = 6.5
Height = 5.51
To find the area of a quadrilateral, we need to multiply the base by the height.
Area of quadrilateral = base x height
Substituting the given values, we get:
Area = 6.5 x 5.51
Area = 35.815
Rounding to the nearest hundredth, the area of the quadrilateral is 35.82 square units.
Read more about area at
https://brainly.com/question/24487155
#SPJ1
HELP HELP HELP
A park is in the shape of a rectangle 8 miles long and 6 miles wide. How much shorter is your walk if you walk diagonally across the park than along the two sides of it? Round to the nearest tenth if necessary.
Answers
The absolute value of this difference is 18 miles, so the walk diagonally across the rectangle park is approximately 18 miles shorter than walking along the two sides of it.
What is rectangle ?A rectangle is just a square with four perpendicularly in the Euclidean plane. An equiangular quadrant or a quadrant that appears to have identical angles are other names for it. A straight angle is another choice for the parallelogram. A square has four edges that are the same length. Quadrilaterals with four equal edges and four 90° edges are called rectangles. As a consequence, it is occasionally referred to as a "equirectangular square".
Here,
The length of the diagonal of the rectangle can be found using the Pythagorean theorem:
d = √(8^2 + 6^2) ≈ 10
So the length of the diagonal is approximately 10 miles.
To find the distance of walking along the two sides of the rectangle, we can use the formula for the perimeter of a rectangle:
P = 2l + 2w
where P is the perimeter, l is the length, and w is the width.
In this case, we have:
P = 2(8) + 2(6) = 28
So the distance of walking along the two sides of the rectangle is 28 miles.
The difference between walking along the two sides and walking diagonally can be found by subtracting the distance of walking along the two sides from the length of the diagonal:
10 - 28 ≈ -18
The absolute value of this difference is 18 miles, so the walk diagonally across the park is approximately 18 miles shorter than walking along the two sides of it.
To know more about rectangle visit:
https://brainly.com/question/29123947
#SPJ1
A college student takes the same number of credits each semester. She had 15 credits when she started, and after 4 semesters, she had 71 credits. Which of these expresses the rate at which she is earning credits?
Answers
Answer:
14 Semesters Per Credit
Step-by-step explanation:

The rate at which she is earning credits is 14 credits per semester.
What is an expression?
Expression in mathematic is defined as the collection of the numbers variables and functions by using signs like addition, subtraction, multiplication, and division.
Here in this question it is given that a college student had 15 credits already when she started her college and at the end of 4 semesters she had 71 credits which means she earned in total 71 - 15 = 56 credits. And the credits she earned is divided equally into all the 4 semesters, Now the rate at which she is earning credits is :
total credits earned by her divided by number of semesters = 56/4 = 14 credits.
Therefore, the rate at which she is earning credits is 14 credits per semester.
Read more about division identity at:
https://brainly.com/question/21416852
#SPJ2
Pls Need this ASAP
When purchasing a home, you need a loan for $80,000. The interest rate of the
loan is 8% and you are required to make monthly payment of $587.

Answers
Answer:
1) 5m
2) 0.25tan
Step-by-step explanation:
(a) Show that if λ is an eigenvalue of A, then λ is an eigenvalue of \(A^{T}\). Show with an example that the eigenvectors of A and \(A^{T}\) are not the same.
(b) Show that if λ is an eigenvalue of A, and A is invertible, then λ^-1 is an eigenvalue of A^-1.
Answers
If λ is an eigenvalue of A, then λ is an eigenvalue of \(A^T\). Show with an example that the eigenvectors of A and \(A^T\) are not the same.
What are eigenvalues and eigenvectors?The equation Av = λv, where v is a non-zero vector, is satisfied by an eigenvector v and an eigenvalue given a square matrix A. In other words, the eigenvector v is multiplied by the matrix A to produce a scalar multiple of v. Due to their role in illuminating the behaviour of linear transformations and differential equation systems, eigenvectors play a crucial role in many branches of mathematics and science. When the eigenvector v is multiplied by A, the eigenvalue indicates how much it is scaled.
The eigenvalue and eigenvector states that, let v be a non-zero eigenvector of A corresponding to the eigenvalue λ.
Then, we have:
Av = λv
Taking transpose on both sides we have:
\(v^T A^T = \lambda v^T\)
The above equations thus relates transpose of vector and transpose of A to λ.
Now, consider a matrix:
\(\left[\begin{array}{cc}1&2\\3&4\\\end{array}\right]\)
Now, the eigen values of this matrix are λ1 = -0.37 and λ2 = 5.37.
The eigenvectors are:
\(v1 = [-0.8246, 0.5658]^T\\v2 = [-0.4159, -0.9094]^T\)
Now, for transpose of A:
\(A^T=\left[\begin{array}{cc}1&3\\2&4\\\end{array}\right]\)
The eigen vectors are:
\(u1 = [-0.7071, -0.7071]^T\\u2 = [0.8944, -0.4472]^T\)
Hence, we see that, if λ is an eigenvalue of A, then λ is an eigenvalue of \(A^T\). Show with an example that the eigenvectors of A and \(A^T\) are not the same.
Learn more about eigenvalues here:
https://brainly.com/question/29749542
#SPJ1
6 veces un numero elevado al cuadrado.
Answers
Answer:
Six squared=36
Step-by-step explanation:
Well, we know squared means 2
So...Think.
Six is not times 2. You might think that, but...
...It's actually multiplying 6 two times
6x6 is 36
You also can think of it as
6x(6 two times)
or 6x(3x2)
Did I answer your question?
Get back to me if I didn't, and I'll help!
Find the equation of the line that is parallel to y=4x+1 and contains the point (1,1)

Answers
SOLUTION
The given equation is:
\(y=4x+1\)Notice that the slope of the given equation is 4.
Recall the slopes of parallel line are equal.
Therefore the slope of the required line is 4.
Since the slope of the required line is 4 and it is given that the line contains the point (1,1)
Then the equation of the line using Point-Slope Form is:
\(\begin{gathered} y-1=4(x-1) \\ y-1=4x-4 \\ y=4x-4+1 \\ y=4x-3 \end{gathered}\)Therefore the required equation is:
\(y=4x-3\)Answer all parts please.

Answers
Answer:
no
Step-by-step explanation:
fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite fortnite
Represent 2x + 3y = 6 by a graph. Write the coordinates of the point where it meets: (a) x-axis
Answers
The point where the line 2x + 3y = 6 intersects the x-axis is (3, 0). This means that when x is equal to 3, y is equal to 0.
To graph the equation 2x + 3y = 6, we can rewrite it in the slope-intercept form, y = mx + b, where m represents the slope and b represents the y-intercept.
Starting with the given equation, we isolate y to one side:
3y = -2x + 6
y = (-2/3)x + 2
Now, we have the equation in slope-intercept form, y = (-2/3)x + 2. The slope is -2/3, and the y-intercept is (0, 2).
To find the point where the graph intersects the x-axis, we need to determine the coordinates where y is equal to zero. This occurs when the line crosses the x-axis.
Setting y = 0 in the equation, we have:
0 = (-2/3)x + 2
(-2/3)x = -2
x = (-2)(-3/2) = 3
Therefore, the point where the line 2x + 3y = 6 intersects the x-axis is (3, 0). This means that when x is equal to 3, y is equal to 0, indicating the point of intersection with the x-axis on the graph.
To more on Graph:
https://brainly.com/question/19040584
#SPJ8
A blueprint for a building includes a rectangular room that measures 3 inches long and 5.5 inches wide. The scale for the blueprint says that 1 inch on the blueprint is equivalent to 10 feet in the actual building. what are the dimensions of this rectangular room in the actual building ?
Answers
Answer:
30 ft long by 55 ft wide
Step-by-step explanation:
What is the time in minutes, taken to cover 8.1
km at an average speed of 5 m/s?
Answers
Answer:
27 minutes
Step-by-step explanation:
(8.1 km)×(1000 m)/(1 km)/(5 m/s)×(1 min/(60 s) = (8.1×1000)/(5×60) min8100/300=27 minwhat is the slope of the line that passes thru (7,-6) and (6,-6)
Answers
The slope of the straight line passing through the two given points is undefined which means the line is parallel to the y-axis.
Let us consider the two points A(x₁,y₁) and B(x₂,y₂) be the two points (7,-6) and (6,-6) on the cartesian coordinates.
Let the slope of the line joining A (7,-6) and B(6,-6) be m.
We know that the slope of a line is given by:
\(m=\frac{y_2-y_1}{x_2-x_1}\)
Slope of the line
= (6-7) / (-6+6)
= -1 / 0
= undefined
Since the slope is undefined we can say that the straight line is parallel to the y axis.
we know that tan 90° = ∞
So any line parallel to this line will have the same slope as the y axis.
Hence the slope of the given line is undefined or infinity.
To learn more about slope visit:
https://brainly.com/question/11559942
#SPJ1
The temperature on Thursday afternoon was 77 °F. A thunderstorm rolled through, and the temperature dropped by 10 °C. What was the temperature after the storm?
Answers
Answer:
15 °C
Step-by-step explanation:
°C = (°F - 32) * (5/9)
Given that the initial temperature was 77 °F and it dropped by 10 °C, we can calculate the final temperature.
Initial temperature: 77 °F
Converting to Celsius:
°C = (77 - 32) * (5/9)
°C ≈ 25
The temperature dropped by 10 °C, so the final temperature is:
Final temperature = Initial temperature - Temperature drop
Final temperature ≈ 25 - 10 = 15 °C
Therefore, the temperature after the storm was approximately 15 °C.
Solve (x+1)2 =13/4 using the square root property
Answers
Answer:
Starting with the equation:
(x + 1)^2 = 13/4
We can use the square root property, which states that if a^2 = b, then a is equal to the positive or negative square root of b.
Taking the square root of both sides, we get:
x + 1 = ±√(13/4)
Simplifying under the radical:
x + 1 = ±(√13)/2
Now we can solve for x by subtracting 1 from both sides:
x = -1 ± (√13)/2
Therefore, the solutions to the equation are:
x = -1 + (√13)/2 or x = -1 - (√13)/2
Step-by-step explanation:
Enter the coordinates of the point
on the unit circle at the given angle.
240°

Answers
EXPLANATION:
To convert degrees to radians, multiply by π / 180 °
since a full circle is 360° or 2π radians.
240°⋅π / 180° radians
Cancel the common factor of 60
4 × π / 3 radians
Combine 4 and π / 3.
4π / 3 radians
HOPE ITS HELPS !!!!!
The coordinates of the points on unit circle at the given angle 240 degrees is\((\frac{-1}{2} ,\frac{-\sqrt{3} }{2} )\)
The formula for calculating Radians is:
\(radians= (degrees)\)×\(\frac{\pi }{180}\)
Formula for calculating coordinates of point (x, y) on circle:x=rcosθ
y=rsinθ (where r is the radius of circle for unit circle r=1)
According to the question
we have
θ = 240 degrees and, r =1
so, 240 degrees = 240×\(\frac{\pi }{180}\)
⇒240 degrees = \(\frac{4\pi }{3}\) (in radians)
Therefore, the coordinates of the points on unit circle at angle \(\frac{4\pi }{3}\) is calculated as
\(x=(1)cos\frac{4\pi }{3}\) (for unit circle r=1)
\(x=\frac{-1}{2}\)
And,
\(y=(1)sin\frac{4\pi }{3}\) (for unit circle r=1)
\(y=\frac{-\sqrt{3} }{2}\)
Hence, the coordinates of the point on unit circle at angle 240 degrees is \((\frac{-1}{2} ,\frac{-\sqrt{3} }{2} )\)
Learn more about coordinates of the point on circle here:
https://brainly.in/question/48723898
#SPJ2
please help if u can! :))))

Answers
Answer: 0.8
Step-by-step explanation:
The formula to find area of a parallelogram is A = bh. This means that area = base x height. You can manipulate this formula to what height equals instead of the area. To do that, you can divide b on both sides. This would make the equation h = A/b.
Now that you know how to find what height equals, first find the base of the parallelogram. To find b, multiply 6 x 5. 6 x 5 = 30. This means that your base is 30.
Take the information given to you in the problem about the area. The area is given to you. We know that the area is 24 squared units. Remember what the equation to find height is. It's h = A/b. Substitute the variables for your numbers. h = 24/30.
24/30 = 0.8.
This means that your height is 0.8. This would be 8/10 in fraction form, but you can simplify it further to 4/5.
Hope it helps. Good luck!
a.) find the test statistic
b.) what is the p-value
c.)what is the conclusion about the null hypothesis
d.) what is the final conclusion?

Answers
a) The test statistic is: t = -1.11.
b) The p-value is: 0.1342.
c) The conclusion is that the null hypothesis is not rejected.
d) The final conclusion is that there is not sufficient evidence to conclude that the population mean is of 6.
What is the test statistic?The standard deviation for the population is unknown, only the sample standard deviation is known, hence the t-distribution is obtain the test statistic.
The test statistic is given by the equation presented as follows:
\(t = \frac{\overline{x} - \mu}{\frac{s}{\sqrt{n}}}\)
In which the variables of the equation are given as follows:
\(\overline{x}\) is the sample mean.\(\mu\) is the value tested at the null hypothesis.s is the standard deviation of the sample.n is the sample size.For this problem, the values of these parameters are as follows:
\(\overline{x} = 5.83, \mu = 6, s = 2.11, n = 189\)
Hence the test statistic is:
\(t = \frac{\overline{x} - \mu}{\frac{s}{\sqrt{n}}}\)
\(t = \frac{5.83 - 6}{\frac{2.11}{\sqrt{189}}}\)
t = -1.11.
P-value and conclusionThe p-value is obtained using a t-distribution calculator, with a left-tailed test, as we are testing if the mean is less a value, with 189 - 1 = 188 df and t = -1.11, hence it is of 0.1342.
Since the p-value is greater than the significance level of 0.10, it is found that:
The null hypothesis is not rejected.There is not sufficient evidence to conclude that the population mean rating is less than 6.More can be learned about the test of an hypothesis at https://brainly.com/question/13873630
#SPJ1
17. Three lines with only two
points of intersection (sketch the figure)
Answers

which the parabola opens,
and determine the y-intercept. Decide which table best illustrates these values for the equation:
y=x² - 6x
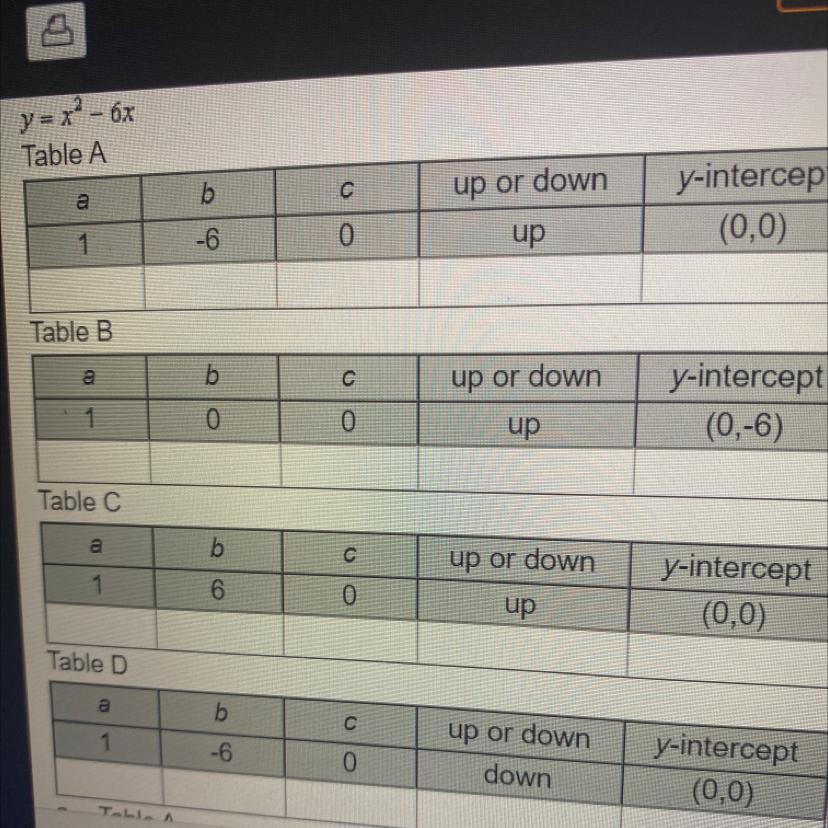
Answers
Table (A) represents the parabola y = x² - 6x in which the parabola opens and the y-intercept is (0, 0) table (A) is the correct choice.
What is a parabola?It is defined as the graph of a quadratic function that has something bowl-shaped.
We have the tables shown in the picture.
We know the quadratic form of a parabola is:
y = ax² + bx + c
If a > 0 the parabola opens
In the equation:
y = x² - 6x
1 > 0 the parabola opens and y-intercept is:
y = 0 (plug x = 0 in the given equation)
a = 1, b = -6, and c = 0
Thus, table (A) represents the parabola y = x² - 6x in which the parabola opens and the y-intercept is (0, 0) table (A) is the correct choice.
Learn more about the parabola here:
brainly.com/question/8708520
#SPJ1

Which of the following is the best array length to reduce the probability of collisions given the set [8, 6, 18, 9, 14, 23]?
a. 8
b. 9
c. 11
d. 12
Answers
The best array length to reduce the probability of collision = 8
Given that,
The best array length to reduce the probability of collisions given the set [8, 6, 18, 9, 14, 23]
What is Collision probability?The collision probability is defined as the probability that the miss distance between two objects is less than the sum of their safety-radii. Each object's positional uncertainties are combined and their radii summed at the point of closest approach.
For i-th element, the probability of total number of collisions = (i-1)/T as there are i-1 previous elements which can collide and T is the total number of possible values.
∑(i=1 to M-1) \(\frac{i}{T}\) = \(\frac{M(M-1)}{2T}\)
Where,
M = number of elements being hashed.
T = total number of hash values in the hash function.
M = number of elements being hashed = [8, 6, 18, 9, 14, 23]
M = 6
T = total number of hash values in the hash function
T = 8 + 6 + 18 + 9 + 14 + 23
T = 78
So,
We can write,
∑(i=1 to M-1) \(\frac{i}{T}\) = \(\frac{M(M-1)}{2T}\)
∑(i=1 to M-1) \(\frac{i}{T}\) = \(\frac{6(6-1)}{78}\)
∑(i=1 to M-1) \(\frac{i}{T}\) = \(\frac{6*5}{78}\)
∑(i=1 to M-1) \(\frac{i}{T}\) = \(\frac{30}{78}\)
∑(i=1 to M-1) \(\frac{i}{T}\) = 0.384
In order to perform a selection sort, we first search the entire given list for the smallest element, swap it with the first element, and then move the smaller element to the end of the sorted list. The second smallest element is then moved to its final position after scanning the list starting with the second element to locate the smallest among the last (n - 1 ) elements.
Since 8 is the smallest element, it will be relocated to index 0 on the first run, and 9—which was in index 0—will take its place.
Therefore,
The best array length to reduce the probability of collision = 8
To learn more about Probability visit :
brainly.com/question/14778979
#SPJ4
What is the percent increase from 40 to 64
Answers
Answer:
60 percent
Step-by-step explanation:
Where: 40 is the old value and 64 is the new value. In this case we have a positive change (increase) of 60 percent because the new value is greater than the old value.
If f(x) = 2x² - 5 and g(x) = 3x + 3, find (f- g)(x).
Answers
Answer:
(f - g)(x) = 2x² - 3x - 8
Step-by-step explanation:
Since , (f - g)(x) = f(x) - g(x)
Then
(f - g)(x) = (2x² - 5) - (3x + 3)
= 2x² - 5 - 3x - 3
= 2x² - 3x - 5 - 3
= 2x² - 3x - 8
Evaluate the expression 10y when y=2.5 .
Answers
Answer:
25
Step-by-step explanation:
Substitute y = 2.5 into the expression
10y = 10 × 2.5 = 25
Bag A has five red marbles and two green ones. Bag & has seven red
marbles and three green ones.
Which bag has the greater probability of drawing a green marble?
Answers
Answer:
bag B
Step-by-step explanation:
bag A: 5R and 2G
bag B: 7R and 3G
Bag A probability for green is 2/7
bag B probability for green is 3/10
if we convert the fractions to have a common denominator:
bag A: 20/70
bag B: 21/70
so bag B has the greater probability of drawing a green marble
The rationale number between -1/3,1/4?
Answers
Answer:
1/6
Step-by-step explanation:
here is it
Figure Y is the result of a transformation on Figure X. Which transformation would accomplish this?
Answers
The interpretation the transformation that creates the graph is 1 unit to the left and 4 units to the right.
Graph: What is it?The link between lines and points is described by a network's mathematical representation, a graph.
Given, that Figure X was transformed to produce Figure Y.
We must ascertain the transformation that is applied in this case.
The process of changing an existing graph or graphed equation to create a different version of the following graph is known as graph transformation. A vertical reflection crosses the x-axis vertically and a horizontal reflection crosses the y-axis horizontally of a graph.
A graph can be horizontally translated by moving the base graph to the left or right in the y-axis direction.
Just a little bit of a tilt to the left and upward is made to the graph.
Figure X undergoes a translation of translation 1 unit left and 4 units up.
Hence translation 1 unit left, and 4 units up is the transformation which accomplish the graph.
To know more about graphs, visit:
https://brainly.com/question/17267403
#SPJ1
The complete question is:
Figure Y is the result of a transformation on Figure X. Which transformation would accomplish this?

Write in standard form
0.000000799
Answers
Answer:
7.99*10^7
is the answer to your question
Answer: 7.99×10\(x^{-7}\)
Step-by-step explanation:
7.99 times 10\(x^{-7}\) = 0.00000799