40 times 30 equals whatttttttt
Answers
Answer:
1200 is your awnser
Step-by-step explanation:
Related Questions
what is the reason these triangles are congruent
a. SSS
B. SAS
C. not congruent

Answers
Answer: SAS
Step-by-step explanation: The angles sides are congruent based on the diagram
I’m having trouble understanding how to solve this someone please help ASAP thank you!
Use the Law of Cosines to solve the problem. You must solve for BC first. Solve this problem in order.
A ship travels due west for 94 miles. It then travels in a northwest direction for 119 miles and ends up 173 miles from its original position. To the nearest tenth of a degree, how many degrees north of west (x) did it
turn when it changed direction? Show your work.

Answers
Answer:
Answer is 71.95°
Step-by-step explanation:
Cosine formula is
a^2=b^2+c^2-2bc(cosA)
cos A =b^2+c^2-a^2/2bc
if a= 119,b=94,c=173
cos A=94^2+173^2-119^2/2(94*173)
=8836+29,929-14,161/2(16,262)
=38765-14,161/32,524
=24604/32,524
=0.7564
cos A=0.7564
cos^-1=40.85°.that's for angle A.
Using the same formula
B=31.1°
C=180-(40.85+31.1)
C=180-71.95
C=108.05
Since angle on a straight line is 180
therefore x is 71.95
Also the sum of angles A and B
help i don’t get it

Answers
Answer:
2.2+3(3.4)
=2.2+10.2
=12.4
Step-by-step explanation:
can someone help me with this?!

Answers
Answer:
x = 4.8
Step-by-step explanation:
6/2 =3
x² = 3² + 3.8²
x² = 9 + 14.44 = 23.44
x = 4.84
heights of 10 year olds, regardless of gender, closely follow a normal distribution with mean 55 inches and standard deviation 6 inches. the height requirement for batman the ride at six flags magic mountain is 54 inches. (a) what percent of 10 year olds cannot go on this ride?
Answers
The percentage of 10-year-olds who cannot go on the ride is approximately 43.32%.
To find the percent of 10 year olds who cannot go on the ride, we need to calculate the area under the normal distribution curve below the height requirement of 54 inches.
First, we need to standardize the height requirement using the formula z = (x - μ) / σ, where x is the height requirement, μ is the mean, and σ is the standard deviation.
Plugging in the values, we get z = (54 - 55) / 6 = -0.17.
Next, we need to find the cumulative probability associated with the z-score of -0.17. We can use a standard normal distribution table or a calculator to find this value.
Using a standard normal distribution table, we find that the cumulative probability associated with a z-score of -0.17 is approximately 0.4332.
This means that approximately 43.32% of 10-year-olds cannot go on this ride, since their height is below the requirement of 54 inches.
The percentage of 10-year-olds who cannot go on the ride is approximately 43.32%.
To know more about cumulative probability, visit:
brainly.com/question/30772963
#SPJ11
a telephone survey of 1000 randomly selected us adults found that 31% of them say they believe in ghosts. does this provide evidence that more than 1 in 4 us adults believe in ghosts? clearly show all details of the test.
Answers
How can a telephone survey of 1000 randomly selected US adults provide evidence that more than 1 in 4 US adults believe in ghosts?The survey results provide evidence that more than one in four US adults believe in ghosts. The telephone survey was conducted on a random sample of 1000 US adults. The survey found that 31 percent of US adults believed in ghosts.
To determine whether more than one in four US adults believe in ghosts, the null and alternative hypotheses will be tested.The null hypothesis in this scenario is that less than or equal to 25% of US adults believe in ghosts. The alternative hypothesis is that more than 25% of US adults believe in ghosts.Therefore, the level of significance (α) will be determined.
The α level is typically set to 0.05. This means that the likelihood of making a type I error is 5%. Then, the z-score will be calculated as follows:z = (0.31 - 0.25) / sqrt[(0.25 x 0.75) / 1000]z = 2.83The obtained z-score will be compared to the critical z-value using a z-distribution table. The critical z-value is 1.96. Since the obtained z-score is greater than the critical z-value, the null hypothesis will be rejected. Therefore, there is evidence to suggest that more than one in four US adults believe in ghosts.
Learn more about telephone survey:
https://brainly.com/question/12992237
#SPJ11
For what amount of exit proceeds would these two structures yield the same amount of carried interest?
.20 (Z-250) = .30 (Z-200)
Solve for Z.
Answers
Answer:
Step-by-step explanation:"To solve this equation, you can start by distributing the 0.20 and 0.30 terms. Then, you can simplify the equation by combining like terms. After that, you can isolate the variable Z on one side of the equation by adding or subtracting terms from both sides. Finally, you can solve for Z. The solution is Z = 1000. Does that help?"
If A and B are mutually exclusive events with P(A) = 0.4 and P(B) = 0.5, then P(A ∩ B) =
a. 0.10
b. 0.90
c. 0.00
d. 0.20
Answers
The probability of A and B occurring simultaneously (P(A ∩ B)) is c. 0.00.
In this scenario, A and B are stated to be mutually exclusive events. Mutually exclusive events are events that cannot occur at the same time. This means that if event A happens, event B cannot happen, and vice versa.
Given that P(A) = 0.4 and P(B) = 0.5, we can deduce that the probability of A occurring is 0.4 and the probability of B occurring is 0.5. Since A and B are mutually exclusive, their intersection (A ∩ B) would be an empty set, meaning no outcomes can be shared between the two events. Therefore, the probability of A and B occurring simultaneously, P(A ∩ B), would be 0.
To further clarify, let's consider an example: Suppose event A represents flipping a coin and getting heads, and event B represents flipping the same coin and getting tails. Since getting heads and getting tails are mutually exclusive outcomes, the intersection of events A and B would be empty. Therefore, the probability of getting both heads and tails in the same coin flip is 0.
In this case, since events A and B are mutually exclusive, the probability of their intersection, P(A ∩ B), is 0.
Therefore, the correct answer is: c. 0.00
Learn more about Probability
brainly.com/question/795909
#SPJ11
At how many points on the curve x 3 + y 3 = 9 in the xy-plane does the curve have a tangent line that is horizontal? None ) One Two Three
Answers
The answer to the question is that there are no points on the curve x3 + y3 = 9 in the xy-plane that have a tangent line that is horizontal.
The equation x3 + y3 = 9 is a cubic equation and is a non-linear equation. As such, it does not have any tangent lines that are horizontal. A tangent line is a line that just touches a point on a curve and has the same slope as the curve at that point. Since the equation is non-linear, the slope of the curve changes at each point, meaning that there cannot be any horizontal tangent lines.
To calculate the slope of the curve at any point (x,y), we use the formula m = (dy/dx) or m = 3*(x2/y2). At these points, the slope of the curve will not be zero, meaning that there is no horizontal tangent line at any point on the curve.
Therefore, the answer to the question is that there are no points on the curve x3 + y3 = 9 in the xy-plane that have a tangent line that is horizontal.
Learn more about tangent lines here:
https://brainly.com/question/23265136
#SPJ4
A stamp has the Length of 1/2 cm and a width of 1 1/2 is the area of the stamps
Answers
Answer:
\(Area = \frac{3}{4} cm^2\)
Step-by-step explanation:
Given
\(Length =\frac{1}{2}\ cm\)
\(Width = 1\frac{1}{2}\ cm\)
Required
Determine the Area
Area is calculated as follows
\(Area = Length * Width\)
Substitute values for Length and Width
\(Area = \frac{1}{2} * 1\frac{1}{2}\)
Convert mixed fraction
\(Area = \frac{1}{2} * \frac{3}{2}\)
\(Area = \frac{3}{4}\)
Hence, the area is
\(Area = \frac{3}{4} cm^2\)
Every morning, Matthew ills his dog’s water dish with 16 oz of water. If his dog finishes his water every day, how many ounces will his dog drink in a week?
How many cups is this?
How many pints is this?
How many quarts is this equal to?
How many quarts is this?
Answers
The dog drinks 112 ounces, or 14 cups, or 7 pints, or 3.5 quarts of water per week.
How to find intake of the dog?The dog drinks 16 oz of water every day, so in a week (7 days), the dog will drink:
16 oz/day × 7 days/week = 112 oz/week
To convert ounces to cups, we divide by 8 (since there are 8 fluid ounces in a cup):
112 oz/week ÷ 8 oz/cup = 14 cups/week
To convert ounces to pints, we divide by 16 (since there are 16 fluid ounces in a pint):
112 oz/week ÷ 16 oz/pint = 7 pints/week
To convert ounces to quarts, we divide by 32 (since there are 32 fluid ounces in a quart):
112 oz/week ÷ 32 oz/quart = 3.5 quarts/week
Therefore, the dog drinks 112 ounces, or 14 cups, or 7 pints, or 3.5 quarts of water per week.
Learn more about ounces
https://brainly.com/question/29374025
#SPJ1
Can u help me with my math

Answers
Answer:
B=310 because..well just do the math.
Step-by-step explanation:
Are the following matrices symmetric, skew-symmetric, or orthogonal? Find the spectrum of each, thereby illustrating and Theorems 1 and 5. Show your work in detail. [1 4 -4 1]
Answers
This matrix is not symmetric, skew-symmetric, or orthogonal and the eigenvalues of the matrix are: λ = (1 + √65) / 2 and λ = (1 - √65) / 2
Symmetric matrices are defined as matrices that are equal to their transpose, meaning that each element in the matrix is equal to the element in the corresponding position of the transpose.
A skew-symmetric matrix is a matrix whose transpose is the negative of itself. Orthogonal matrices are matrices whose inverse is equal to its transpose, meaning that the product of the matrix and its transpose is equal to the identity matrix.
To determine if it is orthogonal, we can check if it satisfies the condition for orthogonality, which is that its transpose is equal to its inverse.
The transpose of the matrix [1 4 -4 1] is:
[1 -4 4 1]
To find the inverse, we need to calculate the determinant of the matrix and the adjugate of the matrix. The determinant is:
(1)(1) - (4)(-4) = 1 + 16 = 17
The adjugate is:
[1 -4 -4 1]
So, the inverse of the matrix is:
[1/17 -4/17 -4/17 1/17]
The transpose of the matrix is not equal to its inverse, so this matrix is not orthogonal.
The spectrum of this matrix can be found by finding its eigenvalues. To do this, we solve for the values of λ that satisfy the characteristic equation:
det (A - λI) = 0
where A is the matrix [1 4 -4 1] and I is the identity matrix.
The determinant of A - λI is:
[1-λ 4 -4 1-λ]
[(1-λ)(1-λ) - (4)(-4) = (1-λ)^2 + 16]
So, we need to find the values of λ that satisfy:
(1-λ)^2 + 16 = 0
This equation can be solved using the quadratic formula:
λ = (-b ± √(b^2 - 4ac)) / 2a
where a = 1, b = -1, and c = -16.
So, λ = (-(-1) ± √((-1)^2 - 4(1)(-16))) / 2(1)
λ = (1 ± √(1 + 64)) / 2
λ = (1 ± √65) / 2
So, the eigenvalues of the matrix are:
λ = (1 + √65) / 2 and λ = (1 - √65) / 2
These are the eigenvalues of the matrix and make up its spectrum.
Learn more about Matrix at:
https://brainly.com/question/28180105
#SPJ4
What do the center and the scale factor need to be in order to transform ACE to triangle ABD?
Answers
A shape must cross a line in order to be reflected.
Because a reflection across BA will map ABC to ABD, the true statement is (c).
What is transformation?A translation only moves a shape up, down, or from side to side; it has no effect on how it appears. An illustration of a transformation is translation. A transformation is a technique for moving or repositioning a shape.
here, we have,
Sides AC and AD of both triangles are congruent
Sides BD and BC of both triangles are congruent
The triangles share a common side AB
This means that a reflection over line AB will map both triangles.
Hence, the true statement is (c)
The complete question is given below.
Is there a rigid transformation that maps triangle ABC to triangle ABD? If so, which transformation?
yes, because a translation to the right will map ΔABC to ΔABD
yes, because a rotation about point B will map ΔABC to ΔABD
yes, because a reflection across BA will map ΔABC to ΔABD
no, because no rigid transformation will map ΔABC to ΔABD
Read more about reflections at:
brainly.com/question/938117
#SPJ1
The test scores for the students in Mr. Miller’s math class are shown here.
52, 61, 69, 76, 82, 84, 85, 90, 94
What is the range of the test scores?
Answers
The range of the test scores in Mr. Miller's math class is 42.
What is the range?Mathematically, the range refers to the difference between the highest value and the lowest value in a data set.
The range is computed by subtraction of the lowest value from the highest value.
Mr. Miller can use the range to measure the spread or dispersion of the test scores.
Test Scores:
52, 61, 69, 76, 82, 84, 85, 90, 94
Highest score = 94
Lowest score = 52
Range = 42 (94 - 52)
Thus, we can conclude that for the math students in Mr. Miller's class, the range of their test scores is 42.
Learn more about the range at https://brainly.com/question/24326172.
#SPJ1
Maria bought g gallons of gasoline for $3.95 per gallon and c cans of oil for $4.45 per can. a. What expression can be used to determine the total amount Maria spent on gasoline and oil? b. If she bought 8.6 gallons of gasoline and 9 cans of oil, how much did she spend in all? a. Choose an expression that represents the amount that Maria spent in all.
Answers
Answer:
a.) Total amount spent on gasoline and oil = $ ( 3.95g + 4.45c )
b.) Total amount spent by Maria = $ 74.02
Step-by-step explanation:
As given,
Cost of gasoline = $ 3.95 gallon
Cost of oil per can = $ 4.45
Also given,
Maria bought g gallons of gasoline and c cans of oil
⇒ Total cost of g gallons of gasoline = g×3.95 = $3.95g
Total cost of c cans of oil = c×4.45 = $4.45c
Now,
a.)
Total amount spent on gasoline and oil = $ ( 3.95g + 4.45c )
b.)
As given ,
Maria buy gasoline , g = 8.6 gallons
Maria buy cans of oil , c = 6
So,
Total amount spent = $ 3.95(8.6) + 4.45(9)
= $ 33.97 + 40.05 = $ 74.02
⇒Total amount spent by Maria = $ 74.02
a random variable x has a mean of 130 and a standard deviation of 15. a random variable y has a mean of 120 and a standard deviation of 9. if x and y are independent, approximately what is the standard deviation of x-y? (a) 24.0 (b) 17.5 (c) 12.0 (d) 6.0 (e) 4.9
Answers
If x and y are independent, then the standard deviation of x-y is 17.5.
The correct option is (b).
If X and Y are independent random variables, the standard deviation of their difference is given by the square root of the sum of their variances.
The standard deviation of x is 15 and the standard deviation of y is 9, we can calculate the variance of x as the square of its standard deviation:
Variance(x) =\((15)^2 = 225\), and the variance of y as \((9)^2 = 81\).
Now, applying the property mentioned earlier, we have:
Standard deviation(x - y) = sqrt(Variance(x) + Variance(y)) = sqrt(225 + 81) = sqrt(306) ≈ 17.49
Rounding the result to one decimal place, we find that the approximate standard deviation of x - y is 17.5.
To know more about standard deviation refer here:
https://brainly.com/question/13498201#
#SPJ11
Find the slope of the line: y+5 = -3/4x
Answers
Answer:
y = -3/4x - 5
Slope: -3/4
y-intercept: -5
HELPPPPP PLEASE. PLEASE TELL ME THE BLANKS IN ORDER.

Answers
so then it would be:
6, 5, 16, 9
The geometric mean and one extreme are given. Find the other extreme.
sqrt24 is the geometric mean between a and b. Find a if b=8/9.
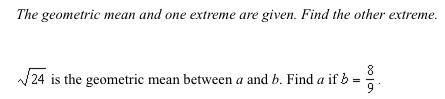
Answers
Answer:
a = 27
Step-by-step explanation:
( √24 )² = \(\frac{8}{9}\) a
a = 24 ÷ \(\frac{8}{9}\) = \(\frac{24}{1}\) × \(\frac{9}{8}\) = 27
a teacher offers gift cards as a reward for classroom participation. the teacher places the gift cards from four different stores into a bag and mixes them well. a student gets to select two gift cards at random (one at a time and without replacement). each outcome in the sample space for the random selection of two gift cards is equally likely. what is the probability of each outcome in the sample space?
Answers
The probability is the same for each outcome since they are equally likely.
Let's assume there are n gift cards in total in the bag. When a student selects two gift cards without replacement, the total number of possible outcomes is the number of ways to choose 2 cards out of n, which can be calculated using the combination formula:
C(n, 2) = n! / (2! * (n - 2)!)
Each of these outcomes has an equal probability of being selected since the gift cards were mixed well, and the selection is random
The probability of each outcome in the sample space can be calculated by dividing 1 by the total number of possible outcomes:
P(outcome) = 1 / C(n, 2).
For example, if there are 4 gift cards in the bag, the total number of possible outcomes is C(4, 2) = 6. Therefore, the probability of each outcome in this case would be 1/6.
In general, the probability of each outcome in the sample space for the random selection of two gift cards is 1 divided by the total number of possible outcomes, ensuring that all outcomes have an equal chance of occurring.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
What is
1. -2(n-9)+4
2. 6x - (2 - 3x)
Answers
Answer:
1) -2n + 22
2) 9x - 2
Step-by-step explanation:
1. -2(n-9)+4
-2n + 18 + 4
-2n + 22
2. 6x - (2-3x)
6x - 2 + 3x
9x - 2
Four students are to solve 5(x-3)=2x+6 which solution and explanation is right?
Answers
Answer: x = 7
Step-by-step explanation: Since I don't know the full question, I only knwo the only to 5(x-3)=2x+6. How you solve it is to isolate the variable by dividing each side by factors that don't contain the variable.
Answer:
x=7
Step-by-step explanation:
distribute 5 to the x and -3
5x-15=2x+6
then you try to get x by itself
I subtracted 2x from 5x and then I got
3x-15=6
then get x by itself still, I added 15 to both sides and I got
3x=21 Then divide and you get
x=7
Hope this helps
If the probability of an event not happening is 24 65 , what is the probability of the event happening
Answers
The probability of the event happening is 41/65, which can be simplified but cannot be further reduced without additional information.
The total probability is universally 1 so the probability of happening is,
Probability of event happening = 1 - Probability of event not happening.
In this case, the probability of event not happening is 24/65. Substituting this value into the formula, we get,
Probability of event happening = 1 - 24/65
To simplify this fraction, we can find a common denominator of 65,
Probability of event happening = (65/65) - (24/65)
This simplifies to,
Probability of event happening = 41/65
Therefore, the probability of the event happening is 41/65.
To know more about probability, visit,
brainly.com/question/13604758
#SPJ4
Suppose you pick people at random and you ask them what month of the year they were born in. Let X be the number of people you have questioned until you find someone born in December. What is E[X], approximately
Answers
Answer:
12
Step-by-step explanation:
I really don't know but I am saying 12 because December is the 12 month of the year.
Let me know if I am correct.
Have an awesome day! :)
A diver is standing on a platform 24 feet above a pool. He jumps from the platform with an initial upward velocity of 8 ft/s. Use the formula h(t) = -16t^2 + 8t + 24, where t is the time in seconds and h is the height in feet. How long will it take for him to hit the water? Show all work.
Answers
The time taken by the diver to hit the water is approximately 1.5 seconds.
To find out how long it will take for the diver to hit the water, we need to determine the value of t when h(t) equals zero.
The given equation is:
h(t) = -16t^2 + 8t + 24
Setting h(t) to zero, we have:
0 = -16t^2 + 8t + 24
To solve this quadratic equation, we can use the quadratic formula:
t = (-b ± √(b^2 - 4ac)) / (2a)
For this equation, a = -16, b = 8, and c = 24.
Substituting these values into the quadratic formula, we get:
t = (-8 ± √(8^2 - 4(-16)(24))) / (2(-16))
Simplifying further:
t = (-8 ± √(64 + 1536)) / (-32)
t = (-8 ± √1600) / (-32)
t = (-8 ± 40) / (-32)
Now we have two possible solutions:
t₁ = (-8 + 40) / (-32)
t₂ = (-8 - 40) / (-32)
Calculating each value separately:
t₁ = 32 / -32
t₁ = -1
t₂ = -48 / -32
t₂ = 1.5
Since time cannot be negative in this context, we discard the negative solution.
It will take the diver approximately 1.5 seconds to hit the water.
For more such questions on time
https://brainly.com/question/26862717
#SPJ8
correct or incorrect? the difference of two numbers is always less than at least one of the numbers
Answers
PLS HELP ME ON THIS QUESTION I WILL MARK YOU AS BRAINLIEST IF YOU KNKW THE ANSWER!!

Answers
Answer: will be D
Step-by-step explanation:
Which of the following graphs does NOT describe y as a function of x?
HELP ASAP!




Answers
Answer:
The second graph is not a function of x
Step-by-step explanation:
Note : -
1st graph : f(x) = secant inverse x
3rd graph : f(x) = c (constant function)
4th graph : It is a function which is +ve
PLEASE I NEED HELP :((((;((((

Answers
Answer:
Complete explanation is in the picture.
Step-by-step explanation:
