4. Triangle RST has the side measures of 8in, 17 in, and 15 in. Is this a righttriangle?I
Answers
If Triangle RST is a right triangle, it satisfies the Pythagorean theorem, which states:
c² = a² + b²
where a and b are the legs, and c is the hypotenuse of the triangle.
Substituting with a = 8, b = 15 and c = 17, we get:
17² = 8² + 15²
289 = 64 + 225
289 = 289
Then, Triangle RST is a right triangle
Related Questions
According to the graph of H(w) below, what happens when w gets very large?
H(W)
(5.0, 20.00)
O A. H(w) equals zero.
O B. H(w) gets very small.
O C. Hw) moves left.
O D. H(w) approaches a vertical asymptote.

Answers
Answer:
B. H(w) gets very small.
Step-by-step explanation:
This should be the answer you're looking for
From the graph of H(w) and w, H(w) gets very small when w gets very large option (B) H(w) gets very small is correct.
What is an exponential function?It is defined as the function that rapidly increases and the value of the exponential function is always positive. It denotes with exponent y = a^x
where a is a constant and a>1
As we know, It is defined as a special type of relationship, and they have a predefined domain and range according to the function every value in the domain is related to exactly one value in the range.
We have a graph shown in the picture.
From the graph:
H(w) represents the vertical axis or y-axis and w represents the horizontal axis or x-axis.
H(w) is decreasing as the w increasing
Thus, from the graph of H(w) and w, H(w) gets very small when w gets very large option (B) H(w) gets very small is correct.
Learn more about the exponential function here:
brainly.com/question/11487261
#SPJ5
What is the square root of -1
Answers
Answer:
i
Step-by-step explanation:
It's imaginary, or it can also be referred to as i.
It took Alfonzo 25 minutes to shop for a shirt. If he left the store at 2:25 P.M. after buying the shirt, what time did he start shopping?
Answers
The time he start shopping is 2 : 00 PM
How to determine the time he start shopping?From the question, we have the following parameters that can be used in our computation:
Time spent = 25 minutes
Time he left the store = 2 : 25PM
Using the above as a guide, we have the following:
Time he started = Time he left the store - Time spent
substitute the known values in the above equation, so, we have the following representation
Time he started = 2 : 25PM - 25 minutes
Evaluate
Time he started = 2 : 00 PM
Hence, the time he start shopping is 2 : 00 PM
Read more about expression at
https://brainly.com/question/15775046
#SPJ1
h(x)=3x−3, find h(3).
Answers
Answer:
hi
Step-by-step explanation:
put 3 in place of x . its like a peice of cake

Answer:
h(3) = 6
Step-by-step explanation:
Given that,
→ x = 3
Then the value of h(3) will be,
→ h(x) = 3x - 3
→ h(3) = 3(3) - 3
→ h(3) = 9 - 3
→ [ h(3) = 6 ]
Hence, the answer is 6.
The tables represent the points earned in each game for a season by two football teams.
Panthers
14 10 10
10 17 3
28 13 17
32 16 10
14 7 21
Cowboys
10 3 8
6 24 12
21 3 10
28 28 7
7 13 3
Which team had the best overall record for the season? Determine the best measure of center to compare and explain your answer.
Panthers; they have a larger median value of 14 points
Cowboys; they have a larger median value of 10 points
Panthers; they have a larger mean value of about 14.8 points
Cowboys; they have a larger mean value of about 12.2 points
Answers
Answer:
Therefore, the Panthers had a better overall record for the season, with a total of 212 points earned compared to the Cowboys' total of 173 points.
Step-by-step explanation:
To compare the measures of center, we can calculate the mean and median points earned by each team:
Panthers: Mean = 212/15 = 14.13 points, Median = 14 points
Cowboys: Mean = 173/15 = 11.53 points, Median = 10 points
Based on these calculations, we can see that the Panthers have a larger mean value of about 14.13 points compared to the Cowboys' mean value of about 11.53 points. However, the median value for both teams is less useful for comparison since they are only one point apart. Therefore, we can conclude that the Panthers had the better overall record for the season based on both the total points earned and their larger mean value.
So, the answer is Panthers; they have a larger mean value of about 14.8 points (Option C is incorrect as the mean value of Panthers is approximately 14.13 and not 14.8).
Find (2,-3) on the coordinate plane.
Step 1 Start at the origin. 2 is the
x-coordinate and it is positive.
So move right 2 units,
Step is the y-coordinate and it is
negative. So move down 3 units.
Find the point on the coordinate plane.
1. (3, 4). Label it A.
2. (-2, 6). Label it B.
3. (5,-5). Label it C
4. (-4,-2). Label it D.
Write the coordinates of the point.
5. E
6. F
7. G.
6. H
Spiral Review
(Chapter 21, Lesson 3) KEY MG 2.1, KEY MG 2.0
9. Plot point (1, 3) on the coordinate grid.
7
10. Plot point (2, 6) on the coordinate grid.
6
5
11. Points (1, 3) and (2, 6) are on the graph of the equation
y = 3x. What are two other points on that graph?
4
3
2
1
0
2
A
4-
3
2
1-
0
70
G
(2-3)
H
1 2 3 4 5 6 7 x

Answers
Answer:
See below.
I really hope it helps! :)
Step-by-step explanation:
(3, 4) location:
(3, 4) is located in quadrant I. From 0, 0, move 3 spaces to the right and 4 spaces up. That will lead you to (3, 4) (point A).(-2, 6) location:
Located in quadrant II. Move 2 spaces to the left (From (0, 0)) and 6 spaces up. (Point B).(5, -5)
(5, -5) is located in quadrant IV. (0, 0), move 5 spaces to the right, then 5 spaces downward. (Point C).(-4, -2)
Located in Quadrant III. From (0, 0), move 4 spaces to the left, then 2 spaces downward.Point E
Located at cords (6, 1).Point F
Located at cords (-4, 3)Point G:
Located at cords (1, -4 or -5)Point H:
Located at cords (2, 5)Sadly, I can't solve the spiral review. I am sorry :(
Help!!!!! find the value of x.

Answers
Answer:
x = 48
Step-by-step explanation:
The two angles shown in the diagram are supplementary and add to 180° because they form a straight line. We can set up an equation:
x - 12 + 3x = 180
4x - 12 = 180
4x = 192
x = 48
Answer:
\(x=42\) ✔︎
Step-by-step explanation:
∠1 + ∠2=1803x+x-12=1804x-12=1804x=180-124x=168x=42°∠1= 3x=3×42=126°
∠2=x-12=42-12= 30°
------------------------------
hope it helps...
have a great day!!
Calculate the actual sales since the sales and sales tax were rung up together. Assume sales tax of 6% and total sales of $33,000.
Answers
Answer:
the actual sales be $31,132
Step-by-step explanation:
The computation of the actual sales is as follows:
Let us suppose the actual sales be x
Now the sales tax be 0.06x
Now the total sales would be
x + 0.06x = $33,000
1.06x = $33,000
x = $33,000 ÷ 1.06
= $31,132
hence, the actual sales be $31,132
The same is to be considered by applying the above equation
Answer:
actual sales be $31,132
Step-by-step explanation:
The ratio 81:108 in the simplest form
Answers
The ratio 81:108 can be simplified to 9:13. To find the simplest form of the ratio, you can divide both numbers by the greatest common factor. The greatest common factor of 81 and 108 is 9, so you can divide both numbers by 9 to get the simplified ratio of 9:13.
In given figure AB is the diameter of circle. If ∠CAD = 32° and ∠CPB = 28°. Find ∠CDA.
Answers
Answer:
Therefore, the angle ∠CDA is 58°.
Step-by-step explanation:
∠CDA = 58°
In the given figure, let's consider the angle ∠CDA as x.
Since AB is the diameter of the circle, we know that the angle subtended by any diameter at any point on the circumference is always 90°. Therefore, ∠CAB = 90°.
In triangle CAD, the sum of angles is 180°. So, we have:
∠CAD + ∠CDA + ∠CAB = 180°
Substituting the known values:
32° + x + 90° = 180°
Combining like terms:
x + 122° = 180°
Subtracting 122° from both sides:
x = 180° - 122°
x = 58°
Solve each system of linear equations below, then check your work.
A. 3x−y=−11 −x+y=5
B -2y+3= 4x + 2 6x + 4y=1
C. 32y- x= -25 5x= 100 + x - 8Y
D. 2y + 3x = 6 4x + 5y +20 = 0
Answers
A. The solution of linear equation is (x, y) = (-3, 8).
B. The solution is (x, y) = (3/4, -1).
C. The solution is (x, y) = (-31/8, 3/8).
D. The solution is (x, y) = (55/7, -117/14).
A. 3x - y = -11 --- (1)
-x + y = 5 --- (2)
From equation (2), we can write y = x + 5, and substitute it in equation (1):
3x - (x + 5) = -11
2x = -6
x = -3
Substituting x in equation (2):
-y = -8
y = 8
Therefore, the solution of the system is (x, y) = (-3, 8).
To check the solution, we substitute the values of x and y in the original equations:
3(-3) - 8 = -11 (True)
-(-3) + 8 = 5 (True)
So, the solution is correct.
B. -2y + 3 = 4x + 2 --- (1)
6x + 4y = 1 --- (2)
From equation (1), we can write 4x + 2 = -2y + 3, and substitute it in equation (2):
6x + 4y = 1
6x - 4y = 8 (rearranging)
12x = 9
x = 3/4
Substituting x in equation (1):
-2y + 3 = 4(3/4) + 2
-2y + 3 = 5
-2y = 2
y = -1
Therefore, the solution of the system is (x, y) = (3/4, -1).
To check the solution, we substitute the values of x and y in the original equations:
-2(-1) + 3 = 4(3/4) + 2 (True)
6(3/4) + 4(-1) = 1 (True)
So, the solution is correct.
C. 32y - x = -25 --- (1)
5x = 100 + x - 8y --- (2)
From equation (2), we can write 4x = 100 - 8y, and substitute it in equation (1):
32y - x = -25
32y - (100 - 8y) = -25
40y = 75
y = 3/8
Substituting y in equation (1):
32(3/8) - x = -25
x = -31/8.
Therefore, the solution of the system is (x, y) = (-31/8, 3/8).
To check the solution, we substitute the values of x and y in the original equations:
32(3/8) - (-31/8) = -25 (True)
5(-31/8) = 100 + (-31/8) - 8(3/8) (True)
So, the solution is correct.
D. To solve the system of equations:
2y + 3x = 6 --- (1)
4x + 5y + 20 = 0 --- (2)
We can rearrange equation (2) to isolate one of the variables:
4x + 5y = -20 (subtracting 20 from both sides)
5y = -4x - 20 (subtracting 4x from both sides)
y = (-4/5)x - 4 (dividing both sides by 5)
Substituting this value of y in equation (1):
2((-4/5)x - 4) + 3x = 6
(-8/5)x - 8 + 3x = 6
(-8/5)x + 3x = 14
(-8/5 + 3)x = 14
(-8/5 + 15/5)x = 14
(7/5)x = 14
x = 10
Substituting this value of x in the equation for y:
y = (-4/5)(10) - 4
y = -12.
Therefore, the solution of the system is (x, y) = (10, -12).
To check the solution, we substitute the values of x and y in the original equations:
2(-12) + 3(10) = 6 (True)
4(10) + 5(-12) + 20 = 0 (True)
So, the solution is correct.
For similar question on linear equations.
https://brainly.com/question/2030026
#SPJ11
work out the following, giving your answer to the simplest form 5 3/5/2 2/3
Answers
Answer:
2 1/10
Step-by-step explanation:
We suppose you want the quotient of the mixed numbers 5 3/5 and 2 2/3.
(5 3/5)/(2 2/3) = (28/5)/(8/3) = (28/5)(3/8) = (4)(7)(3)/(5(4)(2)) = 21/10
= 2 1/10
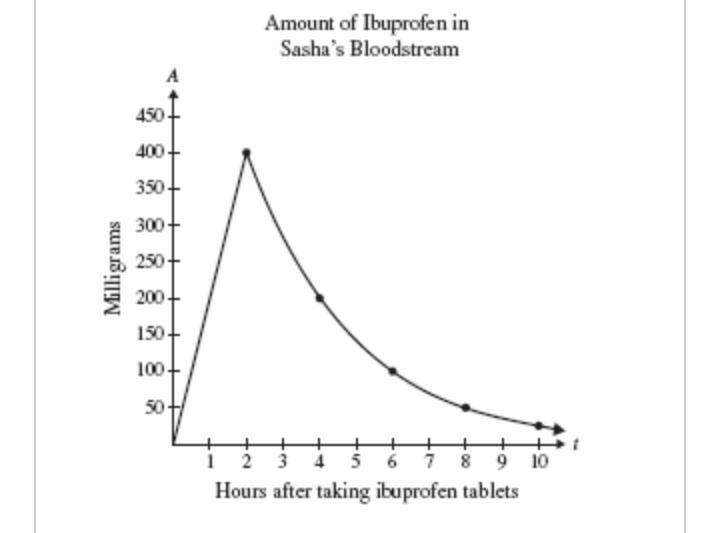
The graph shows the level of ibuprofen, y units, in a patient’s bloodstream x hours after the ibuprofen was taken. Select the correct answer to complete the blanks in the sentence: "The level of ibuprofen in the patient's bloodstream increased from _____ hours to _____ hours."
Answers
The graph is missing, so i have attached it.
Answer:
From 0 hours to 2 hours.
Step-by-step explanation:
From the attached graph, we can see that on the y-axis, denotes the level of ibuprofen in the patient’s bloodstream while the x-axis denotes the amount of hours after the ibuprofen was taken.
Now, looking at the graph, we can see that the curve goes up from a time of 0 hours which corresponds to 0 mg of ibuprofen to a time of 2 hours which corresponds to 400 mg of ibuprofen.
After that point, the curve begins to to go down. Since we are concerned with increase, we will make do with the first statement.
Thus, we can say the period at which the level of ibuprofen increased was from 0 hours to 2 hours.
Suppose that ƒ is a function given as f(x) = 4x² + 5x + 3.
Simplify the expression f(x + h).
f(x + h)
Simplify the difference quotient,
ƒ(x + h) − ƒ(x)
h
=
Submit Question
The derivative of the function at x is the limit of the difference quotient as h approaches zero.
f(x+h)-f(x)
f'(x) =lim
h→0
h
ƒ(x + h) − f(x)
h
=

Answers
Answer:
f(x +h) = 4x² +4h² +8xh +5x +5h +3
(f(x+h) -f(x))/h = 4h +8x +5
f'(x) = 8x +5
Step-by-step explanation:
For f(x) = 4x² +5x +3, you want the simplified expression f(x+h), the difference quotient (f(x+h) -f(x))/h, and the value of that at h=0.
F(x+h)Put (x+h) where h is in the function, and simplify:
f(x+h) = 4(x+h)² +5(x+h) +3
= 4(x² +2xh +h²) +5x +5h +3
f(x +h) = 4x² +4h² +8xh +5x +5h +3
Difference quotientThe difference quotient is ...
(f(x+h) -f(x))/h = ((4x² +4h² +8xh +5x +5h +3) - (4x² +5x +3))/h
= (4h² +8xh +5h)/h
(f(x+h) -f(x))/h = 4h +8x +5
LimitWhen h=0, the value of this is ...
f'(x) = 4·0 +8x +5
f'(x) = 8x +5
__
Additional comment
Technically, the difference quotient is undefined at h=0, because h is in the denominator, and we cannot divide by 0. The limit as h→0 will be the value of the simplified rational expression that has h canceled from every term of the difference. This will always be the case for difference quotients for polynomial functions.
<95141404393>

Lisa has $7.80 to spend on some tomatoes and a loaf of bread tomatoes cost 1.20 a pound and a loaf of bread cost 1.80 the inequality is 1.20x+1.80< 7.80 _solve the inequality. how many pounds of Tomatoes can Lisa Buy
Answers
An arrow is shot from 3 ft above the top of a hill with a vertical upward velocity of 108 ft/s. If it strikes the plain below after 9.5 s, how high is the hill?
If the arrow is launched at t0, then write an equation describing velocity as a function of time?
Answers
The height of the hill is approximately 25.73 ft. Where v0 is the initial velocity (108 ft/s), g is the acceleration due to gravity \((-32.2 ft/s^2)\),
To find the height of the hill, we can use the formula for the vertical position of an object under constant acceleration:
h = h0 + v0t + 1/2at^2
where h is the final height, h0 is the initial height, v0 is the initial velocity, t is the time, and a is the acceleration due to gravity (-32.2 ft/s^2).
In this case, we are given that the initial height h0 is 3 ft, the initial velocity v0 is 108 ft/s, and the time t is 9.5 s. We want to find the height of the hill, which we can denote as h_hill. The final height is the height of the plain, which we can denote as h_plain and assume is zero.
At the highest point of its trajectory, the arrow will have zero vertical velocity, since it will have stopped rising and just started to fall. So we can set the velocity to zero and solve for the time it takes for that to occur. Using the formula for velocity under constant acceleration:
v = v0 + at
we can solve for t when v = 0, h0 = 3 ft, v0 = 108 ft/s, and a = -32.2 ft/s^2:
0 = 108 - 32.2t
t = 108/32.2 ≈ 3.35 s
Thus, it takes the arrow approximately 3.35 s to reach the top of its trajectory.
Using the formula for the height of an object at a given time, we can find the height of the hill by subtracting the height of the arrow at the top of its trajectory from the initial height:
h_hill = h0 + v0t + 1/2at^2 - h_top
where h_top is the height of the arrow at the top of its trajectory. We can find h_top using the formula for the height of an object at the maximum height of its trajectory:
h_top = h0 + v0^2/2a
Plugging in the given values, we get:
h_top = 3 + (108^2)/(2*(-32.2)) ≈ 196.78 ft
Plugging this into the first equation, we get:
h_hill = 3 + 108(3.35) + 1/2(-32.2)(3.35)^2 - 196.78
h_hill ≈ 25.73 ft
If the arrow is launched at t0, the equation describing velocity as a function of time would be:
v(t) = v0 - gt
For such more questions on velocity
https://brainly.com/question/25749514
#SPJ8
What is 32 divided by the opposite of 4
Answers
Answer: -8
Since we are dividing the OPPOSITE of 4 then we are dividing 32÷-4
When multiplying or dividing a POSITIVE to a NEGATIVE you get a NEGATIVE
P/N=N
N/N=P
P*P=P
P=Positive
N=Negative
Divide
32/-4=-8
So your answer is -8
When 32 is divided by opposite of 4 the obtained result is - 8.
What is additive inverse ?Additive inverse of a number is such a number when the original number and it's additive inverse is added we get zero.
4 + ( - 4 ) = 0.So the additive inverse of 4 is - 4.
According to the given question we have to obtain the result when 32 is divided by opposite of 4.
Here opposite of 4 means additive inverse of 4 which is -4.
∴ 32/-4
= - 8.
learn more about additive inverse here :
https://brainly.com/question/13715269
#SPJ2
Solve the problem. The surface area of a square pyramid is 116 in.2 and the total area of the pyramid’s four triangular faces is 80 in.2 What is the length of one of the sides?
Answers
The length of one of the sides of the square base is 6 inches.
Length calculation.
Let's denote the length of one of the sides of the square base by "s" and the height of the pyramid by "h". Then, the surface area of the pyramid can be expressed as:
Surface area = area of square base + sum of areas of four triangular faces
Surface area = s^2 + 4(1/2)(s)(h)
We know that the surface area is 116 in^2 and the sum of the areas of the four triangular faces is 80 in^2. So we can substitute these values into the equation:
116 = s^2 + 4(1/2)(s)(h)
80 = 4(1/2)(s)(h)
We can simplify the second equation to get:
20 = (1/2)(s)(h)
We can solve for h by substituting the value of (1/2)(s)(h) from the second equation into the first equation:
116 = s^2 + 4(20)
116 = s^2 + 80
s^2 = 36
s = 6
Therefore, the length of one of the sides of the square base is 6 inches.
Learn more about length below.
https://brainly.com/question/28322552
#SPJ1
Which expression is equivalent to StartRoot 8 x Superscript 7 Baseline y Superscript 8 Baseline EndRoot? Assume x greater-than-or-equal-to 0.
x y squared StartRoot 8 x cubed EndRoot
2 x cubed y cubed StartRoot x y squared EndRoot
2 x cubed y Superscript 4 Baseline StartRoot 2 x EndRoot
4 x cubed y Superscript 4 Baseline StartRoot x EndRoot
Answers
The expression that is equivalent to StartRoot \(8 x^7 y^8\) EndRoot is (\(2 x^3 y^4\) StartRoot 2 x EndRoot)^2.
To understand why this is the case, let's break down each expression and simplify them step by step:
StartRoot \(8 x^7 y^8\) EndRoot:
We can rewrite 8 as \(2^3\), and since the square root can be split over multiplication, we have StartRoot \((2^3) x^7 y^8\) EndRoot. Applying the exponent rule for square roots, we get StartRoot \(2^3\) EndRoot StartRoot \(x^7\) EndRoot StartRoot \(y^8\) EndRoot.
Simplifying further, we have 2 StartRoot \(2 x^3 y^4\) EndRoot StartRoot \(2^2\) EndRoot StartRoot \(x^2\) EndRoot StartRoot \(y^4\) EndRoot. Finally, we obtain 2 \(x^3 y^4\) StartRoot 2 x EndRoot, which is the expression in question.
(\(2 x y^2\) StartRoot 8 x^3 EndRoot)^2:
Expanding the expression inside the parentheses, we have \(2 x y^2\)StartRoot \((2^3) x^3\) EndRoot. Applying the exponent rule for square roots, we get \(2 x y^2\) StartRoot \(2^3\) EndRoot StartRoot \(x^3\) EndRoot.
Simplifying further, we have \(2 x y^2\) StartRoot 2 x EndRoot. Squaring the entire expression, we obtain (\(2 x y^2\) StartRoot 2 x EndRoot)^2.
Therefore, the expression (\(2 x^3 y^4\) StartRoot 2 x EndRoot)^2 is equivalent to StartRoot \(8 x^7 y^8\) EndRoot.
For more such questions on expression
https://brainly.com/question/1859113
#SPJ8
Please help me, no links or random answers, please. When you are writing the answer please number it so I know which answer is for which question.

Answers
Answer:
Step-by-step explanation:
a. Y intercept is where the line crosses the y axis, so for l1 it’s (0,4). Answer is 4.
b. Y intercept for l2 is point (0,2). Answer is 2.
c. l1 gradient is -1/2. Rise/run
So l1 equation is y = -1/2x + 4
l2 gradient is 1.
Equation is y = x + 2
e. x+2= -1/2x + 4
1.5x = 2
x = 1.333...
y = plug into one of the equations value of x. So y = 3.333...
f. 1.33+ 2 = 3.33
-1/2 times 1.33 + 4 = 3.33 (rounded)
PLEASE HELP ME ITS ALGEBRA THANK YOUUUU

Answers
IM WRONG NVM ..........
Two similar octagons have areas of 4 ft2 and 16 ft2. Find their similarity ratio.
1:4
1:2
1:16
1:8
Answers
The similarity ratio between the two octagons is 1:2 (Option b).
To begin, we need to know that similar figures have the same shape, but they may differ in size. For instance, we can have two octagons with different areas but the same shape. In this case, we are given that the two octagons are similar, and we are given the areas of the two octagons.
Let the similarity ratio between the two octagons be "x". For areas, we know that the ratio of the areas of two similar figures is the square of their similarity ratio. Therefore, we can set up the following equation:
x² = (Area of smaller octagon) / (Area of larger octagon)
Substituting the given areas, we get:
x² = 4 / 16
x² = 0.25
Taking the square root of both sides, we get:
x = √0.25
x = 0.5
Therefore, the similarity ratio between the two octagons is 1:2 (Option b).
To know more about similarity ratio here
https://brainly.com/question/822659
#SPJ1
Look for factors that will help you determine what type of economy exists in Country A.
Based on the clues in this passage, what type of economy does Country A have?
developed
developing
transitioning
command
Answers
developing:
a low GDP
an economy based on agriculture
Based on the limited information provided, it is not possible to definitively determine the type of economy in Country A. More specific details and factors would be necessary to make a conclusive determination.
The product of two consecutive integers is 420. Which quadratic equation can be used to find x, the lesser number?
O x2 + 1 = 420
O x2 + 2 = 420
O x2 + x = 420
O x2 + 2x = 420
Need help asap
Answers
Answer:
0 x2+2=420
Step-by-step explanation:
The quadratic equation can be used to find x is x²+x=420
What is quadratic equations?
A quadratic equation is a second order polynomial of the form ax²+bx+c=0, where a≠0. The root of the quadratic equation can be found by formula x={-b±√(b²-4ac)}/2a.
Let the two consecutive integers are x and x+1.
Then according to question,
x(x+1)=420
x²+x=420
Hence the quadratic equation can be used to find x is x²+x=420
To learn more about quadratic equations click here:
https://brainly.com/question/17660277
#SPJ7
Ten posts were used to secure the fence. A hole was dug for each post and a total of 23.5 pounds of concrete were poured into the holes. An equal amount of concrete was poured into each hole. How much concrete was poured into each hole?
Answers
The amount of concrete poured into each hole is given by A = 2.35 pounds
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be represented as A
Now , the value of A is
Substituting the values in the equation , we get
Let the amount of concrete poured into each hole be A
Now , the total amount of concrete = 23.5 pounds
Ten posts were used to secure the fence. A hole was dug for each post.
So , the total number of holes = 10 holes
Now , the amount of concrete poured into 10 holes = total amount of concrete / 10
On simplifying the equation , we get
The amount of concrete poured into each hole is A = 23.5 / 10
The amount of concrete poured into each hole is A = 2.35 pounds
Hence , the equation is A = 2.35 pounds
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
Justin runs each lap in 8 minutes. He will run at most 10 laps today. What are the possible numbers of minutes he will run today?
Answers
Which of the following could be an equation of g?

Answers
A) g(x)= (x-5)(x-9)
This is the answer because basically you need to find the roots of the function, since the function g intersects the x-axis at x=5 and x=9 you can conclude easily that those are the roots.
If:
x=5
g(5)=(5-5)(5-9)=0(-4)=0
and
If:
x=9
g(9)=(9-5)(9-9)=(4)(0)=0
Weights of Minivans The average weight of 40 ran- domly selected minivans was 4150 pounds. The popula- tion standard deviation was 480 pounds. Find a point es- timate of the population mean. Find the 99% confidence interval of the true mean weight of the minivans.
Answers
Answer:
99% confidence interval of the true mean weight of the minivans
(3954.192 ,4345.808)
Step-by-step explanation:
step(i):-
Given sample size 'n' = 40
mean of the sample x⁻ = 4150 pounds
Standard deviation of the Population 'σ' = 480 pounds
Critical value:-
\(Z_{\frac{\alpha }{2} } = Z_{\frac{0.01}{2} } = Z_{0.005} = 2.58\)
step(ii):-
99% confidence interval of the true mean weight of the minivans
\((x^{-} - Z_{\frac{\alpha }{2} } \frac{S.D}{\sqrt{n} } , x^{-} - Z_{\frac{\alpha }{2} } \frac{S.D}{\sqrt{n} })\)
\((4150 - 2.58 \frac{480}{\sqrt{40} } , 4150 - 2.58 \frac{480}{\sqrt{40} })\)
(4150 - 195.808 , 4150 + 195.808)
(3954.192 ,4345.808)
Conclusion:-
99% confidence interval of the true mean weight of the minivans
(3954.192 ,4345.808)
please answer thank you

Answers
Answer:
Option A
Step-by-step explanation:
Given function is,
f(x) = x² + 3x + 5
We have to find the value of f(a + h) so we will substitute (a + h) in place of x, and simplify the expression.
f(a + h) = (a + h)² + 3(a + h) + 5
= a² + 2ah + h² + 3(a + h) + 5 [(a + b)² = a² + 2ab + b²]
= a² + 2ah + h² + 3a + 3h + 5
Therefore, Option A will be the answer.
The price-demand and cost functions for the production of microwaves are given asP= 180 - q/50and C(q) = 72000 + 110g,where q is the number of microwaves that can be sold at a price of p dollars per unit and C(q) is the total cost (in dollars) of producing q units.(C) Find the marginal revenue function in terms of q.R'(q) =(D) Evaluate the marginal revenue function at q=1100.R'(1100) =(E) Find the profit function in terms of q.P(q)(F) Evaluate the marginal proft function at q = 1100.P'(1100)

Answers
Answer:
A)
\(\begin{equation*} C^{\prime}(q)=110 \end{equation*}\)B)
\(\begin{equation*} R(q)=180q-\frac{q^2}{50} \end{equation*}\)C)
\(\begin{equation*} R^{\prime}(q)=180-\frac{q}{25} \end{equation*}\)D)
\(\begin{equation*} R^{\prime}(1100)=136 \end{equation*}\)E)
\(\begin{equation*} P(q)=-\frac{q^2}{50}+70q-72000 \end{equation*}\)F)
\(\begin{equation*} P^{\prime}(1100)=26 \end{equation*}\)Explanation:
Given:
\(\begin{gathered} p=180-\frac{q}{50} \\ C(q)=72000+110q \end{gathered}\)where q = the number of microwaves that can be sold at a price of p dollars per unit
C(q) = the total cost (in dollars) of producing q units.
A) To find the marginal cost, C'(q), we'll go ahead and take the derivative of the total cost as seen below;
\(\begin{gathered} C(q)=72000+110q \\ C^{\prime}(q)=0+110 \\ \therefore C^{\prime}(q)=110 \end{gathered}\)So the marginal cost, C'(q) = 110
B) We'll go ahead and determine the revenue function, R(q), by multiplying the price, p, by the quantity, q, as seen below;
\(\begin{gathered} R(q)=p*q=(180-\frac{q}{50})q=180q-\frac{q^2}{50} \\ \therefore R(q)=180q-\frac{q^2}{50} \end{gathered}\)C) We'll go ahead and determine the marginal revenue function, R'(q), by taking the derivative of the revenue function, R(q);
\(\begin{gathered} \begin{equation*} R(q)=180q-\frac{q^2}{50} \end{equation*} \\ R^{\prime}(q)=180-\frac{2q^{2-1}}{50}=180-\frac{q}{25} \\ \therefore R^{\prime}(q)=180-\frac{q}{25} \end{gathered}\)D) To evaluate the marginal revenue function at q = 1100, all we need to do is substitute the q with 1100 in R'(q) and simplify;
\(\begin{gathered} \begin{equation*} R^{\prime}(q)=180-\frac{q}{25} \end{equation*} \\ R^{\prime}(1100)=180-\frac{1100}{25}=180-44=136 \\ \therefore R^{\prime}(1100)=136 \end{gathered}\)Therefore, R'(1100) is 136
E) To find the profit function, P(q), we have to subtract the total cost, C(q), from the revenue cost, R(q);
\(\begin{gathered} P(q)=R(q)-C(q) \\ =(180q-\frac{q^2}{50})-(72,000+110q) \\ =180q-\frac{q^2}{50}-72000-110q \\ =-\frac{q^2}{50}+180q-110q-72000 \\ =-\frac{q^2}{50}+70q-72000 \\ \therefore P(q)=-\frac{q^2}{50}+70q-72000 \end{gathered}\)F) To Evaluate the marginal profit function at q = 1100, we have to first determine the marginal profit, P'(q), by taking the derivative of the profit function, P(x);
\(\begin{gathered} \begin{equation*} P(q)=-\frac{q^2}{50}+70q-72000 \end{equation*} \\ P^{\prime}(q)=-\frac{2q^{2-1}}{50}+70(1*q^{1-1})-0=-2q^{50}+70q^0=-\frac{q}{25}+70 \\ \therefore P^{\prime}(q)=-\frac{q}{25}+70 \end{gathered}\)We can now go ahead and find P'(1100) as seen below;
\(\begin{gathered} P^{\prime}(1100)=-\frac{1100}{25}+70=-44+70=26 \\ \therefore P^{\prime}(1100)=26 \end{gathered}\)So P'(1100) = 26