4. The distribution of the heights of students in a large class is roughly Normal. The average height is 68inches, and approximately 99.7% of the heights are between 62 and 74 inches. Thus, the variance of theheight distribution is approximately equal to(A) 2(B) 3(C) 4D 6(E) 9
Answers
Step 1: Let's recall the 68 - 95 - 99.7 rule for a standard normal distribution, as follows:
• 68% of data falls within the first standard deviation from the mean
,• 95% of data falls within the second standard deviation from the mean
,• And, finally 99.7% of data falls within the third standard deviation from the mean
Step 2: Now, let's calculate the value of the standard deviation for the heights of students in this large class, this way:
3 * Standard deviation = Upper limit - Mean
Replacing with the values given in the exercise, we have:
3 * Standard deviation = 74 - 68
3 * Standard deviation = 6
Dividing by 3 at both sides:
3 * Standard deviation/3 = 6/3
Standard deviation = 2 inches
Step 3: Let's also recall that the standard deviation of a sample or of a population is equal to the square root of the variance. Then, using that formula, let's find the variance for this normal distribution.
Standard deviation = √Variance
2 = √Variance
Squaring to both sides:
\(2^2\text{ = (}\sqrt{Variance})^2\)Variance = 4 square inches
The correct answer is C. 4
Related Questions
Consider a circle whose equation is x2 + y2 – 2x – 8 = 0. Which statements are true? Select three options.
The radius of the circle is 3 units.
The center of the circle lies on the x-axis.
The center of the circle lies on the y-axis.
The standard form of the equation is (x – 1)² + y² = 3.
The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.
Answers
The three statements that are true include the following:
A. The radius of the circle is 3 units.
B. The center of the circle lies on the x-axis.
D. The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.
What is the equation of a circle?In Mathematics, the standard form of the equation of a circle is represented by this mathematical expression;
(x - h)² + (y - k)² = r² .......equation 1.
Where:
h and k represents the coordinates at the center of a circle.
r represents the radius of a circle.
Based on the information provided, we have the following equation of a circle:
x² + y² – 2x – 8 = 0 ......equation 2.
In order to determine the true statements, we would rewrite the equation in standard form and then factorize by using completing the square method:
x² – 2x + y² = 8 = 0
x² – 2x + (2/2)² + y² = 8 + (2/2)²
x² – 2x + 1 + y² = 8 + 1
(x – 1)² + (y - 0)² = 9 .......equation 3.
By comparing equation 1 and equation 3, we have the following:
Center (h, k) = (1, 0)
Radius (r) = 3
Additionally, this line and the center of the given circle lies on the x-axis (x-coordinate) because the y-value is equal to zero (0).
(x - 0)² + (y - 0)² = 3²
x² + y² = 9.
Read more on equation of a circle here: brainly.com/question/17028215
#SPJ1
math project : I need an interesting project idea for mathematics that can relate 3 different topics, I should write a full research paper related on the topic this are some examples related to the project
You must state a question that you would like to answer. This must be a specific question within your topic and should be explored thoroughly to create a complete paper.
Examples:
(i) How can we use Mathematical/Calculus-based tools to study the spread of COVID-19?
(ii) Designing a new Mathematical/Calculus-based model to analyze the spread of COVID-19
(iii) How many entrances should there be at Expo to accommodate all visitors?
(iv) How much water does the UAE need in order to sustain its ever changing population? (i.e. comparing water usage vs. water production)
Literature review:
You must show using multiple references and sources of the current literature on your given topic. This does NOT imply that information is simply copied from the internet but rather you must present a comprehensive review and summary of the latest research on your topic. It is suggested that you chose a specific aspect of your topic in order to include all required elements.
Examples:
(i) Review of the existing Mathematical/Calculus-based models used to analyze the spread of COVID-19
(ii) Review of existing Mathematical/Calculus-based models and calculations regarding risk insurance.
Answers
Answer:
Here's an interesting project idea for mathematics that can relate three different topics:
Topic 1: Fractals
Topic 2: Chaos Theory
Topic 3: Differential Equations
Research Question: Can fractals be used to model chaotic systems described by differential equations?
In this project, you can explore the concept of fractals and their applications in modeling complex systems. You can also delve into chaos theory and differential equations to understand how they are used to describe chaotic systems. By combining these three topics, you can investigate whether fractals can provide a better understanding of chaotic systems by modeling them more accurately.
Your research paper can cover the following areas:
Introduction: Provide an overview of fractals, chaos theory, and differential equations, and explain their relevance to the research question.
Fractals: Discuss the properties of fractals and how they can be used to model complex systems. Provide examples of fractals in nature and technology.
Chaos Theory: Explain the concept of chaos and how it is described by differential equations. Discuss the importance of chaos theory in understanding complex systems.
Differential Equations: Provide an overview of differential equations and their applications in physics, engineering, and other fields. Explain how differential equations are used to model chaotic systems.
Combining the three topics: Explain how fractals can be used to model chaotic systems described by differential equations. Provide examples of fractals used in modeling chaotic systems and compare the results to traditional methods.
Conclusion: Summarize the findings of your research and discuss the implications of using fractals to model chaotic systems.
Overall, this project can be a challenging and rewarding exploration of the interplay between three different mathematical topics.
Step-by-step explanation:
Simplify the polynomial, then evaluate for x = 2.
x+3x²+2x-3-4x²+6
x² + 3x + 9; 19
x² + 3x + 3; 5
-x² + 3x + 9; 11
O
O
-x² + 3x + 3; 13
Answers
Answer:
x^2 + 3x + 9 = (x + 3)(x + 3)
When x = 2, we have:
(2 + 3) * (2 + 3)
5 * 5
25
Agilemind assignment test

Answers
Answer:
3.43°
Step-by-step explanation:
tan(angle of inclination of the highway)=6/100
angle=tan^-1(6/100)
angle=3.43°
If the Midpoint Rule is used on the interval [,] with n subintervals, at what x-coordinates is the integrand evaluated?
Answers
The x-coordinates at which the integrand is evaluated when using the Midpoint Rule on the interval [a, b] with n subintervals are the midpoints of each subinterval, given by the formulas xᵢ = a + (step size) / 2 + (i - 1) * (step size) for i = 1 to n.
When using the Midpoint Rule to approximate the value of an integral on the interval [a, b] with n subintervals, the x-coordinates at which the integrand is evaluated are the midpoints of each subinterval.
To divide the interval into n subintervals, we use a step size of (b - a) / n. Then, the x-coordinates of the midpoints can be calculated as follows:
First subinterval:
x₁ = a + (step size) / 2
Second subinterval:
x₂ = a + (step size) / 2 + (step size)
Third subinterval:
x₃ = a + (step size) / 2 + 2 * (step size)
And so on, up to the nth subinterval:
xₙ = a + (step size) / 2 + (n - 1) * (step size)
for such more question on coordinates
https://brainly.com/question/30107320
#SPJ8
The x-coordinates at which the integrand is evaluated using the Midpoint Rule on the interval [-1, 23] with n subintervals can be represented by the formula \(x_i = -1 + (24i - 12) / (2n)\).
To determine the x-coordinates at which the integrand is evaluated using the Midpoint Rule on the interval [-1, 23] with n subintervals, we can follow these steps:
Calculate the width of each subinterval, Δx, by dividing the length of the interval [a, b] by the number of subintervals, n:
Δx = (b - a) / n
In this case, a = -1 and b = 23.
Substitute the values of a, b, and n;
Δx = (23 - (-1)) / n
Δx = 24 / n
Determine the x-coordinate of the midpoint for each subinterval using the formula:
\(x_i\) = a + (i - 1/2) Δx
where i ranges from 1 to n.
\(x_i\) = -1 + (i - 1/2) (24 / n)
\(x_i\) = -1 + (24i - 12) / (2n)
Learn more about Midpoint Rule here:
brainly.com/question/17218343
#SPJ4
500.00
-319.45 = m
Solve for m
Answers
Answer:
STo solve for m in the equation -319.45 = m, we can isolate the variable m by adding 319.45 to both sides of the equation:
-319.45 + 319.45 = m + 319.45
This simplifies to:
0 = m + 319.45
Finally, we can subtract 319.45 from both sides to solve for m:
0 - 319.45 = m + 319.45 - 319.45
-319.45 = m
Therefore, the value of m is -319.45.tep-by-step explanation:
3. A trail mix recipe asks for 4 cups of raisins for every 6 cups of peanuts
There is a proportional relationship between the amount of raisins (cups) and the amount of peanuts p (cups), in this recipe
a. Write the equation for the relationship that has constant of
proportionality greater than 1 Graph the relationship
b. Write the equation for the relationship that has a constant of
proportionality less than 1. Graph the relationship

Answers
Level: Grade 7 Mathematics
----
Steps & Solution:
1. The relationship that has constant of proportionality greater than 1
\(\frac{p}{r} =\frac{6}{4} =\frac{3}{2}\) { the calculator of a certain proportionaility }
\(p=\frac{3}{2} r\)
2. The relationship that has constant of proportionaility less than 1
\(\frac{r}{p} =\frac{4}{6} =\frac{2}{3} \\r=\frac{2}{3} p\)
What is the simplest form of the radical expression?
√2 + √3 / √2 - √3
Answers
The simplest form of the radical expression (√2 + √3) / (√2 - √3) is -5 - 2√6.
What is the simplest form of the given radical expression?Given the radical expression in the question;
(√2 + √3) / (√2 - √3)
To simplify the expression, we need to eliminate the radical in the denominator.
We can do this by multiplying both the numerator and denominator by the conjugate of the denominator, which is (√2 + √3):
[(√2 + √3) / (√2 - √3)] × [ (√2 + √3) / (√2 + √3) ]
= (2 + √6 + √6 + 3) / (2 - √9)
= (5 + 2√6) / (2 - 3)
= (5 + 2√6) / (-1)
= -5 - 2√6
Therefore, the simplified form is -5 - 2√6.
Learn more about surds at: brainly.com/question/840021
#SPJ1
A B and C are points on the circle find obtuse angle aoc

Answers
The value of the obtuse angle AOC is 100°.
What is an obtuse angle?
Obtuse angle is any angle greater than 90° but less than 180°.
To calculate the value of the obtuse angle AOC, use the formula below
Formula:
Obtuse ∠AOC = 360-Reflex ∠AOC.................. Equation 1 ( Sum of the angle at a point)But,
Reflex ∠AOC = 2×∠ABC..................... Equation 2 (The angle substend by an arc at the center of the circle)From the diagram,
Given:
∠ABC = 130°Substitute the value into equation 2
Reflex ∠AOC = 2×130 = 260°Therefore,
Obtuse ∠AOC = (360-260)Obtuse ∠AOC = 100°Learn more about obtuse angle here: https://brainly.com/question/3250447
#SPJ1
x-intercept of 3 and y-intercept of 8
How do you write a lunar equation given this information and how do you write the equation in slope form
Answers
Answer:
y = -8/3x + 8
Step-by-step explanation:
Step 1: Identify which values we have and need to find in the slope-intercept form:
The general equation of the slope-intercept form of a line is given by:
y = mx + b, where
(x, y) is any point,m is the slope,and b is the y-intercept.Since we're told that the y-intercept is 8, this is our b value in the slope-intercept form.
Step 2: Find m, the slope of the line:
Since the x-intercept is 3, the entire coordinates of the x-intercept are (3, 0)Thus, we can find m, the slope of the line by plugging in (3, 0) for (x, y) and 8 for b:
0 = m(3) + 8
0 = 3m + 8
-8 = 3m
-8/3 = m
Thus, the slope is -8/3.
Therefore, the the equation of the line in slope-intercept form whose x-intercept is 3 and whose y-intercept is 8 is y = -8/3x + 8.
Optional Step 3: Check the validity of the answer:
We know that the entire coordinates of the x-intercept are (3, 0) and the entire coordinates of the y-intercept are (0, 8).Thus, we can check that we've found the correct equation in slope-intercept form by plugging in (3, 0) and (0, 8) for (x, y), -8/3 for m, and 8 for b and seeing if we get the same answer on both sides of the equation when simplifying:
Plugging in (3, 0) for (x, y) along with -8/3 for m and 8 for b:
0 = -8/3(3) + 8
0 = -24/3 + 8
0 = -8 = 8
0 = 0
Plugging in (0, 8) for (x, y) along with -8/3 for m and 8 for b;
8 = -8/3(0) + 8
8 = 0 + 8
8 = 8
Thus, the equation we've found is correct as it contains the points (3, 0) and (0, 8), which are the x and y intercepts.
You apply the
{Select)
operation
[ Select ]
-for multiplication equations and
[ Select ]
for division equations
-to
[ Select ]
of the equation.
Answers
Answer:
ndhduejcijgisjcidjcjzjfjidjicjdici djcojzifcjdjcu
Step-by-step explanation:
no se weydgfds
There are 8 students performing in the holiday concert. Of the students, 5 are boys. What decimal represents the fraction of the students that are boys (5/8)
Answers
Answer:
0.625
5/8 converted to decimal form is 0.625
if y= x+3/6-x, what is the value of y when x =7i?
Answers
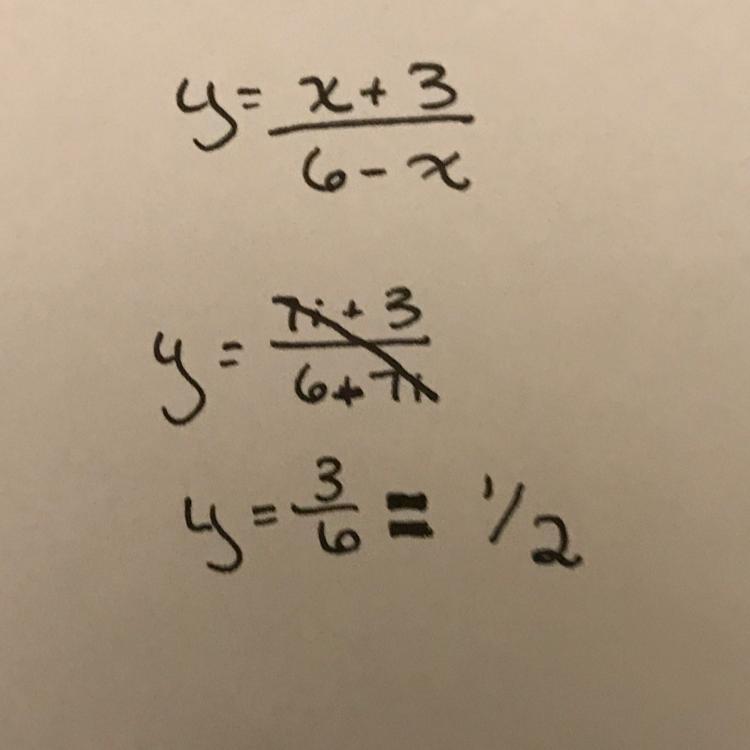
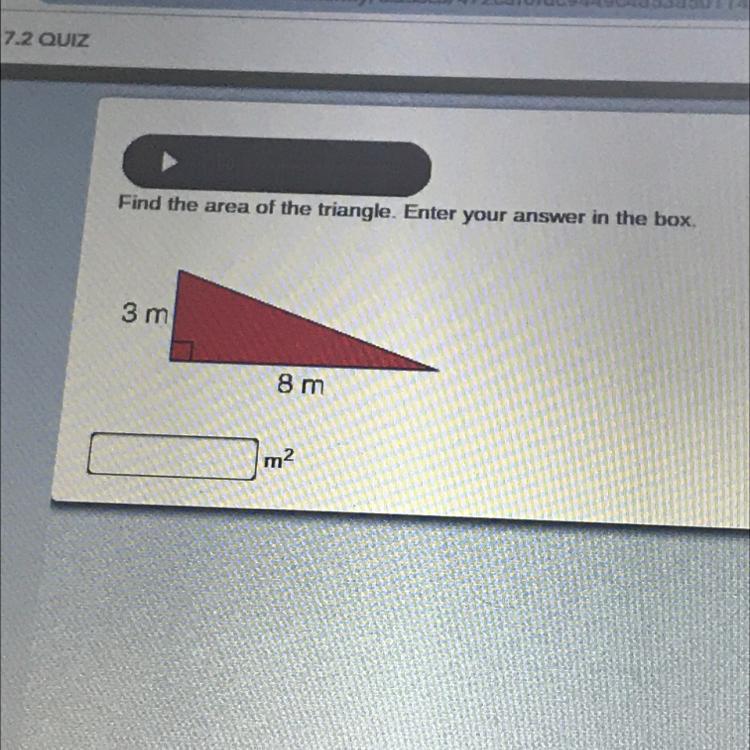
Find the area of the triangle. Enter your answer in the box.
3 m
8 m
m2
(Please help)
Answers
1/2Base×height
Step-by-step explanation:
1/2×8×3
=4×3
=12
Please solve this
∫ (log(1 + x ^ 2))/((x + 1) ^ 2) dx
Answers
The final result of the integral is:
∫ (log(1 + x²) / (x + 1)²) dx = log(x + 1) - 2 (log(x + 1) / x) - 2Li(x) + C,
where Li(x) is the logarithmic integral function and C is the constant of integration.
We have,
To solve the integral ∫ (log(1 + x²) / (x + 1)²) dx, we can use the method of substitution.
Let's substitute u = x + 1, which implies du = dx. Making this substitution, the integral becomes:
∫ (log(1 + (u-1)²) / u²) du.
Expanding the numerator, we have:
∫ (log(1 + u² - 2u + 1) / u²) du
= ∫ (log(u² - 2u + 2) / u²) du.
Now, let's split the logarithm using the properties of logarithms:
∫ (log(u² - 2u + 2) - log(u²)) / u² du
= ∫ (log(u² - 2u + 2) / u²) du - ∫ (log(u²) / u²) du.
We can simplify the second integral:
∫ (log(u²) / u²) du = ∫ (2 log(u) / u²) du.
Using the power rule for integration, we can integrate both terms:
∫ (log(u² - 2u + 2) / u²) du = log(u² - 2u + 2) / u - 2 ∫ (log(u) / u³) du.
Now, let's focus on the second integral:
∫ (log(u) / u³) du.
This integral does not have a simple closed-form solution in terms of elementary functions.
It can be expressed in terms of a special function called the logarithmic integral, denoted as Li(x).
Therefore,
The final result of the integral is:
∫ (log(1 + x²) / (x + 1)²) dx = log(x + 1) - 2 (log(x + 1) / x) - 2Li(x) + C,
where Li(x) is the logarithmic integral function and C is the constant of integration.
Learn more about integrations here:
https://brainly.com/question/30217024
#SPJ1
What is the actual distance of 9 cm on a map whose scale shows that 3 cm = 5 km?
A) 15 km
B) 12 km
C) 18 km
D) 21 km
Answers
Answer:
\(\boxed{15 km}\)
Step-by-step explanation:
→ Write out the scale
3 cm = 5 km
→ Multiply everything by 3 to get 9 cm on the left side
9 cm = 15 km
. Suppose a government agency has a monopoly in the provision of internet connections.
The marginal cost of providing internet connections is 1
2
, whereas the inverse demand
function is given by: p = 1
Answers
The government agency as a monopolist will produce and sell internet connections up to the point where the marginal cost is 1/2. The price will be set at 1, given the perfectly elastic demand function.
In the scenario where a government agency has a monopoly in the provision of internet connections and the inverse demand function is given by p = 1, we can analyze the market equilibrium and the implications for pricing and quantity.
The inverse demand function, p = 1, implies that the market demand for internet connections is perfectly elastic, meaning consumers are willing to purchase any quantity of internet connections at a price of 1. As a monopolist, the government agency has control over the supply of internet connections and can set the price to maximize its profits.
To determine the optimal pricing and quantity, the monopolist needs to consider the marginal cost of providing internet connections. In this case, the marginal cost is given as 1/2. The monopolist will aim to maximize its profits by equating marginal cost with marginal revenue.
Since the inverse demand function is p = 1, the revenue received by the monopolist for each unit sold is also 1. Therefore, the marginal revenue is also 1. The monopolist will produce up to the point where marginal cost equals marginal revenue, which in this case is 1/2.
As a result, the monopolist will produce and sell internet connections up to the quantity where the marginal cost is 1/2. The monopolist will set the price at 1 since consumers are willing to pay that price.
For more such question on monopolist. visit :
https://brainly.com/question/28336090
#SPJ8
If RAMS is a rectangle and RM = x² + 5x and AS = 11x + 16 and RA = x² + 15. Find x and find RA.
Answers
what kind of witchcraft is this?
What are the solution(s) of the quadratic equation 98 - x2 = 0?
O x = +2/7
O x = +673
O x = +7/2
O no real solution
Answers
Answer:
Solutions are x=7 square 2
The solutions of the quadratic equation 98 - x² = 0 are ±7√2.
What are Quadratic Equations?Quadratic expressions are polynomial equations of second degree.
The general form of a quadratic equation is ax² + b x + c = 0.
Given quadratic equation is,
98 - x² = 0
This can be written as,
98 = x², or
x² = 98
Now, taking the square root on both sides,
√x² = √98
x = √98
Write 98 as the product of perfect square.
98 = 49 × 2
√98 = √(49 × 2) = √49 × √2 = ±7√2
Hence the solutions are ±7√2.
Learn more about Quadratic Equations here :
https://brainly.com/question/19037377
#SPJ5
can you guys pls tell how this person got this math proplem.

Answers
by the help of calculator
Cellular phone usage grew about 22% each year from 1995 (about 34 million) to 2003. Write a function to model cellular phone usage over that time period. What is the cellular usage in 2003?
Answers
Answer:
Given the information you provided, we can model cellular phone usage over time with an exponential growth model. An exponential growth model follows the equation:
`y = a * b^(x - h) + k`
where:
- `y` is the quantity you're interested in (cell phone usage),
- `a` is the initial quantity (34 million in 1995),
- `b` is the growth factor (1.22, representing 22% growth per year),
- `x` is the time (the year),
- `h` is the time at which the initial quantity `a` is given (1995), and
- `k` is the vertical shift of the graph (0 in this case, as we're assuming growth starts from the initial quantity).
So, our specific model becomes:
`y = 34 * 1.22^(x - 1995)`
To find the cellular usage in 2003, we plug 2003 in for x:
`y = 34 * 1.22^(2003 - 1995)`
Calculating this out will give us the cellular usage in 2003.
Let's calculate this:
`y = 34 * 1.22^(2003 - 1995)`
So,
`y = 34 * 1.22^8`
Calculating the above expression gives us:
`y ≈ 97.97` million.
So, the cellular phone usage in 2003, according to this model, is approximately 98 million.
First if is an Eigenvector of the matrix A with Eigenvalue 4, will also be an Eigenvalue for any linear combination of the matrix A.
Answers
When the matrices A and B commute, or when they fulfill AB=BA, this is a significant exception.
What is matrix?
A matrix is a rectangular array or table of numbers, symbols, or formulae used to represent mathematical objects or qualities of such things. It is often arranged in rows and columns. For instance, a matrix contains two rows and three columns. a group of integers organized in a rectangular array in rows and columns. Matrix elements or entries refer to numbers. In several disciplines of engineering, physics, economics, statistics, and mathematics, matrices have a wide range of applications.
The eigenvalues and eigenvectors of the sum of two matrices are typically not the same as the sums of the eigenvalues and eigenvectors of the individual matrices. In actuality, there is no way to separate the eigenvalues of A and B from one another.
When a vector v is an eigenvector of both A and B, it is also an eigenvector of A+B, with an eigenvalue equal to the sum of its eigenvalues for A and B, respectively. There is, however, no reason to anticipate that two matrices will share an eigenvector in general. There is no method to create an eigenvector of A+B from two random eigenvectors of A and B alone.
When the matrices A and B commute, or when they fulfill AB=BA, this is a significant exception. In this situation, their invariant spaces coincide, and if both of them are diagonalizable, they are concurrently diagonalizable, which means that their eigenvectors do as well. As was already noted, in this specific instance, the eigenvectors of A+B are likewise the same.
To know more about matrix visit:
https://brainly.com/question/29132693
#SPJ4
one card is drawn from a pack of 52cards each of the 52 cards being equally likely to be drawn. what is the probability that the card drawn is a king?
Answers
The probability of drawing a king from a standard deck of 52 cards is 1/13.
In a standard deck of 52 playing cards, there are four kings: the king of hearts, the king of diamonds, the king of clubs, and the king of spades.
To find the probability of drawing a king, we need to determine the ratio of favorable outcomes (drawing a king) to the total number of possible outcomes (drawing any card from the deck).
The total number of possible outcomes is 52 because there are 52 cards in the deck.
The favorable outcomes, in this case, are the four kings.
Therefore, the probability of drawing a king is given by:
Probability = (Number of favorable outcomes) / (Number of possible outcomes)
= 4 / 52
= 1 / 13
Thus, the probability of drawing a king from a standard deck of 52 cards is 1/13.
This means that out of every 13 cards drawn, on average, one of them will be a king.
It is important to note that the probability of drawing a king remains the same regardless of any previous cards that have been drawn or any other factors.
Each draw is independent, and the probability of drawing a king is constant.
For similar question on probability.
https://brainly.com/question/7965468
#SPJ8
The Rose garden is formed by joining the rectangle in the semicirculation below the rectangle is 22 ft long and 18 ft wide if the gardener wants to build a fence around the garden how many feet of fences required
Answers
First, let's find the area of the rectangle.We know that the area of a rectangle is the length times width, or 20⋅32in this example:20⋅32=640So the area of the rectangle is 640ft2.You may not know the area of a semicircle, but that's fine −we know the area of a circle, or πr2.Since the area of a semicircle is half the area of a circle, we just do the area of the circle divided by 2:So the area of a semicircle is πr22.The question asks for πto just be 3.14, so instead the equation is A=3.14r22The picture gives the diameter of the circle.To find the radius, or r, we divide the diameter by 2:202=10Now we can solve for the area of the semicircle:3.14(10)223.14(100)23142157ft2Now that we now the areas of the rectangle and semicircle, we can add them up to find the area of the rose garden:640+157=797ft2
The values in the table represent the graph of a continuous function. Which interval must contain an x-intercept? x y –3.1 –1.85 –2.7 –0.84 –2.3 –0.09 –1.9 0.44 –1.5 0.79 –1.1 1.00 –0.7 1.10 –0.3 1.13 0.1 1.13 –3.1 < x < –2.7 –2.3 < x < –1.9 –1.5 < x < –1.1 –0.3 < x < 0.1
Answers
Given:
The values in the table represent the graph of a continuous function.
To find:
The interval that must contain an x-intercept.
Solution:
From the given table it is clear that, initially y-values are negative but after negative values we get y=0.44 at x=-1.9.
This signs of y-value are different, it means the graph of continuous function must contain an x-intercept in the interval -2.3 < x < -1.9.
Therefore, the correct option is B.
Answer:
Its , -2.3 < x < -1.9
Step-by-step explanation:
Edge 2020
Solve the given proportion X/4 = 3/6 X=
Answers
Answer:
X/4=3/6
Start off by cross multiplying the tops and bottoms, so X/4=3/6 turns into 6X=12. Now divide by 6 on both sides.
6X=12 X=2
Answer:
2
Step-by-step explanation:
Cross Multiple and Divide
X. 3
----. = ----
4. 6
So what you want to do is multiply diagonally:
(6)(X) = 6X
(3)(4) = 12
Now that we have our two answers, we put an equal sign between them.
6X = 12
Now to get X alone. Since it's being multiplied by 6, you want to do the opposite and divide.
So remember to divide on both sides to get rid of the 6.
6X divided by 6 is just X.
12 divided by 6 is 2
We got our answers, put the equal sign in-between
X = 2
Evaluate the limit
\(\lim \limits_{x\to 0} \dfrac{\ln \left(1-\dfrac x4 \right) - (1-x)^{\tfrac 14} +1}{x^2}\)
Answers
Answer:
1/16
Step-by-step explanation:
Place x=0 and you can see \(\frac{0}{0}\) indefinitness. So you can apply the l'hosptial rule. Its basic you should
\(\lim_{x \to \ 0} \frac{g(x)}{f(x)} = \\\) \(lim_{x \to \ 0} \frac{g'(x)}{f'(x)}\) so apply the derivative
\(\frac{\frac{1}{x-4} +\frac{1}{\sqrt[4]{(1-x})^3 } }{2x}\) and replace the x=0 and you'll see same answer \(\frac{0}{0}\) re-apply the l'hospital rule and answer
\(\frac{\frac{-1}{(x-4)^2} + \frac{3}{16\sqrt[4]{(1-x)^7} } }{2}\) and replace the 0 you can see the answer \(\frac{1}{16}\)
please answer question

Answers
Answer:
given below.Step-by-step explanation:
for f(x):
0
2
2√2
4
for g(x):
2
2√2
2√3
2√5
for h(x):
4
6
4+2√2
8
In planning her retirement, Liza deposits some money at 4% interest, with twice as much deposited at 4.5%. Find the amount deposited at each rate if the total annual interest income is $2080.
She deposited $___ at 4% and $____ at 4.5%.

Answers
She deposited $16,000 at 4% and $32,000 at 4.5%
She deposited $16,000 at 4% and $32,000 at 4.5%.
Let's assume Liza deposited an amount x at 4% interest. According to the given information, she deposited twice as much, which is 2x, at 4.5% interest.
To calculate the interest income from the deposits, we'll use the formula: Interest = Principal × Rate × Time.
At 4% interest, the interest earned is 0.04x (4% expressed as a decimal multiplied by x).
At 4.5% interest, the interest earned is 0.045(2x) (4.5% expressed as a decimal multiplied by 2x).
We know that the total annual interest income is $2080. Therefore, we can write the equation:
0.04x + 0.045(2x) = 2080
Simplifying the equation:
0.04x + 0.09x = 2080
0.13x = 2080
x = 2080 / 0.13
x ≈ 16,000
Liza deposited approximately $16,000 at 4% interest, and since she deposited twice as much at 4.5% interest, she deposited approximately $32,000 at 4.5% interest.
Therefore, she deposited $16,000 at 4% and $32,000 at 4.5%.
To know more about deposited:
https://brainly.com/question/32783793
#SPJ6
Referring to the figure, find P to the nearest degree.
a. 21°
b. 23°
c. 67°
d. 69°
