-3x-4y=-1 3x-y=-4 elimination
Answers
Answer:
(- 1, 1 )
Step-by-step explanation:
- 3x - 4y = - 1 → (1)
3x - y = - 4 → (2)
add (1) and (2) term by term to eliminate x
0 - 5y = - 5
- 5y = - 5 ( divide both sides by - 5 )
y = 1
substitute y = 1 into either of the 2 equations and solve for x
substituting into (2)
3x - 1 = - 4 ( add 1 to both sides )
3x = - 3 ( divide both sides by 3 )
x = - 1
solution is (- 1, 1 )
Related Questions
Find the HCF of the following by long divosiin method 102,68,136
Answers
Answer:
102=2*3*17
68=2*2*17
136=2*2*2*2*17
The common prime factors are 2 and 17
Highest common factor (HCF)=2*17=34
Hope it helps you.For 68: 1, 2, 4, 17, 34, and 68
For 136: 1, 2, 4 , 8, 17, 34, 68, and 136.
So my answer I think is: 68
convert 3 * 10 raise to power 8 m per second to kilometres per hour
Answers
Answer:
\(\huge\boxed{3\cdot10^8\dfrac{m}{s}=1.08\cdot10^9\dfrac{km}{h}}\)
Step-by-step explanation:
\(3\cdot10^8\dfrac{m}{s}\\\\1km=1,000m\to1m=0.001km\\1h=3,600s\to1s=\dfrac{1}{3600}h\)
therefore
\(3\cdot10^8\dfrac{m}{s}=3\cdot100,000,000\cdot\dfrac{\frac{1}{1000}km}{\frac{1}{3600}s}=300,000,000\cdot\dfrac{1}{1000}\cdot\dfrac{3600}{1}\dfrac{km}{h}\\\\=\dfrac{300,000,000\cdot3,600}{1,000}\dfrac{km}{h}=300,000\cdot3,600\dfrac{km}{h}=1,080,000,000\dfrac{km}{h}\\\\=1.08\cdot10^9\dfrac{km}{h}\)
Please help me solve this plsss

Answers
Answer:
no
Step-by-step explanation:
the sum of all 3 angles does not add up to 180 degrees, so no
The defect length of a corrosion defect in a pressurized steel pipe is normally distributed with mean value 28 mm and standard deviation 7.6 mm.(a)What is the probability that defect length is at most 20 mm
Answers
Answer:
14.69% probability that defect length is at most 20 mm
Step-by-step explanation:
When the distribution is normal, we use the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
In this question, we have that:
\(\mu = 28, \sigma = 7.6\)
What is the probability that defect length is at most 20 mm
This is the pvalue of Z when X = 20. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{20 - 28}{7.6}\)
\(Z = -1.05\)
\(Z = -1.05\) has a pvalue of 0.1469
14.69% probability that defect length is at most 20 mm
This data is from a sample. Calculate the mean, standard deviation, and variance. Suggestion: use technology. Round answers to two decimal places.
x
22.8
49.8
17.5
44.1
33.2
20.6
43.2
37.7
Mean =
Standard Deviation =
Variance =
Ooops - now you discover that the data was actually from a population! So now you must give the population standard deviation.
Population Standard Deviation =
Answers
1. Mean = 33.61
2. Standard Deviation = 11.3284
3. Variance = 128.33
What are the mean, standard deviation, and variance?The given data are: \(22.8, 49.8, 17.5, 44.1, 33.2, 20.6, 43.2, 37.7\)
To get mean, we will sum up all the numbers and divide by the total count. The mean is:
= (22.8 + 49.8 + 17.5 + 44.1 + 33.2 + 20.6 + 43.2 + 37.7) / 8
= 268.9 / 8
= 33.62
Standard Deviation: \(\sqrt((22.8 - 33.61)^2 + (49.8 - 33.61)^2 + (17.5 - 33.61)^2 + (44.1 - 33.61)^2 + (33.2 - 33.61)^2 + (20.6 - 33.61)^2 + (43.2 - 33.61)^2 + (37.7 - 33.61)^2) / 8\)
= \(\sqrt{128.3336}\)
= 11.3284420818
= 11.3284
Variance = (Standard Deviation)^2
Variance = \(11.3284 ^2\)
Variance = 128.33264656
Variance = 128.33.
Read more about measure of centres
brainly.com/question/15214370
#SPJ1
simplify this please
7^x ÷ 7^y
Answers
Answer:
\(\huge\boxed{7^{x-y}}\)
Step-by-step explanation:
We can use basic exponent rules to simplify this expression.
We know that \(a^b \div a^c = a^{b-c}\).
Since we have the same base (7) and different exponents (x, y), we can subtract the exponents and raise the base to that power.
\(7^{x-y}\)
Hope this helped!
I = V/R
make R the Subject formula
Answers
Answer:
R = V/I
Step-by-step explanation:
I = V/R
Multiply both sides by r
IR = V
Divide both sides by I
R = V/I
Ex:
2 = 6/3
3 = 6/2
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
R = V/I
Step-by-step explanation:
Let’s say that I = 8 v = 4 and r = ?
8 = 4/?
How would we solve for R?
Divide 4 by 8
R = 0.5
Please hurry due in an hour

Answers
Two cars are traveling towards a hotel on the same road. From the edge of the hotel, 600 feet high, Spiderman sits on the rooftop thinking about the depression angle needed to reach each car. If the depression angle to the nearest car is 52 degrees, and the depression angle to the farther car is 46 degrees, how far apart must the two cars be from each other?
Make a sketch, solve the problem, and round your answer to the nearest hundredth of a foot.
Answers
The two cars must be approximately 177.34 feet apart from each other for Spiderman to have different depression angles to each car.
To find the distance between the two cars, we can use trigonometry and the concept of similar triangles. Let's denote the distance between Spiderman and the nearest car as d1 and the distance between Spiderman and the farther car as d2.
In a right triangle formed by Spiderman, the height of the hotel, and the line of sight to the nearest car, the tangent of the depression angle (52 degrees) can be used:
tan(52) = 600 / d1
Rearranging the equation to solve for d1:
d1 = 600 / tan(52)
Similarly, in the right triangle formed by Spiderman, the height of the hotel, and the line of sight to the farther car, the tangent of the depression angle (46 degrees) can be used:
tan(46) = 600 / d2
Rearranging the equation to solve for d2:
d2 = 600 / tan(46)
Using a calculator, we can compute:
d1 ≈ 504.61 feet
d2 ≈ 681.95 feet
The distance between the two cars is the difference between d2 and d1:
Distance = d2 - d1
Plugging in the values, we have:
Distance ≈ 681.95 - 504.61
Distance ≈ 177.34 feet
For more such question on angles. visit :
https://brainly.com/question/25770607
#SPJ8
Estimate 1.19 and 12
Answers
Answer:
The unit rate is about 10 cents per fluid once of grape of juice.
Step-by-step explanation:
Sketch a graph of f(x)={- 5 if x < -2 2x-1 if-2 < x≤ 2 0 if x>2. (piecewise)
Answers
A graph of the given piecewise-defined function is shown in the image below.
What is a piecewise-defined function?In Mathematics and Geometry, a piecewise-defined function simply refers to a type of function that is defined by two (2) or more mathematical expressions over a specific domain.
Generally speaking, the domain of any piecewise-defined function simply refers to the union of all of its sub-domains. By critically observing the graph of this piecewise-defined function, we can reasonably infer and logically deduce that it is constant over several intervals or domains such as x > 2 and x < -2.
In conclusion, this piecewise-defined function has a removable discontinuity.
Read more on piecewise function here: brainly.com/question/18670055
#SPJ1

Find the measure. m∠GDF

Answers
Answer:
∠GDF = 26°
Step-by-step explanation:
6y + 2 = 7y - 2
subtract 6y from each side of the equation:
2 = y - 2
add 2 to each side:
y = 4
6(4) + 2 = 26°
When Amella started painting, the paint can had 7/8 gallon in it. She used 3/8 gallons How much paint is left in the can?
Answers
Answer: If Amella started with 7/8 gallon of paint in the can and used 3/8 gallons, then the amount of paint left in the can can be found by subtracting the amount used from the amount started with:
Amount left = Amount started with - Amount used
Amount left = 7/8 - 3/8
Amount left = 4/8 or 1/2 gallon
Therefore, Amella has 1/2 gallon of paint left in the can.
Step-by-step explanation:
each year america.edu ranks the best paying college degrees in america. the following data show the median starting salary, the mid-career salary, and the percentage increase from starting salary to mid-career salary for the college degrees with the highest mid-career salary (america.edu website). click on the datafile logo to reference the data. degree starting salary mid-career salary % increase aerospace engineering 59,400 108,000 82 applied mathematics 56,400 101,000 79 biomedical engineering 54,800 101,000 84 chemical engineering 64,800 108,000 67 civil engineering 53,500 93,400 75 computer engineering 61,200 87,700 43 computer science 56,200 97,700 74 construction management 50,400 87,000 73 economics 48,800 97,800 100 electrical engineering 60,800 104,000 71 finance 47,500 91,500 93 government 41,500 88,300 113 information systems 49,300 87,100 77 management info. systems 50,900 90,300 77 mathematics 46,400 88,300 90 nuclear engineering 63,900 104,000 63 petroleum engineering 93,000 157,000 69 physics 50,700 99,600 96 software engineering 56,700 91,300 61 statistics 50,000 93,400 87
Answers
Construct the histogram for the percentage increase in the starting salary by using 10 as the class width.
Answer Output using MINITAB software is given below at the end of answer (bar graph)
Frequency:
The frequencies are calculated by using the tally mark and the range of the starting salary is grouped and the range is from 40 to 120. Here the number of times each percentage increase repeats is the frequency of that particular class.
The width of class is 10.
Make a tally mark for each value in the corresponding revenue class and continue for all values in the data.
The number of tally marks in each class represents the frequency, f of that class.
Similarly, the frequency of remaining classes for the percentage increase is given below at the end of the answer.
The data represents the median starting salary, the mid-career salary, and the percentage increase from starting salary to mid-career salary for the 20 college degrees with the highest mid-career salary.
For more such questions on Graphical representation
https://brainly.com/question/29956598
#SPJ4


Select the correct answer from each drop-down menu.
The total area of the three triangles is
square units.
The area of the figure is
square units.
Answers
The total area of the three triangles is square units is 36 and the area of the figure is square units is 60.
What is the triangle?The triangle can be defined as a three-sided polygon in geometry, and it consists of three vertices and three edges. The sum of all the angles inside the triangle is 180°.
From the figure, the area of triangles can be calculated using the:
Area = (1/2)height×base length
Area of three triangle = 1/2(4×6) + 1/2(6×4) + 1/2(4×6)
Area of three triangle = 1/2(24×3) = 36 square units
Area of the figure = area of three triangle + area of the rectangle
= 36 + 6×4
= 60 square units
Thus, the total area of the three triangles is square units is 36 and the area of the figure is square units is 60.
Learn more about the triangle here:
brainly.com/question/25813512
#SPJ1

Determine whether the relation is a function. Explain. x y 4 –5 –1 –10 0 –9 1 –7 9 1 Multiple choice question. cross out A) Yes; for each element of the domain, there is only one element of the range. cross out B) Yes; for each element of the range, there is only one element of the domain. cross out C) No; the element 1 is in both the domain and the range. cross out D) No; for each element of the domain, there is not only one element of the range.
Answers
It is not a function because: C) the element 1 is in both the domain and the range.
What makes a Relation a Function?A relation can be defined as a function if each of the domain values each has exactly one corresponding range value. This means that an element of the domain must not have two different elements from the range that it is related or corresponded to.
In the given function, 1 as an element of the domain is related to two different range elements, 10 and 7. This doesn't satisfy a function property.
Therefore, we can state that: it is not a function because: C) the element 1 is in both the domain and the range.
Learn more about function on:
https://brainly.com/question/15602982
#SPJ1
Find non-invertible matrices A,B such that A+B is invertible. Choose A,B so that (1) neither is a diagonal matrix and (2) A,B are not scalar multiples of each other.A = [_____ _____][_____ _____]B = [_____ _____][_____ _____]
Answers
Matrices A and B are non-invertible matrices that can be added together to form an invertible matrix. To find these matrices, we can use the following steps:
Step 1: Choose a matrix A that is not a diagonal matrix and is not invertible. One example of such a matrix is
\(A = \left[\begin{array}{ccc}1&1\\0&0\end{array}\right]\)
Step 2: Choose a matrix B that is not a diagonal matrix, is not invertible, and is not a scalar multiple of matrix A. One example of such a matrix is
\(B = \left[\begin{array}{ccc}0&0\\1&1\end{array}\right]\)
Step 3: Add the matrices A and B together to form the matrix A+B. This matrix will be invertible, as shown below:
\(A+B = \left[\begin{array}{ccc}1&1\\0&0\end{array}\right]+\left[\begin{array}{ccc}0&0\\1&1\end{array}\right]=\left[\begin{array}{ccc}1&1\\1&1\end{array}\right]\)
Step 4: Verify that the matrix A+B is invertible by finding its determinant. The determinant of a 2x2 matrix is given by:
det(A+B) = (1)(1) - (1)(1) = 0
Since the determinant of the matrix A+B is not equal to zero, the matrix is invertible.
Therefore, the matrices \(A = \left[\begin{array}{ccc}1&1\\0&0\end{array}\right]\) and \(B = \left[\begin{array}{ccc}0&0\\1&1\end{array}\right]\) are non-invertible matrices that can be added together to form an invertible matrix \(A+B =\left[\begin{array}{ccc}1&1\\1&1\end{array}\right]\).
https://brainly.in/question/8463680
#SPJ1
Someone help me
Find the x and y intercepts of the function

Answers
jacol jacol boy 103847wks
You cut out a piece of fabric in the shape of a kite so that the congruent angles of the kite are each
100°. Of the remaining two angles, one is 4 times larger than the other. What is the measure of the
largest angle in the kite?
Answers
The measure of the largest angle in the kite is 26.67 (approx)°.
The given problem states that you cut out a piece of fabric in the shape of a kite so that the congruent angles of the kite are each 100°. The other two angles of the kite are not equal. If one of the angles is 4 times the size of the other, then the larger angle is 4x, and the smaller one is x.
We need to determine the measure of the largest angle in the kite. In order to find out the measure of the largest angle in the kite, we need to know the sum of all the angles in the kite. Let's recall the sum of angles in a kite. A kite is a quadrilateral whose four sides can be grouped into two pairs of adjacent sides that are equal in length. A kite has two opposite pairs of equal angles. The sum of the angles of a kite is 360°.In a kite, the angles can be represented as a, a, b, and c where a is the congruent angle and b and c are non-congruent angles.
Then, 2a + 2b = 360°2a + 2x + 4x = 360°2a + 6x = 360°2a = 360° - 6x2a = 180° - 3xa = (180° - 3x)/2
Since a = 100°, we can substitute it in the equation above, a = (180° - 3x)/2 and find the value of x.
Substituting a = 100° in the above equation, we get:
100 = (180 - 3x)/2100 × 2 = 180 - 3x200 = 180 - 3x20 = -3x/-3x = -20/(-3)x = 6.67 (approx)
Now we can substitute this value of x in the expression for the larger angle to find its measure. The larger angle is 4x, so it is equal to 4(6.67) = 26.67 (approx)°.
Therefore, the measure of the largest angle in the kite is 26.67 (approx)°.
For more such questions on angle , Visit:
https://brainly.com/question/25770607
#SPJ8
please help asap
i keep failing these quizzes i’m so confused

Answers
Answer:
try b
Step-by-step explanation:
I keep getting the wrong answer.

Answers
The volume of the solid obtained by rotating the region bounded by the curve y = 1 - (x - 5)² in the first quadrant about the y-axis is 51π cubic units.
What is the volume of the solid obtained by rotating the region in the first quadrant bounded by the given curve about the y - axis?To find the volume of the solid obtained by rotating the region bounded by the curve y = 1 - (x - 5)² in the first quadrant about the y-axis, we can use the method of cylindrical shells.
The formula for the volume using cylindrical shells is:
V = 2π ∫ [a, b] x * h(x) dx
Where:
- V is the volume of the solid
- π represents the mathematical constant pi
- [a, b] is the interval over which we are integrating
- x is the variable representing the x-axis
- h(x) is the height of the cylindrical shell at a given x-value
In this case, we need to solve for x in terms of y to express the equation in terms of y.
Rearranging the given equation:
x = 5 ± √(1 - y)
Since we are only interested in the region in the first quadrant, we take the positive square root:
x = 5 + √(1 - y)
Now we can rewrite the volume formula with respect to y:
V = 2π ∫ [c, d] x * h(y) dy
Where:
- [c, d] is the interval of y-values that correspond to the region in the first quadrant
To determine the interval [c, d], we set the equation equal to zero and solve for y:
1 - (x - 5)² = 0
Expanding and rearranging the equation:
(x - 5)² = 1
x - 5 = ±√1
x = 5 ± 1
Since we are only interested in the region in the first quadrant, we take the value x = 6:
x = 6
Now we can evaluate the integral to find the volume:
V = 2π ∫ [0, 1] x * h(y) dy
Where h(y) represents the height of the cylindrical shell at a given y-value.
Integrating the expression:
V = 2π ∫ [0, 1] (5 + √(1 - y)) * h(y) dy
To find h(y), we need to determine the distance between the y-axis and the curve at a given y-value. Since the curve is symmetric, h(y) is simply the x-coordinate at that point:
h(y) = 5 + √(1 - y)
Substituting this expression back into the integral:
V = 2π ∫ [0, 1] (5 + √(1 - y)) * (5 + √(1 - y)) dy
Now, we can evaluate this integral to find the volume
V = 2π ∫ [0, 1] (5 + √(1 - y)) * (5 + √(1 - y)) dy
To simplify the integral, let's expand the expression:
V = 2π ∫ [0, 1] (25 + 10√(1 - y) + 1 - y) dy
V = 2π ∫ [0, 1] (26 + 10√(1 - y) - y) dy
Now, let's integrate term by term:
\(V = 2\pi [26y + 10/3 * (1 - y)^\frac{3}{2} - 1/2 * y^2]\)] evaluated from 0 to 1
V = \(2\pi [(26 + 10/3 * (1 - 1)^\frac{3}{2} - 1/2 * 1^2) - (26 * 0 + 10/3 * (1 - 0)^\frac{3}{2} - 1/2 * 0^2)]\)
V = 2π [(26 + 0 - 1/2) - (0 + 10/3 - 0)]
V = 2π (25.5)
V = 51π cubic units
Learn more on volume of a solid obtained by rotating curve here;
https://brainly.com/question/32301706
#SPJ1
A family's monthly income is $41360. The family spends 3 over 8 of this on food. How much is spent on food
Answers
Answer:
$15,510.00
Step-by-step explanation:
\(\frac{3}{8}\) x \(\frac{41360}{1}\) = \(\frac{124080}{8}\)= 15510
Divide
During halftime of a basketball game, a sling shot launches T-shirts at the crowd. A T shirt is launched from a heigh of 4 feet with an initial upward velocity of 72 feet per second. Use the equation h(t)= -16t^2+72t+4, where t is time in seconds and h(t) is height. How long will it take the T shirt to reach its maximum height? What is the maximum height?

Answers
During halftime of a basketball game, a slingshot launches T-shirts at the crowd.
it takes the T-shirt 9/4 secondsThe maximum height of the T-shirt is 77 feet.What is the maximum height?
Generally, To find the time it takes the T-shirt to reach its maximum height, we need to find the time when the height of the T-shirt stops increasing and starts decreasing. At this point, the velocity of the T-shirt will be 0, since it is not moving up or down.
The velocity of the T-shirt at any time t can be found by taking the derivative of the equation for height:
v(t) = dh/dt = -32t + 72
Setting the velocity to 0 and solving for t, we get:
0 = -32t + 72 32t = 72 t = 72/32 t = 9/4
So it takes the T-shirt 9/4 seconds, or approximately 2.25 seconds, to reach its maximum height.
To find the maximum height, we plug this value back into the equation for height:
h(t) = -16(9/4)^2 + 72(9/4) + 4 h(t) = -81 + 162 + 4 h(t) = 77
The maximum height of the T-shirt is 77 feet.
Read more about maximum height heighthttps://brainly.com/question/6261898
#SPJ1
HELP AS SOON AS POSSIBLE

Answers
The coordinates of polygon A'B'C'D' after the rotation of 180º are given as follows:
A'(0,0), B'(-5,-2), C'(-5,5), D'(0,3).
What are the rotation rules?The five more known rotation rules are given as follows:
90° clockwise rotation: (x,y) -> (y,-x).90° counterclockwise rotation: (x,y) -> (-y,x).180° clockwise and counterclockwise rotation: (x, y) -> (-x,-y).270° clockwise rotation: (x,y) -> (-y,x).270° counterclockwise rotation: (x,y) -> (y,-x).The original coordinates for this problem are given as follows:
A(0,0), B(5,2), C(5,-5), D(0,-3).
Exchanging the sign of each of the coordinates, the coordinates after the rotation are given as follows:
A'(0,0), B'(-5,-2), C'(-5,5), D'(0,3).
More can be learned about rotation rules at brainly.com/question/17042921
#SPJ1
Ajay leans à 18-foot ladder against a wall so that it forms an angle of 73° with
the ground. How high up the wall does the ladder reach? Round your answer
to the nearest tenth of a foot if necessary.
Answers
Check the picture below.

The ladder reaches 17.2-foot high up the wall.
Given that,
Ajay leans à 18-foot ladder against a wall so that it forms an angle of 73° with the ground.
We have to find,
How high up the wall does the ladder reach?
According to the question,
Ajay leans à 18-foot ladder against a wall so that it forms an angle of 73° with the ground.
Let, the height of the wall does the ladder reach is y,
Then,
\(\rm Sin\theta = \dfrac{Opposite \ side}{Hypotenuse}\)
Here, Angle = 17 degree, opposite side = y, and perpendicular = 18
Therefore,
\(\rm Sin73 = \dfrac{y}{18}\\\\0.95 = \dfrac{y}{18}\\\\y = 18 \times 0.95\\\\y = 17.2 \ foot\)
Hence, The ladder reaches 17.2-foot high up the wall.
For more details refer to the link.
https://brainly.com/question/2016644
one card is drawn from a pack of 52cards each of the 52 cards being equally likely to be drawn. what is the probability that the card drawn is a king?
Answers
The probability of drawing a king from a standard deck of 52 cards is 1/13.
In a standard deck of 52 playing cards, there are four kings: the king of hearts, the king of diamonds, the king of clubs, and the king of spades.
To find the probability of drawing a king, we need to determine the ratio of favorable outcomes (drawing a king) to the total number of possible outcomes (drawing any card from the deck).
The total number of possible outcomes is 52 because there are 52 cards in the deck.
The favorable outcomes, in this case, are the four kings.
Therefore, the probability of drawing a king is given by:
Probability = (Number of favorable outcomes) / (Number of possible outcomes)
= 4 / 52
= 1 / 13
Thus, the probability of drawing a king from a standard deck of 52 cards is 1/13.
This means that out of every 13 cards drawn, on average, one of them will be a king.
It is important to note that the probability of drawing a king remains the same regardless of any previous cards that have been drawn or any other factors.
Each draw is independent, and the probability of drawing a king is constant.
For similar question on probability.
https://brainly.com/question/7965468
#SPJ8
What is the slope of the line that represents this relationship?
Graph the line that represents this relationship.

Answers
The line parallel to the x-axis passing through the points (5,5) and (-5,5) has a slope of 0, indicating a horizontal line with a constant y-coordinate value of 5.
To determine the slope of the line that represents this relationship, we can use the formula for slope, which is given by:
slope = (change in y-coordinates) / (change in x-coordinates)
In this case, we are given two points on the line: (5,5) and (-5,5).
The change in y-coordinates is 5 - 5 = 0, as the y-coordinate remains constant.
The change in x-coordinates is -5 - 5 = -10.
Substituting these values into the slope formula, we get:
slope = 0 / -10 = 0
Therefore, the slope of the line that represents this relationship is 0.
A slope of 0 indicates that the line is parallel to the x-axis. This means that the line has a constant y-coordinate value for all x-coordinate values. In this case, the line passes through the point (5,5) and (-5,5), and it remains at y = 5 for all x-values.
Visually, a line with a slope of 0 would be a horizontal line on the coordinate plane. It does not have an upward or downward slope but remains parallel to the x-axis.
It's important to note that the slope of 0 indicates a relationship where the dependent variable (y) does not change with respect to the independent variable (x). In this case, no matter the value of x, the corresponding y-value remains constant at 5.
For more such information on: slope
https://brainly.com/question/16949303
#SPJ8
Find area of trapezium with height 8cm and the sum of its parallel sides as 15cm
Answers
Answer:
The Area of the trapezium is \(60cm^2\)
Step-by-step explanation:
Given,
Height (h)= 8cm
Sum of the parallel sides (a+b)= 15cm
Area of trapezium = \(1/2*h*(a+b)\)
=\(1/2*8*15\)
=\(4*15\)
Area of trapezium=60cm^2
Answer: Area = 60 cm²
Step-by-step explanation:
To find the area of a trapezium we use the formula
Area of trapezium = 1/2 (sum of parallel sides) × height
∴ Area = 1/2 ×15 cm × 8 cm
= 60 cm²
To solve more questions related to the Area
https://brainly.com/question/16519513
https://brainly.com/question/76387
Linear Functions, Determining Slope
Find the slope of the line that passes through the given points. Then determine if the line is increasing,
decreasing, horizontal or vertical.
Note: If the slope does not exist, enter DNE
Ordered Pairs
Slope
Behavior
m =
(15,3) and (17,7)
Select an answer
m =
(6,0) and (8, – 8)
Select an answer
m =
(8, -7) and (12, - 7)
Select an answer
m =
(-2,- 11) and (10,49)
Select an answer
m =
(4, - 5) and (4,7)
Select an answer
Answers
i hope this helps! let me know if i got something wrong.

help with 6 please i need to graduate
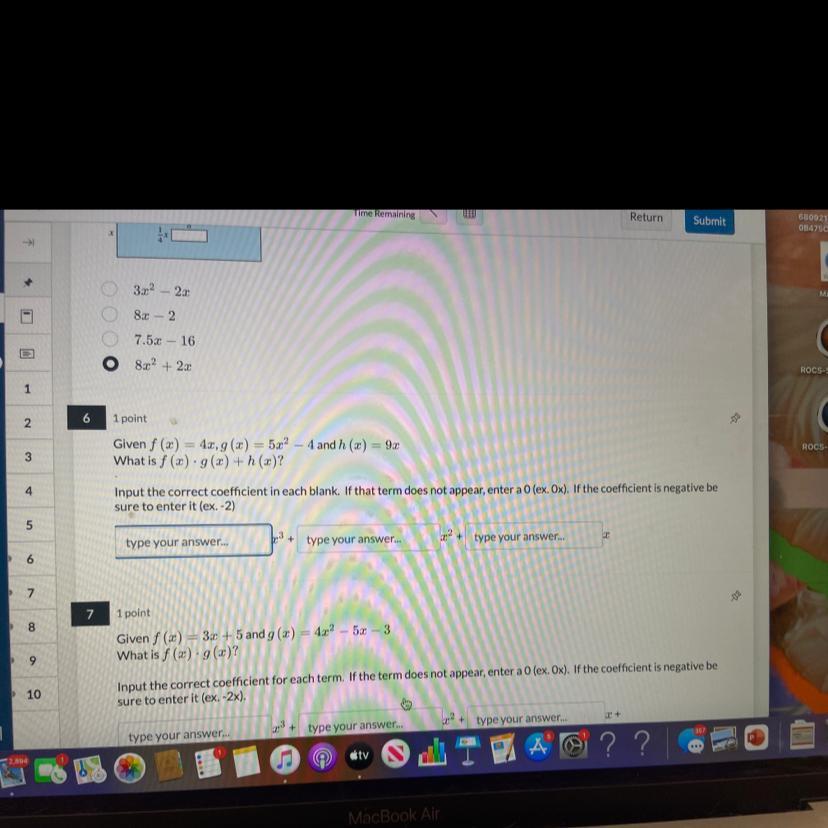
Answers
The expression with the correct coefficients in each block is given as follows:
20x³ + 0x² - 7x.
How to obtain the resultant function?The functions in the context of this problem are defined as follows:
f(x) = 4x.g(x) = 5x² - 4.h(x) = 9x.The operation is given as follows:
f(x)g(x) + h(x).
Hence, to obtain the resultant function, we apply the definitions into the operation and the simplify, applying the distributive property and combining the like terms, as follows:
4x(5x² - 4) + 9x = 20x³ - 16x + 9x = 20x³ - 7x.
As there is no x² term, the coefficient of zero multiplies the term x².
More can be learned about functions at https://brainly.com/question/31895757
#SPJ1