3a + 4 = 2a + 7 and justify your steps
Answers
Answer:
3
Step-by-step explanation:
3a-2a=7-4
a=3 the answer is 3
Related Questions
You plan on supplementing your income. you would like to withdraw a semiannual salary of $6,951.20 from an account paying 1.75% interest, compounded semiannually. determine the amount needed in the account such that you can withdraw the needed amount at the end of each period for 15 years. round to the nearest cent. a. $239,364.66 b. $182,713.25 c. $184,311.99 d. $237,288.39
Answers
The amount needed in the account is 182,713.25 dollars then the correct option is B.
What is a monthly payment?The term loan refers to a sort of credit vehicle in which a sum of money is lent to another party in exchange for the value or principal amount being repaid in the future.
Then the formula of monthly payment (MP) will be
\(\rm MP = P \times \dfrac{r(1+r)^n}{(1+r)^n - 1}\\\)
The formula can be written as
\(\rm P = MP \times \dfrac{(1+r)^n-1}{r(1+r)^n}\\\)
You plan on supplementing your income. you would like to withdraw a semiannual salary of $6,951.20 from an account paying 1.75% interest, compounded semiannually.
The amount needed in the account is such that you can withdraw the needed amount at the end of each period for 15 years will be
MP = $6951.20
r = 0.00875
n = 30
Then we have
\(\rm P = 6951.20 \times \dfrac{(1+0.00875)^{30}-1}{0.00875(1+0.00875)^{30}}\\\\P = \$182713.25\)
More about the monthly payment link is given below.
https://brainly.com/question/14064255
2) What is the slope of the line from the following table? (Please show your work)

Answers
Answer:
pick any two points
im going to chose (1,3) and (3,7)
so the equation y2-y1/x2-x1
1 = x1
3=y1
3=x2
7=y2
so 7-3/3-1 is 4/2
which is 2
36. Business A jeweler plans to produce a ring made of silver and gold. The price of
gold is about $25 per gram. The price of silver is approximately $.40 per gram. She
considers the following in deciding how much gold and silver to use in the ring.
The total mass must be more than 10 g but less than 20 g.
•The ring must contain at least 2 g of gold.
The total cost of the gold and silver must be less than $90.
a. Write and graph the inequalities that describe this situation.
b. For one solution, find the mass of the ring and the cost of the gold and silver.
Answers
The border line is so much shaded below the inequality symbol (shown in purple).
what is inequality ?A relationship among two expresses or values that is neither equal in mathematics is referred to by the term inequality. Thus, unequal results from imbalance. In arithmetic, an inequality explains the links between two non-equal numbers. Egality nor disparities are not the same. Were using the not equal symbol most usually when two values are just not equal (). Values of any size can be contrast using a variety of discrepancies. By changing the two sides till only the variables are left, many straightforward inequalities can be solved. However, a variety of factors support injustice: Both sides' negative values are split or added. Change the left and the right.
given
Gold costs $25 a gram, therefore y grams would cost $25. Because silver costs $0.40 per gram, x grams will cost you $0.0040. If the entire cost of the ring must be less than $90, then 25y+0.40x90, making the cost of the ring (25y+0.40x) dollars. For y, resolve this inequality: 25+0.40<90/25−0.40+90
Take 0.40 off of both sides.
<−0.016+3.6
25y+0.40x y900.40x+900.016x+3.6 = 25y+0.40x y900.40x+903.6
Remove 0.40x from both sides.
Add 25 to both sides.
The boundary line is therefore defined as =0.016+3.6 y=0.016x+3.6, which has a y-intercept of 3.6 and a slope of 0.016 0.016.
The border line is so much shaded below the inequality symbol (shown in purple).
To know more about inequality visit:
https://brainly.com/question/29914203
#SPJ1
Write two equations that represent the graph shown below- one equation using sine, and one equation using cosine.
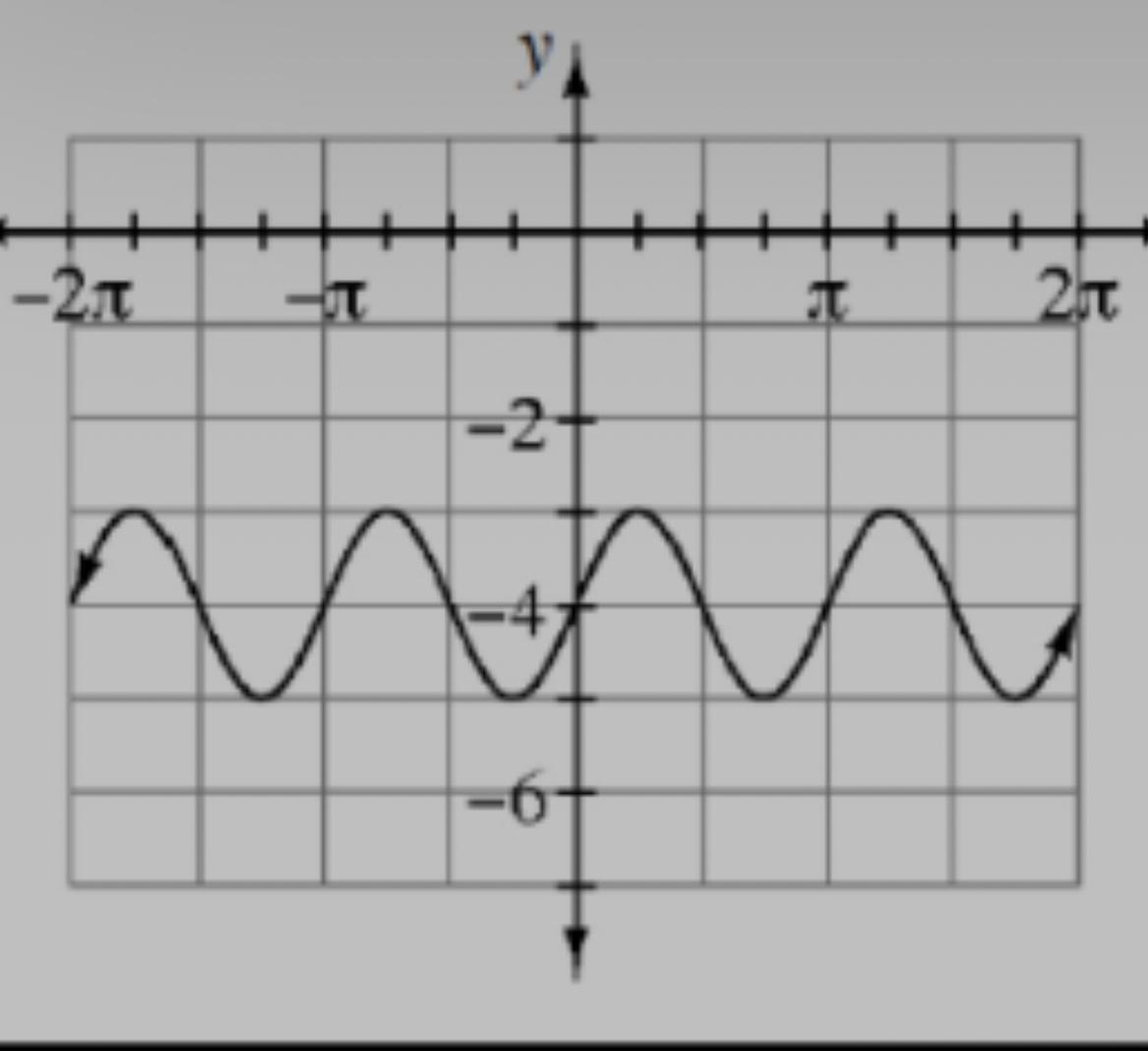
Answers
Two equations that represent the graph shown below as sine function y = 0.909x−3 and as cosine function y = −0.416x −3.
What is sine function?The sine graph or sinusoidal graph is an up-down graph and repeats every 360 degrees i.e. at 2π.
The general form of a cosine function is:
y = a cosb (θ±c) ± d
Here, amplitude, a is = 1
For b, period is = π
2π/b = π
b = 2
c = 0
vertical shift = D = -3
Putting the value into formula
y = 1 cos2 (θ + 0) - 3
y = 1 ×−0.416(θ + 0) - 3
y = −0.416θ−3
y = −0.416x −3 (cosine function)
y = 1 sin2 (θ + 0) - 3
y = 1 ×0.909(θ + 0) - 3
y = 0.909θ−3
y = 0.909x−3 (sine function)
Thus, two equations that represent the graph shown below as sine function y = 0.909x−3 and as cosine function y = −0.416x −3.
Learn more about sine function
https://brainly.com/question/12015707
#SPJ1
Use z scores to compare the given values. Based on sample data, newborn males have weights with a mean of 3247.5 g and a standard deviation of 580.3 g. Newborn females have weights with a mean of 3078.8 g and a standard deviation of 692.7 g. Who has the weight that is more extreme relative to the group from which they came: a male who weighs 1600 g or a female who weighs 1600 g? and the z score for the female is z = the has the weight that is more extreme. Since the z score for the male is z = (Round to two decimal places.)
Answers
The z-score is a standardized score that measures how many standard deviations the score is from the mean of the population. By transforming data into z-scores, we can compare and rank scores from different populations with different means and standard deviations.
Using z-scores to compare the given values, we have; The z-score for the male is; z = (1600 - 3247.5) / 580.3 = -1.88. The z-score for the female is; z = (1600 - 3078.8) / 692.7 = -2.36. The z-score is a standard score that can be used to compare values from different populations, with different means and standard deviations. We can use z-scores to determine which value is more extreme relative to the population from which it was drawn. Based on sample data, newborn males have weights with a mean of 3247.5 g and a standard deviation of 580.3 g, while newborn females have weights with a mean of 3078.8 g and a standard deviation of 692.7 g. The z-score for a male who weighs 1600 g is z = (1600 - 3247.5) / 580.3 = -1.88. Similarly, the z-score for a female who weighs 1600 g is z = (1600 - 3078.8) / 692.7 = -2.36. Since the z-score for the female is more negative, the female has a weight that is more extreme relative to the group from which they came. This means that the female weight of 1600 g is farther from the mean of the female population than the male weight of 1600 g is from the mean of the male population.
Using z-scores to compare the weights of newborn males and females, we found that a female who weighs 1600 g has a more extreme weight relative to the group from which she came than a male who weighs 1600 g. The z-score for the female was -2.36, while the z-score for the male was -1.88. The z-score is a useful tool for comparing values from different populations with different means and standard deviations.
To know more about standardized score visit:
brainly.com/question/11909387
#SPJ11
how many turtles die every year because of humans?
save the turtles
Answers
Answer:
We found, based on beach strandings, that more than 1,000 turtles are dying a year, after becoming tangled up, but this is almost certainly a gross underestimate. Young turtles and hatchings are particularly vulnerable to entanglement.” In recent years, global turtle population numbers have been falling.
the difference between two numbers is 2 and their product 80
Answers
Answer:
the numbers are 10 and 8
write the standard form equation of the circle( 7,-5)

Answers
Answer:
(x-7)²+(y+5)²=25
Step-by-step explanation:
The standard form of a circle is (x-h)²+(y-k)²=r²
(h,k) is the center
r is the radius
h=7
k=-5
r=5
(x-7)²+(y--5)²=5²
(x-7)²+(y+5)²=25
14. (10.0 points) Given f(x)=sin(2πx), when x = 0.3, f(x) = 0.951057. Approximate the value of f(0.2) using the first two terms in the Taylor series and Vx=0.1. (Write your answer to 6 decimal points).
Answers
Given the function f(x)=sin(2πx), with x = 0.3, f(x) = 0.951057. The objective is to approximate the value of f(0.2) using the first two terms in the Taylor series and Vx=0.1.
We know that the Taylor series for a function f(x) can be written as:f(x)=f(a)+f′(a)(x−a)+f′′(a)2(x−a)2+…+f(n)(a)n!(x−a)n+…The first two terms of the Taylor series are given by:f(x)=f(a)+f′(a)(x−a)The first derivative of f(x) is given by:f′(x)=2πcos(2πx)On substituting x = a = 0.1, we get:f′(0.1) = 2πcos(2π * 0.1) = 5.03118603447The value of f(x) at a=0.1 is given by:f(0.1) = sin(2π * 0.1) = 0.587785252292With a=0.1, the first two terms of the Taylor series become:f(x)=0.587785252292+5.03118603447(x−0.1) = 0.587785252292+0.503118603447x−0.503118603447×0.1Using x=0.2 and substituting the values of a and f(a) in the equation above, we get:f(0.2)=0.587785252292+0.503118603447*0.2−0.503118603447×0.1=0.712261After approximating the value of f(0.2) using the first two terms in the Taylor series,
we can conclude that the value of f(0.2) = 0.712261 with a = 0.1, with an error of approximately 0.012796.
To know more about Taylor series visit
https://brainly.com/question/32235538
#SPJ11
A candy store uses a 50% markup on cost. Find out the owners cost of a candy bar that sells for $1.50.
Answers
Answer:
The owners' cost of the candy bar is $1
Step-by-step explanation:
Assume that the owners' cost of the candy bar is 100%
∵ The owners' cost of the candy bar is 100%
∵ The candy store uses a 50% markup on cost
∵ The selling cost = owners' cost + markup
∴ The selling cost = 100% + 50% = 150%
∵ The candy bar sells for $1.50
→ That means 1.50 is 150% of the owners' cost
∴ 1.50 = 150% × owners' cost
→ Change 150% to decimal by divide it by 100
∵ 150% = 150 ÷ 100 = 1.50
∴ 1.50 = 1.50 × owners' cost
→ Divide both sides by 1.50
∴ 1 = owners' cost
∴ The owners' costs = $1
∴ The owners' cost of the candy bar is $1
help me on this please i need it now

Answers
hope this helps you !
What is the surface area of this shape?

Answers
Answer:
176
Step-by-step explanation:
ch 10 sec 5 ex 10 (b) - cross bridges can someone cross all the bridges shown in this map exactly once and return to the starting point?
Answers
In exercise 10(b) of Chapter 10, Section 5, the question asks whether it is possible to cross all the bridges shown in a given map exactly once and return to the starting point.
This problem is known as the "Seven Bridges of Königsberg" puzzle, famously solved by Leonhard Euler in the 18th century. The solution involves applying graph theory principles to analyze the connectivity and degree of the bridges. The Seven Bridges of Königsberg problem is a well-known mathematical puzzle that involves a network of bridges and islands. The goal is to determine whether it is possible to cross each bridge exactly once and return to the starting point. This problem was originally posed by the Swiss mathematician Leonhard Euler in 1736 and played a significant role in the development of graph theory.
To solve this problem, we can represent the bridges and islands as a graph. Each island is represented as a vertex, and each bridge is represented as an edge connecting two vertices. By analyzing the connectivity and degree of the vertices in the graph, we can determine whether a solution exists.
In the given map, we would analyze the graph formed by the bridges and islands. If each island has an even degree (an even number of bridges connected to it), then it is possible to find a path that crosses each bridge exactly once and returns to the starting point. This can be proved using Euler's theorem, which states that in a connected graph, if the number of vertices with an odd degree is either 0 or 2, then there exists an Eulerian path or an Eulerian circuit respectively. However, if any island has an odd degree, it is not possible to find a path that satisfies the conditions of crossing each bridge exactly once and returning to the starting point.
Without further information or a specific map, it is not possible to determine the exact solution to exercise 10(b) in Chapter 10, Section 5. The solution would require analyzing the connectivity and degree of the bridges and islands in the given map and applying graph theory principles to determine the possibility of crossing all the bridges exactly once and returning to the starting point.
Learn more about vertex here:- brainly.com/question/32432204
#SPJ11
Match the graph with its equation
Answers
PLS ANSWER I DONT GET IT WILL GIVE BRAINLIEST :)!!! TYSM

Answers
what statistics are robust to outliers
Answers
There are several statistics that are robust to outliers: Median, Interquartile range, Winsorized mean and Trimmed mean.
How we find that what statistics are robust to outliers?These statistics are more suitable for datasets that contain outliers as they are less influenced by the extreme values and provide more accurate information about the central tendency and variability of the data.
Median: The median is less sensitive to extreme values in a dataset as it only considers the middle value, regardless of how large or small the other values are.Interquartile range (IQR): IQR is the difference between the third quartile (75th percentile) and the first quartile (25th percentile) of a dataset. It is calculated using the middle 50% of the data and is not influenced by the extreme values.Winsorized mean: The Winsorized mean is calculated by first replacing a fixed percentage (for example, 5%) of the largest and smallest values in a dataset with the nearest remaining value, and then calculating the mean. This method reduces the impact of extreme values on the mean.Trimmed mean: The trimmed mean involves removing a fixed percentage of the smallest and largest values in a dataset and then calculating the mean of the remaining values. This approach is similar to the Winsorized mean and also reduces the influence of extreme values on the mean.Learn more about Statistics are robust to outliers
brainly.com/question/28589666
#SPJ11
factor completely
8y²+6y+1
Answers
(4y + 1)(2y +1) this should be the answer: How to solve your problem
8
2
+
6
+
1
8
y
2
+
6
y
+
1
Grouping
1
Use the sum-product pattern
8
2
+
6
+
1
8
y
2
+
6
y
+
1
8
2
+
4
+
2
+
1
8
y
2
+
4
y
+
2
y
+
1
2
Common factor from the two pairs
8
2
+
4
+
2
+
1
8
y
2
+
4
y
+
2
y
+
1
4
(
2
+
1
)
+
2
+
1
4
y
(
2
y
+
1
)
+
2
y
+
1
3
Rewrite in factored form
4
(
2
+
1
)
+
2
+
1
4
y
(
2
y
+
1
)
+
2
y
+
1
(
4
+
1
)
(
2
+
1
)
(
4
y
+
1
)
(
2
y
+
1
)
Solution
(
4
+
1
)
(
2
+
1
)
During the period from 2011 through 2015 the annual returns on small U.S. stocks were - 3.80 percent, 19.15 percent, 45.91 percent, 3.26 percent, and - 3.80 percent, respectively. What would a $1 investment, made at the beginning of 2011 , have been worth at the end of 2015 ? (Round answer to 3 decimol places, eg. 52.750.) Value in 2015$ What average annual return would have been earned on this investment? (Round answer to 2 decimai ploces, eg. 52.75) Average annual return percent per year:
Answers
The average annual return on this investment from 2011 to 2015 is approximately 0.8%.
To calculate the value of a $1 investment made at the beginning of 2011 and its average annual return by the end of 2015, we need to multiply the successive annual returns and calculate the cumulative value.
The successive annual returns on small U.S. stocks from 2011 to 2015 are:
-3.80%, 19.15%, 45.91%, 3.26%, and -3.80%.
To calculate the cumulative value, we multiply the successive returns by the initial investment value of $1:
(1 + (-3.80%/100)) * (1 + (19.15%/100)) * (1 + (45.91%/100)) * (1 + (3.26%/100)) * (1 + (-3.80%/100))
Calculating this expression, we find that the cumulative value is approximately $1.044, rounded to three decimal places.
Therefore, a $1 investment made at the beginning of 2011 would have been worth approximately $1.044 at the end of 2015.
To calculate the average annual return, we need to find the geometric mean of the annual returns. We can use the following formula:
Average annual return = (Cumulative value)^(1/number of years) - 1
In this case, the number of years is 5 (from 2011 to 2015).
Average annual return = (1.044)^(1/5) - 1
Calculating this expression, we find that the average annual return is approximately 0.008 or 0.8% per year, rounded to two decimal places.
Therefore, the average annual return on this investment from 2011 to 2015 is approximately 0.8%.
Learn more about compound interest here:
https://brainly.com/question/24274034
#SPJ11
Find the equation of clean pulsations for a
left-mounted beam (for x=0) and simple pressed on the right (for
x=l) Take into account that: (sinx)^2+(cosx)^2=1
(chx)^2-(shx)^2=1
Answers
We can conclude that there are no nontrivial clean pulsations for the given left-mounted beam with a simple support on the right.
To find the equation of clean pulsations for a left-mounted beam with a simple support on the right, we can use the differential equation that describes the deflection of the beam. Assuming the beam is subject to a distributed load and has certain boundary conditions, the equation governing the deflection can be written as:
d^2y/dx^2 + (chx)^2 * y = 0
Where:
y(x) is the deflection of the beam at position x,
d^2y/dx^2 is the second derivative of y with respect to x,
ch(x) is the hyperbolic cosine function.
To solve this differential equation, we can assume a solution in the form of y(x) = A * cosh(kx) + B * sinh(kx), where A and B are constants, and k is a constant to be determined.
Substituting this assumed solution into the differential equation, we get:
k^2 * (A * cosh(kx) + B * sinh(kx)) + (chx)^2 * (A * cosh(kx) + B * sinh(kx)) = 0
Simplifying the equation and applying the given identity (chx)^2 - (shx)^2 = 1, we have:
(A + A * chx^2) * cosh(kx) + (B + B * chx^2) * sinh(kx) = 0
For this equation to hold for all values of x, the coefficients of cosh(kx) and sinh(kx) must be zero. Therefore, we get the following equations:
A + A * chx^2 = 0
B + B * chx^2 = 0
Simplifying these equations, we have:
A * (1 + chx^2) = 0
B * (1 + chx^2) = 0
Since we are looking for nontrivial solutions (A and B not equal to zero), the expressions in parentheses must be zero:
1 + chx^2 = 0
Using the identity (sinx)^2 + (cosx)^2 = 1, we can rewrite this equation as:
1 + (1 - (sinx)^2) = 0
Simplifying further, we get:
2 - (sinx)^2 = 0
Solving for (sinx)^2, we find:
(sin x)^2 = 2
Since the square of the sine function cannot be negative, there are no real solutions to this equation. Therefore, we can conclude that there are no nontrivial clean pulsations for the given left-mounted beam with a simple support on the right.
Learn more about simple support from
https://brainly.com/question/31510469
#SPJ11
Please help me solve the question

Answers
Answer:
Distributive propertyHope that helps! :)
-Aphrodite
Step-by-step explanation:
Answer:
D)
hope this helped
Step-by-step explanation:
5
Find the missing length.
7
C
c = √√√ [?]
C
Pythagorean Theorem: a2 + b2 = c²
Enter
Answers
The value of c in the right triangle using Pythagoras theorem is c = √113.
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
Pythagoras theorem shows the relationship between the sides of a right triangle. Hence:
c² = 8² + 7²
c = √113
The value of c in the right triangle using Pythagoras theorem is c = √113.
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
![5Find the missing length.7Cc = [?]CPythagorean Theorem: a2 + b2 = cEnter](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/0ZN2shLGdwsqQe2a7Ai6IDdesD6K1IJf.jpeg)
Use the image to find the area and the permiter

Answers
Answer:
Area = 45 units²
Perimeter = 29.4 units
Step-by-step explanation:
We can find the area of the shape in two parts.
The first part is the rectangle,
The area of the rectangle is calculated with the following formula:w × l
w: width, l: length7 × 5 = 35 units²
The second part is the triangle,
The area of the triangle is calculated with the following formula:\( \frac{1}{2} \times b \times h\)
b: base, h: height\( \frac{1}{2} \times 5 \times 4 = 10 \: \: {units}^{2} \)
To find the area of the whole shape, add both parts up:
35 units² + 10 units² = 45 units²
Now to find the perimeter of the whole shape, we simply add all side lengths' measures.9 + 7 + 5 + 2 + 6.4 = 29.4 units

Suppose the supply and demand equations for a product are given by: p²+4q = 253 183 p² + 6q0 - Find the equilibrium point, and enter it as a point. Equilibrium Quantity: q = Equilibrium Price: p =
Answers
The equilibrium point for the supply and demand equations p² + 4q = 253 and 183p² + 6q = 0 is (q, p) = (3, 10).
To find the equilibrium point, we need to solve the system of equations formed by the supply and demand equations. By substituting the value of q = 3 into the first equation, we get p² + 4(3) = 253, which simplifies to p² + 12 = 253.
Solving this equation gives us p = 10. Substituting the values of q = 3 and p = 10 into the second equation, we get 183(10)² + 6(3) = 0, which simplifies to 18300 + 18 = 0.
Since this equation holds true, we have found the equilibrium point to be (q, p) = (3, 10), where the equilibrium quantity is q = 3 and the equilibrium price is p = 10.
Learn more about Equation click here :brainly.com/question/13763238
#SPJ11
Polygon i a caled copy of Polygon. 2 4-ided polygon, P and Q. 1 ide in polygon P i 4 and it correponding ide in Q i 3. Another ide in polygon P i x, and it correponding ide in Q i y. The value of i 6, what i the value of ?
What i the cale factor?
Answers
When a side in polygon P is 6 the corresponding side in polygon Q is 4.5
the scale factor is 4/3
How to find the corresponding side of a scaled polygonFrom the question it can be deduced that
The polygon is four sided
1 side in polygon P is 4 and it corresponding side in Q is 3
let the scale factor be k
4 * k = 3
k = 3/4
When a side in polygon P is 6 the corresponding side in polygon Q is solved using the scale factor
the side in polygon Q = 6 * k
the side in polygon Q = 6 * 3/4
the side in polygon Q = 4.5
complete question
Polygon P is a scaled copy of Polygon Q. the 2 are 4-sided polygon, P and Q. 1 side in polygon P is 4 and it's correponding side in Q is 3. Another side in polygon P is x, and it correponding side in Q is y. The value of x is 6, what is the value of y?
What is the scale factor?
Learn more about scale factor:
https://brainly.com/question/26855848
#SPJ1
I need to find the derivative. I’m not very good at this so I am answer asap would be sosososo helpful

Answers
Answer:
See below.
Step-by-step explanation:
First, notice that this is a composition of functions. For instance, let's let \(f(x)=\sqrt{x}\) and \(g(x)=7x^2+4x+1\). Then, the given equation is essentially \(f(g(x))=\sqrt{7x^2+4x+1}\). Thus, we can use the chain rule.
Recall the chain rule: \(\frac{d}{dx}[f(g(x))]=f'(g(x))\cdot g'(x)\). So, let's find the derivative of each function:
\(f(x)=\sqrt{x}=x^\frac{1}{2}\)
We can use the Power Rule here:
\(f'(x)=(x^\frac{1}{2})'=\frac{1}{2}(x^{-\frac{1}{2} })=\frac{1}{2\sqrt{x}}\)
Now:
\(g(x)=7x^2+4x+1\)
Again, use the Power Rule and Sum Rule
\(g'(x)=(7x^2+4x+1)'=(7x^2)'+(4x)'+(1)'=14x+4\)
Now, we can put them together:
\(y'=f'(g(x))\cdot g'(x)=\frac{1}{2\sqrt{g(x)}} \cdot (14x+4)\)
\(y'=\frac{14x+4}{2\sqrt{7x^2+4x+1} } =\frac{7x+2}{\sqrt{7x^2+4x+1} }\)
2 + 7c – 4c2 – 3c + 4
Answers
Answer:-4c^2+4c+6
Step-by-step explanation:
Hope that’s what ur looking for:)
Answer:
2 + 7c – 4c2 – 3c + 4
4c∧2 + 4c + 6
Step-by-step explanation:
if a = -1/2 is a root of the quadratic equation 8x²-bx-3 . find the value of b, the other root, and (1/a - 1/b)²
Answers
Answer:
If a = -1/2 is a root of the quadratic equation 8x² - bx - 3, then we know that when x = -1/2, the equation is equal to 0. We can use this information to solve for b.
Substituting x = -1/2 into the equation, we get:
8(-1/2)² - b(-1/2) - 3 = 0
Simplifying and solving for b, we get:
2 - (b/2) - 3 = 0
b/2 = -1
b = -2
Therefore, b = -2 is the value we are looking for.
To find the other root, we can use the fact that the product of the roots of a quadratic equation is equal to the constant term divided by the leading coefficient. In this case, the constant term is -3 and the leading coefficient is 8. Therefore, the product of the roots is:
(-1/2) times the other root = -3/8
Solving for the other root, we get:
(-1/2) times the other root = -3/8
other root = (-3/8) / (-1/2)
other root = (3/8) * 2
other root = 3/4
Therefore, the other root is 3/4.
Finally, to find (1/a - 1/b)², we can substitute a = -1/2 and b = -2 into the expression:
(1/a - 1/b)² = (1/(-1/2) - 1/(-2))²
= (-2 - 1/2)²
= (-5/2)²
= 25/4
Therefore, (1/a - 1/b)² is equal to 25/4.
Answer:
\(b=2\)
\(\textsf{Other root} = \dfrac{3}{4}\)
\(\left(\dfrac{1}{a}-\dfrac{1}{b}\right)^2=\dfrac{25}{4}\)
Step-by-step explanation:
Roots are also called x-intercepts or zeros. They are the x-values of the points at which the function crosses the x-axis, so the values of x when f(x) = 0.
If x = α is a root of a polynomial f(x), then f(α) = 0.
Therefore, given that a = -1/2 is a root of the quadratic equation 8x² - bx - 3, substitute x = -1/2 into the equation and set it to zero:
\(\implies 8\left(-\dfrac{1}{2}\right)^2-b\left(-\dfrac{1}{2}\right)-3=0\)
Solve for b:
\(\implies 8\left(\dfrac{1}{4}\right)+\dfrac{1}{2}b-3=0\)
\(\implies \dfrac{8}{4}+\dfrac{1}{2}b-3=0\)
\(\implies 2+\dfrac{1}{2}b-3=0\)
\(\implies \dfrac{1}{2}b-1=0\)
\(\implies \dfrac{1}{2}b=1\)
\(\implies b=2\)
Therefore, the quadratic equation is:
\(\boxed{8x^2-2x-3}\)
The product of the roots of a quadratic equation is equal to the constant term divided by the leading coefficient.
The constant term of the quadratic equation is -3 and the leading coefficient is 8. Let the other root be "r". Therefore:
\(\implies a \cdot r=\dfrac{-3}{8}\)
Substitute the known value of a = -1/2 and solve for r:
\(\implies -\dfrac{1}{2} \cdot r=\dfrac{-3}{8}\)
\(\implies r=\dfrac{3}{4}\)
Therefore, the other root of the quadratic equation is 3/4.
To find the value of (1/a - 1/b)², substitute the given value of a and the found value of b into the equation and solve:
\(\implies \left(\dfrac{1}{a}-\dfrac{1}{b}\right)^2\)
\(\implies \left(\dfrac{1}{-\frac{1}{2}}-\dfrac{1}{2}\right)^2\)
\(\implies \left(-2-\dfrac{1}{2}\right)^2\)
\(\implies \left(-\dfrac{5}{2}\right)^2\)
\(\implies \dfrac{25}{4}\)
holly drinks 2 2/5 litre of water each day. The water comes in 1 2/5 litre bottles. How many bottles does Holly drink in a week?
Answers
Answer:Holly drank 12 bottles in a week.
Step-by-step explanation:
First change the fraction 1 2/5 litre into a decimal, by doing this, we can know how many litres are there in 2/5.
So= 1 2/5
= 2 ÷5 = 0.4
= 1 + 0.4 = 1.4 liters
1.4 liters is the amount of water in a bottle.
Next, also change the fraction 2 2/5 litres into a decimal.
So=2 2/5
= 2÷5 = 0.4
= 2 + 0.4 = 2.4 liters
She drinks 2.4 liters a day.
To find how many bottles she drank in 1 week, we must multiply the amount of water she drinks in a day to the days in a week.
So= 1 week= 7 days
= 1 day= 2.4 liters
So= 2.4 × 7 = 16.8
She drinks 16.8 in a week.
To find how much bottles she drank in a week, we must divide the amount of liters she drank in one week to the amount of liters are there in a bottle.
So= 16.8 ÷ 1.4= 12 bottles
Holly drinks 12 bottles in a week.
I hope this helps! I'm sorry if it's wrong and complicated.
Solve using the quadratic formula

Answers
By using the quadratic formula, the solution to this quadratic equation is equal to -0.5251 or -3.8081.
What is a quadratic equation?In Mathematics, a quadratic equation can be defined as a mathematical expression that can be used to define and represent the relationship that exists between two or more variable on a graph. In Mathematics, the standard form of a quadratic equation is given by;
ax² + bx + c = 0
Mathematically, the quadratic formula is modeled or represented by this mathematical expression:
\(x = \frac{-b\; \pm \;\sqrt{b^2 - 4ac}}{2a}\)
From the information provided, we have the following values;
3x² + 13x + 4 = 0
Where:
a = 3
b = 13
c = 4
Substituting the values into the quadratic formula, we have the following;
\(x = \frac{-(13)\; \pm \;\sqrt{(13)^2 - 4(3)(13)}}{2(3)}\\\\x = \frac{-13\; \pm \;\sqrt{169 - 72}}{6}\)
x = (-13 + √97)/6
x = -0.5251 or -3.8081.
Read more on quadratic equation here: https://brainly.com/question/4053652
#SPJ1
solve the equation: sin(2x)= sin x
Answers
Answer:
Below
Step-by-step explanation:
sin(2x) = 2 ×cos(x)× sin(x)
● sin(x) = 2 × cos(x) × sin(x)
● 2 × cos(x) = 1
● cos (x) = 1/2
So we can deduce that:
● x = Pi/3 + 2*k*Pi
● or x = -Pi/3 + 2*k*Pi
K is an integer
The Solution of x:
x = π/3 + 2πn, where n is an integer.
x = 2π/3 + 2πn, where n is an integer.
In degrees:
x = 60° + 360°n, where n is an integer.
x = 120° + 360°n, where n is an integer.
To solve the equation sin(2x) = sin(x), we can use the properties of trigonometric functions.
First, let's simplify the equation using the double angle identity for sine:
sin(2x) = 2sin(x)cos(x).
Now we can rewrite the equation as:
2sin(x)cos(x) = sin(x).
2cos(x) = 1.
Dividing both sides of the equation by cos(x), we get:
2 = 1/cos(x).
Now, we can find the value of cos(x) by taking the reciprocal of both sides:
cos(x) = 1/2.
From the unit circle or trigonometric values,
we know that cos(x) = 1/2 corresponds to angles of π/3 or 2π/3 (in radians) or 60° or 120° .
So, the solutions for x are:
x = π/3 + 2πn, where n is an integer.
or
x = 2π/3 + 2πn, where n is an integer.
In degrees:
x = 60° + 360°n, where n is an integer.
or
x = 120° + 360°n, where n is an integer.
Learn more about Trigonometry here:
https://brainly.com/question/13262593
#SPJ6