3(4x +2) +3
I need help!!
Thx!
Answers
Answer:
12x+9
Hope you got your answer!
Related Questions
1. A company produces two types of nutritional supplements; Energize and Excel. Energize contains 26 mg of vitamin A, 42 mg of vitamin C and 25 mg of an herbal supplement. Excel contains 68 mg of vitamin A, 61 mg of vitamin C and 15 mg of the herbal supplement. An athlete is told that he needs at least 489 mg of vitamin A, 1130 mg of vitamin C and 348 mg of the herbal supplement for optimal athletic performance. The athlete wants to take the supplements, but at the lowest possible cost. Energize pills cost 40 cents each, while Excel pills cost 100 cents each. Let x = the number of Energize pills to take, and let y = the number of Excel pills to take. Which of the following is the objective function for this situation?
A) Minimize C = 40x + 100y.
B) Maximize C = 40x + 100y.
C) Minimize C = 11300x + 3480y.
D) Maximize C = 100x + 40y.
E) Minimize C = 100x + 40y.
F) None of the above.
2. A company produces two types of bicycles; mountain bikes and racing bikes. It takes 7 hours of assembly time and 5 hours of mechanical tuning to produce a mountain bike. It takes 8 hours of assembly time and 4 hours of mechanical tuning to produce a racing bike. The company has at most 22 hours of mechanical tuning labor per week and at most 190 hours of assembly labor per week. The company's profit is $50 for each mountain bike produced and $130 for each racing bike produced. The company wants to make as much money as possible. Let x = the number of mountain bikes they produce, and let y = the number of racing bikes they produce. What are the constraints for this problem?
a) 7x + 5y ≤ 190, 8x + 4y ≤ 22, x ≥ 0, y ≥ 0.
b) 7x + 8y ≥ 190, 5x + 4y ≤ 22, x ≥ 0, y ≥ 0.
c) 5x + 8y ≤ 190, 7x + 4y ≤ 22, x ≥ 0, y ≥ 0.
d) 7x + 8y ≤ 190, 5x + 4y ≤ 22, x ≥ 0, y ≥ 0.
e) 7x + 8y ≤ 190, 5x + 4y ≥ 22, x ≥ 0, y ≥ 0.
f) none of the above.
3. A certain academic department at a local university will conduct a research project. The department will need to hire graduate research assistants and professional researchers. Each graduate research assistant will need to work 23 hours per week on fieldwork and 17 hours per week at the university's research center. Each professional researcher will need to work 15 hours per week on fieldwork and 25 hours per week at the university's research center. The minimum number of hours needed per week for fieldwork is 154 and the minimum number of hours needed per week at the research center is 140. Each research assistant will be paid $295 per week and each professional researcher will be paid $416 per week. Let xdenote the number of graduate research assistants hired and let y denote the number of professional researcher hired. The department wants to minimize cost. Set up the Linear Programming Problem for this situation.
A) Min C = 416x + 295y; s.t 23x + 17y ≥ 154, 15x + 25y ≥ 140, x ≥ 0, y ≥ 0.
B) Min C = 295x + 416y; s.t 23x + 15y ≥ 154, 17x + 25y ≥ 140, x ≥ 0, y ≥ 0.
C) Min C = 295x + 416y; s.t 23x + 15y ≥ 154, 25x + 17y ≥ 140, x ≥ 0, y ≥ 0.
D) Min C = 295x + 416y; s.t 15x + 23y ≤ 140, 25x + 17y ≤ 154, x ≥ 0, y ≥ 0.
E) Min C = 416x + 295y; s.t 15x + 23y ≥ 154, 25x + 17y ≥ 140, x ≥ 0, y ≥ 0.
F) None of the above.
Answers
Answer:
1)A) Minimize C = 40x + 100y.
2) d) 7x + 8y ≤ 190, 5x + 4y ≤ 22, x ≥ 0, y ≥ 0.
3) B) Min C = 295x + 416y; s.t 23x + 15y ≥ 154, 17x + 25y ≥ 140, x ≥ 0, y ≥ 0.
Step-by-step explanation:
1) Energize pills cost 40 cents each, while Excel pills cost 100 cents each. If x represent the energize pills and y represent the excel pills, the objective function would be:
minimize cost = cost of energize pill + cost of excel pill
Minimize cost = 40x + 100y
2) Let x = the number of mountain bikes they produce, and let y = the number of racing bikes they produce.
7 hours of assemble time to produce a mountain bike and 8 hours of assemble time to produce a racing bike. Since the company has at most 190 hours for assemble time, it can be represented as:
7x + 8y≤ 190
5 hours of mechanical tuning to produce a mountain bike and 4 hours of mechanical tuning to produce a racing bike. Since the company has at most 22 hours for mechanical tuning, it can be represented as:
5x + 4y ≤ 22
Also assemble time and mechanical time must be greater than 0, hence:
x ≥ 0, y ≥ 0
3) The fieldwork constraint can be represented as:
23x + 15y ≥ 154
The time to be spent at university research center can be represented as:
17x + 25y ≥ 140
Both fieldwork time and time spent at university research center mut be greater than 0, hence:
x ≥ 0, y≥ 0
The cost equation is:
Minimize cost = 295x + 416y
If 11 boxes of chocolates contain 220 chocolates in total, calculate how many chocolates 5 box of chocolates will contain
chocolates
Answers
Answer:100 chocolates
Step-by-step explanation:
20 chocolate in each box so 20 time 5 is 100 so 20 time 11 is 220
I NEED HELP PLEASE, THANKSSS! :)

Answers
Answer: A) max at (14, 6) = 64, min at (0,0) = 0
Step-by-step explanation:
Graph the lines at look for the points of intersection.
Input those points into the Constraint function (2x + 6y) and look for the maximum value and minimum value.
Points of Intersection: (0, 0), (17, 0), (0, 10), (14, 6)
Point Constraint 2x + 6y
(0, 0): 2(0) + 6(0) = 0 Minimum
(17, 0): 2(17) + 6(0) = 34
(0, 10): 2(0) + 6(10) = 60
(14, 6): 2(14) + 6(6) = 64 Maximum

100 POINTS HELPPPP What entry on a cash flow statement would indicate that a business had a cash inflow from the sale of equipment?
A. Negative CapEx
C. Negative repayment of debt
B. Inflow from sale of PPE
D. Positive issuance of equity
Answers
Answer:
The cash flow statement paints a picture as to how a company’s operations are running, where its money comes from, and how money is being spent. So i think D is the answer
g. Use a spreadsheet to solve the absolute value equations in part (f).
Explain your method.
123456
7
8
9
10
11
A
X
-8
-7
-6
-5
-4
-3
-2
-1
0
B
|x + 21
6
=abs(A2 + 2)
Pls help omg

Answers
Starting from the x-value (A column) for -7 and going down the y-values values (B column) are 5, 4, 3, 2, 1, 0, 1, 2
Step-by-step explanation:The function is given to us in the B column. We can use this to find the y-values without having to plug them in each time.
Finding the Vertex
In absolute value functions, there is a vertex. The vertex, in this case, is the minimum where the y-values change from decreasing to increasing. The absolute value formula is y = a|x - h| + k.
The vertex is equal to (h,k). The h-value in the function above is -2 and the k-value is 0. Thus, the vertex is at (-2,0).
Finding Slope
The slope of an absolute value function is written before the x. Since there isn't anything before the x in this function, the slope must be 1. So, the values either increase or decrease by 1.
Like all positive absolute value functions, the graph will decrease, reach 0, then begin to increase. The graph will reach 0 at the vertex.
Writing Out the Values
The table shows us that the y-values begin at 6. Then, we decrease by one until we get to 0.
So, the first values are 6, 5, 4, 3, 2, 1, 0Each of these x-values matches up with one of the y-values. Then, the graph begins to increase once again.
The next values are 1 and 2So together the y-values for the x-values -8 through 0 are 6, 5, 4, 3, 2, 1, 0, 1, 2.
Can someone please help me with this I don’t get it
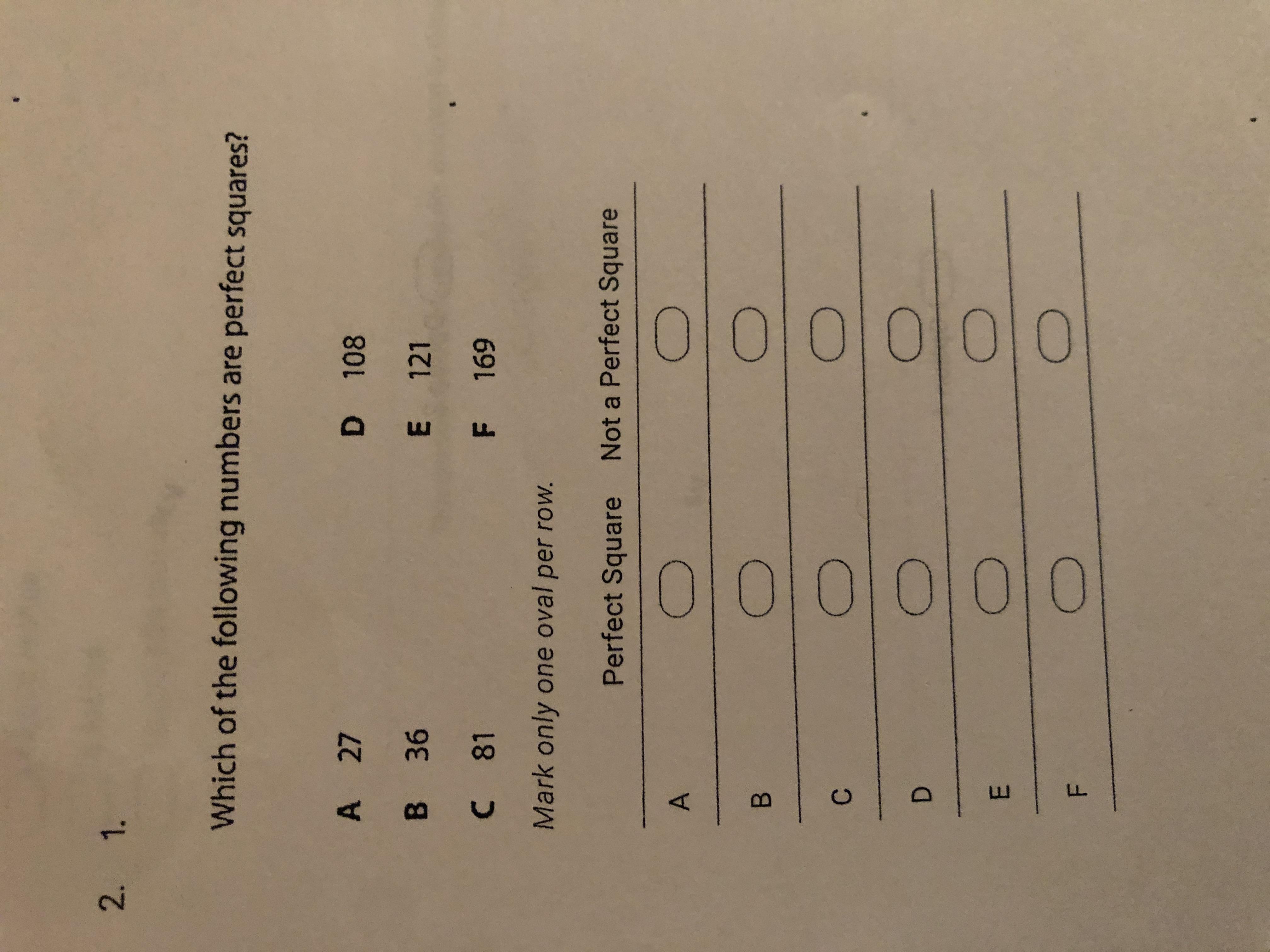
Answers
Answer:
b,c,e,f is perfect square and other are not a perfect square
Answer: i'll show you how to do it.
Step-by-step explanation:
Is there any number that multiplied by itself gives you one of the options obove?
Example:
81 = 9×9... So it is a perfect square
36 = 6x6... It's a perfect square too
27 = ther isn't a number that multipied by itself is equal to 27... Then, it is not a perfect square
a + (-7) = 3 a =
1.9 + b = -3.2 b =
-1/6 +7/6 = c c=
Answers
The value of the equations are a = 10 , b = -5.1 and c = 1
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be represented as A
Now , the value of A is
Substituting the values in the equation , we get
a + ( -7 ) = 3 be equation (1)
On simplifying the equation , we get
a - 7 = 3
Adding 7 on both sides of the equation , we get
a = 3 + 7
a = 10
Substituting the values in the equation , we get
1.9 + b = -3.2 be equation (2)
Subtracting 1.9 on both sides of the equation , we get
b = -3.2 - 1.9
b = -5.1
Substituting the values in the equation , we get
-1/6 + ( 7/6 ) = c be equation (3)
c = ( 7 - 1 ) / 6
c = 6/6
c = 1
Hence , the equations are solved
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
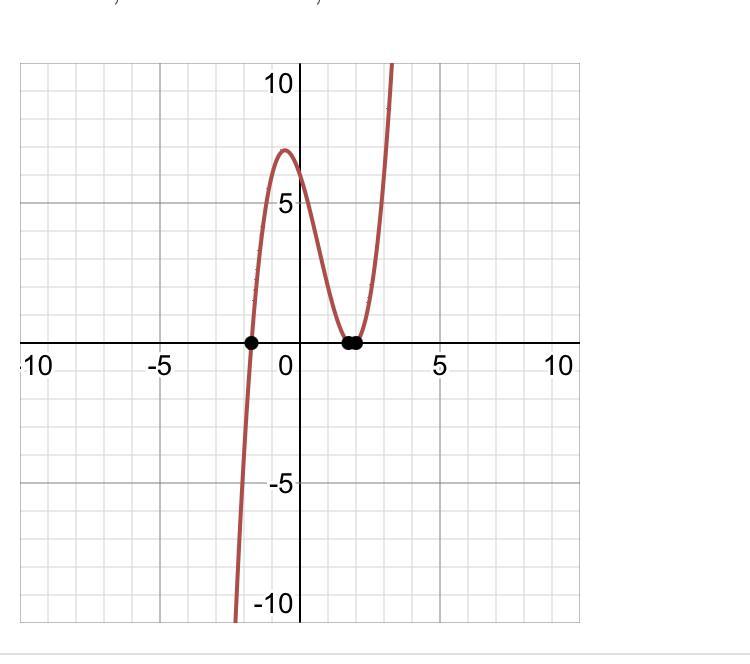
x² + 2x²-3x-6
Get the zeros
Answers
y
=
x
3
−
2
x
2
−
3
x
+
6
y
=
x
3
-
2
x
2
-
3
x
+
6
To find the roots of the equation, replace
y
y
with
0
0
and solve.
0
=
x
3
−
2
x
2
−
3
x
+
6
0
=
x
3
-
2
x
2
-
3
x
+
6
Replace
y
y
with
0
0
and solve for
x
x
.
Tap for more steps...
x
=
2
,
√
3
,
−
√
3
x
=
2
,
3
,
-
3
The result can be shown in multiple forms.
Exact Form:
x
=
2
,
√
3
,
−
√
3
x
=
2
,
3
,
-
3
Decimal Form:
x
=
2
,
1.73205080
…
,
−
1.73205080
…
Answer:
3x^2-3x-6=3(x^2-x-2)=3(x-2)(x+1)
x=2/x=-1
Step-by-step explanation:
For the function f(x)=x+4−−−−−√
, the average rate of change to the nearest hundredth over the interval 2 ≤ x ≤ 6 is
Answers
The average rate of change of the function f(x) = √(x+4) over the interval 2 ≤ x ≤ 6 is approximately 0.29 to the nearest hundredth.
To find the average rate of change of the function f(x) = √(x+4) over the interval 2 ≤ x ≤ 6, we need to calculate the change in the function divided by the change in the input variable over that interval.
The change in the function between x = 2 and x = 6 is:
f(6) - f(2) = √(6+4) - √(2+4) = √10 - √6
The change in the input variable between x = 2 and x = 6 is:
6 - 2 = 4
So, the average rate of change of the function over the interval 2 ≤ x ≤ 6 is:
(√10 - √6) / 4
To approximate the answer to the nearest hundredth, we can use a calculator or perform long division to get:
(√10 - √6) / 4 ≈ 0.29
For such more questions on function
https://brainly.com/question/11624077
#SPJ8
Makayla's math teacher plots student grades on their weekly quizzes
against the number of hours they say they study on the pair of
coordinate axes and then draws the line of best fit. What is the
meaning of the x-value on the line when y = 100?
95
90
85
80
75
t
8
70
65
60
55
50
Quiz Score
100
45
O
0.5 1
O
1.5 2
O
O
00
00
oo
2.5 3 3.5 4 4.5 5 5.5 6
Time Spent on Homework per Week (hours)
A student's expected quiz score if they spent 100 hours on their
homework.
The number of hours a student should spend on their
homework to expect a score of 100 on the quiz.
The number of hours a student actually spent on homework
before earning a score of 100 on the quiz.
A student's actual quiz score after spending 100 hours on their
homework.
Answers
The meaning of the x-value on the line when y = 100 is the number of hours a student should spend on their homework to expect a score of 100 on the quiz.
1. The given information suggests that the math teacher plots student grades on the y-axis (vertical axis) and the number of hours they study on the x-axis (horizontal axis).
2. The teacher then draws a line of best fit, which represents the general trend or relationship between the quiz scores and the number of study hours.
3. We are asked to determine the meaning of the x-value on the line when y = 100, which implies finding the number of study hours required to expect a score of 100 on the quiz.
4. To find this value, we look for the point on the line where the y-coordinate is 100.
5. By observing the graph or equation of the line, we can determine the corresponding x-value or the number of study hours.
6. In this case, the x-value corresponding to y = 100 represents the number of hours a student should spend on their homework to expect a score of 100 on the quiz.
7. Therefore, the x-value on the line when y = 100 provides an estimate of the amount of time a student needs to allocate for studying in order to achieve a score of 100 on the quiz.
For more such questions on x-value, click on:
https://brainly.com/question/30665072
#SPJ8
How many schools have fewer than 50 classrooms

Answers
Answer:
7 schools have fewer than 50 classrooms.
3.16 Summer Temperatures L.A. and NYC The histograms below were created from data on the daily high temperature in Los Angeles and New York City during a summer month. Compare the two distributions. Which city do you think has the higher typical temperature? Which city has more variation in temperature? Explain. (Source: Accuweather.com) 0.5 0.5 - 0.4 0.4 0.3 0.3 Relative Frequency Relative Frequency 0.2 0.2 0.1 0.1 65 70 0 65 75 85 90 95 70 75 85 90 95 80 L.A. 80 NYC
Answers
Based on the histograms, it appears that Los Angeles has a higher typical temperature than New York City during the summer month.
What is distribution?In statistics, a distribution is a way of showing how data is spread out or arranged. It describes the pattern of values in a dataset, and provides information on the frequency, range, and possible values of the data.
A distribution can take many forms, depending on the type of data being analyzed. For example, a distribution can be:
Symmetrical: where the data is evenly distributed around a central value, such as a normal distribution.
Skewed: where the data is not evenly distributed and is clustered more towards one end of the range than the other end, such as a positively skewed distribution.
Bimodal: where there are two distinct peaks in the data, such as in a distribution of test scores for a class with both high-performing and low-performing students.
There are many ways to represent a distribution, but some common methods include histograms, box plots, and probability density functions.
Understanding the distribution of data is important in statistics because it can help identify patterns, trends, and outliers in the data. It can also help inform decisions about which statistical methods to use when analyzing the data.
Here,
In the Los Angeles histogram, the peak of the distribution is around 80 degrees Fahrenheit, whereas in the New York City histogram, the peak is around 75 degrees Fahrenheit. However, the New York City histogram appears to have more variation in temperature than the Los Angeles histogram. This can be seen in the wider spread of the distribution, with a range of temperatures from around 65 to 95 degrees Fahrenheit, compared to the narrower range of temperatures in the Los Angeles distribution, which ranges from around 70 to 90 degrees Fahrenheit.
In other words, while the typical temperature in Los Angeles during the summer month is higher than in New York City, the temperature in New York City varies more widely from day to day.
To know more about distribution,
https://brainly.com/question/14503886
#SPJ1
What is the area of a sector when 0=pi/2 radians and r=8/3

Answers
\(\textit{area of a sector of a circle}\\\\ A=\cfrac{\theta r^2}{2} ~~ \begin{cases} r=radius\\ \theta =\stackrel{radians}{angle}\\[-0.5em] \hrulefill\\ \theta =\frac{\pi }{2}\\[1em] r=\frac{8}{3} \end{cases}\implies A=\cfrac{1}{2}\cdot \cfrac{\pi }{2}\cdot\left( \cfrac{8}{3} \right)^2 \\\\\\ A=\cfrac{1}{2}\cdot \cfrac{\pi }{2}\cdot \cfrac{64}{9}\implies A=\cfrac{16\pi }{9}\implies A\approx 5.59\)
An open-top box is to be made from a 12-inch by 24-inch piece of plastic by removing a square from each corner of the plastic and folding up the flaps on each side. What is the maximum possible volume, in cubic inches, of the box?
Answers
Answer:
The maximum possible volume = 332.685 cubic inches
Step-by-step explanation:
From the information given:
Let the height be = x
The length be = 24 - 2x
The width be = 12 - 2x
Then V = x (24 -2x) ( 12 - 2x)
V = x ( 288 -48x - 24x +4x²)
V = x(288 - 72x + 4x²)
V = 288x - 72x² + 4x³
\(\dfrac{dV}{dx}= (3x^2 - 36x+ 72)\)
\(\implies x^2 - 12x + 24 = 0\)
\(=\dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)
\(=\dfrac{-(-12) \pm \sqrt{(-12)^2 - 4(1)(24)}}{2(1)}\)
\(=\dfrac{12 \pm \sqrt{144 - 96}}{2}\)
\(=\dfrac{12 \pm \sqrt{48}}{2}\)
where;
\(x \ne \dfrac{12 + \sqrt{48}}{2}\)
∴ \(x= \dfrac{12 - \sqrt{48}}{2}\)
x = 2.536 ( since the length cannot be negative)
So, the length x = 24 - 2(2.535) = 18.93
The width = 12 - 2(2.535) = 6.93
heigth = 2.536
∴
V = 18.93 × 6.93 × 2.536
V = 332.685 cubic inches
A box is made from a plastic sheet by removing square from each corner, maximum volume of this box will be 332.55 cubic inches.
Volume of a cuboid: Volume of a cuboid or rectangular box is given by the expression,Volume = Length × Width × Height
Given in the question,
Plastic sheet with length = 12 inches Width of the sheet = 24 inches A square has been removed from each corner to fold the box.Let the measure of each side of a square removed = x inches
Therefore, length of the box = (12 - 2x) inches
Width of the box = (24 - 2x) inches
Height of the box = x inches
Volume of the box (V) = (12 - 2x) × (24 - 2x) × (x)
V = 4x³ - 72x² + 288x
To find the maximum volume of the box differentiate the expression with respect to 'x' and equate it to zero.
V' = 12x² - 144x + 288
For V' = 0,
12x² - 144x + 288 = 0
x² - 12x + 24 = 0
\(x=\frac{12\pm\sqrt{(12)^2-4(1)(24)} }{2(1)}\)
\(x=(6\pm2\sqrt{3})\)
\(x=9.46,2.54\)
For x = 9.46,
Volume of the box = 4(9.46)³- 72(9.46)² + 288
= -2769.03 cubic inches
For x = 2.54,
Volume of the box = 4(2.54)³- 72(2.54)² + 288
= 332.55 cubic inches
Therefore, maximum volume of the box will be 332.55 cubic inches.
Learn more about the volume of a cuboid here,
https://brainly.com/question/25395659?referrer=searchResults

A man's gross income is R500 000. He worked at different places throughout the year
and a total of 17% of his earnings was deducted by his employers as PAYE throughout
the tax year. He qualifies for a rebate of R13 257. Calculate how much tax he still
owes. Information taken from the tax table shows that, for a taxable income between
R393 201 and R550 100, R93 135 + 36% above R393 200 needs to be paid.
O R101 678
O R71 774
O R33 326
O R25 191
<
Previou
Next >
Answers
The man still owes R87,726 in taxes.
To calculate the tax amount the man still owes, we need to determine his taxable income first.
Gross income: R500,000
Less: PAYE deductions (17% of gross income): R500,000 * 0.17 = R85,000
Taxable income: R500,000 - R85,000 = R415,000
Next, we can use the tax table information provided to calculate the tax owed based on the taxable income.
Tax owed: R93,135 + 36% of (taxable income - R393,200)
Tax owed: R93,135 + 0.36 * (R415,000 - R393,200)
Tax owed: R93,135 + 0.36 * R21,800
Tax owed: R93,135 + R7,848
Tax owed: R100,983
Finally, we subtract the rebate amount of R13,257 from the tax owed to find the amount the man still owes.
Tax owed - Rebate: R100,983 - R13,257 = R87,726
Therefore, the man still owes R87,726 in taxes.
The correct option is not provided among the given answer choices.
for such more question on tax amount
https://brainly.com/question/16950901
#SPJ8
T what do you guys think of this (I know this is for help with math but I have no socail media.)

Answers
Answer:
This is very cute.
Step-by-step explanation:
Answer:
Cute
Step-by-step explanation:
The weights of four similar packs of tomatoes are listed below.
Pack A: 2.456 pounds
Pack B: 2.457 pounds
Pack C: 2.454 pounds
Pack D: 2.459 pounds
Malcolm rounds the weights to the nearest hundredth pound. Which weight does
not round to 2.46 pounds?
A 2.456 pounds
B 2.457 pounds
C 2.454 pounds
D 2.459 pounds
Answers
Answer:
The weight that does not round to 2.46 pounds is C 2.454 pounds.
Step-by-step explanation:
Based on the given information, the weights of the four similar packs of tomatoes are as follows:
Pack A: 2.456 poundsPack B: 2.457 poundsPack C: 2.454 poundsPack D: 2.459 poundsMalcolm rounds the weights to the nearest hundredth pound. To round to the nearest hundredth pound, we look at the digit in the hundredths place. If it is 5 or greater, we round up the digit in the tenths place. If it is less than 5, we leave the digit in the tenths place as it is. Therefore, we can obtain the rounded weights as follows:
Pack A: 2.46 poundsPack B: 2.46 poundsPack C: 2.45 poundsPack D: 2.46 poundsFrom the above rounded weights, we see that Pack C rounds to 2.45 pounds and does not round to 2.46 pounds. Therefore, the weight that does not round to 2.46 pounds is C 2.454 pounds.
Describe the meanings of all the variables in the exponential functionQ=Q0 (1+r) t Explain how the function is used for exponential growth and decay. Choose the correct answer below. Select all that apply. A. The function is used for exponential growth if r<0B. The function is used for exponential decay if r>0C. The function is used for exponential growth if r>0D. The function is used for exponential decay if r<0.
Answers
The exponential function Q=Q0 (1+r) t can be used to describe exponential growth or decay depending on the value of r. If r is less than 0, the function can be used to describe exponential growth, whereas if r is greater than 0, the function can be used to describe exponential decay.
The exponential function Q=Q0 (1+r) t can be used to describe exponential growth or decay. The function is determined by three variables: Q0, which is the starting value of the function; r, which is the growth or decay rate of the function; and t, which is the time when the function occurs. If r is less than 0, then the function can be used to describe exponential growth, meaning that the output of the function will increase over time. On the other hand, if r is greater than 0, then the function can be used to describe exponential decay, meaning that the output of the function will decrease over time. The exponential function can be used to describe a variety of different processes, such as population growth, compound interest, and radioactive decay. It can also be used to predict future values based on past values by using the growth or decay rate. Thus, the exponential function is a powerful tool for describing and predicting exponential growth and decay.
Q=Q0 (1+r) t
For example, if Q0 = 10, r = 0.5, and t = 5, then
Q=10 (1+0.5)5
Q= 10 x 1.53
Q= 15.3
Learn more about function here
https://brainly.com/question/29633660
#SPJ4
E-7/9|12/5-6R|+50 > or equal to -30
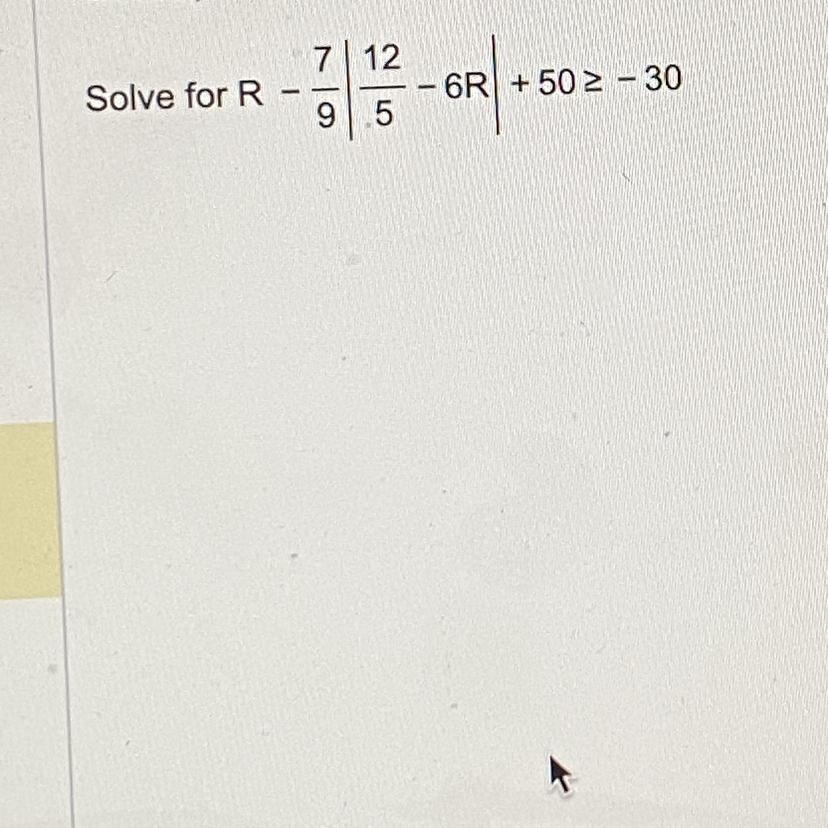
Answers
The solution set of the inequality for R is given by \(-\frac{1172}{85} \leq x\leq \frac{1228}{55}\) .
An inequality in mathematics is a relation that compares two numbers or other mathematical expressions in an unequal way. It is frequently used to compare two numbers on the number line based on their sizes. Different types of inequalities are represented by a variety of notations such as < ,> ,≤ and ≥.
The modulus function takes the absolute value of a function.
To solve the given inequality we have simplify the inequality first.
\(x-\frac{7}{9} |(\frac{12}{5} -6x)|+50\ge -30\)
\(or, x-\frac{7}{9}\times \frac{6}{5} |(2-5x)|+50\ge -30\\or,x-\frac{14}{15}|2-5x|\ge-80\\\)
Now we separate the inequalities:
\(x-\frac{14}{15}(2-5x)\ge-80\) for 2x-5 ≥ 0
\(x-\frac{14}{15}(-(2-5x))\ge-80\) for 2x-5 ≤ 0
Now we will solve the two inequalities separate and find the intersection.
\(x-\frac{14}{15}(2-5x)\ge-80\\or,15x-28+70x\ge-1200\\or,x\ge -\frac{1172}{85}\)
Again
2x-5 ≥ 0
or, \(x\le\frac{2}{5}\)
hence \(-\frac{1172}{85}\le x\le\frac{2}{5}\)
Similarly solving the other inequality we get
\(\frac{2}{5}\le x\le\frac{1228}{55}\)
Now we find the intersection of the two inequalities:
\(-\frac{1172}{85}\le x\le\frac{1228}{55}\)
To learn more about inequalities visit:
https://brainly.com/question/20383699
#SPJ9
Which expression represents 9
9
less than an unknown number?
Answers
Answer:
If we denote the unknown number as "x", then the expression representing "9 less than the unknown number" would be:
x - 9
Newton's Law of Cooling states that the rate of change of the temperature of an object, T, is proportional to the difference of T and the temperature of its surrounding environment. A pot of chili with temperature 23°C is placed into a −18°C freezer. After 2 hours, the temperature of the chili is 7°C.
Part A: Assuming the temperature T of the chili follows Newton's Law of Cooling, write a differential equation for T. (10 points)
Part B: What is the temperature of the chili after 4 hours? (20 points)
Part C: At what time, t, will the chili's temperature be −10°C? (10 points)

Answers
For this, let's go through each problem carefully and step-by-step.
According to the question, the rate of change of the temperature of any object that is defined by T, is directly proportional to the difference of T and the temperature of the environment around it, which we'll denote as X.
\(\frac{dT}{dt}\)\(= k (T-X)\)
K is a constant of proportionality here. And the temperature of the surrounding environment is said to be (-18°C). Thus,
\(\frac{dT}{dt} = k(T+18)\).
For part A, in order to find the differential equation for T, we need to solve for k. So we separate the variables and then integrate to solve the equation.
\(\int\limits{\frac{dT}{T+18} } = \int\limits {k} \, dt\)
\(ln(T+18) = kt+c\)
Now thw inital temperature of a pot of chili is 23°C, so at \(t = 0, T_0 = 23*C\).
Substituting 23 for T and 0 for t, we have the following:
\(ln(23+18) = k(0)+c\)
\(ln(41) = c\)
We know the temperature of chili after 2 hours is 7°C, so we know that when \(t = 2, T_1 = 7\)
Substituting t for 2, and T for 7, we get:
\(ln(7+18) = 2k+ln(41)\)
\(ln(25) = 2k + ln(41)\)
Solving for 2k
\(2k = ln(25) -ln(41)\)
\(2k = ln(\frac{25}{41})\)
\(k = \frac{1}{2}ln(\frac{25}{41})\).
Substituting the value of \(\frac{dT}{dt} = k (T+18)\), the differential equation obtained is \(\frac{dT}{dt} = \frac{1}{2}ln(\frac{25}{41})(T+18)\).
For part B, to find the temperature of the chili after four hours, we first need to solve the above differential equation.
The solution of the differential equation is given by the equation \(ln(T+18) = kt+c\). Substituting the values of k and c, we have:
\(ln(T+18) = \frac{1}{2}ln(\frac{25}{41})t+ln(41)\).
Using the above relation, at any time (t), the temperature (T) can be found out in the following.
At \(t = 4, T_2 = \phi\)
\(ln(T_2+18)=\frac{1}{2}ln(\frac{25}{41})*4+ln(41)\)
\(ln(T_2+18)=2ln(\frac{25}{41})+ln(41)\)
\(ln(T_2+18)=-0.989 + 3.714\)
\(ln(T_2+18)\) ≅ \(2.725\)
Solving the natural logarithm,
\(T_2+18 = e^{2.725} = 15.256\)
\(T_2 =15.256 - 18\)
\(T_2 = -2.744\).
So the temperature of the chili after four hours would be -2.744°C approximately.
To find part C in what time the chili would be 10°C, we need to substitute again.
\(t = \phi\)\(, T = -10\)
\(ln(-10 + 18) = \frac{1}{2}ln(\frac{25}{41})t + ln(41)\)
\(ln(8) = \frac{1}{2}ln(\frac{25}{41})t + ln(41)\)
Solving for \(\frac{1}{2}ln(\frac{25}{41})t\),
\(\frac{1}{2}ln(\frac{25}{41})t = ln(8) - ln(41)\)
\(\frac{1}{2}ln(\frac{25}{41})t = ln(\frac{8}{41})\)
\(\frac{1}{2}ln(\frac{25}{41})t = -1.634\)
\(ln(\frac{25}{41})t\)\(= -1.634 * 2\)
\((-0.494)t=-3.268\)
\(t = \frac{-3.268}{-0.494}\)
\(t=6.615\) hours, approximately.
Thus, the chili would reach -10°C at around 6.615 hours.
Hope this helped. This took me a long time.
An AlienWare computer cost $4,200. You have a 35% coupon for their products. How much are you able to purchase the computer for?
Answers
Answer:
$1470 coupon of their product I have
I don’t get this please help me

Answers
Answer:#1: 1225
#2: 1149
Step-by-step explanation:
Hope this helps! :) ❤❤❤
If the terminal side of angle A goes through the point (−24/25,7/25) on the unit circle, then what is sin(A)?
Answers
The value of sin A is, 7/25.
What is Circle?The circle is a closed two dimensional figure , in which the set of all points is equidistance from the center.
We have to given that;
The terminal side of angle A goes through the point (−24/25,7/25) on the unit circle.
Now, By definition we get;
⇒ cos A = - 24/25
⇒ Sin A = 7/25
Thus, The value of sin A is, 7/25.
Learn more about the circle visit:
https://brainly.com/question/24810873
#SPJ1
b. Passes through the point (2, -4) and is parallel to 3x + y = 5
c. Passes through the point (2, -4) and is perpendicular to 3x + y = 5

Answers
keeping in mind that parallel lines have exactly the same slope, let's check for the slope of the equation above
\(3x+y=5\implies y=\stackrel{\stackrel{m}{\downarrow }}{-3}x+5\qquad \impliedby \qquad \begin{array}{|c|ll} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}\)
so we're really looking for the equation of a line that has a slope oif -3 and it passes through (2 , -4)
\((\stackrel{x_1}{2}~,~\stackrel{y_1}{-4})\hspace{10em} \stackrel{slope}{m} ~=~ - 3 \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-4)}=\stackrel{m}{- 3}(x-\stackrel{x_1}{2}) \implies y +4 = - 3 ( x -2) \\\\\\ y+4=-3x+6\implies {\Large \begin{array}{llll} y=-3x+2 \end{array}}\)
now, keeping in mind that perpendicular lines have negative reciprocal slopes
\(\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {\stackrel{slope}{ -3 \implies \cfrac{-3}{1}} ~\hfill \stackrel{reciprocal}{\cfrac{1}{-3}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{1}{-3} \implies \cfrac{1}{ 3 }}}\)
so for this one, we're looking for the equation of a line whose slope is 1/3 and it passes through (2 , -4)
\((\stackrel{x_1}{2}~,~\stackrel{y_1}{-4})\hspace{10em} \stackrel{slope}{m} ~=~ \cfrac{1}{3} \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-4)}=\stackrel{m}{ \cfrac{1}{3}}(x-\stackrel{x_1}{2}) \implies y +4 = \cfrac{1}{3} ( x -2) \\\\\\ y+4=\cfrac{1}{3}x-\cfrac{2}{3}\implies y=\cfrac{1}{3}x-\cfrac{2}{3}-4\implies {\Large \begin{array}{llll} y=\cfrac{1}{3}x-\cfrac{14}{3} \end{array}}\)
Please help me please explain this to me please
Thanks

Answers
Answer:
B- 20
D- no solutions
Step-by-step explanation:
Cuz its light work lol
Answer:
For the first question, the answer is x=20 so the answer is B
For the second I don't know, sorry :(
Step-by-step explanation:
Suppose that a box contains 8 cameras and that 4 of them are defective. A sample of 2 cameras is selected at random. Define the random variable variable x as the number of defective cameras in the sample. What is the probability distribution for x?
Answers
The probability distribution for x is:
x P(x)
0 0.214
1 0.571
2 0.214
How can we determine the probability distribution for x?Since there are 8 cameras in the box, the total number of ways to choose 2 cameras from the box is given by the combination formula:
C(8,2) = 8!/(2!×(8-2)!) = 28
So there are 28 possible ways to choose a sample of 2 cameras.
Now, let's calculate the probability of each possible value of x:
When x = 0, both cameras in the sample are non-defective. The number of ways to choose 2 non-defective cameras from the 4 non-defective cameras in the box is given by the combination formula:
C(4,2) = 4!/(2!×(4-2)!) = 6
So the probability of x = 0 is:
P(x=0) = (number of ways to choose 2 non-defective cameras)/(total number of ways to choose 2 cameras)
= 6/28
= 0.214
When x = 1, one camera in the sample is defective and the other is non-defective. The number of ways to choose 1 defective camera from the 4 defective cameras in the box and 1 non-defective camera from the 4 non-defective cameras in the box is given by the product of the corresponding combinations:
C(4,1) × C(4,1) = 4×4 = 16
So the probability of x = 1 is:
P(x=1) = (number of ways to choose 1 defective camera and 1 non-defective camera)/(total number of ways to choose 2 cameras)
= 16/28
= 0.571
When x = 2, both cameras in the sample are defective. The number of ways to choose 2 defective cameras from the 4 defective cameras in the box is given by the combination formula:
C(4,2) = 4!/(2!×(4-2)!) = 6
So the probability of x = 2 is:
P(x=2) = (number of ways to choose 2 defective cameras)/(total number of ways to choose 2 cameras)
= 6/28
= 0.214
Therefore, the probability distribution for x is:
x P(x)
0 0.214
1 0.571
2 0.214
to know more about probability
brainly.com/question/30034780
#SPJ1
what is the base of 3^x=8
Answers
Answer:
3
Step-by-step explanation:
The equation Y= X^2/2 - 8 and Y= 2X -2 are graphed below what are the solutions to the equation X^2/2 - 8 = 2X -2 
Answers
The equation X^2/2 - 8 = 2X - 2 has two solutions, X = 6 and X = -2. These are the values of X that satisfy the equation and make both equations Y = X^2/2 - 8 and Y = 2X - 2 intersect on the graph.
To find the solutions to the equation X^2/2 - 8 = 2X - 2, we need to set the two equations equal to each other and solve for X.
The equation is:
X^2/2 - 8 = 2X - 2
To simplify the equation, let's multiply both sides by 2 to eliminate the fraction:
X^2 - 16 = 4X - 4
Next, we rearrange the equation to have all terms on one side:
X^2 - 4X - 12 = 0
Now, we can solve this quadratic equation by factoring, completing the square, or using the quadratic formula. Let's use factoring in this case:
(X - 6)(X + 2) = 0
Setting each factor equal to zero gives us two possible solutions:
X - 6 = 0 --> X = 6
X + 2 = 0 --> X = -2
So the solutions to the equation X^2/2 - 8 = 2X - 2 are X = 6 and X = -2.
For more such question on intersect . visit :
https://brainly.com/question/30915785
#SPJ8
The dose of posaconazole in the treatment of oropharyngeal candidiasis is 100 mg twice a day on the first day and then 100 mg once a day for the next 13 days. Posaconazole oral suspension (posaconazole, 40 mg/mL) is available in 4-fluidounce bottles. How many bottles should be dispensed to meet the dosing requirements?
Answers
The number of 4-fluidounce bottles that should be dispensed to meet the dosing requirements for the treatment of oropharyngeal candidiasis is 37.5 bottles.
How is the number of bottles determined?To determine the number of 4-fluidounce bottles, we apply mathematical operations of addition, subtraction, division, and multiplication.
First, the total dosage is determined as 1,500 mg.
Since 40 mg/mL is available in 4-fluidounce bottles, the total dosage is divided by 40 mg/mL to determine the number of bottles required.
Data and Calculations:Dose of posaconazole for the first day = 100 mg twice
= 200 mg (100 mg x 2)
The total number of days for the dosage = 14
Dose for next 13 days = 1,300 mg (100 mg x 13)
Total dosage = 1,500 mg (200 mg + 1,300 mg)
40 mg/mL = 4-fluidounce bottle
1,500 mg = 37.5 bottles (1,500/40)
Thus, the number of 4-fluidounce bottles is 37.5 bottles.
Learn more about mathematical operations at https://brainly.com/question/20628271
#SPJ1