34. Name an error-detection method that can compensate for burst errors
Answers
One error-detection method that can compensate for burst errors is the cyclic redundancy check (CRC).
This method involves adding extra bits to the data being transmitted, which can detect and correct errors in the data. and has error detection. CRC is particularly effective in detecting and correcting burst errors, which occur when a group of consecutive bits are corrupted in a data transmission.
An error-detection method that can compensate for burst errors is the "Reed-Solomon code". Reed-Solomon codes are block-based error correcting codes that can detect and correct multiple errors in data transmissions, making them highly effective in handling burst errors. These codes compensate for burst errors by using redundant information added to the original data, allowing the receiver to accurately reconstruct the original data even in the presence of errors.
Learn more about error-detection here:
https://brainly.com/question/14974469
#SPJ11
Related Questions
need this fast guys .

Answers
Answer:
thanks
Step-by-step explanation:
Answer:
4/3
Step-by-step explanation:
I just used rise/run
a tank is half full of oil that has a density of 900 kg/m3. find the work w (in j) required to pump the oil out of the spout. (use 9.8 m/s2 for g. round your answer to the nearest whole number.) 12 m4 m a spherical tank is given. the tank has radius 12 m and spot coming out of the top with height 4 m.
Answers
To find the work required to pump the oil out of the spout, we need to calculate the potential energy difference between the initial state (when the tank is half full) and the final state (when the tank is empty).
First, let's find the volume of the oil in the tank. Since the tank is half full, the volume of oil is half the volume of the tank. The tank is a sphere with a radius of 12 m, so its volume can be calculated as:
V_tank = (4/3) * π *\(r^3\)
= (4/3) * 3.14159 * \(12^3\)
≈ 7238.23 \(m^3\)
The volume of oil is half of this value:
V_oil = 7238.23 \(m^3\) / 2
≈ 3619.12\(m^3\)
Next, we can calculate the mass of the oil using its density. The density of the oil is given as 900 kg/m^3:
m = density * volume
= 900 kg/\(m^3\) * 3619.12 \(m^3\)
≈ 3257.21 kg
Now, let's calculate the initial and final heights of the oil in the tank.
The initial height is the distance from the center of the tank to the halfway mark, which is half of the tank's radius:
h_initial = r / 2
= 12 m / 2
= 6 m
The final height is zero, as the tank is empty:
h_final = 0 m
Now we can calculate the potential energy difference:
ΔPE = m * g * (h_final - h_initial)
= 3257.21 kg * 9.8 m/\(s^2\) * (0 m - 6 m)
= -190449.528 J
Since work is defined as the negative of the potential energy change:
W = -ΔPE
= -(-190449.528 J)
= 190449.528 J
Rounding to the nearest whole number:
W ≈ 190450 J
Therefore, the work required to pump the oil out of the spout is approximately 190,450 joules.
To know more about potential energy refer here
https://brainly.com/question/24284560#
#SPJ11
how to plot box plot histogram?
Answers
Histograms and box plots are graphical representations for the frequency of numeric data values. The data and explore the central tendency and variability before using advanced statistical analysis techniques.
Histogram:In statistics, a histogram is a graphical representation of the distribution of data. The histogram is represented by a set of rectangles, adjacent to each other, where each bar represent a kind of data. Statistics is a stream of mathematics that is applied in various fields.
Both histograms and box plots are used to explore and present the data in an easy and understandable manner. Histograms are preferred to determine the underlying probability distribution of a data. Box plots on the other hand are more useful when comparing between several data sets. They are less detailed than histograms and take up less space.
To see the image at the bottom of the explanation.
Learn more about Histogram at:
https://brainly.com/question/28975056
#SPJ4

flo and carl each must read a 500-page book. flo reads one page every minute. carl reads one page every 50 seconds. flo starts reading at 1:00, and carl starts reading at 1:30. when will carl catch up to flo? a) using t as the number of minutes after 1:30, set up an equation with the number of pages flo has read on the left side and the number of pages carl has read on the right side. then solve the problem.
Answers
Carl will catch up with Flo after 150 minutes, that is, at 4
To solve this problem, we need to find out when Carl will catch up to Flo in terms of the number of pages read.
Let's first find out how many pages Flo will have read after a certain number of minutes, denoted as 't'. Since Flo reads one page every minute, the number of pages Flo will have read after 't' minutes can be calculated as t.
Next, let's find out how many pages Carl will have read after 't' minutes. Since Carl reads one page every 50 seconds, we need to convert minutes to seconds. There are 60 seconds in a minute, so 50 seconds is equivalent to 50/60 or 5/6 minutes. The number of pages Carl will have read after 't' minutes can be calculated as (5/6)t.
Now, let's set up an equation to represent the situation. We know that Carl starts reading 30 minutes after Flo, so we need to account for this time difference. The number of pages Flo has read after 't' minutes is t, and the number of pages Carl has read after 't' minutes is (5/6)(t + 30).
So, the equation becomes t = (5/6)(t + 30).
To solve this equation, we can multiply both sides by 6 to eliminate the fraction: 6t = 5(t + 30).
Expanding the right side of the equation gives us: 6t = 5t + 150.
Simplifying further, we have t = 150.
Therefore, Carl will catch up to Flo after 150 minutes.
Learn more about the least common multiple: https://brainly.com/question/10749076
#SPJ11
Homework:Section 3. 1
Question 3, 3. 1. 59
Part 1 of 4
HW Score: 60%, 6 of 10 points
Points: 0 of 1
Question content area top
Part 1
Find the inverse function of the function f. Find the range of f and the domain and range of. ;
Question content area bottom
Part 1
Find the inverse, , of f. (x)
enter your response here
(Use integers or fractions for any numbers in the expression
Answers
The inverse function of the given function f is yet to be determined. The range of f and the domain and range of (x) will also be determined.
To find the inverse function of f, we need to swap the roles of x and y in the original function and solve for y. Let's assume the original function f(x) = y. By interchanging x and y, we get x = f^(-1)(y). Now, we can solve this equation to find the inverse function.
Once we find the inverse function f^(-1)(y), we can determine its range. The range of f^(-1) will be the domain of the original function f, and the domain of f^(-1) will be the range of f.
To find the range of f, we need to examine the set of all possible values that y can take on. This can be done by analyzing the behavior of the function and identifying any restrictions or limitations on the output.
Similarly, to determine the domain and range of (x), we need to consider the set of all possible inputs and outputs for the function. The domain of (x) will be the same as the domain of f, and the range of (x) will be the range of f.
In summary, we need to find the inverse function of f by swapping x and y and solving for y. Once we have the inverse function, we can determine its range, which will be the domain of f. Additionally, the domain and range of (x) will be the same as the domain and range of f, respectively.
Learn more about inverse function here
https://brainly.com/question/11735394
#SPJ11
h + 7 < 5 "or" -9h < -45
Answers
Step-by-step explanation:
h+7<5h+7-7<5-7h<-2-9h<-45-9h/-9<-45/-9h<5y - 4= 7(x - 6)
x-intercept
y-intercept
Answers
Answer:
x-intercept: (38/7,0) y-intercept: (0,-38)
Step-by-step explanation:
I think
Jorge builds a rectangular prism that has a volume of 42 cubic inches. Which of the following could be Jorge’s prism? (4 points)
Group of answer choices
A rectangular prism with a height of five inches, length of five inches, and a width of five inches.
A rectangular prism with a height of five inches, length of four inches, and a width of four inches.
A rectangular prism with a height of two inches, length of seven inches, and a width of three inches.
A rectangular prism with a height of six inches, length of three inches, and a width of two inches.
Answers
Answer: A rectangular prism with a height of two inches, length of seven inches, and a width of three inches.
Step-by-step explanation:
Multiply the dimensions given, then select the one that matches Jorge's required 42 in³
5×5×5 = 125
5×4×4 = 80
2×7×3 = 42
6×3×2 = 36
Answer:
A
Step-by-step explanation:
can you guys please help me out I’ll give you a star

Answers
Answer:
{(0,9), (5,8), (-3,7), (-3,2)}
Step-by-step explanation:
Doesn't represent a function because -3 is matched with both 7 and -2
Plzz help me to find coefficient in binomial theorem (25 points)

Answers
Denote x2 by y.
(x2-3)7=(y-3)7
This is a binomial expansion in y, and you want the coefficient of y4 because y4=x8
You have 7 terms of (y-3) in (y-3)7. To get the fourth power of y, you need to choose y from four of the terms. The number of ways you can do this is the combinations of 7 things taken 4 at a time. This is:
7!/(4!3!)=35
So, the coefficient of x8 in the given expansion will be 210.
HOPE IT HELPS
THANK YOU
How many litres can be held by a cylindrical can 14cm in diameter and 20cm hight?
Answers
Answer:
about 3.08 L
Step-by-step explanation:
You want the number of litres in the volume of a cylindrical can 14 cm in diameter and 20 cm high.
LitersA litre is a cubic decimeter, 1000 cubic centimeters. As such, it is convenient to perform the volume calculation using the dimensions in decimeters:
14 cm = 1.4 dm . . . . . . diameter20 cm = 2.0 dm . . . . . heightVolumeThe volume of the cylinder is given by the formula ...
V = (π/4)d²h . . . . . . . where d is the diameter and h is the height
V = (π/4)(1.4 dm)²(2.0 dm) ≈ 3.079 dm³ ≈ 3.08 L
The cylindrical can will hold about 3.08 litres.
<95141404393>

A beam of radiation is to be used to treat a tumor known to be 5.7 cm beneath thepatient's skin. To avoid damaging a vital organ, the radiologist moves the radiationsource over 8.3 cm. At what angle (nearest degree) must the radiologist aim the radiationsource to hit the tumor?

Answers
Explanation:
Let's redraw the diagram first.
To determine the missing angle, we can use the tangent function.
\(\theta=tan^{-1}\frac{opposite\text{ }side\text{ }of\text{ }the\text{ }angle}{adjacent\text{ }side\text{ }of\text{ }the\text{ }angle}\)In the diagram, the opposite side of the angle is the depth of the tumor under the skin surface which is 5.7 cm. The adjacent side of the angle is the horizontal distance on the surface of the skin from the tumor which is 8.3 cm.
Let's plug in these values to the function above.
\(\theta=tan^{-1}\frac{5.7cm}{8.3cm}\)Evaluate the expression using a calculator.
\(\begin{gathered} \theta=tan^{-1}(0.686746988) \\ \theta=34.479\approx34\degree \end{gathered}\)Answer:
Therefore, the radiologist must aim the radiation source at approximately 34º to hit the tumor and avoid damaging the vital organ.

A gardener at a city park bought 1728 bedding plants. Can they be planted in 9 equal rows?
Answers
Answer:
Step-by-step explanation:
Since, the number for each row of bedding plants is unlimited, we can check by dividing them. If it equals a number with no remainder, we can ensure that it can be equally planted!
1728/9=
192
2. There is no remainder so the statement is true!
Answer: Yes they can be planted in 9 equal rows with 192 plants each
JNJ issued 10 year bonds, with a 8% coupon rate, which are paid annually, and currently sell for 992.60, what is the yield to maturity?
Please type your final answer as a positive number, with no comma, and the second decimal place. Write percentage as a whole numbe (ex: 5.34)
Answers
The yield to maturity of the JNJ 10-year bonds is approximately 8.47%.
To calculate the yield to maturity (YTM) of a bond, we need to follow these steps:
1. Calculate the annual interest payment: Multiply the face value of the bond by the coupon rate. In this case, the face value is not given, so we'll assume it is $1,000. Thus, the annual interest payment is $1,000 * 8% = $80.
2. Calculate the number of years until maturity: Since the bond is a 10-year bond, the number of years until maturity is 10.
3. Determine the present value of the bond: We need to find the present value (PV) of the bond by discounting the future cash flows. We are given that the bond currently sells for $992.60, which is the present value.
4. Use the present value formula to calculate the yield to maturity: The formula for calculating the present value of a bond is:
PV = C * (1 - (1 + YTM)^-n) / YTM + F / (1 + YTM)^n
where:
PV = Present value of the bond
C = Annual interest payment (coupon payment)
YTM = Yield to maturity
n = Number of years until maturity
F = Face value of the bond
We know the values for PV, C, and n, and we assume the face value is $1,000. So, we can rearrange the formula to solve for YTM:
YTM = [C * (1 - (PV / F)) / (PV + F)] * (1 / n)
Substituting the given values, we get:
YTM = [80 * (1 - (992.60 / 1000)) / (992.60 + 1000)] * (1 / 10)
Calculating this expression, we find that YTM ≈ 0.0847, or 8.47%.
Therefore, the yield to maturity of the JNJ 10-year bonds is approximately 8.47%.
To know more about the yield to maturity click here:
https://brainly.com/question/33763413
#SPJ11
how many integers from 1 through 1,000 are multiples of 4 or multiples of 6?
Answers
Answer:
375
Step-by-step explanation:
You want to know the number of integers from 1 to 1000 that are multiples of 4 or 6.
MultiplesAssuming the ends of the range are not multiples of interest, we can find the number of multiples of a given number by dividing the range by that number. Doing this for 4, 6, and (4×6), we find that in [1, 1000], there are ...
250 multiples of 4166 multiples of 641 multiples of both 4 and 6The number of multiples of 4 or 6 will be the total of multiples of 4 and multiples of 6, less the number of multiples of both 4 and 6. That is, the first sum counts those multiples of 24 twice.
250 +166 -41 = 375
There are 375 multiples of 4 or 6 in the range 1 to 1000.
<95141404393>

Paul bought a student discount card for the bus. The card allows him to buy daily bus passes for $1.30.
After one month, Paul bought 21 passes and spent a total of $33.30.
Help pls
Answers
Answer:
Paul spent 6 dollars on the student discount card.
Step-by-step explanation:
If each pass is $1.30, simply divide 21 by 1.30
You should get 27.30
Next, subtract 33.30 by 27.30, getting 6.
The mean score for the treatment group is 7.1 (standard deviation of 1.0) and the mean score for control group is 8.4 (standard deviation 2.2). Calculate the effect size to determine the magnitude of the difference between the two groups.
Answers
The effect size (Cohen's d) between the treatment and control groups is approximately -1.91, indicating a large difference.
To determine the effect size and assess the magnitude of the difference between the treatment and control groups, we can use Cohen's d, which is a widely used measure for effect size in statistics. Cohen's d quantifies the standardized difference between means.
Cohen's d is calculated by subtracting the mean score of the control group from the mean score of the treatment group and dividing it by the pooled standard deviation of the two groups. The pooled standard deviation takes into account the variability within each group.
Let's calculate Cohen's d for the given data:
Mean score for treatment group (M1) = 7.1
Standard deviation for treatment group (SD1) = 1.0
Mean score for control group (M2) = 8.4
Standard deviation for control group (SD2) = 2.2
First, we need to calculate the pooled standard deviation (SDp) using the following formula:
SDp = √[(n1-1) * (SD\(1^2\)) + (n2-1) * (SD\(2^2\))] / (n1 + n2 - 2)
where n1 and n2 are the sample sizes for the treatment and control groups, respectively.
Assuming equal sample sizes for simplicity (n1 = n2 = n), we can calculate SDp as follows:
SDp = √[(n-1) * (\(1.0^2\)) + (n-1) * (\(2.2^2\))] / (2n - 2)
= √[1.0^2 +\(2.2^2\)] / 2
= √(1.0 + 4.84) / 2
= √5.84 / 2
≈ √2.92 / 2
≈ 1.36 / 2
≈ 0.68
Now, we can calculate Cohen's d using the following formula:
d = (M1 - M2) / SDp
Substituting the values, we have:
d = (7.1 - 8.4) / 0.68
= -1.3 / 0.68
≈ -1.91
Therefore, the effect size (Cohen's d) is approximately -1.91. The negative sign indicates that the mean score for the treatment group is lower than the mean score for the control group. The absolute value of the effect size (1.91) suggests a large magnitude of difference between the two groups.
It is important to note that effect sizes are interpreted based on the field of study and context. Generally, a Cohen's d of 0.2 is considered a small effect size, 0.5 is moderate, and 0.8 or above is large. In this case, with an effect size of approximately -1.91, the difference between the treatment and control groups can be considered large.
learn more about Effect size.
brainly.com/question/31454248
#SPJ11
Write the slope-intercept form of the equation of the line through the given points.
through: (0, 4) and (1,7)
Answers
Slope = 3
y intercept = 4
========================================================
Explanation:
Let's find the slope.
\(m = \text{slope}\\\\m=\frac{\text{rise}}{\text{run}}\\\\m = \frac{\text{change in y}}{\text{change in x}}\\\\m = \frac{y_2-y_1}{x_2-x_1}\\\\m = \frac{7-4}{1-0}\\\\m = \frac{3}{1}\\\\m = 3\)
The slope is m = 3.
The y intercept is b = 4 due to the point (0,4). The y intercept always occurs when x = 0.
We'll then plug those m and b values into y = mx+b to get the answer y = 3x+4
-----------
As a way to check the answer, plugging x = 0 should lead to y = 4
y = 3x+4
y = 3*0+4
y = 0+4
y = 4
So that works out. Let's try x = 1. It should produce y = 7
y = 3x+4
y = 3*1+4
y = 3+4
y = 7
That works out also. The answer is fully confirmed.
During his hike, Milt drank 1 liter of water and 1 liter of sports drink. How many milliliters of liquid did he drink?
Answers
Answer:
2000 ml of liquid
Step-by-step explanation:
1l plus 1l will equal 2l.
1 liter consists of 1000 milliliters ("milli" means thousand).
If 1l had 1000ml, 2l will have 2000ml.
So 2000mlnis the answer
What would be the 50th term than?
Answers
The 50th term is 290.
What is an arithmetic sequence?It is a sequence where there is a common difference between each consecutive term.
Example:
12, 14, 16, 18, 20 is an arithmetic sequence.
We have,
-4, 2, 8, 14,
This is an arithmetic sequence.
First term = a = - 4
Common difference.
d = 2 - (-4) = 6
d = 8 - 2 = 6
Now,
The nth term = a + (n -1)d
So,
n = 50
a = -4
d = 6
50th term.
= -4 + (50 - 1) 6
= - 4 + 49 x 6
= - 4 + 294
= 290
Thus,
The 50th term is 290.
Learn more about arithmetic sequence here:
https://brainly.com/question/10396151
#SPJ9
The complete question:
What is the 50th term of the sequence that begins −4, 2, 8, 14, ...?
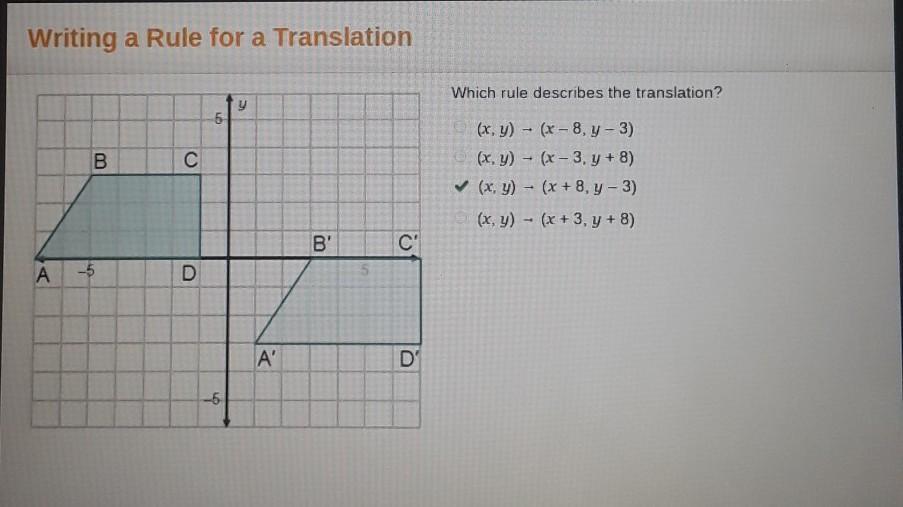
2 trapezoids are shown. Trapezoid 1 has points A (negative 7, 0), B (negative 5, 3), C (negative 1, 3), and D (negative 1, 0). Trapezoid 2 has points A prime (1, negative 3), B prime (3, 0), C prime (7, 0), and D prime (7, negative 3).
Which rule describes the translation?
Answers
Answer:
The answer is C
Step-by-step explanation:
Because I said so
Answer:
C. (x, y) -> (x + 8, y - 3)
Step-by-step explanation:
Hope this helps! :D
Neela is making rectangular place mats that are 12 inches wide and 15 inches long. What is the least amount of ribbon that she will need to create a ribbon border around 1 place mat?
180 inches
54 inches
180 square inches
54 square inches
Answers
Which equation is perpendicular to: y = -6x +2
Select one:
a. y = -6x +3
b.y = 1/6x +5
c. y = 6x +1
d. y = -1/6x +4
Answers
Answer:
b.y=1/6x+1
Step-by-step explanation:
i hopeit will help u
Which relation is a function?
Question 1 options:
{(3,2), (5,8), (3,−4)}
{(−1,6), (−2,7), (−3,6)}
{(5,7), (12,−3), (5,6), (12,7)}
{(3,5),(3,6)}
Answers
Since the others all have 2 same domains with different ranges.
(Please please, actually type the answer and dont send it in a file because it wont work)
A stone pyramid in Egypt has a square base that measures 154 m on each side. The height is 92 m. What is the volume of the pyramid?
Answers
Answer: like 36 i think
Step-by-step explanation:
Answer:
14168
Step-by-step explanation: just multiple
Suppose x(t) = 5sinc(2007). Using properties of the Fourier transform, write down the Fourier transform and sketch the magnitude spectrum, Xo), of i) xi(t) = -4x(t-4), ii) xz(t) = e^{j400}lx(t), iii) X3(t) = 1 - 3x(t) + 1400xlx(t), iv) X(t) = cos(400ft)x(t)
Answers
i) Xi(f) = 5rect(f/2007)e^(-j2πft) | ii) Xz(f) = 5rect((f-400)/2007) | iii) X3(f) = 1 - 3*5rect(f/2007) + 1400(X(f) * X(f)) | iv) X(f) = 5rect(f/5)
Using properties of the Fourier transform, what are the expressions for the Fourier transforms of the following signals: i) xi(t) = -4x(t-4), ii) xz(t) = e^(j400)lx(t), iii) X3(t) = 1 - 3x(t) + 1400xlx(t), iv) X(t) = cos(400ft)x(t)?we'll use properties of the Fourier transform and the given function x(t) = 5sinc(2007).
i) For xi(t) = -4x(t-4):
Using the time shifting property of the Fourier transform, we have:
Xi(f) = X(f)e^(-j2πft)
Since x(t) = 5sinc(2007), the Fourier transform X(f) of x(t) is given by:
X(f) = 5rect(f/2007)
Thus, substituting the values, we have:
Xi(f) = 5rect(f/2007)e^(-j2πft)
ii) For xz(t) = e^(j400)lx(t):
Using the frequency shifting property of the Fourier transform, we have:
Xz(f) = X(f - f0)
Since x(t) = 5sinc(2007), the Fourier transform X(f) of x(t) is given by:
X(f) = 5rect(f/2007)
Substituting the value f0 = 400, we have:
Xz(f) = 5rect((f-400)/2007)
iii) For X3(t) = 1 - 3x(t) + 1400xlx(t):
Using the linearity property of the Fourier transform, we have:
X3(f) = F{1} - 3F{x(t)} + 1400F{x(t)x(t)}
Since x(t) = 5sinc(2007), the Fourier transform X(f) of x(t) is given by:
X(f) = 5rect(f/2007)
Using the Fourier transform properties, we have:
F{x(t)x(t)} = X(f) * X(f)
Substituting the values, we have:
X3(f) = 1 - 3*5rect(f/2007) + 1400(X(f) * X(f))
iv) For X(t) = cos(400ft)x(t):
Using the modulation property of the Fourier transform, we have:
X(f) = (1/2)(X(f - 400f) + X(f + 400f))
Since x(t) = 5sinc(2007), the Fourier transform X(f) of x(t) is given by:
X(f) = 5rect(f/2007)
Substituting the value f = 400f, we have:
X(f) = 5rect((400f)/2007)
Simplifying, we have:
X(f) = 5rect(f/5)
To sketch the magnitude spectrum, Xo(f), we plot the magnitude of the Fourier transform for each case using the given formulas and the properties of the Fourier transform.
Learn more about Fourier transform
brainly.com/question/1542972
#SPJ11
You are trying to decide which of two automobiles to buy. The first is American-made, costs $3.2500 x 104, and travels 25.0 miles/gallon of fuel. The second is European-made, costs $4.7100 x 104, and travels 17.0 km/liter of fuel. If fuel costs $3.50/gallon, and other maintenance costs for the two vehicles are identical, how many miles must each vehicle travel in its lifetime for the total costs (puchase cost + fuel cost) to be equivalent? i||| x 105 miles. eTextbook and Media Hint Assistance Used The total cost of each vehicle is the purchase price plus the fuel price. The fuel price depends upon the fuel efficiency, the miles driven, and the unit fuel cost. Solve simultaneous equations for the miles driven.
Answers
For the total expenditures to be similar, each car must travel 165.79 x 10^3 miles or 1.6579 x 10^5 miles during its lifetime.
The cost of the first automobile is $3.25 x 10^4, and its fuel efficiency is 25.0 miles/gallon of fuel.
The cost of the second automobile is $4.71 x 10^4, and its fuel efficiency is 17.0 km/liter of fuel.
The cost of fuel is $3.50/gallon.
The lifetime of each vehicle requires calculating the number of miles that each automobile must travel for the total cost (purchase cost + fuel cost) to be equivalent.
The total fuel cost of the first vehicle is:
Total Fuel Cost 1 = Fuel Efficiency 1 / Fuel Cost Per Gallon
= 25.0 / 3.50
= 7.1429
The total fuel cost of the second vehicle is:
Total Fuel Cost 2 = Fuel Efficiency 2 * Fuel Cost Per Gallon / Km Per Mile
= 17.0 * 3.50 / 0.621371
= 95.2449
The total cost of the first vehicle for a lifetime of x miles driven is:
Total Cost 1 = Purchase Cost 1 + Fuel Cost 1x
= $3.25 x 10^4 + 7.1429x
The total cost of the second vehicle for a lifetime of x miles driven is:
Total Cost 2 = Purchase Cost 2 + Fuel Cost 2x
= $4.71 x 10^4 + 95.2449x
To find the number of miles each vehicle must travel in its lifetime for the total costs to be equivalent, we need to solve these simultaneous equations by setting them equal to each other:
$3.25 x 10^4 + 7.1429x = $4.71 x 10^4 + 95.2449x
Simplifying the equation:
-$1.46 x 10^4 = 88.102 x - $1.46 x 10^4
Solving for x:
x = 165.79
Therefore, the number of miles that each vehicle must travel in its lifetime for the total costs to be equivalent is 165.79 x 10^3 miles or 1.6579 x 10^5 miles.
Learn more about total expenditures
https://brainly.com/question/31197660
#SPJ11
1 to 7 with the tables and using x to show the value of y

Answers
Answer:
\(12 \times 2\)
89
What is measure of angle 4 measure of angle 5 measure of angle 6? a triangle has angles 1, 2, 3. the exterior angle to angle 1 is 4, to angle 2 is 5, to angle 3 is 6. 180° 270° 300° 360°
Answers
Measure of angle 4 + measure of angle 5 + measure of angle 6 = 360°
The correct answer is an option (d)
Here, the exterior angle to angle 1 is 4.
We can observe that angle 1 and angle 4 are linear angles.
So, ∠1 + ∠4 = 180° .......(1)
Similarly angle 5 is an exterior angle to 5,
⇒ ∠2 + ∠5 = 180° ..............(2)
And the exterior angle to angle 3 is 6.
⇒ ∠3 + ∠5 = 180° ...........(3)
Consider the sum Measure of angle 4 + measure of angle 5 + measure of angle 6:
= m∠4 + m∠5 + m∠6
= 180° - m∠1 + 180° - m∠2 + 180° - m∠3 .....(from (1), (2) and (3))
= 540° - ( m∠1 + m∠2 + m∠3)
= 540° - 180° ........(sum of all angles of triangle is 180°)
= 360°
Therefore, the required sum = 360°
The correct answer is an option (d)
Learn more about triangle here:
https://brainly.com/question/22469440
#SPJ4
The complete question is:
What is Measure of angle 4 + measure of angle 5 + measure of angle 6?A triangle has angles 1, 2, 3. The exterior angle to angle 1 is 4, to angle 2 is 5, to angle 3 is 6.
a) 180°
b) 270°
c) 300°
d) 360°

3a. this table shows the percentage of each food served by a school kitchen. there are 40 weeks in a school year. the school kitchens serve 120kg of food per week. how much food was served in total? 3b. complete the table to show how much of each food type was served. food percentage amount served in a year vegetables 30% potatoes 10% meat 15% rice 35% salad 9% fruit 1%
Answers
The total amount of food served in a year is 4800 kg, and the completed table shows the amounts of each food type served.
3a. To calculate the total amount of food served in a year, we need to multiply the percentage of each food type by the total amount of food served per week (120 kg) and then multiply it by the number of weeks in a school year (40).
Total food served = (Vegetables % * 120 kg/week * 40 weeks) + (Potatoes % * 120 kg/week * 40 weeks) + (Meat % * 120 kg/week * 40 weeks) + (Rice % * 120 kg/week * 40 weeks) + (Salad % * 120 kg/week * 40 weeks) + (Fruit % * 120 kg/week * 40 weeks)
Now let's calculate the total amount of food served using the given percentages:
Total food served = (0.3 * 120 * 40) + (0.1 * 120 * 40) + (0.15 * 120 * 40) + (0.35 * 120 * 40) + (0.09 * 120 * 40) + (0.01 * 120 * 40)
Total food served = 1440 + 480 + 720 + 1680 + 432 + 48
Total food served = 4800 kg
Therefore, a total of 4800 kg of food was served in a year.
3b. To complete the table and show how much of each food type was served, we can multiply the percentage of each food type by the total amount of food served in a year (4800 kg).
Vegetables: 0.3 * 4800 kg = 1440 kg
Potatoes: 0.1 * 4800 kg = 480 kg
Meat: 0.15 * 4800 kg = 720 kg
Rice: 0.35 * 4800 kg = 1680 kg
Salad: 0.09 * 4800 kg = 432 kg
Fruit: 0.01 * 4800 kg = 48 kg
Therefore, the completed table showing the amount of each food type served in a year would be:
Food | Percentage | Amount Served in a Year (kg)
---------------------------------------------------
Vegetables | 30% | 1440
Potatoes | 10% | 480
Meat | 15% | 720
Rice | 35% | 1680
Salad | 9% | 432
Fruit | 1% | 48
To know more about amount visit -
brainly.com/question/18723131
#SPJ11