3) Wages of £4.50 per hour are increased by 8%. Find the new hourly wage.
Answers
-------------------------------------------------------------------------------------------------------------
Answer: \(\textsf{4.86 per hour}\)
-------------------------------------------------------------------------------------------------------------
Given: \(\textsf{Initial wage = 4.50, Increase = 8\%}\)
Find: \(\textsf{New hourly wage}\)
Solution: The first step would be to create an expression to incapsulate the scenario and then we would solve for the new hourly wage and we would get our answer.
Create an expression
\(\textsf{New = Initial * (1 + Increase)}\)\(\textsf{New = 4.50 * (1 + 8\%)}\)\(\textsf{New = 4.50 * (1 + 0.08)}\)Simplify the expression
\(\textsf{New = 4.50 * (1.08)}\)\(\textsf{New = 4.86 hourly wage}\)We were able to determine that the new hourly wage after an increase of 8% would be 4.86 per hour.
Related Questions
Find the area of the figure. If you need to use Pi in your computation, approximate its value as 3.14.
Rectangle topped by a semicircle
a.
130.24 sq. in.
b.
105.12 sq. in.
c.
83.14 sq. in.
d.
180.48 sq. in.

Answers
Answer:
b. 105.12 in²
Step-by-step explanation:
A= 1/2 πr² +ab
a= 8 inb= 10 inr=8/2= 4 inA= 1/2*3.14*4² + 8*10= 105.12 in²what is the median of the following list of 4040 numbers? $$1, 2, 3, ..., 2020, 1^2, 2^2, 3^2, ..., 2020^2$ (a) 1974.5(b) 1975.5(c) 1976.5(d) 1977.5(e) 1978.5
Answers
Median of the following list of 4040 numbers is 1976.5
If we solve 45² = 2025, this value is greater than 2020.
If we solve 44² that would result in 44x44 =1936, this value is less than 2020.
If we subtract 44 from 2020: 2020 - 44 = 1976
There are 1976 of the 4040 numbers that are greater than 2020.
If we add 44 into 2022: 2020 + 44 = 2064
So, there are 2064 numbers which are less than or equal to 2020.
As there are 44 duplicates, it will shift up the median's placement down 44.
List of numbers had been 1, 2, 3, ....,4040
Median of the entire given set would be:
= 1+4040/2
= 2020.5
The median of the following list of 4040 numbers is:
2020.5 - 44= 1976.5
Learn more about median:
https://brainly.com/question/28060453
#SPJ4
consider the infinite geometric series: what is a1? what is r? find the following partial sums: s2
Answers
An infinite geometric series is one in which each term is equal to the preceding term multiplied by a fixed non-zero number, known as the common ratio.
The first term is called a1, and the common ratio is represented by r.In this particular question, we are required to find the value of a1 and r for an infinite geometric series. The partial sum S2 will also need to be found.For a geometric sequence that is infinite, the formula for the partial sum, Sn, is:Sn = a1 / (1-r), where a1 is the first term and r is the common ratio.To solve for a1, it is necessary to know two other variables: the common ratio r and the value of the first term a1. S2 is the sum of the first two terms, so: S2 = a1 + arTo find S2, we must first determine a1 and r. a1 is the first term in the sequence, and r is the common ratio. We can obtain both a1 and r by dividing the second term by the first term.The formula is:r = (ar/a1) = a2/a1 Substitute the value of r and a1 into the formula for S2 to obtain the result: S2 = a1 + ar = a1 + a1r = a1(1+r) Therefore, the value of a1 is a constant number that will appear in the series, and the common ratio, r, will be multiplied by this number to obtain the next value in the series.
So, a1 is the first term, and r is the common ratio of the infinite geometric series. S2, the sum of the first two terms, is found by using the formula S2 = a1 + ar where a1 is the first term and r is the common ratio.
To know more about Geometric series visit-
https://brainly.com/question/30264021
#SPJ11
1.
A 900g tin of chocolate drink powder costs $12.50 and a 1.45kg tin of the
same brand of chocolate drink powder costs $17.90. Which tin gives the
better value for money?
Answers
Answer:
Powder 2
Step-by-step explanation:
Convert to such a way that both quantities are the same:
Powder 1: 1250/9 = 137.7 c
Powder 2: 1790/14.5 = 123.4 c
By doing the above calculation, we have found the cost of 100g , for both powders. Now, compare and find
137.7 > 123.4
But, we're looking for cheapest value, so choose powder 2.
Hope this helps.
The sum of two consecutive even numbers is 214. What are the numbers?
Answers
Step-by-step explanation:
since they are consecutive even numbers, one is bigger by 2 than the other number.
so,
x + (x + 2) = 214
2x + 2 = 214
x + 1 = 107
x = 106
so, the 2 numbers are 106 and 108.
The roundabout at the park has a diameter of 2 meters
A) what is the circumference of the roundabout?
B) what is the area of the roundabout
Answers
Answer:
A) 2π
B) 1π
Step-by-step explanation:
circumference of circle= d×π
circumference=2×π=2π or 6.28 rounded to 2dp
area of circle= r^2×π
radius=2÷2=1
radius=1^2×π
radius=1π or 3.14 rounded to 2dp
A) The circumference of a circle can be found by multiplying its diameter by pi (π). Therefore, the circumference of the roundabout is:
Circumference = 2 x π x radius
Radius = diameter/2 = 2/2 = 1 meter
Circumference = 2 x π x 1 = 2π meters
B) The area of a circle can be found by multiplying its radius squared by pi (π). Therefore, the area of the roundabout is:
Area = π x radius^2
Area = π x 1^2 = π square meters or approximately 3.14 square meters.
Solve the compound inequality and graph the solutions.1

Answers
A compound inequality is formed by two inequalities, with diferent values ≤≥<>
Then first divide the inequality in
1≤ x + 7
and
x + 7< 5
then first becomes
-x ≤ 7-1≤6 or same x≥ -6
second inequality becomes
x < 5-7 < -2
then the composed inequality solution is
-6 ≤ x < -2

1) If f(x) = 6x, find f(2).
Answers
Use a triple integral to find the volume of the solid enclosed by the paraboloids y = x^2 + z^2 and y = 32 - x^2 - z^2
Answers
The volume of the solid enclosed by the two paraboloids is approximately 1365.34π cubic units.
Here, we have to find the volume of the solid enclosed by the two paraboloids \(y = x^2 + z^2\) and \(y = 32 - x^2 - z^2\),
we need to set up a triple integral in cylindrical coordinates.
In cylindrical coordinates, we have:
x = r cos(θ)
z = r sin(θ)
y = y
The limits of integration for r, θ, and y will depend on the region of integration.
First, let's find the intersection points of the two paraboloids:
\(x^2 + z^2 = 32 - x^2 - z^2\\2x^2 + 2z^2 = 32\\x^2 + z^2 = 16\)
This represents a circular region with radius r = 4 in the x-z plane.
Now, let's find the limits of integration for r, θ, and y:
For r:
Since the circular region has a radius of 4, the limits of r will be from 0 to 4.
0 ≤ r ≤ 4
For θ:
The intersection points form a complete circle in the x-z plane, so the limits of θ will be from 0 to 2π.
0 ≤ θ ≤ 2π
For y:
The lower paraboloid is given by \(y = x^2 + z^2\), and the upper paraboloid is given by \(y = 32 - x^2 - z^2\).
The limits of y will be from the lower paraboloid to the upper paraboloid.
\(x^2 + z^2 \leq y \leq 32 - x^2 - z^2\)
Now, we can set up the triple integral to find the volume V:
V = ∫∫∫ (y) dy dθ dr
V = ∫∫∫ \((r^2 cos^2(\theta) + r^2 sin^2(\theta)) dy d\theta dr\)
V = ∫∫∫ \((r^2) dy d\theta dr\)
V = ∫∫ \((r^2) y|_{(x^2+z^2)}^{(32-x^2-z^2)} d\theta dr\)
V = ∫∫ \((r^2) (32 - 2x^2 - 2z^2) d\theta dr\)
V = ∫ \((32r^2 - 2r^2(x^2 + z^2)) d\theta dr\)
V = ∫ \((32r^2 - 2r^2r^2) d\theta dr\)
V = ∫ \((32r^2 - 2r^4) d\theta dr\)
Now, integrate with respect to θ from 0 to 2π:
V = ∫(0 to 2π) ∫(0 to 4) \((32r^2 - 2r^4)\) dr dθ
Now, integrate with respect to r from 0 to 4:
V = ∫(0 to 2π) \([(32/3)r^3 - (1/3)r^5] |_0 ^4\) dθ
V = ∫(0 to 2π) \([(32/3)(4^3) - (1/3)(4^5)]\) dθ
V = ∫(0 to 2π) [(32/3)(64) - (1/3)(1024)] dθ
V = ∫(0 to 2π) [682.67] dθ
V = 682.67 * (2π) - 682.67 * (0)
V = 1365.34π cubic units
Therefore, the volume of the solid enclosed by the two paraboloids is approximately 1365.34π cubic units.
To know more about Paraboloids visit:
brainly.com/question/14307074
#SPJ12
Find the distance of D of AB
A=(-7,-7) B= (-3,-1)

Answers
The distance between the points A=(-7,-7) and B=(-3,-1) is 7.21 units.
Finding the distance of D of ABWe can use the distance formula to find the distance between points A=(-7,-7) and B=(-3,-1) on the coordinate plane.
The distance formula is:
d = √((x2 - x1)^2 + (y2 - y1)^2)
where (x1, y1) and (x2, y2) are the coordinates of the two points.
Substituting the values we have, we get:
d = √((-3 - (-7))^2 + (-1 - (-7))^2)
= √((4)^2 + (6)^2)
= √(16 + 36)
= √(52)
≈ 7.21
Therefore, the distance between points A=(-7,-7) and B=(-3,-1) is approximately 7.21 units.
Read more about distance at
https://brainly.com/question/28551043
#SPJ1
Hikes a location 27 meters above sea level. Brain hikes to a location 21 meters below sea level. Write an integer yo represent each hiker location with respect to sea level
Answers
Answer:
The number describing its location of Melissa to the sea-level is= 27
The number which would be the position of Brian to the sea-level is = -21
Step-by-step explanation:
The number may be negative, positive, or zero.
Let the sea level be 0.
They realize that the location of Melissa is 27 meters and above the sea-level, per the relevant information given throughout the exercise.
It also may assume that it's numerical representing its position becomes greater than zero throughout terms of sea-level (this means that it is positive).
It would then be= 27
The place of Brian is 21 m away from the sea.
The integer of its location is less than zero (negative), as regards the amount of the sea.
It is, therefore= -21
Find U infinity i = 1 Ai and infinity i = 1 Ai if for every positive integer i, Ai = {i, i + 1, i + 2 ,...}. Ai = {0, i}. Ai = (0, i), that is, the set of real numbers x with 0 < x < i. Ai = (i, infinity), that is, the set of real numbers x with x > i.
Answers
We can use the formula for the sum of an arithmetic series to find the value of U infinity i = 1 Ai for each given set Ai:
(a) Ai = {i, i + 1, i + 2,...}
The sum of this arithmetic series is:
U infinity i = i + (i + 1) + (i + 2) + ...
= i + (i + 1) + (i + 2) + ... + (i + n) - (1 + 2 + 3 + ... + n)
where n is any positive integer.
The sum of the first n positive integers is given by the formula:
1 + 2 + 3 + ... + n = n(n+1)/2
Substituting this into the expression for U infinity i, we get:
U infinity i = i + (i + 1) + (i + 2) + ... + (i + n) - n(n+1)/2
Simplifying, we get:
U infinity i = (n+1)i + n(n+1)/2 - n(n+1)/2
= (n+1)i
Taking the limit as n approaches infinity, we get:
U infinity i = lim (n approaches infinity) (n+1)i = infinity
Therefore, U infinity i = 1 Ai for the set Ai = {i, i + 1, i + 2,...} is infinity.
(b) Ai = {0, i}
The sum of this arithmetic series is:
U infinity i = 0 + 1 + 2 + ... + i-1 + i
Using the formula for the sum of an arithmetic series, we get:
U infinity i = [i(i+1)]/2
Taking the limit as i approaches infinity, we get:
U infinity i = lim (i approaches infinity) [i(i+1)]/2 = infinity
Therefore, U infinity i = 1 Ai for the set Ai = {0, i} is infinity.
(c) Ai = (0, i)
The sum of this set is:
U infinity i = integral from 0 to i dx
Evaluating the integral, we get:
U infinity i = [x] from 0 to i = i
Therefore, U infinity i = 1 Ai for the set Ai = (0, i) is i.
(d) Ai = (i, infinity)
The sum of this set is:
U infinity i = integral from i to infinity dx
Taking the limit as the upper limit of integration approaches infinity, we get:
U infinity i = lim (b approaches infinity) integral from i to b dx
= lim (b approaches infinity) (b - i)
= infinity
Therefore, U infinity i = 1 Ai for the set Ai = (i, infinity) is infinity.
To know more about U infinity i refer here:
https://brainly.com/question/133621833#
#SPJ11
i will give brainliest to whoever answers correctly. this is due in 10 minutes so i would appreciate if you could do it

Answers
Answer:
choice 1) 7
Step-by-step explanation:
6 + (9-1)^2 / 4 x (1/2)^4
6 + 64/4(1/16)
6+16/16
6+1 = 7
HELP PLEAASE i need answer nowwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwww

Answers
Answer:Irrational,2/9,22/100 11/50, Irrational, No Fraction Given, Perfect Square, Non-Perfect Square
Step-by-step explanation:Best fit options for each question.
X + 2x - 7/4=1 - x/2 -x ayudaaaaa
Answers
Answer:
|x| - |-x| = 0
Step-by-step explanation:
Answer:
no se
Step-by-step explanation:
no se
It takes Imani seven hours to dig a 10 ft by 10 ft hole. Stefan can dig the same hole in five hours. If they worked together how long would it take them
Answers
Answer:
2 hours and 44 min. or 2.7273 hours
Step-by-step explanation:
Ryan: 1 hole per 5 hours
Castel: 1 hole per 6 hours
x = time if working together then
x(1/5 + 1/6) = 1
x(6 + 5) = 30
11x = 30
x = 30/11
x = 2.7273 hours
or
x = 2 hours and 44 minutes
Chang knows one side of a triangle is 13 cm. Which set of two sides iS possible for the lengths of the other two sides
of this triangle?
O 5 cm and 8 cm
• 6 cm and 7 cm 7
O 7 cm and 2 cm
• 8 cm and 9 cm
Answers
Answer:
8 cm and 9 cm by using a>b+c where a, b and c are sides of a triangle
y is inversely proportional to x.
When x=9, y = 8.
Find y when x= 6.
Answers
Answer:
y = 12 when x = 6
Step-by-step explanation:
The equation for inverse proportion is
xy = k where k is a constant
Let x = 9 and y = 8
9*8 = k
72 = k
The equation is xy = 72
Let x=6
6*y = 72
Divide each side by 6
6y/6 = 72/6
y =12
Two hikers, Alan and Ben, are 12.6 miles apart and walking towards each other. They meet in 3 hours. Find the rate of each hiker if Ben walks 0.8 mph faster than Alan.
Alan's rate of speed is _____ mph. (Round to one decimal place.)
Ben's rate of speed is ___ mph. (Round to one decimal place.)
Answers
In response to the supplied query, we may state that Ben's speed, equation rounded to one decimal place, is x + 0.8 = 2.5 mph.
What is equation?Using the equals symbol (=) to indicate equivalence, a math equation links two statements. Algebraic equations prove the equality of two mathematical expressions by a mathematical assertion. The equal sign, for example, provides a gap between the numbers 3x + 5 and 14 in the equation 3x + 5 = 14. You can use a mathematical formula to understand the connection between the two phrases that are written on opposite sides of a letter. Most of the time, the logo and the particular software match. e.g., 2x - 4 = 2 is an example.
Rate times distance
Let x represent Alan's speed in mph. Ben's speed will then be x + 0.8 mph.
They will have travelled 12.6 kilometres in total when they finally cross paths. The formula is as follows:
\(12.6 = (x + x + 0.8) × 3\\12.6 = 6x + 2.4 \s10.2 = 6x \sx = 1.7\)
Alan is moving at a speed of 1.7 mph, decimal place included.
Ben's speed, rounded to one decimal place, is x + 0.8 = 2.5 mph.
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
Answer:
Alan's rate of speed is 1.7 mph.
Ben's rate of speed is 2.5 mph.
Step-by-step explanation:
We can use the distance-rate-time formula to solve the given problem.
\(\boxed{\sf Distance=rate \times time}\)
Create a distance equation for each of the hikers.
AlanDistance = dSpeed = rTime = 3 hoursTherefore, the equation for Alan's distance in terms of r is:
\(\implies \sf d = 3r\)
BenDistance = dSpeed = r + 0.8 (as Ben walks 0.8 mph faster than Alan)Time = 3 hoursTherefore, the equation for Ben's distance in terms of r is:
\(\implies \sf d = 3(r+0.8)\)
Alan and Ben are 12.6 miles apart and walking toward each other.
Therefore, their combined distances will equal 12.6 miles.
Set the sum of the found expressions for distance equal to 12.6 and solve for r:
\(\implies \sf d_{Alan}+d_{Ben}=12.6\)
\(\implies \sf 3r+3(r+0.8)=12.6\)
\(\implies \sf 3r+3r+2.4=12.6\)
\(\implies \sf 6r+2.4=12.6\)
\(\implies \sf 6r=10.2\)
\(\implies \sf r=1.7\)
Therefore:
Ben = r = 1.7 mphAlan = r + 0.8 = 1.7 + 0.8 = 2.5 mphSolutionAlan's rate of speed is 1.7 mph.
Ben's rate of speed is 2.5 mph.
Which equation is true?
104 = 1,000
105 = 10 × 1,000
106 = 10,000 × 100
107 = 1,000,000
Answers
The true equation is 10^6 = 10,000 × 100
The expressions are expressed to the power of 10 :
10^4 = 10 × 10 × 10 × 10 = 10000
10^5 = 10 × 10 × 10 × 10 × 10 = 100,000
10^6 = 10 × 10 × 10 × 10 × 10 × 10 = 10,000 × 100 = 1,000,000 (total of 6 zeros)
10^7 = 10 × 10 × 10 × 10 × 10 × 10 × 10 = 10,000,000
Hence, the only true equation is 10,000 × 100
Learn more : https://brainly.com/question/6109146?referrer=searchResults
What are all the possible first steps in factoring a polynomial with four terms?
Answers
The first step to factorizing a polynomial is taking the Highest Common Factors.
Polynomials:Like Algebraic expressions, polynomials are expressions that consist of both coefficients and variables are called Polynomials.
Factoring a Polynomial:The factors that are multiplied to obtain the original expressions are known as factors of the given polynomial.
Factorization is the method used to determine the factors of a given polynomial or mathematical expression.
To factorize a given polynomial first we need to take the Highest common factors from the 4 terms of the polynomial.
Example:
x²-5x -10x +50
To factorize the polynomial
Take common Highest Common Factors
=> x(x - 5) -10(x - 5)
=> (x - 5) (x - 10)
∴ Factors of given polynomial is (x - 5) and (x - 10)
Therefore,
The first step to factorizing a polynomial is taking the Highest Common Factors.
Learn more about Factoring a Polynomial at
https://brainly.com/question/28315959
#SPJ4
Name
Chapter
5
1.On a calendar, each day is represented by a rectangle. To keep track of the date, you cross off the
previous day by connecting one pair of opposite corners of the rectangle, as shown.
10
E 177
11
F18
12
b. List the five triangle congruence theorems.
G10
a. Classify AABE by its sides and by measuring its angles. Explain your reasoning.
D
Date
c.For each of the triangle congruence theorems you listed in part (b), prove that AFBC = ACGF
using that theorem. (You will need to write five different proofs.)
Answers
The triangle theorems will be:
Side-Side-Side (SSS) Congruence Theorem:Side-Angle-Side (SAS) Congruence Theorem:Angle-Side-Angle (ASA) Congruence Theorem:Hypotenuse-Leg (HL) Congruence Theorem:Angle-Angle-Side (AAS) Congruence TheoremHow to explain the theoremSide-Side-Side (SSS) Congruence Theorem: If the three sides of one triangle are congruent to the three sides of another triangle, then the two triangles are congruent.
Side-Angle-Side (SAS) Congruence Theorem: If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.
Angle-Side-Angle (ASA) Congruence Theorem: If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
Angle-Angle-Side (AAS) Congruence Theorem: If two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, then the two triangles are congruent.
Hypotenuse-Leg (HL) Congruence Theorem: If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another right triangle, then the two triangles are congruent.
Learn more about theorem on
https://brainly.com/question/17335144
#SPJ1
2x+54/x where x=9
what is the answer?
Answers
inductive or deductive all numbers divisible by 6 are also divisible by 3. 36 is divisible by 6. so, 36 is divisible by 3.
Answers
Answer:
deductive
Step-by-step explanation:
A supply company manufactures copy machines. The unit cost C (the cost in dollars to make each copy machine) depends on the number of machines made. If x machines are made in the unit cost is given by the function C(x)=x^2-520x+79,797. What is the minimum unit cost? Do not round your answer.
Answers
Answer:
The minimum unit cost is $12,197.
Explanation:
The cost function is given below:
\(C\mleft(x\mright)=x^2-520x+79,797\)To find the minimum unit cost, first, find the derivative of C(x).
\(C^{\prime}(x)=2x-520\)Next, set the derivative equal to 0 and solve for x.
\(\begin{gathered} 2x-520=0 \\ 2x=520 \\ x=520\div2 \\ x=260 \end{gathered}\)Finally, substitute x=260 into C(x) to find the minimum cost.
\(\begin{gathered} C\mleft(x\mright)=x^2-520x+79,797 \\ \implies C(260)=(260)^2-520(260)+79,797 \\ =67600-135,200+79,797 \\ =12,197 \end{gathered}\)The minimum unit cost is $12,197.
an experimenter measures the weights of 5 mice, with the following weights in grams: 56, 59, 78, 56, 77. what is the standard deviation of the sample?
Answers
The value of standard deviation of the sample is 11.29 grams.
To calculate the standard deviation of a sample, we need to use the following formula:
s = sqrt [ Σ(xi - x)^2 / (n-1) ]
where s is the standard deviation of the sample, Σ(xi - x)^2 is the sum of the squared deviations of each data point from the sample mean, n is the sample size and x is the sample mean
To calculate the standard deviation for the weights of the 5 mice, we first need to find the sample mean:
x = (56 + 59 + 78 + 56 + 77) / 5 = 65.2
Next, we can calculate the sum of the squared deviations:
Σ(xi - x)^2 = (56 - 65.2)^2 + (59 - 65.2)^2 + (78 - 65.2)^2 + (56 - 65.2)^2 + (77 - 65.2)^2
= 82.36 + 41.64 + 156.64 + 82.36 + 147.56
= 510.56
Finally, we can calculate the standard deviation:
s = sqrt [ Σ(xi - x)^2 / (n-1) ] = sqrt [ 510.56 / (5-1) ] = sqrt [ 127.64 ] = 11.29
Therefore, the standard deviation is 11.29 grams.
To know more about standard deviation:
https://brainly.com/question/23907081
#SPJ4
Find points on the ellipse x^2/9 y^2 closest to (2,0)
Answers
the points on the ellipse that are closest to the point (2,0) are (2, sqrt(5/9)) and (2, -sqrt(5/9)).
To find the points on the ellipse x^2/9 + y^2 = 1 that are closest to the point (2,0), we can use the method of Lagrange multipliers. We want to minimize the distance between the point (2,0) and a point (x,y) on the ellipse, subject to the constraint that the point (x,y) satisfies the equation of the ellipse. Therefore, we need to minimize the function:
f(x,y) = sqrt((x-2)^2 + y^2)
subject to the constraint:
g(x,y) = x^2/9 + y^2 - 1 = 0
The Lagrange function is:
L(x,y,λ) = sqrt((x-2)^2 + y^2) + λ(x^2/9 + y^2 - 1)
Taking the partial derivatives of L with respect to x, y, and λ, and setting them equal to zero, we get:
∂L/∂x = (x-2)/sqrt((x-2)^2 + y^2) + (2/9)λx = 0
∂L/∂y = y/sqrt((x-2)^2 + y^2) + 2λy = 0
∂L/∂λ = x^2/9 + y^2 - 1 = 0
Multiplying the first equation by x and the second equation by y, and using the third equation to eliminate x^2/9, we get:
x^2/9 + y^2 = 2xλ/9
x^2/9 + y^2 = -2yλ
Solving for λ in the second equation and substituting into the first equation, we get:
x^2/9 + y^2 = -2xy^2/2x
Multiplying both sides by 9x^2, we get:
9x^4 - 36x^2y^2 + 36x^2 = 0
Dividing by 9x^2, we get:
x^2 - 4y^2 + 4 = 0
This is the equation of an ellipse centered at (0,0), with semi-axes of length 2 and 1. Therefore, the points on the ellipse x^2/9 + y^2 = 1 that are closest to the point (2,0) are the points of intersection between the ellipse and the line x = 2.
Substituting x = 2 into the equation of the ellipse, we get:
4/9 + y^2 = 1
Solving for y, we get:
y = ±sqrt(5/9)
To learn more about ellipse visit:
brainly.com/question/19507943
#SPJ11
I need help I don't understand this.
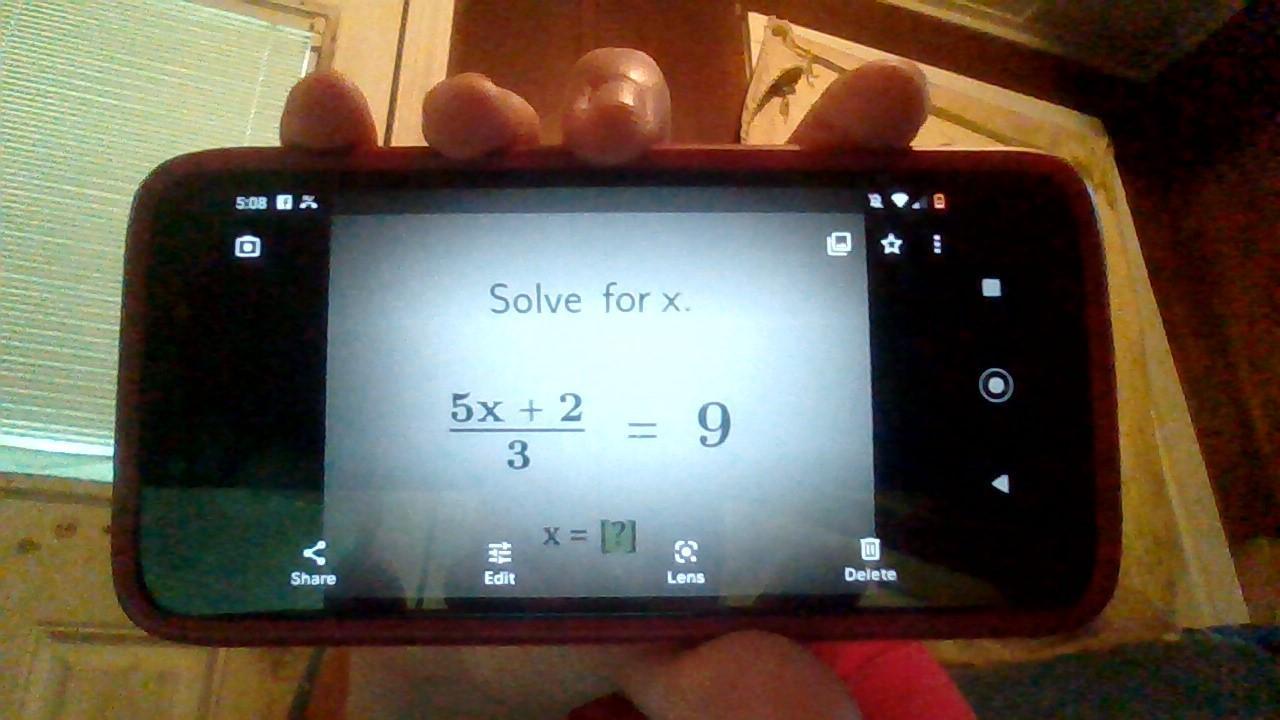
Answers
Answer:
x=5
Step-by-step explanation:
(5x+2)/3 = 9
Multiply each side by 3
(5x+2)/3 *3 = 9*3
5x+2 = 27
Subtract 2 from each side
5x+2-2 = 27-2
5x = 25
Divide by 5
5x/5 = 25/5
x =
bob and carol do a job together in 2 hours. bob can do the job in 6 hours by himself. how long would it take carol by herself? group of answer choices
Answers
Carol can do the same work in 3 hours as it is did by bob
What is Arithmetic equation?
The area of mathematics known as arithmetic deals with the study of numbers and the numerous operations that can be performed on them.
Addition, subtraction, multiplication, and division are the fundamental mathematical operations.
The process of adding two or more numbers together is called addition.The method of subtraction is used to take things out of the initial group.Multiplication is the process of repeatedly adding the same integer.An object or group is divided into smaller pieces or groups when it is large. .bob + carol = 2 hours
bob = 6 hours
L.C.M of both equation is 6
∴efficiency of bob + carol is 3
∴efficiency bob is 1
Then, 3 - 1 = 2
total work ÷ 2
6 ÷ 2 = 3
To know more about arithmetic, please visit:
https://brainly.com/question/11424589
#SPJ4
A train leaves Chicago at 6:00 AM, another train leaves Philadelphia at 6:00 AM. Which train will leave first?
Answers
Answer:
Step-by-step explanation:
6:00 a.m. in Philadelphia comes 1 hour before 6:00 a.m. in Chicago, so it is the Philadelphia train that leaves first.